Introduction
Currently the most prevalent start-up technique of Steam Assisted Gravity Drainage (SAGD) is the Steam Cycle Start-up, which has flaws such as high heat loss along the route and large consumption of steam. Moreover, reservoir heterogeneity can have a severe negative impact on the start- up quality[1]. Electric heating of the reservoir can remedy the defects above. Since no steam is injected into the reservoir, on the one hand, heating profile can be more uniform with less interference from heterogeneity; on the other hand, substantial heat loss along the pipe is avoided, conserving considerable energy and water[2]. Meanwhile, simple and compact, equipment used in electric heating can be installed and controlled easily and can save surface operating space and considerable amount of maintenance fee, which renders the electric heating a thermal recovery technique with broad prospect[3].
With respect to SAGD start-up by electric heating, several quantitative studies have been conducted. Moini, et al.[4] established a model for calculation of energy consumption of electric heating in SAGD start-up in 2013, but the model has some limitations: (1) Underground temperature distribution during the start-up cannot be determined; (2) As a single-well model, it doesn’t consider the interference of multiple wells; (3) Energy, water and fuel conservation of electric heating aren’t quantified in the model. A model for SAGD electrical preheating process was advanced by Wei et al. in 2016[5], subsequently a finite element numerical model was proposed by Medizade et al. in 2017[6], both of which are dedicated to tackle the temperature distribution and energy consumption, but are solely applicable to control pattern based on constant-power per unit length (W/m). With the rapid development of this technique, the control pattern of electrical heating can be switched between the constant-power heating and constant-temperature heating flexibly. Compared with the traditional constant-power heating, constant-temperature heating has many advantages, such as intuitive control of heating temperature and effective prevention of crude coking near the wellbore[7,8]. Additionally, under certain circumstances, it is possible to lower the energy consumption by constant-temperature heating mode. Hence, how to predict the key indexes under constant-temperature heating is an urgent issue of great significance waiting to be answered.
A mathematic model for constant-temperature electric heating of dual-horizontal-well SAGD start-up is proposed in this study and it can be used to calculate the underground temperature distribution and energy-consumption parameters during SAGD. Moreover, methods to calculate the energy, water and fuel saved by electric heating than steam heating are set up. With the terminal start-up temperature given, the model can also predict the time and energy consumption of the whole start-up process.
1. Principle of constant-temperature heating
The constant-temperature heating is mainly actualized by feedback adjustment mechanism (Fig. 1). During field operation, thermocouples are installed inside the wellbore to monitor the temperature of the heating cable, and the temperature signals collected are transmitted to the surface Proportion-Integrals-Differential (PID) controller where feedback adjustment is performed. In this system, the measured temperature and designed temperature are compared in real time by the central chip to narrow the deviation between the two. When the measured temperature is lower than the designed one, the central chip delivers an instruction of keeping on heating. When the actual temperature exceeds the designed temperature, then the central chip sends out an instruction to suspend heating and the temperature begins to drop as a result. Eventually a dynamic equilibrium between the state of operation and suspension of the heating system can be reached during which the actual temperature of the heater fluctuates within a tiny range. Meanwhile, via the PID and repeaters, the temperature measured in real-time is transmitted to the Remote Control Center where the data is saved and analyzed, realizing dynamic monitoring of the data[9].
Fig. 1.
Diagram of the intelligent control of the constant-temperature electric heating in start-up of dual-horizontal-well SAGD.
2. Mathematical model for constant-temperature electric heating mode
2.1. Basic assumptions for the proposed model
Basic assumptions for the proposed model are: (1) Hori-zontal sections of the well pair are mutually parallel. (2) Formation is homogeneous and even in thickness with constant properties such as thermal conductivity and heat capacity. (3) During the preheating process, the thermal parameters of the oil layer (such as heat conductivity and thermal diffusivity etc) don’t change with temperature. (4) Reservoir fluid doesn’t migrate and thus the gravity action can be ignored. (5) No thermal convection happens in the formation. (6) Energy loss between the heater and wellbore is quantified by electricity-heat conversion & transmission efficiency.
2.2. Cylindrical plane source solutions for constant- temperature electric heating in infinite reservoirs
The differential equation in a radial coordinate system denoting the heat conduction where constant-temperature electric heating is implemented via a horizontal wellbore in an infinite homogeneous cylindrical reservoir is:
In order to boost the general applicability of the solution, dimensionless treatment is applied to critical variables. The temperature increment is nondimensionalized as below:
The time is nondimensionalized as below:
The distance is nondimensionalized as below:
After nondimensionlization equation (1) can be converted to:
The initial condition is:
The internal boundary condition is:
The external boundary condition is:
The Laplace transform is defined to the dimensionless time ${{t}_{D}}$ as below:
Apply Laplace transform to equation (5) and the dimensionless temperature increment in Laplace domain can be obtained:
Then temperature distribution in the formation at any given moment is:
2.3. Quantification of energy consumption during constant-temperature electric heating
Under the traditional constant-power electric heating mode, cumulative energy consumption can be calculated by simple product operation. Whereas when it comes to the constant-temperature electric heating mode, real-time power varies with time, thus cumulative energy consumption cannot be worked out by any simple operation, which is more difficult and needs further deliberation below.
According to the Fourier law, heat flux in the formation is:
Then heat flux of the wellbore can be expressed as:
Integrate the equation (14) to calculate the real-time thermal power consumed by the reservoir:
Real-time electric power consumed at surface is:
Cumulative thermal energy consumed by the formation is:
Apply Laplace transform to equation (17):
Apply Laplace inverse transform to equation (18):
Then the cumulative electric energy consumed at surface can be calculated by:
2.4. Disposition of multi-well interference based on superposition principle
Since there are two horizontal wells in a dual-well SAGD unit, forming a well pair, there is interference between them. In line with the linear feature of the heat conduction equation, superposition principle is applicable to solve the question of temperature distribution in which multiple wells heat at the same time, the temperature increment for any point in the formation at any given time equal to the algebraic sum of temperature increment induced by each well working alone. Then from the equation (12), it can be attained:
If the wells are the same in heating temperature and duration, then equation (21) can be simplified as:
Similarly, the thermal power consumed by the formation under multiwell circumstance can be obtained:
The electric power consumed on the surface under multiwell circumstance is:
From the equation (19), the cumulative thermal energy consumed by the formation under multiwell circumstance is:
From the equation (20), the cumulative electric energy consumed on the surface under multiwell circumstance is:
If the length of heated section, heating temperature and duration, transmission efficiency of surface electric energy, electricity-heat conversion & transmission efficiency of all the wellbore heater are equal, then equation (24) can be simplified as:
If the radius of the wellbores are equal, then equation (26) can be simplified as:
For the dual-horizontal-well SAGD, m=2.
2.5. Calculation of energy, water and fuel saved
In an electric-heating block the relationship between transmission efficiency of electricity and loss rate of electricity is:
For each heater inside a wellbore, the relationship between the electricity-heat conversion & transmission efficiency and loss rate of electricity during transmission is:
If the cumulative thermal energy consumed in the formation is Qf , then the cumulative electric energy consumed on surface by electric heating is:
In a steam-heating block, the relationship between transmission efficiency of steam and heat loss rate of steam is:
Since what steam carries is thermal energy, there is no issue of energy conversion in the formation. If the cumulative thermal energy consumed in the formation is Qf , then cumulative thermal energy consumed on surface by steam heating is:
From the equation (31) and equation (33), surface energy consumption saved by electric heating than steam heating under the same formation cumulative energy consumption can be calculated by:
The percentage of energy consumption saved on surface by electric heating than steam heating is:
It is the latent heat of vaporization that is converted into thermal energy injecting underground during steam heating. If the cumulative surface energy consumption is Qg , then the thermal energy demanded to be injected into the formation is Qf , and the cumulative water consumption equivalent is:
Since no water is consumed during the electric heating process, mw is just the water consumption equivalent saved by electric heating than steam heating.
Fuel oil or gas is often used as fuel for furnace in the steam heating process. If the cumulative surface energy consumption in steam heating is Qg (equivalent to inject thermal energy Qf into the oil layer) , then the fuel oil consumed at surface is:
Or the volume of fuel gas (in standard condition) consumed at surface is:
Since no fuel is consumed during the electric heating process, mo or Vg is just the fuel oil or gas consumption equivalent saved by electric heating than steam heating.
3. Model verification
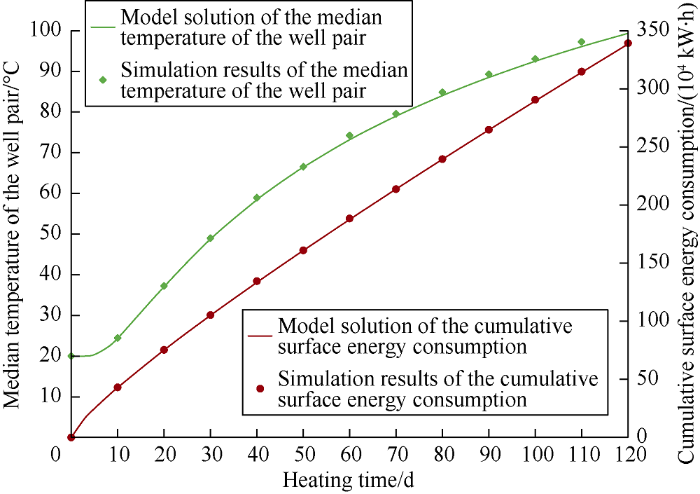
To verify the proposed model, a typical SAGD well pair from the Fengcheng Oilfield in Xinjiang, China was selected, named Well-pair A, its median temperature and cumulative surface energy consumption were calculated by both the established model and commercial simulator of COMSOL Multiphysics, and the calculated results were compared to verify the accuracy and reliability of the proposed model.
Parameters of Well-pair A are listed as Table 1. The thermophysical parameters of the formation are weighted mean by volume proportion of properties of rock, oil and formation water. Heating condition was set at constant-temperature heating of 240 °C for 120 d.
Table 1 Basic data of Well-Pair A in a developing block of dual-horizontal-well SAGD in Fengcheng Oilfield, Xinjiang, China.
| Name of the parameter | Value of the parameter | Name of the parameter | Value of the parameter |
|---|---|---|---|
| Porosity | 30% | Thermal conductivity of rock | 2.38 W/(m•K) |
| Density of formation water | 1 000 kg/m3 | Specific heat capacity of formation water | 4 200 J/(kg•K) |
| Oil saturation | 85% | Thermal conductivity of formation water | 0.58 W/(m•K) |
| Horizontal section length of a single well | 800 m | Density of crude | 965 kg/m3 |
| Density of rock | 1 750 kg/m3 | Wellbore radius | 0.088 9 m |
| Distance between two horizontal wells in a well pair | 5 m | Initial temperature of the reservoir | 20 °C |
| Specific heat capacity of crude | 2 469 J/(kg•K) | Thermal diffusivity | 8.02×10-7 m2/s |
| Thermal conductivity of crude | 0.14 W/(m•K) | Transmission efficiency of electricity | 99.56% |
| Specific heat capacity of rock | 860 J/(kg•K) | Electricity-heat conversion & transmission efficiency | 95% |
A finite elementary numerical model (FEM) of Well-pair A was established, its simulated domain was dissected by triangle unstructured grids. Meanwhile, grids near the wellbore were refined and optimized to improve the simulation accuracy. Comparison of the calculated results is plotted in Fig. 2.
Fig. 2.
Comparison between the model solutions and simulation results based on Well-Pair A.
From Fig. 2 it can be seen with regard to the median temperature of the well pair, the maximum relative error is 1.40% and the average relative error 0.80%; with regard to cumulative surface energy consumption, the maximum relative error is 0.85% and the average is 0.28%. Clearly, the model solu-tions and simulation results are in good agreement, proving the new model is accurate and reliable.
4. Sensitivity analysis of electric heating parameters
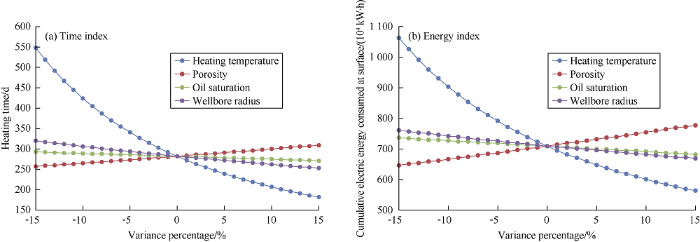
The fluid property data of Well-Pair A indicates that viscosity of the crude there drops below 100 mPa•s at the temperature of over 130 °C, so this temperature is high enough to fulfill the requirement on crude mobility in production stage. Hence, two critical indexes can be used to evaluate the start-up quality of dual-horizontal-well SAGD: (1) The time index: the heating duration required to increase the median temperature of the well pair to 130 °C; (2) The energy index: the cumulative electric energy consumed at surface to increase the median temperature of the well pair to 130 °C.
There are four main factors impacting the start-up quality in the study: (1) heating temperature, (2) wellbore radius, (3) porosity, and (4) oil saturation. Hereby the benchmark scenario was set based on Well-Pair A heated at 240 °C. The changing range of the factors were set at ±15%, and under the condition that one factor changes and the rest factors remain the same, the sensitivity of the time index and energy index were checked respectively, and the results are shown in Fig. 3.
Fig. 3.
Sensitivity curves of electric heating parameters in SAGD start-up.
From the Fig. 3 it can be seen that the sequence of factors with descending sensitivity to the indexes is: heating temperature, porosity, wellbore radius, and oil saturation. Start-up quality is most sensitive to heating temperature, featuring a nonlinear negative correlation. With the heating temperature increasing, the decreasing rates of both time index and energy index slow down. The start-up effect is in positive linear-correlation with porosity, and negative linear-correlation with wellbore radius and oil saturation. In general, variation ranges of the two indexes are greater than that of heating temperature, which indicates the two indexes are more sensitive to heating temperature. In contrast, variation ranges of the two indexes are less than those of porosity, wellbore radius and oil saturation, which indicates the two indexes are less sensitive to these three factors.
5. Case study
Still based on Well-Pair A, temperature distribution near the wellbore, real-time thermal power, temperature rising curves of the oil layer in the middle of the two horizontal wells, surface energy consumption and saved surface energy consumption were calculated with the model. Meanwhile, these indexes between constant-temperature mode and equivalent constant- power mode were compared to find out the variation regularity.
The constant-temperature mode and constant-power mode were compared on the basis that the ultimate energy consumptions of the two modes were equal. Indexes of constant- temperature mode were calculated with the proposed model, while those of constant-power mode were calculated by the model in reference [5].
5.1. The temperature near the wellbore
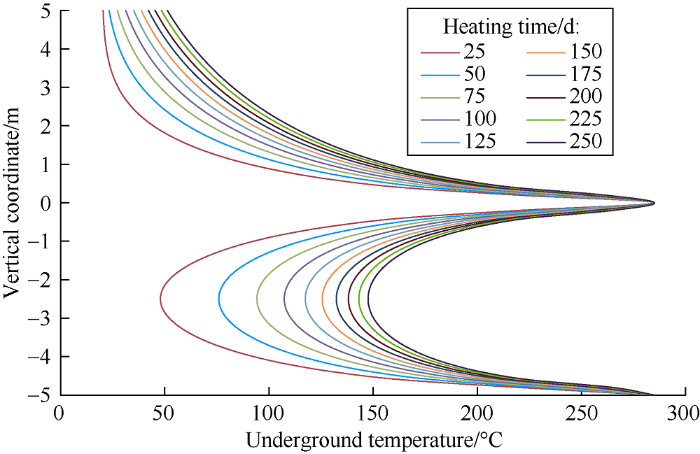
On the profile linking the two wells, the central axis of the upper horizontal section was taken as the horizontal axis (namely axis-L), the midpoint of the upper horizontal section was taken as origin (namely point-O), and the vertical axis passing through the origin was taken as vertical axis (namely axis- H), as illustrated in Fig. 4. Subsequently the underground temperature distribution ±5 m from the horizontal axis at different times during the constant-temperature start-up heated at 285 °C of Well-Pair A were calculated by the proposed model (Fig. 5).
Fig. 4.
The coordinate system on the vertical profile linking two horizontal wells.
Fig. 5.
Underground temperature distribution at different heating times during the constant-temperature start-up at 285 °C of Well-Pair A.
From Fig. 5, it can be seen between the well pair at the same moment the lowest temperature occurs in the middle of the two horizontal sections; the farther the location is from the middle, the higher the temperature will be. Beyond the well pair, the farther the location is from the wellbore, the lower the temperature will be. With the heating going on, different locations differ in the temperature-rising pace: at the location near the wellbore, the temperature rises fast initially and slowly later on, while at the location far from the wellbore, the temperature rising rate is relatively low in the initial stage and decreases slowly later on.
5.2. Real-time reservoir-heating power curves and temperature-rising curves
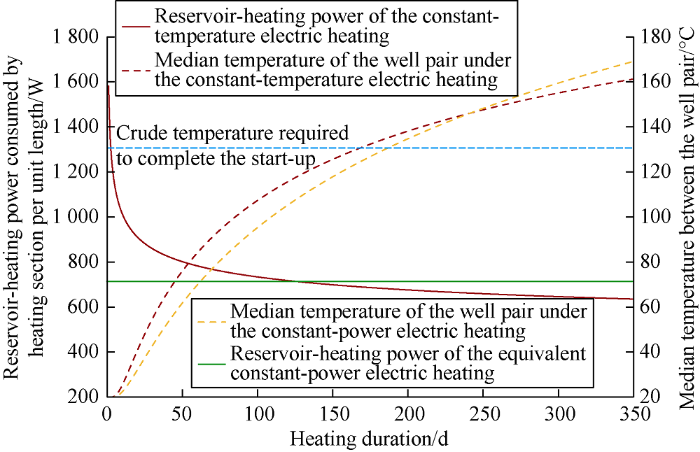
For Well-Pair A heated at constant temperature of 285 °C for 350 d, the real-time reservoir-heating power curves and temperature-rising curves at the middle section were shown in Fig. 6. From the power curves it is found that under the constant-temperature mode the reservoir-heating power consumed is highest at the initial moment and then declines steadily later on, while that under the constant-power mode keeps the same all the time (at 726.30 W/m). From the temperature-rising curves, it can be seen that: (1) Under both modes, a stagnant period occurs at initial stage, suggesting that the heat flux has not spread to the middle section yet, so the temperature in the middle section remains at the initial level. (2) The temperature- rising curves for both modes are in convex shapes, implying the temperature-rising rate is increasingly low. In the earlier stage temperature of middle section under constant-temperature mode rises more rapidly. With the heating going on, temperature-rising curves of both modes intersect at around 238 d, where the temperature of the middle section is around 145 °C, after that temperature-rising rate of constant-power mode surpasses the constant-temperature mode. It takes 166 d to complete the start-up in constant-temperature mode, while 186 d in constant-power mode, manifesting the time needed by constant-temperature mode is 20 days less than that by constant- power mode. It must be noted that the reduction of heating time by constant-temperature mode is based on that temperature of intersection point is higher than that of the terminal start-up temperature. In field practice this condition should also be fulfilled to make the time consumption of the constant-temperature mode shorter than that of the constant-power mode.
Fig. 6.
Real-time power curves and temperature rising curves under different electric-heating modes.
5.3. Relationship between cumulative surface energy consumption and underground temperature rise
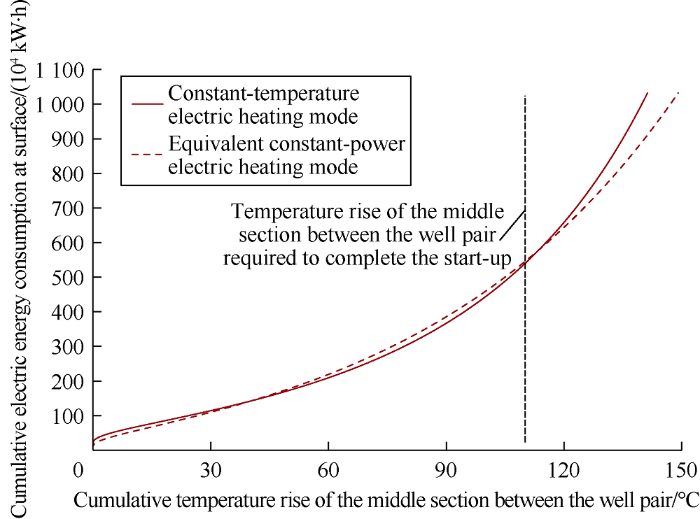
For Well-Pair A heated at 285 °C for 350 d, the relationships between cumulative surface energy consumption and underground temperature rise in the constant-temperature mode and constant-power mode are shown in Fig. 7. It can be seen from the figure: (1) Under both modes, with the rise of formation temperature, the energy consumed to elevate unit temperature increases to some extent, therefore the curves appear in concave shapes. (2) The start-up reaches the expected heating goal when cumulative formation temperature rise in the middle of Well-Pair A reaches 110 °C, at this point the surface electric energy consumption of the constant-temperature mode is 539×104 kW•h, while that of the constant-power mode is 546×104 kW•h, clearly, the constant-temperature mode can save energy consumption by 7×104 kW•h than the constant- power mode. Similarly, this is established on the basis that terminal temperature rise is between those of two points of intersection. In field practice this condition should also be fulfilled to make the energy consumption of the constant- temperature mode lower than that of constant-power mode.
Fig. 7.
Relationships between cumulative surface energy consumption and formation temperature rise under different heating modes.
5.4. Relationships between cumulative energy, water, fuel saved and formation temperature rise
According to the practical experience of Well-Pair A and data from references [12-15], parameters needed to calculate various conservation indexes of the electric heating than steam heating were obtained (Table 2). For Well-Pair A, the relationships between cumulative energy, water, fuel saved and formation temperature rise under constant-temperature mode and constant-power mode than steam heating at heating temperature of 285 °C for 350 d were computed and compared (Figs. 8 and 9).
Table 2 Parameters for calculation of conservation indexes of electric heating than steam heating.
| Name of the parameter | Value of the parameter | Name of the parameter | Value of the parameter |
|---|---|---|---|
| Transmission efficiency of steam | 76.13% | Transmission efficiency of electricity | 99.56% |
| Latent heat of vaporization for steam | 1.639 5×106 J/kg | Electricity-heat conversion & transmission efficiency | 95% |
| Heat value of fuel oil | 41.86×106 J/kg | Heat value of fuel gas under standard condition | 39.82×106 J/m3 |
| Thermal efficiency of the oil-burning furnace | 87.89% | Thermal efficiency of the gas-burning furnace | 86.78% |
| Steam quality coefficient at the furnace outlet | 0.8 |
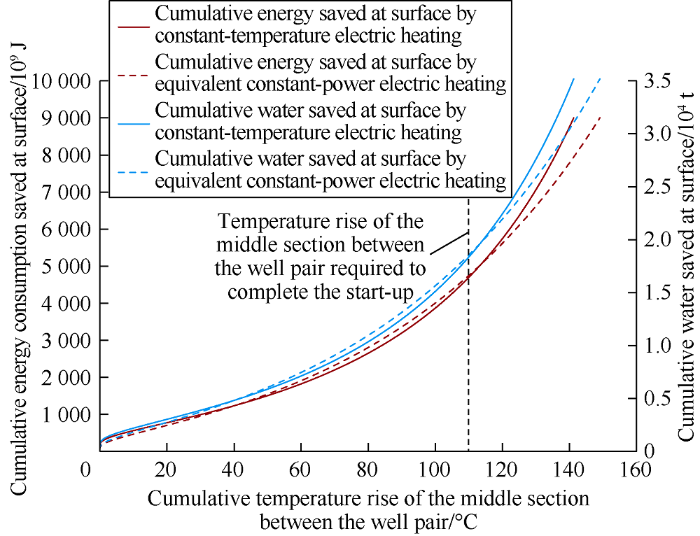
Fig. 8.
Relationships between cumulative energy, water saved and underground temperature rise under different heating modes.
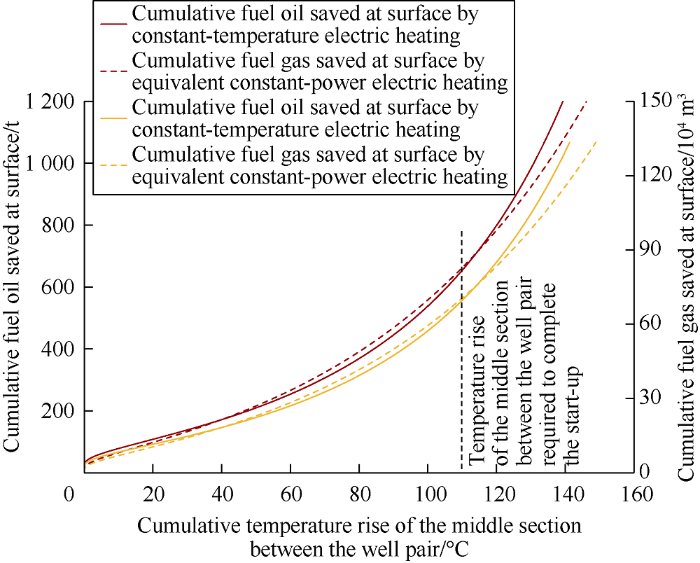
Fig. 9.
Relationships between cumulative fuel saved and formation temperature rise.
Adopting the basic data from Table 2, under the circumstance of same formation energy consumption, surface energy consumption for Well-Pair A by electric heating calculated with Equation (35) is 19.5% lower than that by steam heating. It can be seen from Fig. 8 that constant-temperature heating at 285 °C can save surface energy consumption of 4.70×1012 J and cumulative surface water consumption of 1.84×104 t than steam heating, while the constant-power heating can save surface energy consumption of 4.76×1012 J and surface water consumption of 1.86×104 t in total than steam heating. It can be seen from Fig. 9 that constant-temperature heating at 285°C can save fuel oil of 654 t or fuel gas of 69.7×104 m3 (volume in standard condition) cumulatively than steam heating, while the constant-power mode can save fuel oil of 666 t or fuel gas of 70.9×104 m3 (volume in standard condition) cumulatively than steam heating.
6. Conclusions
A mathematical model for electric heating of dual-horizontal-well SAGD start-up in constant-temperature mode, and methods to calculate energy, water and fuel saved by electric heating than steam heating are established, which have been verified to be accurate and reliable.
Start-up quality is most sensitive to and in nonlinear negative correlation with heating temperature. But it is in positive linear correlation with porosity, and negative linear correlation with wellbore radius and oil saturation.
The proposed model can be used to calculate critical indexes of constant-temperature electric start-up, like underground temperature distribution, energy-consumption parameters and cumulative energy, water and fuel saved by electric heating than steam heating. Moreover, combined with the terminal temperature, the model can predict the time and energy required to complete the start-up.
Nomenclature
a—thermal diffusivity, m2/s;
Hg—heat value of fuel gas under standard condition, J/m3;
Ho—heat value of fuel oil, J/kg;
Hv—latent heat of vaporization for steam, J/kg;
i—serial number of the well or the heater in multiwell (or multiple-heater) operation;
${{K}_{0}}\left( {{x}_{1}} \right)$—modified zeroth-order Bessel function of the second kind;
${{K}_{1}}\left( {{x}_{1}} \right)$—modified first-order Bessel function of the second kind;
l—the length of heating section in a single well, m;
$L\left( {{x}_{1}} \right)$—the operator of Laplace transform;
${{L}^{1}}\left( {{x}_{1}} \right)$—the operator of inverse Laplace transform;
m—number of working wells or heaters;
mo—the mass of cumulative fuel oil consumed by oil-burning furnace during steam heating, which is the conserved amount of fuel oil by electric heating on equal conditions, kg;
mw—the mass of cumulative water consumed to generate steam during steam heating, which is the amount of saved water by electric heating on equal conditions, kg;
${{P}_{\text{ }\!\!\Delta\!\!\text{ }Q}}$—the percentage of surface energy consumption saved by electric heating than steam heating, %;
qf—thermal power consumed by the heater inside the wellbore, W;
qf, m—the sum of thermal power consumed by heaters inside wellbores during multiwell operation, W;
qh—heat flux in real domain, J/(m2•s);
${{\tilde{q}}_{\text{h}}}$—heat flux in Laplace domain, J/m2;
qs—thermal power consumed at surface, W;
qs, m—the sum of electric power consumed at surface during multiwell operation, W;
qw—heat flux on the wellbore, J/(m2•s);
Qf—cumulative thermal energy consumed by formation, J;
Qf, m—cumulative thermal energy consumed by formation during multiwell operation, J;
Qg—cumulative energy consumption at surface in steam heating, J;
Qs—cumulative electric energy consumed at surface, J;
Qs, m—cumulative electric energy consumed at surface during multiwell operation, J;
ΔQ—cumulative energy consumption saved at surface by electric heating than steam heating, J;
r—distance from the axis of the wellbore, m;
rD—dimensionless distance from the axis of the wellbore;
rw—wellbore radius, m;
s—Laplace variable, dimensionless;
t—heating time, s;
tD—dimensionless heating time;
T—underground temperature at a given point, °C;
T0—initial underground temperature, °C;
TD—dimensionless temperature increment of the reservoir;
Th—heating temperature, °C;
${{\tilde{T}}_{\text{D}}}$—dimensionless temperature increment in Laplace domain;
ΔT—temperature increment of the reservoir at a given point in real domain, °C;
ΔTm—temperature increment of the reservoir at a given point in real domain during multiwell operation, °C;
Vg—the volume of cumulative fuel gas consumed by gas-burning furnace under standard condition during steam heating, which is the amount of fuel gas saved by electric heating on equal conditions, m3;
x—steam quality coefficient at the furnace outlet, dimensionless;
x1—independent variable of a function;
${{\delta }_{\text{ct}}}$—the loss rate during electricity-heat conversion & transmission, %;
${{\delta }_{\text{e}}}$—the loss rate during the transmission of electricity, %;
${{\delta }_{\text{v}}}$—the loss rate during the transmission of steam, %;
${{\eta }_{\text{bg}}}$—the thermal efficiency of the gas-burning furnace, %;
${{\eta }_{\text{bo}}}$—the thermal efficiency of the oil-burning furnace, %;
${{\eta }_{\text{ct}}}$—electricity-heat conversion& transmission efficiency, %;
${{\eta }_{\text{e}}}$—the transmission efficiency of electricity, %;
${{\eta }_{\text{v}}}$—the transmission efficiency of steam, %;
λ—the comprehensive thermal conductivity of the reservoir, W/(m•K);
${{\tau }_{\text{D}}}$—the dimensionless moment when the heating terminates under a certain heating temperature.
Reference
A new optimization method for steam-liquid level intelligent control model in oil sands steam-assisted gravity drainage (SAGD) process
Production improvement of heavy-oil recovery by using electromagnetic heating
Applicability and assessment of micro-wave assisted gravity drainage (MWAGD) applications in Mehsana heavy oil field, India
Quantifying heat requirements for SAGD startup phase: Steam injection, electrical heating
DOI:10.2118/165578-PA URL [Cited within: 1]
Analytical solution for double-horizontal-well SAGD electirc preheating model of heavy oil resevoirs.
Finite element modeling of reservoir heating by an electrical cable
Field control technology of combustion assisted gravity drainage (CAGD)
Mechanisms and influencing factors of the oil bank in fire flooding
Parameters tuning of PID controller and its application
Algorithm 368: Numerical inversion of Laplace transforms
DOI:10.1145/361953.361969 URL [Cited within: 1]
Remark on algorithm 368: Numerical inversion of Laplace transforms
Real-time energy losses calculating and analyzing in the transmission network
Injected steamheat loss and production rate of SAGD
Analysis of influencing factors and heat efficiency of oil-fired boiler
Analysis of heat efficiency of gas-fired boiler