Introduction
Horizontal well fracturing with multiple stages and clusters is used to develop tight sandstone reservoirs efficiently by generating densely transverse hydraulic fractures (HFs) perpendicular to the wellbore and enlarging a reservoir drainage area[1,2,3,4]. However, production logging data indicates that 30% or more of perforation clusters are insignificant to oil and gas production[4]. Both reservoir heterogeneity and well cementation quality can result in an uneven contribution of production between perforation clusters. Moreover, reservoir heterogeneity includes lithology and stress state heterogeneities and natural fracture density. Well completion quality involves stage spacing, number of perforation clusters and cluster spacing, pumping rate, fracturing fluid type, proppant amount per stage, and fracture initiation sequence. Previous studies have shown that strong stress interference between the multiple HFs with short stage spacing, called stress shadow effect, significantly affects propagation path and HF width[2, 5-14]. Pre-existing HFs can deflect the subsequent ones, even forming a longitudinal HF along the horizontal wellbore. In addition, the HFs in the middle of the clusters are subjected to higher compressive stress in the same fracturing section, thereby resulting in a decrease in the HF width or conductivity. This condition may even cause the HFs to stop extending or merge, thus leading to nonuniform reservoir stimulation and reduction in production after fracturing. The fracture initiation and propagation of multi- staged horizontal well fracturing have been extensively studied theoretically. However, the direct physical experiment for verification has yet to be conducted. Furthermore, existing studies have excluded the influence of net pressure in the previously created HFs and cementing quality of the horizontal section on the distribution of multiple fractures in horizontal wells.
In view of the above issues, based on true tri-axial hydraulic fracturing modeling system, an experimental method modeling the initiation and propagation of fractures in multi-staged horizontal well fracturing was designed in this work. The experiment considered the additional stress caused by different net pressures, analyzed the influence of horizontal stress difference, perforation depth, fluid pressure in existent fracture and cementation quality of horizontal section on the propagation form of hydraulic fractures. After summing up the features of fracturing curve, some cases were examined according to the experimental results.
1. Theoretical model of the induced stress field
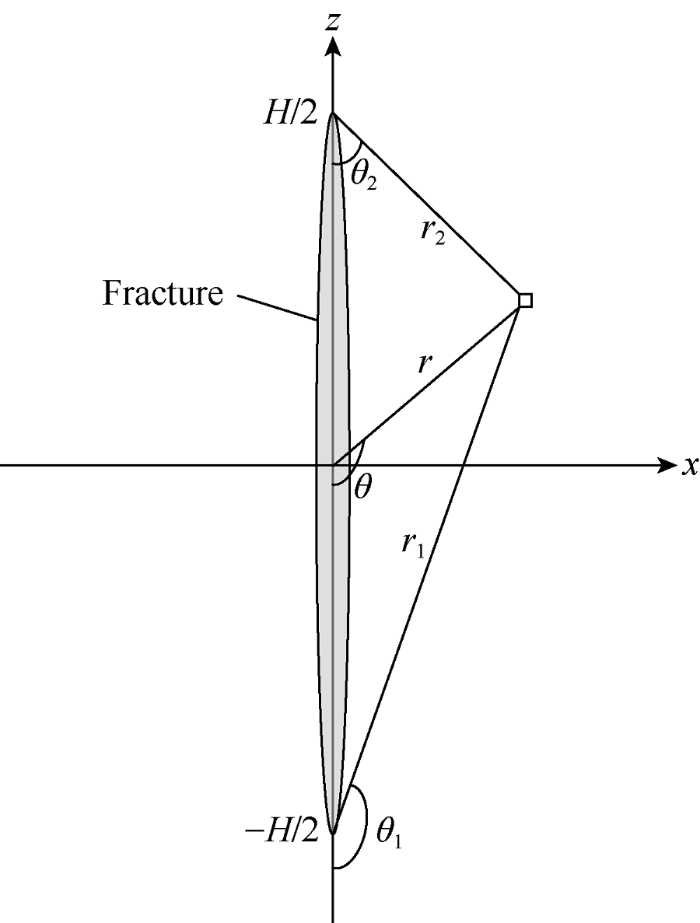
Multi-staged hydraulic fracturing produces many HFs in the reservoir, from which stress interference arises. Fundamentally, stress interference is an induced stress field generated by the opening HFs. The superposition of induced stresses on the in-situ stress field will change the in-situ stress. Notably, the stress interference is related to HF geometry. When the HF length is longer than the height, a cross-section perpendicular to the HF length is approximate to the plane strain. The HF height that affects the stress field is the characteristic quantity that controls the deformation of the rock matrix[2]. Generally, the HF length is much longer than the height. Thus, the induced stress field is calculated on the basis of height. For the 2D fixed-height HF (Fig. 1), according to the Sneddon formula[15,16], the HF induced stress field is:
Fig. 1.
Fig. 1.
Induced stress field model of a fixed-height vertical HF.
where $r=\sqrt{{{x}^{2}}+{{z}^{2}}}$, $r_{1}=\sqrt{(x+0.25H)^2+z^{2}}$,
$r_{1}=\sqrt{(x-0.25H)^2+z^{2}}$, $\theta =\arctan \left( \frac{z}{x} \right)$,
${{\theta }_{1}}=\arctan \left( \frac{z}{x+0.5H} \right)$, and ${{\theta }_{2}}=\arctan \left( \frac{z}{x-0.5H} \right)$
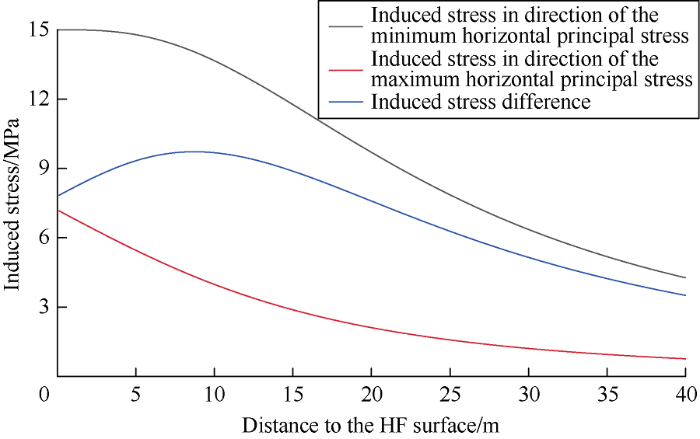
The induced stress distribution perpendicular to the fracture surface is calculated using Formula (1) with a net pressure of 15 MPa and an HF height of 40 m (Fig. 2). In addition, the induced stress in the direction of the minimum horizontal principal stress decreases slowly and then rapidly with the increase of the distance between the pre-created HF surface and the stress. Furthermore, the induced stress in the direction of the maximum horizontal principal stress tends to decrease gently with the increase in distance. A maximum value was observed in the induced stress bias ${{\sigma }_{\text{c}xx}}-{{\sigma }_{\text{c}yy}}$ ($\Delta \sigma $)versus the distance curve in which the induced stress bias increases initially and then decreases with the increase in distance.
Fig. 2.
Fig. 2.
Induced stress versus the distance to the HF surface.
When the induced stress field is added to the in-situ stress field, the horizontal stress bias near the cracked HF may be reversed. That is, the ratio of the induced stress bias to the original horizontal principal stress bias is larger than 1, thereby causing the HF to be deflected toward the original minimum horizontal principal stress. Moreover, a 90° turn even occurred to form a longitudinal HF. Therefore, the change in the original horizontal principal stress bias can be measured by the induced stress bias[17,18,19,20,21,22].
2. Physical simulation of a multi-staged horizontal well
2.1. Apparatus and procedure
The He-8 section in the block of SU53 of Sulige gas field was selected as the target zone, with 0.87×10-3 μm2 average permeability, 9.0% average porosity, 24.7 GPa uniaxial elastic modulus, 0.24 Poisson’s ratio, 2.2 MPa tensile strength, and 61.3 MPa and 49.2 MPa maximum and minimum horizontal principal stresses, respectively.
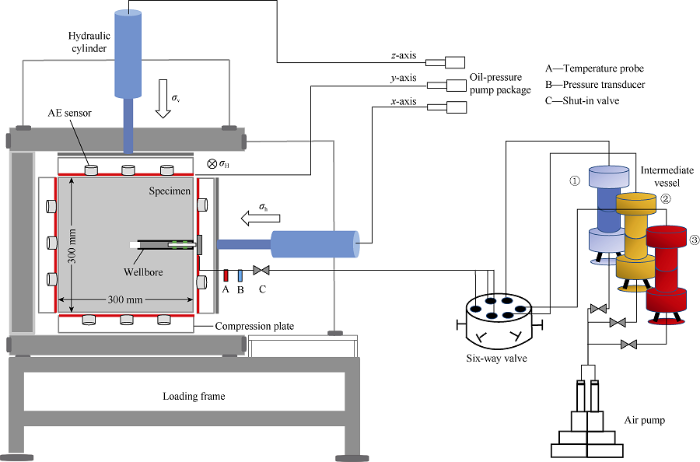
A true triaxialhydraulic fracturing simulation system was adopted in this experiment[14] (Fig. 3), in which the real in-situ stress field was achieved by the crustal differential coefficient. The compression plates were slowly pushed through an oil- pressure pump package. A hydraulic cylinder was used to impose pressures triaxially on a specimen in the chamber. The highest loading stress of the x- axis is 15 MPa, but those of the y- and z- axes could reach 30 MPa. The fracturing fluid was extruded into the experiment pipeline after loading stress of the chamber, which flowed through a six-way valve and entered the modeling wellbore to fracture the rock sample by pushing the piston in the intermediate vessel with an air pump. Simultaneously, real-time variation data of temperature and pressure were recorded by transducers connected to the pipelines.
Fig. 3.
Fig. 3.
Schematic of the true triaxial hydraulic fracturing simulation system (modified according to Reference [14]).
Concrete cubic samples with a dimension of 30 cm × 30 cm × 30 cm were fabricated in the study (Fig. 4). The specimen with similar physical properties to natural rocks is a hybrid combined with cement, sand and water for a proportion of 3:1:1, respectively. Well cementation was realized by inserting an experimental wellbore into the specimen before finishing the sample.
Fig. 4.
Fig. 4.
Concrete specimen and modeling multi-staged horizontal wellbore.
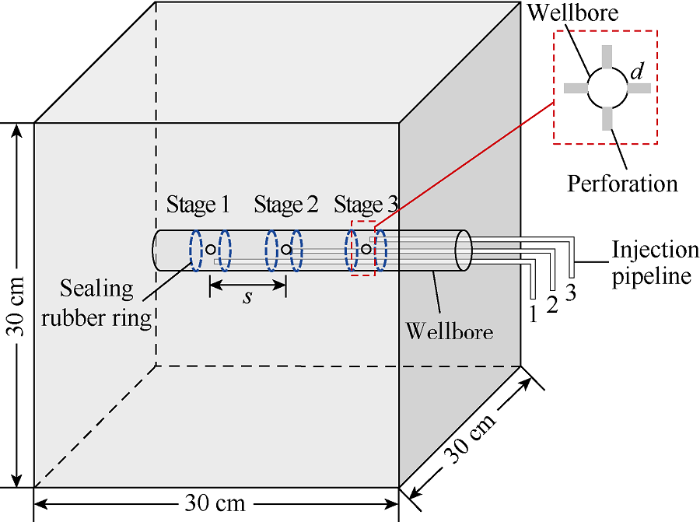
A modeling wellbore that can be reused was designed and produced to simulate the multi-staged hydraulic fracturing process in a horizontal well (considering three stages in this simulation) (Figs. 4 and 5). The model consisted of an exterior casing, an interior wellbore and three injection pipelines; these materials could be assembled by inserting the exterior casing into the interior wellbore.
The outer casing was a steel tube with 2.0 cm and 1.6 cm external internal diameters, correspondingly, and 20.0 cm length (Fig. 5a). Four through-holes with a 3 mm diameter were drilled in the center of each stage at a 90° phase angle. The perforations (steel tubes with a slotted surface and 3 mm external diameter) were welded vertically to the holes to mimic an actual perforating channel. Spiral grooves with a 1 mm depth and a 2 mm width were cut at a 3 mm interval on the surface of the external casing to model high-quality cementation, which was handled by sand-blasting to enhance the bond degree between the concrete and outer surface of the steel casing. By contrast, the outer surface of the steel casing was smoothed to simulate poor quality cementation.
Fig. 5.
Fig. 5.
Schematic of the modeling wellbore of multi-staged horizontal hydraulic fracturing.
The inner wellbore was a steel tube with 1.5 cm and 0.8 cm external and internal diameters (Fig. 5b). The outlet holes with a 3 mm diameter on the internal wellbore were drilled at the positions opposite the perforations on the exterior casing. The swelling rubber rings were used as packers to seal the annular situated at the corresponding perforation stage.
The external and internal diameters of the injection pipeline are 3 mm and 2 mm, correspondingly. For a separate injection, the outlet of each steel pipeline was located at the midpoint of the corresponding fracturing stage of the inner wellbore, wherein the sealing steel sheets were also welded in case of fracturing fluid that flows into the two other working stages. Then, the other end of each pipeline was connected to the corresponding intermediate vessel through the six-way valve. Consequently, the fracturing fluid was pumped into an individual stage by opening the valves required on the six-way valve with others closed when injecting fluid in one vessel into the rock sample.
The specific experimental procedures are as follows:
Step 1: Connect the pipelines and place the specimen into the chamber of the experimental system. The wellbore should be in the x-axis direction.
Step 2: Push the hydraulic piston into the chamber. Then, apply vertical stress along the z-axis up to the setting value and maintain stability, with maximum and minimum horizontal principal stresses in the y- and x- axis directions, respectively.
Step 3: Connect the three pipelines inside the wellbore with the six-way valve and link the three intermediate vessels containing fluid mixed with dye for different colors to the six-way valve. Vessel numbers 1, 2, and 3 included blue, green and red dyeing agents, correspondingly.
Step 4: Open the valves connected to the pipeline and the intermediate vessel required to inject fluid. Keep the other valves shut. In particular, vessel number 1 and the pipeline inside Stage 1 form a pair when fracturing the first stage and so on. Then, turn on the injection system, pump fracturing fluid into the wellbore at a constant rate and record the wellhead pressure variation using the pressure transducer during the entire experimental process until the designed amount of fluid is reached. Finally, turn off the pumping station and shut the valves when pressure fluctuates slightly.
Step 5: During the experimental process, pressure may keep a low level in the created fracture given the HF that probably extends to the boundaries of the specimen and fracturing fluid coming out of the cracks. Turning on the injection system and pumping fluid with high viscosity into the pre-created fractures are necessary to prevent the undesirable phenomenon. These processes can be performed by connecting the pipeline inside the stage fractured with the vessel that contains highly viscous fluid through the six-way valve, thereby effectively maintaining a certain pressure magnitude in the created fractures and impeding fracture closure. This operation can simulate a process in which proppants and fracturing fluid support the fractures after pumping has stopped.
Step 6: After fracturing Stage 2, adjust the appropriate valves and follow Step 5 for fractured stage 1. Then, repeat Step 4. Subsequently, manipulate the correct valves and implement Step 5 for fractured Stages 1 and 2. Thereafter, repeat Step 4 to fracture Stage 3.
Step 7: Take out the concrete sample and distinguish the HFs of different stages in accordance with the dyeing color on the rock surface. Then, split the specimen with a wire cutting apparatus to analyze the propagation routes of HFs in the vicinity of the wellbore in detail.
2.2. Experimental parameters
Injection and wellbore parameters were specified on the basis of similarity theory. In particular, injection parameters were designed in accordance with the theoretical research conducted by Liu et al. (2000)[23]. Specifically, injection parameters were calculated on the basis of the scaling principle by combining the pumping rate and fracturing fluid viscosity adopted in the field with dimensions of concrete samples and operation parameters in the experimental system[23,24]. Therefore, the experimental pumping rate was set to 50 mL/min with 120-160 mL accumulative pumping volume and 63 mPa·s fluid viscosity over the field condition that the pumping rate is 3.5-5.0 m3/min and the net pressure is 15-25 MPa.
Furthermore, wellbore parameters were established by the geometry scaling law. The geometry scaling relationship between the modeling and real stage spacing is calculated as follows:
The stage spacing and fracture half-length of multi-staged horizontal fracturing treatment in the field are 40-70 m and 250-350 m, correspondingly. Thus, the experimental stage spacing was set to 1.75-5.60 cm under the hypothesis that the modeling fracture half-length was 15-20 cm. The 2 cm small stage spacing and 5 cm large spacing facilitated experimental comparison. Notably, the effect of perforation on the initiation pressure of HFs was expected to be studied in the present study. Therefore, the perforation depth (1-5 cm) was set one to five times the wellbore diameter to diminish the influence of additional stress field near the wellbore on the fracture initiation.
The applied in-situ stress in this study was specified on the basis of the normal fault stress mechanism (${{\sigma }_{\text{v}}}\ge {{\sigma }_{\text{H}}}>{{\sigma }_{\text{h}}}$). Considering the concepts of horizontal stress differential coefficient and dimensionless net pressure defined by Beugelsdijk et al.[22] who conducted experiments on HF propagation in multiple fracture media, the experimental conditions were designed through the values of horizontal stress differential coefficient and dimensionless net pressure, thereby determining the leak-off of fluid into natural fractures and fracture deviation degree.
The reservoir stress differential coefficient is 0.25, and the maximum and minimum horizontal principal stresses of the targeted zone are 61.3 MPa and 49.2 MPa, respectively. The aforementioned factors were used to define the experimental applied stress conditions (Table 1). It should be noted, the pre-existing fractures were either open or close during the subsequent fracturing treatment. Specifically, the fracture produced earlier would be in critical close state when the dimensionless net pressure of fluid inside the fracture is low (i.e. equal to zero) after pumping ceased; while the fracture formed earlier would be open when the dimensionless net pressure is high (i.e. equal to two).
Table 1 Experimental parameters and cementation quality.
| Specimen No. | In-situ stress state | Stage spacing/cm | Perforation depth/cm | Cementation quality | Dimensionless net pressure in HF | |||
|---|---|---|---|---|---|---|---|---|
| σv/MPa | σh/MPa | σH/MPa | Kh | |||||
| 1 | 20 | 8 | 16 | 1.00 | 2 | 1 | good | 0 |
| 2 | 20 | 8 | 10 | 0.25 | 2 | 5 | good | 0 |
| 3 | 20 | 8 | 10 | 0.25 | 5 | 1 | good | 0 |
| 4 | 20 | 8 | 16 | 1.00 | 2 | 1 | good | 2 |
| 5 | 20 | 8 | 10 | 0.25 | 2 | 5 | good | 2 |
| 6 | 20 | 8 | 10 | 0.25 | 2 | 5 | poor | 0 |
Six specimens were fractured in this study (Table 1). No. 1-5 were good in cementation quality; while No. 6 was poor in cementation quality.
3. Characteristics of multiple fracture propagation and pressure curves
3.1. Influence of net pressure in pre-created HF on multiple fracture geometry
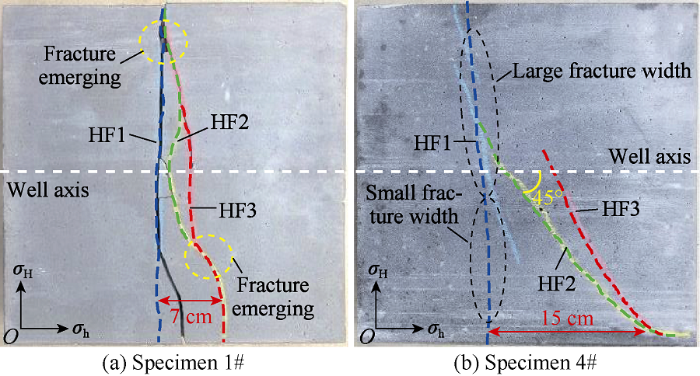
The experiment was conducted with 1.00 horizontal stress difference coefficient, 2.0 cm experimental stage spacing, and 1.0 cm perforation depth. The HF propagation pattern of Specimen 1# with zero net pressure and Specimen 4# with net pressure twice the horizontal stress bias are illustrated in Fig. 6. In this figure, HF1 of both specimens tended to extend along the horizontal maximum principal stress to form a transverse HF. Remarkably, HF1 within Specimen 1# grew evenly on both sides, and the HF width was symmetrically distributed (Fig. 6a). However, HF1 in Specimen 4# mainly initiated at the upper side of the wellbore, where the propagation and width of the HFs were sufficient. By contrast, the width at the lower side of the wellbore was small, thereby leading to an asymmetrical pressure distribution of subsequent injection (Fig. 6b).
Fig. 6.
Fig. 6.
Influence of net pressure in pre-created HFs on multiple fracture geometry.
3.1.1. Critical distance of stress interference
The critical distance of stress interference is used to measure the maximum range of induced stress. When Specimen 1# was subjected to fracturing Stage 2, HF1 was under critical closure situation, and HF2 was deflected away from HF1 by a certain angle. Then, the lower side was biased to the original maximum horizontal principal stress at the distal end of the wellbore. Moreover, the stress interference was weakened, thus indicating that the critical distance of stress interference perpendicular to fracture surface was 7 cm, and the corresponding field critical distance was 93 m (Fig. 6a). The net pressure of HF1 within Specimen 4# was twice the horizontal stress bias, and the lower sides of HF2 and HF3 were deflected away from HF1 to the boundary at an angle of approximately 45°, thereby denoting that the critical distance of HF1 was at least 15 cm and the corresponding actual critical distance was likely to be more than 200 m (Fig. 6b). Consequently, a large net pressure in the cracked HF indicated a long critical distance of stress interference.
3.1.2. Multiple fracture merging
The upper side of HF2 in Specimen 1# was deflected to and merged with HF1 at the distal end. Furthermore, HF3 was also merged with HF2 after deflecting by a small angle (Fig. 6a), thereby indicating that emerging of multiple HFs could occur when the horizontal wells are segmentally fractured at a small stage spacing in the conventional sandstone reservoir with a high horizontal stress bias. The fluid pressure at the distal end of the upper part of HF1 was reduced due to fluid friction and loss, thus possible even terminating the HF and weakening stress interference. Although the subsequent HFs were within the critical distance of the pre-fractured ones, the induced stress field variation had deflected the horizontal maximum principal stress toward HF1. The propagation path of HF2 after deflection coincided with HF3 considering the short stage spacing, which was merged with HF2 only after initiation.
3.1.3. Asymmetric fracture propagation
In contrast to Specimen 1#, the upper propagation of HF2 and HF3 in Specimen 4# were suppressed (Fig. 6b). The asymmetric loading of the fluid pressure in HF1 caused a strong stress interference on the upper side of HF1 and a large additional principally induced stress in the direction of the minimum principal stress perpendicular to the surface of the fracture. Furthermore, the extension stopped with short propagation distance after initiation. If the proppant is unevenly laid in the HFs of tight reservoirs, then the HF length where the proppant was laid was longer when the HF is closed. The compression state of the formation near the HF was maintained, and the phenomenon of stress interference of the subsequent HFs was evident. By contrast, the effective support is unformed in the HF given low sand concentration, and the compression state of the formation near the HF was released with small induced stress. Therefore, the degree of nonuniformity of the proppant placement within the HF will also affect the propagation of subsequent HFs.
3.1.4. Characteristics of pressure curves
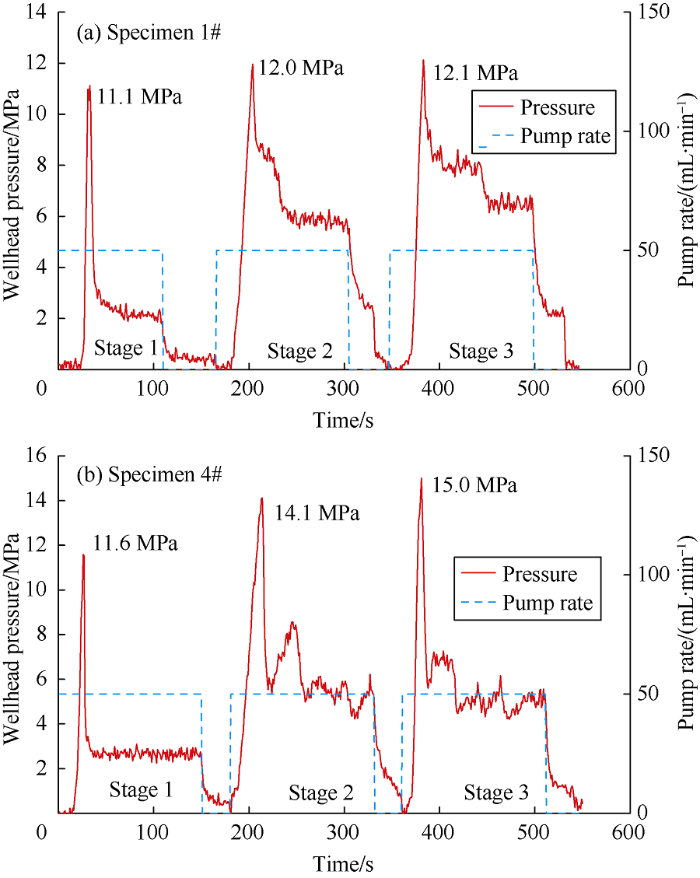
The fracture initiation pressure of subsequent HFs increased given the superposition of induced stress fields. When the dimensionless net pressure was zero, the fracture initiation pressures of HF2 and HF3 in Specimen 1# increased by 8.1% and 9.0% with respect to HF1, correspondingly (Fig. 7a). Moreover, when the dimensionless net pressure was two, the fracture initiation pressures of HF2 and HF3 in Specimen 4# increased by 21.6% and 29.3%, respectively (Fig. 7b). Therefore, the increase of the fracture initiation pressure was positively correlated with the net pressure within the pre-existing HFs.
Fig. 7.
Fig. 7.
Pumping pressure curve under various net pressures in the pre-created HFs.
In Fig. 7, the extension pressure of HF1 in the two specimens was relatively flat, whereas that of the extension pressure of the subsequent HFs fluctuated evidently. Moreover, a large dimensionless net pressure indicates a severe fluctuation. This condition was due to the flat and transverse HF1. Thus, the flow resistance of the fracturing fluid was small and the extension pressure was stable. However, the flow resistance was large and the pressure fluctuated drastically with tortuous and narrow HFs given the deflection of subsequently HFs. Therefore, the treatment parameters can be optimized by judging the HF geometry and stress interference on the basis of the pumping pressure curve.
3.2. Influence of stage spacing and perforation parameters on multiple fracture geometry
The experiment was conducted with a 0.25 horizontal stress difference coefficient and zero dimensionless net pressure of 0 in the pre-created HFs. The result indicated that stage spacing plays a crucial role in the propagation of multiple HFs. When the experimental stage spacing was 2 cm which is equal to 30 m in the field, having deflected away from the wellbore, the subsequent HFs in Specimen 2# were gradually deflecting away from the previous ones (Fig. 8a). Furthermore, when the stage spacing increased to 5 cm which is equal to 80 m in the field, HF1 and HF2 within Specimen 3# propagated approximately perpendicular to the horizontal wellbore, whereas HF3 deflected away from HF2 (Fig. 8b). In Fig. 2, the horizontal minimum principal stress on both sides of the cracked HFs can be increased under critical closure situation, thus resulting in the deflection of subsequent HFs. However, the subsequent fracturing sections tend to be in the induced stress decreasing zone given the large stage spacing. Consequently, HF2 in Specimen 3# is hardly disturbed by stress inference, whereas HF3 is deflected under the superposition of stress interference.
Fig. 8.
Fig. 8.
Influence of stage spacing on multiple fracture geometry.
The perforation parameters significantly affect fracture initiation pressure. The experiment was performed with perforation depths of 5 cm and 1 cm in Specimen 2# and 3#, correspondingly. The pumping pressure curve showed that the fracture initiation pressures of each stage were 18.8%, 18.9% and 9.5% lower in Specimen 2# than in Specimen 3# (Fig. 9). This condition is due to the augmentation of the effective area of the liquid pressure on borehole with the increase in the depth and length of the perforation and amplification of the liquid energy for rupturing the formation, thereby causing the circumferential stress of the perforation tunnel to rise and the formation fracture pressure to decrease[25]. In addition, in the case in which the small stage spacing is equivalent to a high perforation density, the distance between the perforation tunnels decreases with the increase in the perforation density and porous stress concentration effect, thus resulting in an increase in stress near the tunnels. Therefore, the reduction in breakdown pressure can be attributed to the mutual influence of stress concentration caused by a few tunnels in infinite objects[26]. The fracture initiation pressure can be reduced by perforation with intense density and deep penetration in the field.
Fig. 9.
Fig. 9.
Pressure curve under various stage spacing and perforation parameters
3.3. Influence of horizontal stress bias on multiple fracture geometry
The horizontal stress difference coefficient, stage spacing, perforation depth and dimensionless net pressure in pre-existing HFs were set to 0.25, 2.0 cm, 5 cm and 2 respectively. The multiple fracture propagation pattern of Specimen 5# was similar to that of Specimen 4#. Additionally, HF1 was also transverse and perpendicular to the wellbore. Furthermore, HF2 and HF3 were deflected at a certain angle (Fig. 10a). However, the propagation process was apparently different. Initially, longitudinal HF2 in Specimen 5# extended to the perforation tunnel of HF3, thereby causing HF3 to overlap with HF2 after initiation. Then, both of the HFs propagated away from HF1 at a deflection angle of approximately 60° (Fig. 10b).
Fig. 10.
Fig. 10.
Influence of horizontal stress bias on fracture geometry.
Horizontal stress variation is defined as:
where $\frac{r}{H}$ is the dimensionless distance. $\sigma _{\text{c}xx}^{{}}$ and $\sigma _{\text{c}yy}^{{}}$ in equation (1) are substituted to equation (5) and obtain
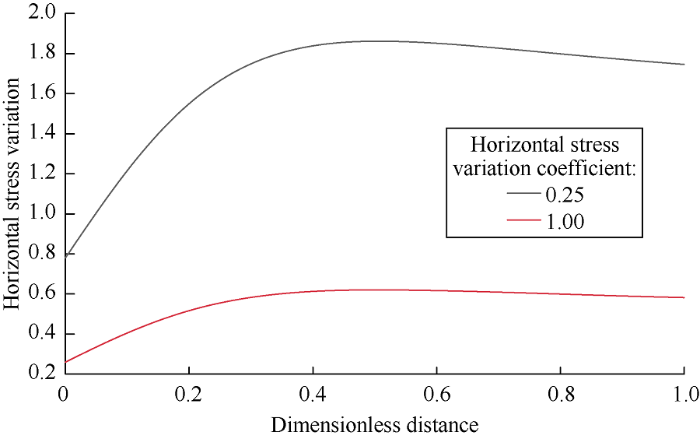
In equation (6), the horizontal stress variation was related not only to the HF height, distance between HF and HF surface, and Poisson's ratio of the rock but also to the horizontal stress bias. Stress reversal will occur if horizontal stress variation was larger than one. The experiment was conducted using the HF height of 30 cm and Poisson's ratio of 0.24. The relationship between the dimensionless distance and horizontal stress variation under different horizontal stress biases was plotted on the basis of the in-situ stress parameters of Specimen 4# and 5# (Fig. 11).
In Fig. 11, the stress reversal could occur with constant net pressure in the fracture under low horizontal stress bias, and the region of stress inversion is broad. The horizontal stress variation was more than one when the distance from HF1 to subsequent HFs is more than 1.5 cm because the horizontal stress difference coefficient of Specimen 5# is 0.25. In this case, the pre-created HFs significantly affect the subsequent ones, and a longitudinal HF might even be formed because of stress reversal. Therefore, the deflection angle of HF2, which extends a distance along the horizontal wellbore, and the angle of HF3 is larger in Specimen 5# than bigger than in Specimen 4#.
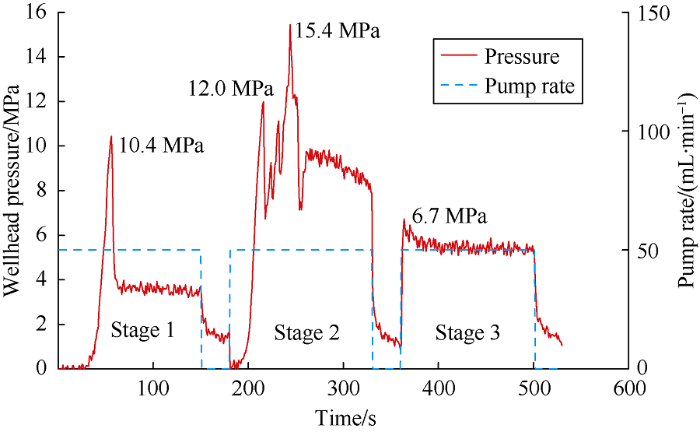
The pressure curve patterns of Specimen 5# were slightly different from fracturing section to section (Fig. 12). Longitudinal HF2 was initiated at the junction of the wellbore and rock, which was reflected on the pressure curve as two peak values of 12.0 and 15.4 MPa, followed by a rapid decrease in the extension pressure of 7.14-9.15 MPa. No significant breakdown pressure was observed because HF3 communicated with HF2. The subsequent injection pressure was higher than HF1 because HF2 was tortuous. The fracture initiation pressure of each section of Specimen 5# no longer showed a tendency to rise in turn because HF2 became a longitudinal HF.
3.4. Influence of cementing quality of horizontal section on multiple fracture geometry
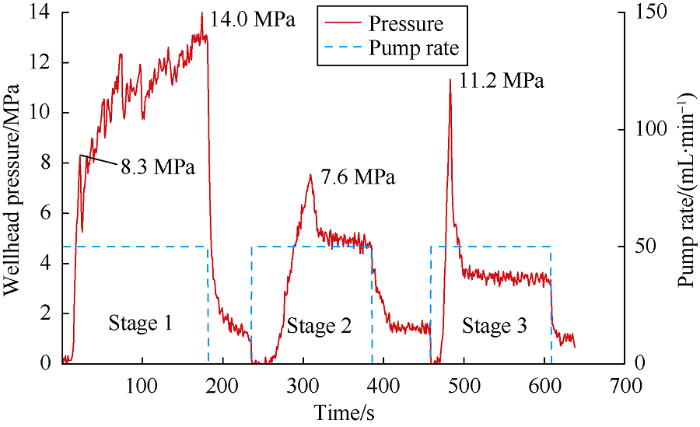
The smooth outer wall of the wellbore was in contact with a specimen, which represents a poor cementing quality. The results of Specimen 6# show (Figs. 13 and 14) that HF1 was initiated at the joint between the wellbore and the specimen (perforation heel), thereby forming a longitudinal HF approximately parallel to the wellbore, and the pressure was slightly reduced after reaching 8.3 MPa, and then slowly and significantly fluctuated to a high peak of 14.0 MPa (Figs. 13 and 14). The longitudinal HF pressure curve of HF1 contained multiple peak values similar to the pressure variation in HF2 in Specimen 5#. Moreover, the fracture initiation and extension stages were hard to distinguish and both under high pressure. The overall pressure of HF2 was low, similar to HF3 in Specimen 5#, and HF2 communicated with HF1 once HF initiated. The formation of a new HF again was difficult. Therefore, in the horizontal well section with poor cementing quality, the stress near the wellbore changed given the cracking of the joint between the wellbore and specimen. Moreover, HF has a favorable chance of forming a longitudinal HF, thereby affecting the propagation path of the subsequent ones, and reducing the stimulated reservoir volume.
Fig. 13.
Fig. 13.
Influence of poor cementation quality on fracture morphology.
Fig. 14.
Fig. 14.
Pressure curve with poor cementation quality.
4. Case study
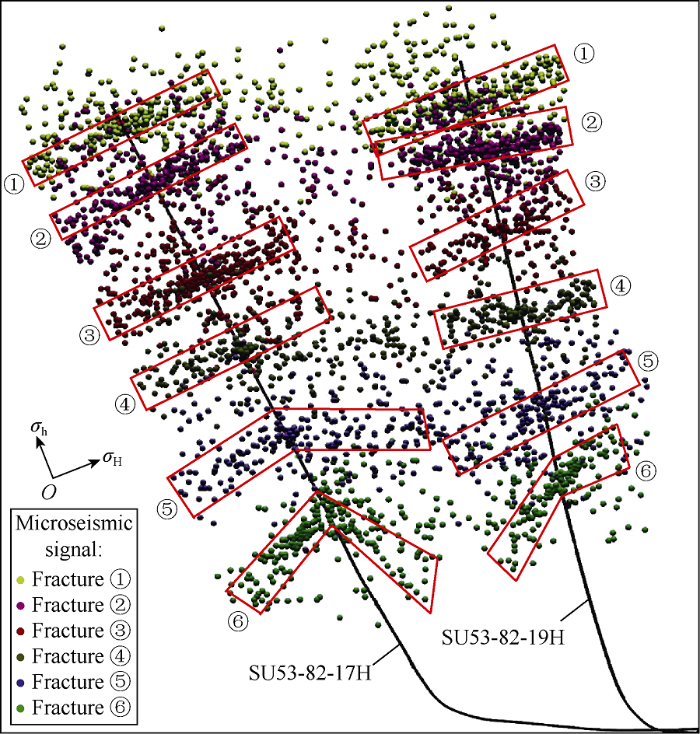
SU53-82-17H and SU53-82-19H are two six-stage-fractured horizontal wells in the Su53 block. For SU53-82-17H, the designed stage spacing lies in the range of 130-150 m and the average dimensionless net pressure is 1.1. However, the stage spacing and average dimensionless net pressure are 110-125 m and 1.8, correspondingly. The microseismic monitoring was performed to depict and obtain the real-time fracture propagation during hydraulic fracturing (Fig. 15).
Fig. 15.
Fig. 15.
Results of microseismic fracture monitoring (Numbers ①-⑥ are HFs).
Three following essential features were revealed in fracture propagation: (1) Subsequent fracture propagation among Numbers ①-④ had not been interfered violently, with propagation paths still extending in the direction of the maximum horizontal principal stress. The probable reason is that follow- up fractures were situated in the induced stress-decreasing zone given large stage spacing, and low fluid net pressure might cause a short critical distance of stress interference. (2) Multiple fractures were emerging on the underside of fractures ① and ② of SU53-82-19H considering relatively high horizontal stress bias (10 MPa) and small stage spacing. (3) The fractures located in the intermediate section were generally under comparatively low stress interference. By contrast, a fracture that is close to the heel indicated an evident deviation degree with the superposition of induced stress.
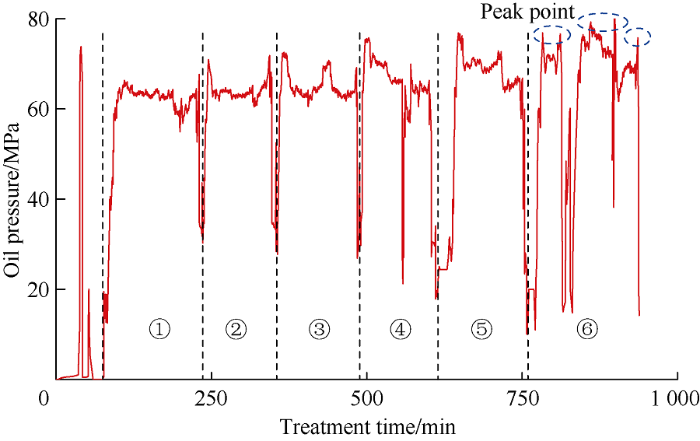
An interesting phenomenon is the occurrence of deflection with a large angle on the upside of fracture ⑥ of SU53-82- 17H. This situation is a result of horizontal stress variation degree that is greater than one given a horizontal stress bias that is less than the net pressure in created fractures, with an increased probability to form a longitudinal fracture instead. In Fig. 16, pressure fluctuated at a high level with multiple peak points, thereby indicating that HFs initiated at the junction of wellbore and formation and producing a tortuous and narrow fracture along the wellbore. That is, the corresponding stage has worse quality of cementation. Furthermore, fracture ⑥ of SU53-82-19H propagated asymmetrically due to the nonuniform proppant placement in fracture ⑤ according to the results of Specimen 4#. The propagation on the upside of fracture ⑥ was restrained because the upper propped fracture with large width maintained a compression state.
Fig. 16.
Fig. 16.
Pressure curve of multi-staged fracturing in SU53-82- 17H (Numbers ①-⑥ are HFs).
In summary, the fracture propagation laws and characteristics of pressure curves gained in the experiment can be applied to explain and analyze the factual fracture geometry in the field, to provide several useful guidelines for optimizing fracturing treatment parameters.
5. Conclusion
In this study, the stress interference critical distance is approximately 93 m with the pre-existing fracture critically closed (dimensionless net pressure equal to zero). Moreover, the multiple fracture propagation tends to emerge under high horizontal stress difference and small stage spacing. However, the stress interference critical distance will be greater than 200 m for the dimensionless net pressure of the created fracture equal to two. Furthermore, the asymmetric distribution of the pre-existing fracture width can cause an uneven induced stress field and restrain a subsequent fracture propagation under high net pressure. In addition, follow-up fractures are supposed to distribute in induced stress-decreasing zone on the condition of large stage spacing, thus weakening stress interference and obscuring fracture deflection. From the perspective of field treatment, dense perforation with deep penetration has enhanced the fluid energy subject to the pore wall and porous stress concentration, in which initiation pressure has been reduced effectively. For the effect of horizontal stress bias, horizontal stress variation will be increased under low bias when fluid net pressure is constant in the created fracture. Furthermore, the deviation angle and probability of forming a longitudinal fracture rise when horizontal stress variation is greater than one. A new finding exists that if cementation quality is poor, HFs tend to initiate at the junction between the wellbore and the reservoir, and produce a longitudinal fracture along the wellbore axis.
In terms of the pressure curve characteristics, the initiation pressure of each working stage displays a successive increase trend in multi-staged horizontal fracturing. Particularly, the growth extent of pressure is presumed to be 30% when the dimensionless net pressure in created fractures reaches two. Furthermore, three pressure features exists with respect to a formed fracture geometry in which a steep drop and a low extension of pressure were observed after initiation for transverse fractures. Pressure reduces by a slight degree and fluctuates decreasingly at a high level during the extension stage to produce a tortuous narrow fracture after initiation. Conversely, pressure fluctuates increasingly and significantly when longitudinal fractures formed, thereby indicating multiple peak points and ambiguous bound between the initiation and extension stages.
Nomenclature
d—perforation depth, cm;
f—horizontal stress variation degree, dimensionless;
H—fracture height, m;
Kh—horizontal stress differential coefficient, dimensionless;
L—fracture half-length, m;
pf—fluid pressure in the pre-existing fractures, MPa;
pnet—fluid net pressure in the pre-existing fractures, MPa;
pnetD—dimensionless net pressure;
s—stage spacing, cm;
x, y, z—Cartesian coordinates, m;
σh—minimum horizontal principal stress, MPa;
σH—maximum horizontal principal stress, MPa;
σv—vertical stress, MPa;
Δσ—induced stress bias , MPa;
σcxx, σcyy, σczz—induced normal stress when fractured, MPa;
v—Poisson’s ratio, dimensionless.
Subscripts:
M—physical experimental data;
F—field data.
Reference
Volume fracturing technology of unconventional reservoirs: Connotation, optimization design and implementation
DOI:10.1016/S1876-3804(12)60054-8
URL
[Cited within: 1]

The connotation, design optimization and implementation of the Volume Fracturing technique are discussed. The connotation includes five aspects as follows: (1) break up reservoirs to form complex fracture network, and “artificial” permeability; (2) the fracture initiation involving not only single open-fracture but shear failure and slip; (3) “breakthrough” the traditional fracturing seepage theory model, greatly shorten the effective fluid seepage distance; (4) more suitable for highly brittle formations; and (5) multi-stage and multi-cluster perforation mode to improve well productivity. Research shows that: the time required to seep through matrix with 0.000001 × 10613 μm2 permeability to fracture for 100 m distance is about more than 100 × 104 years, and only Volume Fracturing can realize the “shortest distance”seepage. Cluster spacing optimization, non-uniform stage (cluster) interval and proppant filling mode are the key to achieve Volume Fracturing. Small cluster interval technology, multiple stop-injection construction mode and tip screen-out fracturing technology are the key techniques to realize Volume Fracturing in low brittle formations. Volume fracturing technique has a good application prospect in tight oil (gas), volcanic and carbonate reservoirs, and the further developed “integrated” volume fracturing (based on multi-layer and multi-branch well technology) is the future development direction for unconventional resources.
Stress interference calculation model and its application in volume stimulation of horizontal wells
DOI:10.1016/S1876-3804(16)30101-X
URL
[Cited within: 3]

A new model for calculating stress fields of fractured media was established by incorporating stress correction factor based on displacement discontinuity boundary element method. The accuracy of the new model is close to 3D displacement discontinuity model, and its calculation is significantly simplified. An algorithm for multi-fracture propagation geometry was proposed based on fracture criterion and fracture growth rate law, which was used to investigate multi-fracture stress interference and propagation geometry. The results show that the size of stress interference is determined by the shortest dimension of fracture face, which is 1.2 1.5 times fracture height when fracture length is longer than fracture height, and 1.2 1.5 times fracture length when fracture length is shorter than fracture height. The larger the ratio of fracture spacing to fracture height, or the smaller the ratio of net pressure to the differential principle stress, the more close to well-bores the deviation position is, and the larger the deviation angle is. The middle fracture propagates to the fracture at a further distance and one dominating fracture propagates longest when three-cluster fractures are not equally spaced, while the middle fracture propagates straightly when three-cluster fractures are equally spaced.
The relationship between fracture complexity, reservoir properties, and fracture treatment design
Evaluation of production log data from horizontal wells drilled in organic shales
Altered-stress fracturing
DOI:10.2118/17533-PA URL [Cited within: 1]
Fracturing aspects of horizontal wells
DOI:10.2118/18542-PA URL
Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures
Simultaneous hydraulic fracturing of adjacent horizontal wells in the Woodford Shale
Experimental investigation of the interaction among closely spaced hydraulic fractures
A numerical simulation of the inter-cluster interference in multi- cluster staged fracking for horizontal wells
DOI:10.3787/j.issn.1000-0976.2014.01.011
URL

Multi-cluster staged fracking is a key technology to develop low permeability and unconventional reservoirs,with which,the stimulated reservoir volume(SRV)can be increased significantly,so as to enhance the oil or gas production and ultimate recovery.In order to study the interference between fractures of different clusters in multi-staged fractured horizontal wells,a three-dimension finite element model for simulating the propagation of fractures was established.The model was theoretically based on fluid-solid coupling equations in porous medium and damage mechanics,and zero-thickness cohesive element was adopted to simulate the rock damage during the initiation and propagation of artificial fractures.Factors affecting the inter-cluster fracture interference in multicluster staged fracking,including perforation cluster numbers,cluster spacing,reservoir and treatment parameters,were researched by a series of simulations.The results showed that the perforation cluster numbers and spacing are two primary factors.Based on the model,the cluster spacing of a horizontal well was optimized.As a result,the production of this well was distinctively improved compared with that of the adjacent well,which proves that the model is feasible and reliable in optimizing the design of multi-cluster staged fracking for horizontal wells.
Distribution rules of earth stress during zipper fracturing of shale gas horizontal cluster wells
The analysis of crack interaction in multi-stage horizontal fracturing
DOI:10.11764/j.issn.1672-1926.2015.03.0533
URL

Multi-stage horizontal fracturing has been widely used in the field with the inevitable crack interaction.Crack interaction is conducive to initiation and extension of fractures,which forms complex fracture network and improves reservoir conductivity.However,crack interaction also has adverse effects on hydraulic fracturing resulting in poor stimulation.Based on the theory of elasticity,mathematical models are established to study the effects of crack interaction in multiple cluster fractures,from the aspects of initiation pressure,fracture width and the position of fracture.The study shows that it is hard to get successful stimulation with serious crack interaction because the phenomenon such as change of fracture width resulting from crack interaction.To get the relationship of cluster space,fracture height and crack interaction,a sensitivity analysis is conducted.The result indicates that the cluster space should be reasonable to avoid the adverse effects of crack interaction.The study result contributes to the optimization of the stimulation of multiple stages horizontal well.
Numerical investigation of hydraulic fracture network propagation in naturally fractured shale formations
DOI:10.1016/j.jsg.2016.01.004
URL
[Cited within: 2]

613D DEM-based complex fracturing model for shale formations is presented.61Shale plastic deformation decreases the complexity of hydraulic fracture networks.61Distribution of natural fractures may determine whether HFN can grow uniformly.61Optimized perforation clusters placement enhances uniformly distributed HFN.
The distribution of stress in the neighborhood of a crack in an elastic solid
DOI:10.1098/rspa.1946.0077
URL
[Cited within: 1]

The distribution of stress produced in the interior of an elastic solid by the opening of an internal crack under the action of pressure applied to its surface is considered. The analysis is given for 'Griffith' cracks (2) and for circular cracks (3), it being assumed in the latter case that the applied pressure varies over the surface of the crack. For both types of crack the case in which the pressure is constant over the entire crack surface is considered in some detail, the stress components being tabulated and the distribution of stress shown graphically. The effect of a crack (of either type) on the stress produced in an elastic body by a uniform tensile stress is considered and the conditions for rupture deduced.
The opening of a griffith crack under internal pressure
DOI:10.1090/qam/17161 URL [Cited within: 1]
Optimization design and application of horizontal well staged fracturing in tight gas reservoirs
DOI:10.7623/syxb201305018
URL
[Cited within: 1]

A field study on the optimization design and application of horizontal well staged fracturing for Shaximiao tight sandstone gas reservoir in western Sichuan was carried out.It used induced stress field model of horizontal well staged fracturing which was establish to improve the overall percolation ability of reservoir.Meanwhile,fracture initiation sequence,fracture spacing and perforation parameters were optimized.And the optimization of fracture net pressure and displacement communicated natural fractures around the main fractures.The field implementation of horizontal well staged fracturing demonstrated that:fracture segments increased to 8-13 after optimization,with2-3 clusters in each perforating section and a length of 0.5 m for per cluster,and the cluster spacing of the same fracture segment was 30-60 m;these variable density perforation parameters were 12-16 holes/m in the middle,16-20 holes/m at two terminals,and displacement reached to 3.5-6.5 m3/min;the average steady production of5 wells by using optimization method was 5.3 104 m3/d,increasing significantly compared with previous status,and it also obtained significant economic benefits.The optimized design method can provide a reference for optimization design of similar tight gas reservoirs.
Fracture propagation laws in staged hydraulic fracturing and their effects on fracture conductivities
DOI:10.1016/S1876-3804(17)30035-6
URL
[Cited within: 1]

Completely taking into account the interferences between fractures as well as the friction effects on injection allocations, a fully coupled finite element method inherited from a verified one is proposed to discuss fracture propagation laws and analyze their impacts on fracture conductivities. Simulations show that although fractures have similar injection allocations that fluctuate around the allocation averaged by fractures, interferences between them lead to their different propagation rates and some fractures even stop propagating for a while. Shorter fractures generally have higher pressure and smaller pressure gradients than longer ones. The pressure differences between fractures result in long fractures having bottlenecking zones far away from the wellbore, and make them vulnerable to screen-out at the inlets and the bottlenecking zones. The effects of the propagation laws on fracture conductivities include: (1) the conductivities in short fractures are weakened by rapid proppant settlement in them; (2) long fractures may lost their conductivities due to screen-out near the wellbore; (3) the conductivities in long fractures decrease because of screen-out at the bottlenecking zones.
Numerical simulation of multi-stage fracturing and optimization of perforation in a horizontal well
DOI:10.1016/S1876-3804(17)30015-0
URL
[Cited within: 1]

Aiming at analyzing the issues of non-uniform growths of multiple hydraulic fractures caused by stress shadowing, a numerical model considering elasto-hydrodynamic, stress interference and flow distribution into different fractures was presented. Based on the model, the effects of perforation friction, perforation cluster spacing, Young modulus of rock and fracturing fluid viscosity on the growth of multiple fractures were investigated. The simulation results show that the growths of hydraulic fractures are relatively uniform with adequate perforation friction; the reduction of perforation cluster spacing, increase of Young modulus or fluid viscosity will cause the reduction of some fracture width and uneven flow distribution into these fractures, thus aggravating non-uniform growth of multiple fractures. Since appropriate perforation friction is conducive to the uniform growth of fractures, a convenient quantitative optimization method to calculate the needed perforation friction for uniform growth was proposed. By estimating inter-fracture induced stress during fracturing, the perforation friction coefficient needed to maintain uniform growth of fractures inside a stage is calculated, and reasonable engineering parameters of perforation can be selected based on this. The perforation parameters of a horizontal well were calculated with the proposed method, the simulation results and actual fracturing performance show that the optimized perforation parameters can effectively keep uniform growth of fractures.
Algorithm for multi-fracture propagation morphology in horizontal well volume fracturing: Investigation on different fracture distribution patterns
Experimental study on the mechanism of hydraulic fracture growth in a glutenite reservoir
DOI:10.1016/j.jsg.2017.02.012
URL
[Cited within: 1]

61Fracturing tests were performed on large natural glutenite specimens.61Effect of gravel size, stress, and fluid parameters on fracture growth was studied.61Intersections modes include termination, penetration, diversion and attraction.61Fracture pattern in glutenite with large gravels tends to be tortuous.61Breakdown pressure may increase significantly in high-strength gravels.
Experimental hydraulic fracture propagation in a multi-fractured medium.
Similarity criterion in simulation experiment of hydraulic fracturing
Hydraulic fracture propagation geometry and acoustic emission interpretation: A case study of Silurian Longmaxi Formation shale in Sichuan Basin, SW China
Study of effect of hydraulic perforating on formation fracturing pressure
Effect of perforation on initiation and propagation of hydraulic fracturing in tight sandstone gas reservoirs