Introduction
Drilling ultra-deep wells is faced with complex geological conditions, high temperature, high pressure, and large well depth etc., so formation fluid invasion into the wellbore is inevitable. Higher formation pressure often results in higher casing pressure after overflow well shut-in, so the drill string in the well would bear large uplift force under the action of high fluid pressure. When the gravity of the drill string and the friction of the shut-in seal are insufficient to suppress the uplift force caused by overflow, the drilling tool may be broken or washed out of the wellbore, resulting in blowout out of control. In the drilling process of an ultra-deep well in Xinjiang, when drilling to 693 m deep, an overflow of 0.5 m3 was found. When the well was shut down according to the “five-seven” code, the well had a standpipe pressure of zero, casing pressure soaring to 21.5 MPa, and the drill string was pushed up 2.7 m. When a well in Daqing Oilfield was drilled to 211 m, the drill tools uplifting happened, resulting in bending of drill pipe and damages to water hose and traveling car[1]. There is some understanding on the drill tools uplift caused by annulus pressure build-up[2,3], but there is still a lack of theoretical analysis on the mechanism of the drill string uplift, the mechanism of high pressure fluid acting on the drill string to produce the uplift force, and the relationship between the uplift force and buoyancy. Therefore, this work has attempted to find out the mechanics mechanism of drill string uplift from the basic forces exerting on drill string in hydraulic environment. Meanwhile, the non-circulating multiphase flow theory was used to analyze the change of wellbore pressure, and the evolution and density distribution of gas-liquid two-phase flow during shut-in to obtain the variation of axial load on drill string during overflow well shut-in and the formation conditions of the uplift of drill string, which would provide theoretical support for wellbore safety during ultra-deep well drilling.
1. Mechanism of drill string uplift after overflow shut-in
1.1. Mechanical model of drill string
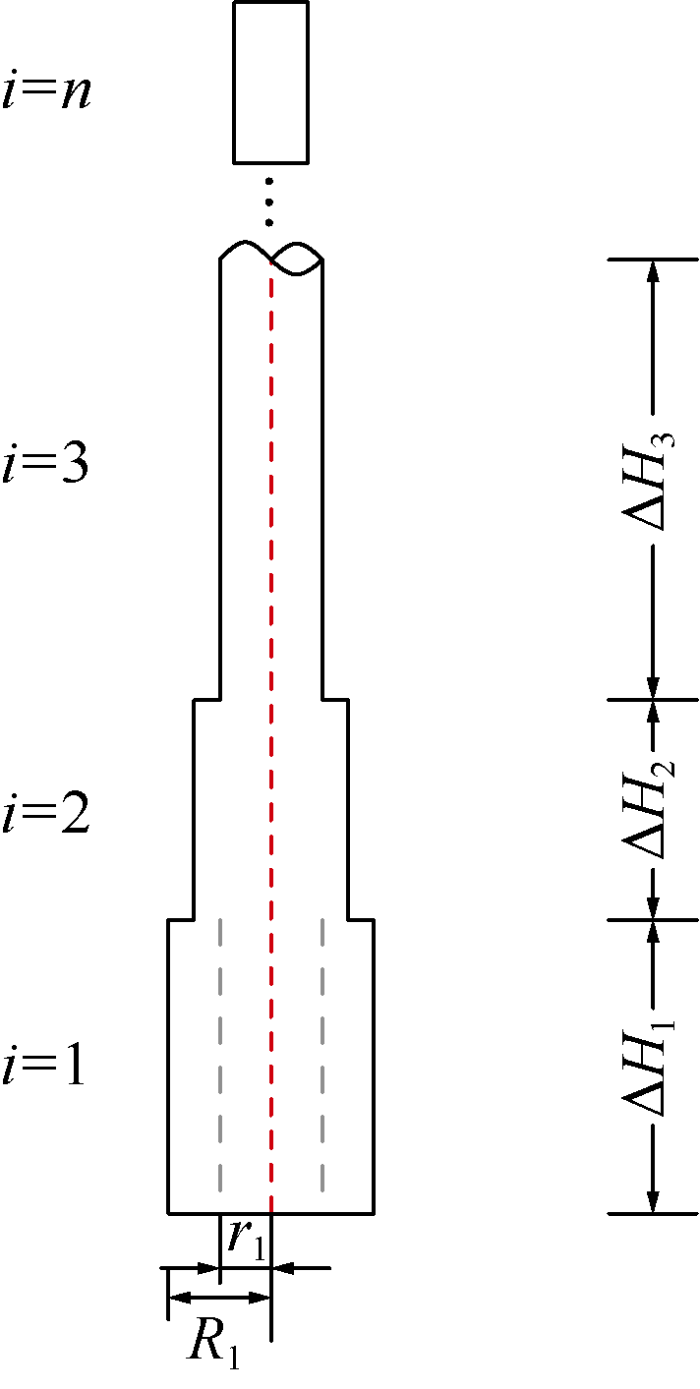
Suppose there is one set of bottomhole assembly (BHA) composed of drill pipes of different sizes of n sections, as shown in Fig. 1. The density of drilling fluid inside and outside the drill string are different. The cross-section method for analyzing internal force in material mechanics and the pressure area method in hydrostatics were used to establish the model to solve the axial force at any cross-section a below the wellhead.
Fig. 1.
Fig. 1.
Combined drill string composed of drill pipes of different sizes.
The BHA below section a is considered as a whole (including drill string and drilling fluid in the drill string), and the force model is shown in Fig. 2. The mass of each drill string section is composed of its own mass and the fluid mass in it. Therefore, the mass of the first and second drill string sections are as follows:
Fig. 2.
Fig. 2.
Force model of drill string in hydrostatic pressure.
Fig. 3.
Fig. 3.
Relationship between axial load of wellhead and casing pressure.
For each drill string section below section a, the resultant force of liquid pressure acting on the sidewall of the drill tool is zero, so only the pressure acting on the section and shoulder side of the drill string are considered, and the resultant force is positive in the opposite direction of gravity. The pressure of the fluid is:
According to the static equilibrium relationship, the pulling force at the cross section a can be expressed as:
The equations (1)-(5) are substituted into (6):
where ${{K}_{i}}=\text{1}-\frac{R_{i}^{2}{{\rho }_{\text{o}}}-r_{i}^{\text{2}}{{\rho }_{\text{i}}}}{\left( R_{i}^{2}-r_{i}^{\text{2}} \right){{\rho }_{\text{s}}}}$
In equation (7), the ΔHiqiKi is the gravitational force of each drill string section in drilling fluid, that is, the buoyant weight. Since qi is the average weight per unit length, the gravity of joints has been taken into account, and the influence of shoulders and joints need not be considered in the calculation of buoyant weight[4,5].
1.2. Mechanism of drill string uplift
The first item on the right side of equation (7) is the buoyant weight of the drill string, and the second item is deformed to obtain:
Fx in equation (8) is the virtual force generated by hydraulic pressure. The concept and calculation method of virtual force are derived from the mechanical analysis of column instability under hydraulic environment[6,7,8]. The virtual force is the axial force really exists, not virtual. The American Petroleum Society named it effective bucking force. The two kinds of axial force can be connected by virtual force, that is, the real axial force is equal to the difference between the effective axial force and the virtual force[9]. In equation (7), Ta is the true axial force of cross-section a.
In equation (9), Te is the effective axial force, which is the accumulation of the buoyant weight of the drill string from each section, and the direction is consistent with the direction of gravity. Therefore, the uplift force on the drill string can only be generated by the virtual force. When the virtual force is opposite to the gravity direction, it is the uplift force on the drill string. Therefore, the uplift force on the drill string is derived from hydraulic pressure rather than buoyancy.
1.3. The maximum casing pressure condition to prevent the uplift of the drill string
In ultra deep well drilling, the blowout preventer is installed in the drill string, when the standpipe pressure is zero, the equation (8) is simplified into:
At this time, Fx is the uplift force, but the existence of uplift force on the drill string does not necessarily mean the appearance of drill string uplift. Only when the uplift force on the drill string is larger than the drill string buoyant weight, the uplift of the drill string will appear. Therefore, the condition
for preventing the uplift of the drill string is:
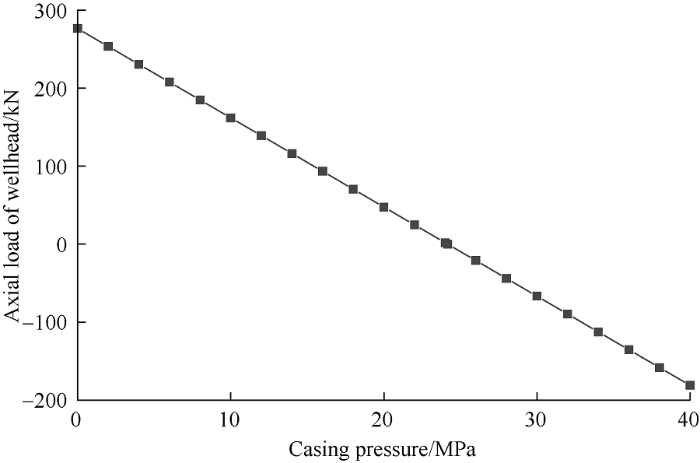
Assuming that overflow occurred in a well and the well was shut in. When the well was shut in, the drilling collar (with outer diameter of 120.7 mm) remained in the well is 500 m, the drilling fluid density is 1.5 g/cm3, and the drilling collar weight per unit length is 683 N/m. The relationship between wellhead axial load and wellhead casing pressure as shown in Fig. 3 can be calculated by equations (1)-(10).
When the casing pressure is greater than 24.16 MPa, the axial load of the wellhead is negative, and the uplift force is greater than the buoyant weight of the drill string, so the drill string uplift will occur. In order to prevent the drill string uplift, the casing pressure at the wellhead should be controlled at less than or equal to 24.16 MPa, that is to say, the maximum casing pressure at the top of the drill string is 24.16 MPa. As for when the maximum casing pressure would be reached, it is necessary to conduct dynamic analysis of fluid migration and wellbore pressure evolution during shut-in.
2. Calculation model for uplift force of drill string during overflow shut in
During the overflow well shut-in stage, the change of casing pressure and wellbore overflow state will lead to constant change of wellhead axial load. On the one hand, the increase of casing pressure leads to the increase of uplift force, on the other hand, the change of density of mixture in the wellbore causes the change of the buoyant weight of drill string. In order to accurately calculate the change of axial load of the drill string during overflow shut-in, it is necessary to analyze the change process of wellbore pressure and gas-liquid mixture state during shut-in. The change of wellbore pressure and wellbore overflow state after shut-in is the result of both wellbore after-flow and gas slippage effects[10,11,12]. In the early stage of shut-in, the bottom hole pressure is less than formation pressure. Under the action of pressure difference, the formation gas continues to invade into the wellbore, the wellbore fluid is compressed, the bottom hole pressure and wellhead pressure increase. When the bottom hole pressure equals to the formation pressure, the formation gas stops invading into the wellbore, which is the wellbore after-flow effect. Since the gas density is lower than the density of drilling fluid, the gas will slip off and the gas volume will expand and compress the wellbore fluid during the ascending process, resulting in an increase of the bottomhole and wellhead pressure, which is the gas slippage rise effect.
2.1. Calculation model of wellbore after-flow effect after overflow shut-in
Under the effect of wellbore after-flow, the formation fluid continuously invades into the wellbore under the pressure difference. The influx amount is related to the thickness and permeability of the reservoir, and the gas properties. The infiltration velocity can be calculated by the theory of seepage mechanics:
Since the volume of the wellbore annulus is constant, the formation fluid influx volume per unit time is equal to the volume of fluid reduced in the wellbore per unit pressure, which is:
The bottom hole pressure at time t during after-flow can be calculated:
where $Y=\frac{{{p}_{\text{e}}}+{{p}_{\text{w0}}}}{{{p}_{\text{e}}}-{{p}_{\text{w0}}}}\exp \left[ \frac{1.076{{p}_{\text{e}}}{{K}_{\text{r}}}{{h}_{\text{r}}}{{B}_{\text{g}}}t}{\left( {{V}_{\text{g}}}{{C}_{\text{g}}}+{{V}_{\text{l}}}{{C}_{\text{l}}} \right)T{{Z}_{\text{g}}}\mu \ln \frac{{{r}_{\text{e}}}}{{{r}_{\text{w}}}}} \right]$
2.2. Calculation model of gas slippage effect after
overflow shut-in
Since the density of formation gas is lower than the density of drilling fluid, the gas slips and rises, and the density and pressure at each position of the wellbore change with time and space, which should be calculated with the time and space grid method. Moreover, the position and length of the gas- liquid two-phase segment change during the rise of gas. Therefore, in this study, two grid systems were adopted. For the wellbore annulus, the static mesh analysis method was used to divide the wellbore annulus into X grids, and the grid size and number were constant. For the gas-liquid two-phase segment, the dynamic mesh analysis method was used to divide the two-phase segment into Z meshes. The number of meshes didn’t change with time, but the mesh size hg(t,z) changes continuously with the rise of gas. The volume increment of gas due to expansion equals to the sum of the volume of the drilling fluid reduced by compression and the volume of the drilling fluid lost to the formation, which is:
The calculation of gas holdup in the gas-liquid two-phase unit is:
The formula for calculating the unit pressure of gas-liquid two-phase is:
The calculation formula of gas-liquid two-phase unit length is:
The formula of gas slippage velocity is as follows:
When the wellbore pressure is greater than the formation pressure, the drilling fluid will be filtered into formation through the mud cake[13], and the drilling fluid loss is:
2.3. Comprehensive calculation model of uplift force on drilling string
The wellbore volume is constant throughout the shut-in process. Within a unit time, the volume of fluid flowing into the wellbore minus the volume of fluid flowing out plus the volume of slipping and swelling equals to the volume of fluid in the wellbore reduced by the increase of wellbore pressure, which is:
The simultaneous equations (12)-(21) were solved by Gauss-Seidel iteration method to get the relationship between fluid density and wellbore pressure in the wellbore with time, and then the relationship was substituted into equation (9) to obtain the dynamic change of the uplift force of the drill string during shut-in.
3. Case study
Overflow well shut-in happened in a well in Xinjiang during the trip and the overflow rate was 3 m3 when the well was shut-in. The well structure and BHA are shown in Tables 1 and 2. The formation parameters were: the thickness of drilled gas reservoir of 2.5 m, the permeability of the gas reservoir of 10×10-3 μm², the formation pressure of 120 MPa, and the geothermal gradient of 0.02 °C/m. The parameters of drilling fluid and mud cake were: the density of drilling fluid of 1.8 g/cm³, the viscosity of drilling fluid of 40 mPa·s, the solid content of drilling fluid of 5%, the solid content of mud cake of 15%, the volume coefficient of drilling fluid of 0.000 4 MPa-1, and the permeability of mud cake of 0.000 2×10-3 μm².
Table 1 Structure of the well of the fourth drilling section.
| Profile name | Outer dia- meter/mm | Inner dia- meter/mm | Beginning depth/m | End depth/m |
|---|---|---|---|---|
| Casing | 196.85 | 171.45 | 0 | 5 250 |
| Casing | 206.38 | 174.38 | 5 250 | 5 909 |
| Open hole | 165.10 | 5 909 | 6 170 |
Table 2 Parameters of bottomhole assembly distribution.
| Drilling tool name | Outer diameter/mm | Inner diameter/mm | Length/ m | Weight per unit length/(N·m-1) |
|---|---|---|---|---|
| Bit | 165.1 | 38.10 | 0.23 | 620.25 |
| Drill collar | 120.7 | 57.20 | 180.00 | 683.00 |
| Drill pipe | 101.6 | 84.83 | 5 989.77 | 233.34 |
3.1. The variation of wellbore pressure with shut-in time
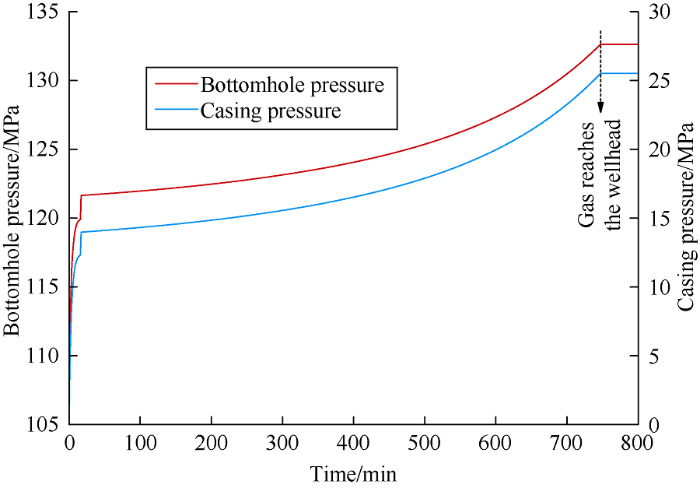
As shown in Fig. 4, the bottom hole pressure and casing pressure increase with time. In the first 20 min, the wellbore after-flow effect was dominant, followed by the gas slippage effect. After 747 min, the gas slipped to the wellhead and the casing pressure was 25.5 MPa. When the gas reached the wellhead, because the gas didn’t rise anymore, the gas volume would not change, casing pressure would remain unchanged, and at this time the casing pressure was the maximum casing pressure during shut-in. The calculated pressure changes in this study are the same as those obtained by Lage et al.[14]
Fig. 4.
Fig. 4.
Variation of wellbore pressure with shut-in time.
3.2. The critical drill string length of uplift
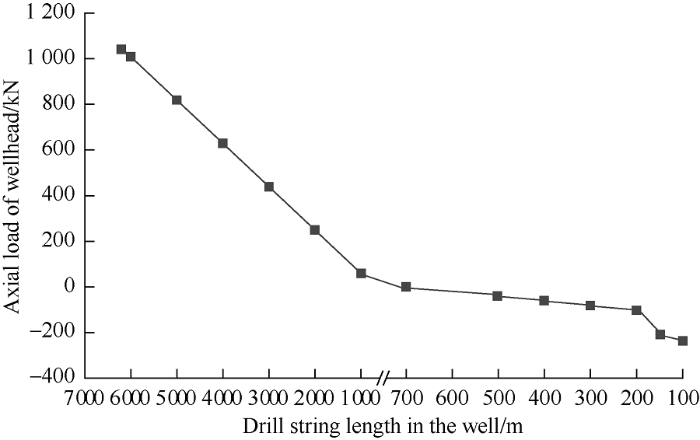
Since there is a maximum value of the shut-in casing pressure, there will be a critical drill string length under a certain working condition, that is, when the length of the drill string in the well exceeds the critical drill string length, there is no risk of uplift of the drill string. Under the maximum casing pressure, the relationship between the axial load of wellhead and the length of drill string in the well is shown in Fig. 5.
Fig. 5.
Fig. 5.
Relationship between axial load of wellhead and length of drill string.
Fig. 5 shows that the axial load at the wellhead is zero when the drill string length is reduced to 690 m. Afterward, the axial load direction of the wellhead turns from downward to upward, and the drill string pushes up. When the uplift force exceeds the blowout preventer sealing friction, the drill string would be pushed out of the wellhead. Therefore, under the condition of this example, the critical length of the drill string is 690 m, if the length of the drill string assembly is more than 690 m, there is no risk of drill string uplift; otherwise, it is necessary to analyze the critical shut-in time under the condition of this example.
3.3. The critical shut-in time of drill string uplift
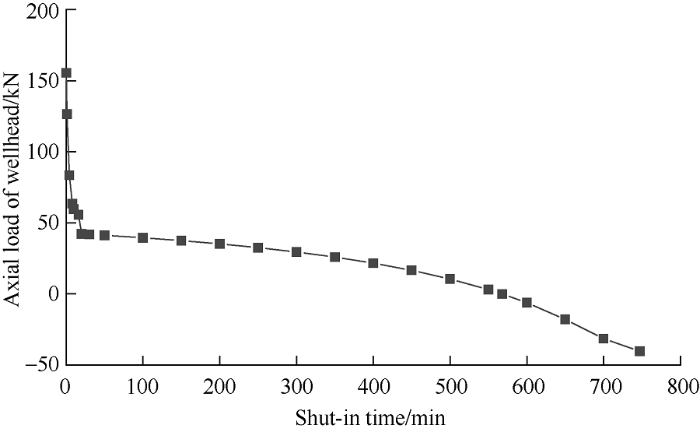
Fig. 6 shows the relationship between wellbore axial load and shut in time in the case of drill string length of 500 m. When the well is closed for 568 min, the axial load of the wellhead is zero, and then the direction of the axial load of the wellhead changes from downward to upward, and the drill string uplift occurs. In view of the overflow condition and the length of drill string of 500 m in this example, in order to prevent the drill string from uplift, the shut-in time should be controlled at less than 568 minutes, that is, the critical shut-in time is 568 min.
Fig. 6.
Fig. 6.
Relationship between wellhead axial load and shut-in time.
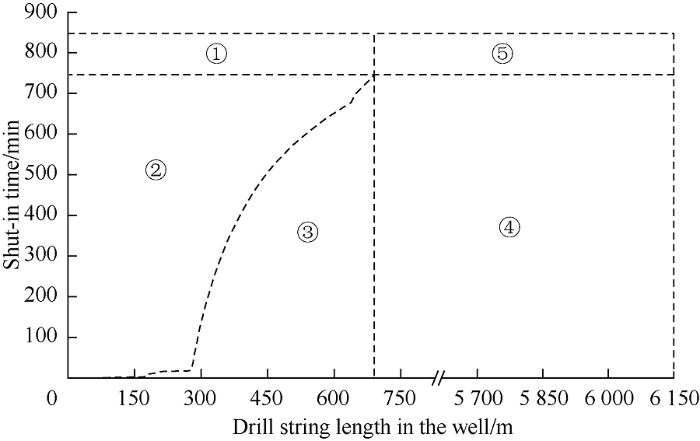
3.4. Risk distribution chart of drill string uplift
By calculating the critical shut-in time at different drill string lengths, the risk distribution map of drill string uplift can be obtained (Fig. 7). According to the critical shut-in time and critical drill string length, the risk of drill string uplift can be divided into five regions. The axial loads of inner wellhead are negative in regions ① and ② and there is a risk of drill string uplift; the axial loads of inner wellhead are positive in regions ③, ④ and ⑤, and there is no risk of drill string uplift. The lengths of drill string in regions ④ and ⑤ are larger than the critical drill string length. Gas has risen to the wellhead in regions ① and ②, casing pressure remains constant at the maximum, while gas still migrates in the wellbore in regions ③, ④ and ⑤, the casing pressure continues to rise. In order to reduce the risk of the drill string uplift, the length of drill string and the shut-in time in the well should be controlled within regions ③, ④ and ⑤.
Fig. 7.
Fig. 7.
Risk distribution map of drill string uplift.
4. Management program for preventing the uplift of drill string
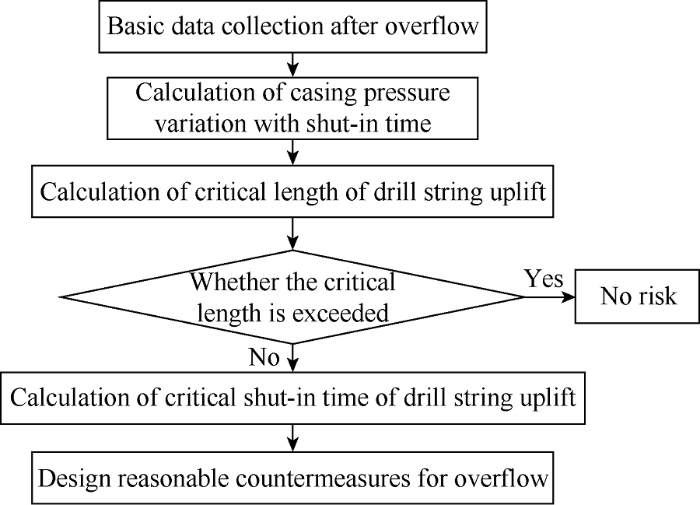
The risk of drill string uplift could occur during overflow well shut-in in ultra-deep wells. The shorter the drill string length is, the greater the risk. The longer the shut-in time, the greater the risk. Especially when the overflow occurs during the trip process, it is necessary to strictly prevent the uplift of drill string. Fig. 8 shows a set of management procedure for preventing drill string from uplift in ultra-deep wells, which can control drill string uplift risk more rigorously and scientifically.
Fig. 8.
Fig. 8.
Management program for preventing the uplift of drill string.
5. Conclusions
The source of drill string uplift force is the virtual force produced by hydrostatic force in the well. When the virtual force direction is opposite to the gravity direction, it is the drill string uplift force. When the uplift force is greater than the buoyant weight of drill string, the uplift of drill string would appear.
There are two key parameters: the critical drill string length and critical shut-in time. When the drill string length in the wellbore is less than the critical drill string length and the shut-in time exceeds the critical shut-in time, there is the risk of drill string uplift. On this basis, the risk distribution chart of drill string uplift can be plotted, and the length of drill string in the well and the shut-in time can be controlled in the risk-free zone to prevent drill string uplift.
A set of drill string uplift risk management program after well shut-in caused by overflow in ultra-deep wells is recommended to make the management of drill string uplift risk more rigorous and scientific.
Nomenclature
Aa(t,z)—annular cross-sectional area, m2;
Aai, Aao—inner and outer cross-sectional area of drill string, m2;
Ac(k)—filter area of mud cake in open hole section, m²;
Bg—gas volume factor, dimensionless;
Cg, Cl—isothermal compressibility of gas and drilling fluid, MPa-1;
dc, dt—outer and inner diameter of annulus, m;
Eg(t,z)—gas holdup of gas-liquid two-phase segment, %;
f1, f2—upward and downward hydraulic pressure on the first section of drill string, N;
f3—the downward hydraulic pressure on the second section of drill string, N;
fsc, fsm—solid content of mud cake and drilling fluid, %;
Fx—virtual force, N;
g—acceleration of gravity, 9.8 m/s2;
hg(t,z)—length of gas-liquid two-phase segment, m;
hlow(t)—length of drilling fluid column at the lower end of gas-liquid two-phase segment, m;
hr—thickness of gas layer, m;
Ha—well depth at section a, m;
Hi—well depth at the bottom of i-th section of drill string, m;
ΔHi—length of the i-th section drill string, m;
k—grid number of open hole segment;
K—mesh quantity of open hole segment;
Kc—mud cake permeability, μm²;
Ki—buoyancy coefficient of i-th drill string, dimensionless;
Kr—permeability of gas reservoir, 10-3 μm²;
mg(z)—gas mass in gas-liquid two-phase segment, kg;
n—number of drill strings;
p(t,z)—pressure of gas-liquid two-phase segment, MPa;
pai, pao—internal and external pressure of drill string, Pa;
pc—casing pressureat wellhead, Pa;
pc(t,k), pe(k)—wellbore and formation pressure in open hole section, MPa;
pe—supply pressure, MPa;
pw—bottom hole pressure, MPa;
pw0—bottom hole pressure at initial moment, MPa;
px(t)—pressure at x position in wellbore, MPa;
qi—unit weight of i-th section drill string, N/m;
Qg—gas flow rate, m³/min;
re—supply boundary, m;
ri, Ri—inner and outer radius of i-th section drill string, m;
rw—borehole radius, m;
t—time, min;
Δt—time step, min;
T—formation temperature, K;
Ta—true axial force at section a, N;
Te—effective axial force, N;
v—gas slippage velocity, m/s;
v1(t,z), v2(t,z)—gas slippage velocity at upper and lower ends of gas-liquid two-phase segment, m/s;
Vf(t)—filtrate loss of drilling fluid in unit time step, m3;
Vl—drilling fluid volume in well, m3;
Vlx(t)—drilling fluid unit volume in wellbore, m3;
Vg—overflow volume, m3;
ΔVg—the increase volume of gas due to expansion in unit time during slippage rise, m3;
Wi—mass of i-th section drill string, kg;
x—grid number of wellbore annulus;
X—grid quantity in wellbore annulus;
z—grid number of gas-liquid two-phase segment;
Z—grid quantity of gas-liquid two-phase segment;
Zg—natural gas compressibility factor, dimensionless;
μ—gas viscosity, mPa·s;
μm—drilling fluid viscosity, mPa·s;
ρg(t,z)—gas density in gas-liquid two-phase segment unit, kg/m3;
ρi, ρo—drilling fluid density inside and outside drillstring, kg/m3;
ρs—drill string density, kg/m3;
σ(t,z)—surface tension of gas-liquid, 10-3 N/m.
Reference
The research and design on the system of preventive drilling tool anti top
Technology of drilling bridge plug in high pressure gas well.
Study on snubbing unit used for top drive rig
The snubbing unit is a key equipment of the whole process underbalanced drilling,however,the installation and takedown of the equipment are complex,and operation time is long. In order to simplify operating procedure and improve the efficiency of snubbing unit,a new type of snubbing unit with built- in anti- gravity top features on top drive rig was designed. The snubbing unit was installed above the RCH. It could prevent upward force relying on the weight of the top drive in the process of snubbing,and the fixed kava of the snubbing unit in the process of make and break rotary. The two processes were used alternately to achieve the snubbing. By numerical simulation and laboratory experiments,the results showed that the device resistance reaches 15 tons on the top edge,under the condition of wellhead pressures 5MPa,the buckling failure of drilling tool wasn't occurred,the performance was safe and reliable. The developed snubbing unit used for top drive rig has a good application prospects in the whole process underbalanced drilling.
Study on axial force calculation and strength check of drill string in vertical holes
Analysis of buoyant force and calculation of axial force of drill string
Actual axial forces are devided into two parts in this paper. One part is the pressure which equals liquid column pressure applied on drill string section at the same depth, the other part is the effective axial force which equals effective bending axial force of drill string. For solving the actual axial forces of drill string, effective axial force is solved firstly and then actual axial force is converted. This paper defines neutral section and neutral point respectively with effective axial force and actual axial force.
Buckling of pipe under hydraulic pressure
The neutral zones in drill pipe and casing and their significance in relation to buckling and collapse.
Discussion on effects of internal and external pressure on axial force and stability of pipe string in oil wells
Reference[1]raised objection to the traditional theory of determining pipe stability established by A.Lubinski and H.B.Woods etc,and reached the conclusion that the determining method and formulas of traditional theory were improper.Looking into reference[1]carefully,the author found that some wordings of reference[1]are inconsistent with the historical facts and it has some misunderstandings to the traditional theory,the actual model proposed in it is not real enough,and an apparent error exists in the derivation,i.e.the pressure force on the lower end face of the tube has not been included in calculating the axial force.After analyzing the historical development process of the traditional theory,the paper confirms the correctness of the traditional theory and its application,and analyzes the apparent error in the derivation of reference[1].It is concluded that the denying of fictitious force,Woods Model,traditional method and formulas for calculating stability of pipe string in oil wells does not hold water.Not recognizing the existence of fictitious force in reference[1],the hydraulic pressure on the lower end of the pipe would not be nable to be handled correctly,that is the root cause of error in its derivation process.
Analysis on the pressure build-up and its recording time after shut-in
DOI:10.7623/syxb200205023
URL
[Cited within: 1]

The pressure build_up principle after shut_in is analyzed.The relationship between slippage and ascendance of gas in annulus as well as varies of stand pressure and case pressure in the well controlling process are described.On the basis of theory of gas reservoir engineering,the build_up characteristics of pressure after shut_in are discussed.A method for acquiring shut_in pressure of reservoirs with different permeabilities is proposed.
Wellbore flow analysis of continuous gas invasion during shut-in
Due to the effect of wellbore storage,shut-in period allows additional inflow of gas bubbles into the annulus.Wellbore and casing pressure increase with increase in shutin time as a consequence of gas upward migration,which will threaten the safety of well control.Therefore,the variation laws of surface and wellbore pressures which are caused by upward gas migration and gas compressibility at well shut-in should be investigated.Based on wellbore storage effect,a new model to the wellbore and casing pressure build-up during shut-in for a gas kick well is developed in this paper.Simulation results show that at different gas kick volumes,the rate of bottom-hole pressure rise increases as the permeability decreases.And surface casing pressure stabilizes quickly for low permeable formations.However,at equal initial annular gaseous volume,the rates of rise of the bottom-hole and surface casing pressures for low permeable formations are slower than for high permeability formations.
Characteristics of wellbore pressure change during shut-in after blowout
A new physical simulation system of drilling mud invasion in formation module
DOI:10.1016/S1876-3804(17)30016-2
URL
[Cited within: 1]

After several key technologies, including the saturation and pressurization of large sample, design of invasion room, sealing and pressure maintaining of the apparatus, and dynamic monitoring of the entire invasion process were solved, a multifunctional physical simulation system of drilling mud invasion in formation module has been designed and built. By using the system, the variation patterns of formation module resistivity, pressure and mud cake parameters during the invasion are summarized. The design idea, components, and functions of each component of the system are introduced in this paper; and a drilling mud invasion experiment in the sandstone formation module was done. The experiment results show that the radial resistivity of formation module decreases in turn during brine drilling mud invasion; at the beginning of invasion, the mud cake is gradually formed with the increase of its thickness and the decrease of its porosity and permeability, and the radial pressure gradient of formation module decreases rapidly; in the middle and late periods of invasion, the mud cake properties and the radial pressure gradient of formation module become stable. The designed system, with high simulation degree, high utilization ratio and good maneuverability, can be used to reveal the invasion mechanism of drilling mud in sandstone reservoirs, analyze invasion characteristics, and improve invasion correction method for logging response and other researches.
Experimental tests for gas kick migration analysis.