Introduction
At the late stage of fractured reservoirs production cycle, the hydrocarbon could no longer be recovered by the original pressure build-up, then waterflooding is popularly used to enhance the recovery of hydrocarbons[1,2]. In homogeneous reservoirs, the waterflooding will reduce the original residual oil in the rock, but in most cases, this ideal scenario is rare to occur. One important factor is the reservoir heterogeneity and the other key factor, which has even more impact on the recovery efficiency, is the pre-existence of natural fractures. For waterflooding in fractured reservoirs, high-permeable fracture is conjectured to act as a fast channel. In the worst scenario, most of the water will only run through fractures and does not displace oil from the matrix blocks. The sweep efficiency will be limited, so as the recovery factor. The recovery of oil from fractured reservoirs is controlled by the interaction between brine/oil/rock interaction, which depends on the rock wettability and two-phase flow, the chemical and physical properties of all of the three components, fracture geometry, fracture permeability/conductivity[3,4,5,6,7]. Waterflooding in fractured reservoirs has attracted a lot of attention in the past decades[8,9].
Conventional simulation methods of modeling fractured reservoirs include analytical methods, semi-analytical methods[10,11] and numerical methods[12]. The dual-porosity or dual permeability model[13,14] is widely used in numerical simulations of fractured reservoirs, but the model is mostly over- simplified compared to the actual field complexities. To that respective, discrete-fracture models, using finite-volume or finite-difference methods, have been developed. To be compatible with the complex geometries of fractures such as nonplanar fractures and fractures with variable aperture, reservoir simulators using unstructured grids have also been developed[15]. However, the use of unstructured grids often leads to high computational cost so that it is only used in limited application in real field studies. As a solution, a technique that directly incorporates complex fractures in a conventional structured grid was developed, which was named as Embedded Discrete Fracture Model (EDFM)[16], and the EDFM was further developed for 3D reservoir simulation[17]. Recently, the EDFM has been widely used for naturally and hydraulically fractured reservoirs[18,19].
Using the EDFM method, the reservoir pressure distribution and fluxes could be accurately simulated, but in fractured reservoirs with complex fracture networks, pressure distribution cannot describe the complexity of the fracture network and fluid flow trajectories. In order to quantify the different waterflooding scenarios and better manage the waterflooding performance, the explicit fluid flow trajectory and water travel time need to be computed for determining which waterflooding approach is the best for a certain reservoir. To understand and appraise waterflooding recovery efficiency in finer scale, the streamline simulation which quantitatively computes the flow trajectories and travel time[20,21,22,23] is used. Previously, streamline simulation method has been frequently used to waterflooding in fractured reservoirs[24,25], but because of the limitations of dual-porosity or dual-permeability method they used to simulate the fractures, they could not capture the fracture geometry and simulate the flux results as accurately as the EDFM method.
In this study, we develop a new numerical model fully integrating EDFM and streamline methods for waterflooding in naturally fractured reservoirs. To the best of authors’ knowledge, this is the first time that a study has performed streamline simulation for fractured reservoirs using the EDFM method, which can produce streamline trajectories in matrix and fractures with a higher resolution than the traditional dual-continuum methods.
1. Mathematical reservoir model
1.1. EDFM in black-oil model
Black-oil equations have been widely used for modeling three phase fluid flow in petroleum reservoirs. It is suitable to simulate the waterflooding scenario in fractured reservoirs using EDFM approach due to the feasibility of EDFM in modeling the exact geometry of fractures[18]. Modeling complex fracture geometries has shown to be manageable with the use of the EDFM approach[19]. By discretizing fractures into interconnected small fracture segments and adding them to the computational domain, the EDFM is able to combine traits from both dual-continuum models and discrete fracture models. Hence, the EDFM approach is capable of avoiding the high-computational demand of unstructured gridding while keeping the unique functionality of the simulator in use.
1.2. Streamline simulation methodology
Streamline simulation has been widely used for flow trajectories visualization and travel time computation in fluid dynamics study especially in petroleum field. The early fundamental work of applying streamlines and streamtubes in fluid transport problems were developed by Muskat[21]. Subsequently, many researchers have used numerical streamtube methods to model simple flooding problems[26,27,28], where the authors described how to define potential functions and stream functions for incompressible flows in 2D space. Datta- Gupta and King first introduced the streamline “time of flight” as a spatial variable and was used to solve the transport equation (saturation) along the streamlines numerically[29]. Since then, streamline models have been applied to a broader range of problems and have gradually replaced streamtube models in practical applications. With the increasing complexity of the reservoir geometries, the streamline algorithms have also evolved, especially with the emerging of fracture modeling in unconventional reservoirs. The classical work of streamline trajectories and time of flight calculation was completed for rectangular cells[30], where the transit time from an initial point is accumulated cell by cell and the velocity is interpolated linearly within each cell. This method was generalized for more complicated 3D reservoir geometries by Cordes and Kinzelbach, where the corner-point geometry and fluid flux are mapped to a unit cube via an isoparametric transformation[31]. This construction was further simplified through the introduction of a pseudo time of flight in corner-point cells[32]. For streamline tracing problems within unstructured grids, faulted grids and grids with locally embedded, refined, or coarsened grids, the Local Boundary Layer method was applied to handle the velocity discontinuity issues across these boundaries[33,34,35].
For streamline simulation in naturally fractured reservoirs, there are two challenges. First, in the presence of fractures, streamline simulation needs to compute the streamline trajectories across interfaces with different resolutions on two sides. Second, after reservoir simulator calculates flow rate for matrix and fractures, streamline simulation requires more fluxes values than known ones, so that the unknown fluxes need to be reconstructed. For the first issue, the local boundary layer concept has been proposed to handle the flux discontinuity across these interfaces[32,33,34,35], and this technique will also be modified and applied in this study. In fact, the cases studied here are very similar to the Local Grid Refinement (LGR) cases illustrated in previous references, because the side with fractures is the finer grid and the other side is the parent grid. The difference is that the LGR cases do not need extra grid construction for cells with fractures. But for fractures, the cell geometry and fracture geometry are given separately so that we need to calculate their intersections to construct the new geometry. For the second issue, based on proper assumptions and mass balance equations, all six volumetric flow rates of each cell will be reconstructed using the total flux from matrix to fracture cells calculated by the EDFM.
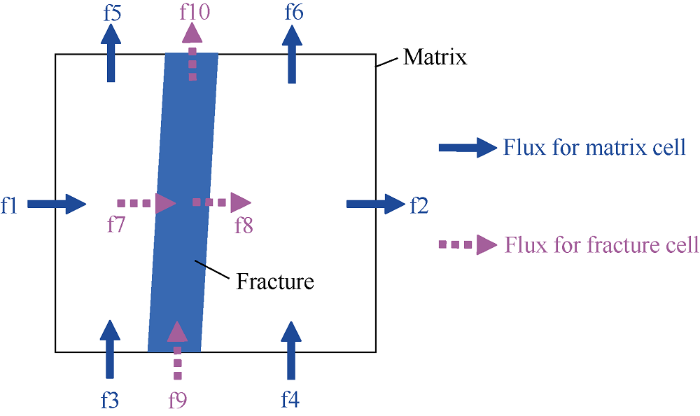
Fig. 1 illustrated the volumetric flow rates relations for a 2D matrix cell intersecting with just one fracture. The original matrix cell (with black sides) is divided by the fracture (in blue) into two child matrix cells, which have fluxes f1-f6, and the fracture cell has fluxes f7-f10. Fluxes f7 and f8 are shared between the matrix cell and the fracture cell. Suppose f3+ f4+f9=F1, f5+f6+f10=F2, and f7+f8=F3, and the reservoir simulator with EDFM method will compute the following fluxes for matrix cells, the flux on each face of the matrix cell, f1, f2, F1 and F2, and the fluxes of the facture cell, f9 and f10. The total flux transfer between matrix and fracture, F3, will also be computed by the EDFM method. But for streamline simulation, all fluxes for each face of each new cell should be known, so that the fluxes need to be reconstructed.
Fig. 1.
Fig. 1.
Reconstruction of the fracture-matrix interaction fluxes on a 2-D cell.
In all the cases studied in this work, on the bottom face, f9 shares most part of the flux on that face, so it is proper to make the following assumption: f3=f4. The same assumptions could be obtained for f5=f6. Combining all the mass balances equations to return the following:
In equation (1), since variables F1, f1, f2, f9, f10 are all known, we can compute variables f3 and f4 directly as ${{f}_{3}}={{f}_{4}}=$ $\frac{1}{2}({{F}_{1}}-{{f}_{9}})$, and rewrite equation (1) as the following form,
Rewrite it in the linear form,
where
$A=\left( \begin{matrix} 1 & 0 & 1 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \\ \end{matrix} \right)$, $\overset{\to }{\mathop{f}}\,=\left( \begin{matrix} {{f}_{5}} \\ {{f}_{6}} \\ {{f}_{7}} \\ {{f}_{8}} \\ \end{matrix} \right)$, and$\overset{\to }{\mathop{F}}\,=\left( \begin{matrix} {{f}_{1}}+{{f}_{3}} \\ 0 \\ -{{f}_{2}}+{{f}_{4}} \\ {{f}_{10}}-{{f}_{9}} \\ \end{matrix} \right)$
Solving equation (3), all the fluxes needed for streamline tracing and time of flight calculation could be reconstructed and stored for each fracture cell and matrix cell, before streamline simulation is used to trace the streamlines.
For well cell intersecting with fractures, after the flow rate of the well cell is computed, the streamline tracing algorithm will treat the well cell as the same with other cells.
2. Model application
2.1. Model assumptions
In this study, the reservoir is naturally fractured and has one injector at the southwest corner and one producer at the northeast corner. To focus on essential mechanism of fluid flow in natural fractures and to avoid the extra complexity of unstructured geometries caused by irregular intersections between fractures and matrix cells, the natural fractures are assumed to have no intersections with each other and the strike angles of all fractures are either 0 degree or 90 degree. And the fractures have no intersection with the edge of the grid. The flow is incompressible and follows Darcy's law, and fracture and matrix have their own permeability, porosity and relativity permeability. The fracture permeability is assumed to have large contrast with matrix permeability. The focus of this study is on the water flow trajectories and travel time in fractured reservoirs.
2.2. Model description
For all of the synthetic cases designed in this study, a reservoir model of 152.4 m×152.4 m×6.1 m is constructed. The model is discretized uniformly by 20×20×1 grid blocks, which leads to 400 grid blocks with each block of dimension 7.62 m×7.62 m×6.10 m. Water is injected at a constant rate, 0.00018 m3/s and the producer has a fixed pressure at 6.89 MPa. Table 1 listed all basic reservoir, fluid and fracture properties, which will be used in the following case studies.
Table 1 Basic reservoir and fracture parameters used for reservoir model.
| Parameter | Symbol | SI Unit | Value |
|---|---|---|---|
| Injector flow rate | Q | m3/s | 0.00018 |
| Reservoir temperature | T | K | 288.706 |
| Reservoir permeability | Ki | m2 | 1.97×10-14 |
| Reservoir thickness | h | m | 6.10 |
| Reservoir porosity | ϕ | - | 10% |
| Oil viscosity | μ | Pa∙s | 0.001125 |
| Oil density | ρ | kg/m3 | 784.5 |
| Fracture height | hf | m | 6.10 |
2.3. Model validation and efficiency
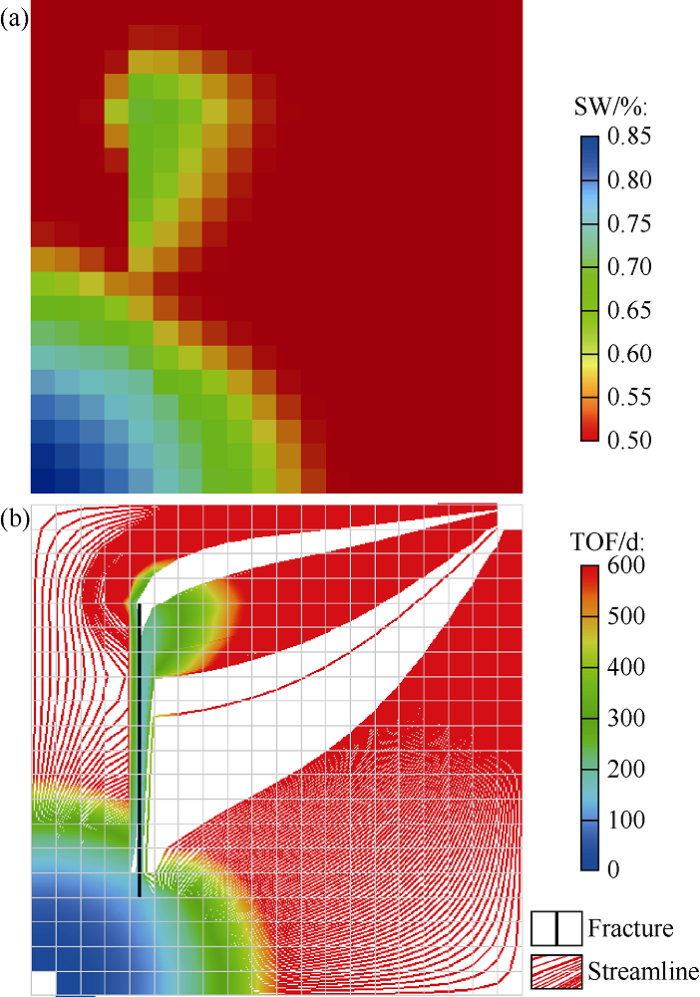
To show the accuracy of streamline simulation based on the EDFM method, the streamline trajectories and TOF profile are compared with water saturation profile. Fig. 2 shows that after 600 days of production, the water saturation profile in Fig. 2(a) is consistent with the streamline trajectories and TOF profile plotted in Fig. 2(b).
Fig. 2.
Fig. 2.
Comparison between water saturation profile and time of flight profile after 600 days. (a) Water saturation profile; (b) Streamline and TOF.
After constructing the fracture geometry and the neighborhood relations, the streamline tracing algorithm runs each streamline one by one independently, so that it is very convenient for potential parallel computation implementation. In this case, the computation time of streamline simulation will mostly be determined by the cell numbers in each model. With the introduction of extra fracture cells, the computation time will increase correspondingly. For the case shown in Fig. 2, the CPU time for case running is about 75 seconds and the streamline computation time takes approximately 240 seconds. For the corresponding case without the fracture, the CPU time for case running is about 120 seconds and the streamline computation time takes approximately 300 seconds. Thus the addition of extra fracture cells could in fact increase the computation cost but the overall efficiency is still good enough considering the resolution this method could achieve.
2.4. Case studies
2.4.1. Base case: homogeneous reservoir without fractures
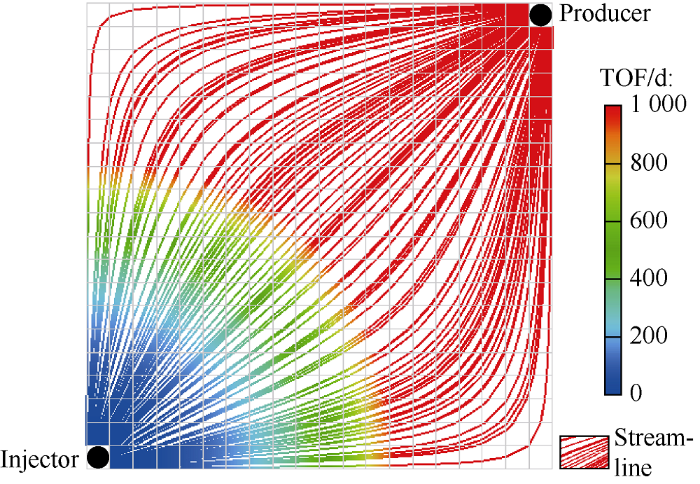
The first case is the homogeneous reservoir model without any natural fractures. Our streamline simulation results, including the red streamline trajectories and rainbow color time of flight values, are illustrated in Fig. 3. From this base case, the waterflooding displacement profile could be clearly visualized. Because the reservoir is homogeneous, the waterfront moves forward radially.
Fig. 3.
Fig. 3.
Streamline and TOF results for the base case.
2.4.2. Effect of fracture conductivity
To investigate the impact of fracture conductivity on flow trajectories and time of flight values, single vertical fracture with high conductivity (Case 1) and single vertical fracture with low conductivity (Case 2) are designed with different fracture conductivities.
In Case 1, there is one vertical fracture with length 83.8 m on the left side of the reservoir, the fracture conductivity is 7.52×10-9 m2∙m. The streamline and TOF results are plotted in Fig. 4a.
Fig. 4.
Fig. 4.
Streamline and TOF results for Case 1 and Case 2 with different fracture conductivities. (a) Streamline profile and TOF results for fracture conductivity Fcd=7.52×10-9 m2∙m; (b) Streamline profile and TOF results for fracture conductivity Fcd=7.52×10-11 m2∙m.
Fig. 4a shows that before the waterfront reaches the natural fracture, it runs radially uniform. Once the waterfront arrives at the natural fracture, its velocity increases quickly so that the water runs through the fracture much faster than in the matrix. By 1000 days, the water passing through the natural fractures has already arrived close to the producer well, while the water flowing in the matrix has just moved to a short distance away from the injector well (118 m).
While the natural fracture acts as the fast channel for some of the fluids, it also acts as a “barrier” to block those fluids so that the fluids could only travel within the fracture region and not reach a wider region. Comparing with Fig. 3, Fig. 4a has a larger blank region on the right of the vertical fracture that does not have streamline at all. This blank region is the so-called “dead zone” or “choke zone”, which will impact the total swept volume and consequently lower down the oil recovery factor. To avoid early water breakthrough, some approaches such as injecting gels or nanoparticles could be used to delay the fast flowing of the water in the natural fractures and the “barrier” effect of the high permeable fractures.
In Case 2, all other properties are the same as Case 1, but the fracture conductivity decreases to 7.52×10-11 m2∙m. The results are plotted in Fig. 4b. With fracture conductivity of 7.52×10-9 m2∙m, at t=1000 days, Fig. 4a shows that the waterfront has arrived at a location 38.1 m far away from the top of the fracture, while with conductivity drops to 7.52× 10-11 m2∙m, the waterfront travels to just 15.2 m far away from the top of the fracture. With the fracture conductivity decreasing, the “fast channel” and “barrier” effect of the fracture get less significant. As the fracture conductivity decreases, we see that more and more water is going through the fracture, and the “barrier” effect such as the deviations of the flow trajectories gets smaller. Less “dead zone” is created, as the fracture conductivity gets smaller.
2.4.3. Effect of the number of fractures
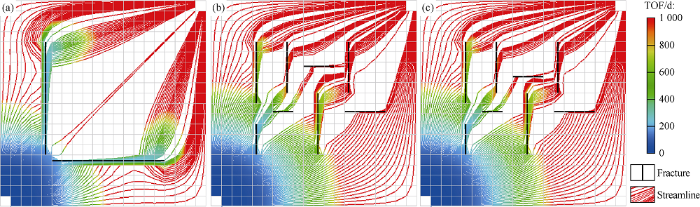
Another important property to investigate is the number of natural fractures. To study the impact of fracture numbers on waterflooding performance, 3 vertical fractures (Case 3) and 12 vertical fractures (Case 4) are designed with different number of natural fractures.
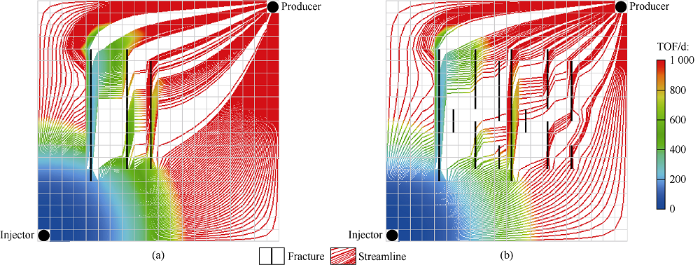
Case 3 is designed based on Case 1. The first vertical fracture from the left is the same with Case 1, but there are two more vertical fractures, with lengths 76.2 m and 68.6 m, on the right side of the first fracture. The streamline trajectories, TOF profiles are given in Fig. 5a.
Fig. 5.
Fig. 5.
Waterflooding results of Case 3 and Case 4. (a) Streamline profile and TOF results for Case 3; (b) Streamline profile and TOF results for Case 4.
Different with Case 1, we see that after the flow trajectories of most the water flow invading upwards were altered by the first vertical fracture, the rest of the fluid flow will advance across the first vertical fracture but then altered by the second vertical fracture. The effect of the second fracture is less than the first fracture for affecting the flow trajectorie, as more portion of the streamlines will run across the second fracture after running only a short distance inside the fracture. But the fast channel effect could still be clearly seen as the streamline change advancing directions abruptly once it reaches the reigon close to the fractures. The third vertical fracture shows similar “fast channel” effect but with even less impact than the second vertical fracture.
In Case 4, there are 12 vertical fractures, which have same conductivity but different lengths, varying from 15.2 m to 83.8 m. The corresponding streamline trajectories and TOF values are plotted in Fig. 5b. Some interesting results could be observed from this case. First, the same “fast channel” effect shown in Case 3 is also seen here, but for fractures with different distances from the injector well, the impacts of fractures become less obvious, as we discussed for Case 3 in Section 3.4.4. Second, and more interestingly, the second vertical fracture has little impact on the streamline trajectories because of its limited length. Comparing the fractures with huge differences in lengths, it is clear that shorter fractures has less impact on the streamline trajectories and TOF than the longer fractures, as we see the “fast channel” effect of the streamline directions and the “barrier” effect are getting less obvious for shorter fractures.
2.4.4. Effect of fracture locations
The next cases are used to illustrate the effects of fracture locations, in which the fractures will have same properties but different orientations and locations.
Case 5 has two fractures, with one vertical fracture having length 83.8 m and another horizontal fracture having the same length 83.8 m. These two fractures have the same properties, such as height, aperture, and fracture conductivity, as listed in Table 1. Their orientations are symmetric with respect to the diagonal of the reservoir. The corresponding streamline trajectories, and TOF results are shown in Fig. 6a.
Fig. 6.
Fig. 6.
Waterflooding results for Cases 5, 6 and 7. (a) Streamline profile and TOF result of Case 5; (a) Streamline profile and TOF result of Case 6; (a) Streamline profile and TOF result of Case 7.
Since the second fracture has the same properties with the first fracture, it shows the same flow behavior as the fast channel, which leads to faster breakthrough of the water compared to the waterflooding in the matrix. Fig. 6a shows that after 1000 days, the waterfront has already advanced through the fractures and run even further, while in the zones far away from the fractures, the waterfront is still in the zone very close to the injector well. Fig. 6a also illustrates the exact symmetry for the streamline trajectories and time of flight profiles because of the symmetry of the two fractures. There is again a dead zone generated due to the presence of these two natural fractures. The water advancing from the injector well is “blocked” by these two fractures and flows along the fractures so that the central part of the reservoir is poorly waterflooded.
There are 8 fractures in Case 6. The streamline simulation results of Case 6 are shown in Fig. 6b. Different with Case 4, the first long vertical fracture on the left side was replaced with two short vertical fractures. This change immediately causes big differences in streamline trajectories, from which it can be seen that more water runs past the first vertical fracture line. Second, the extra 3 horizontal fractures help the faster arrival of waterfront to the producer, while in Case 4 all vertical fractures act as “barriers” in terms of water breakthrough. The detailed analysis of these changes is given in the Discussion part below.
Case 7 has the top horizontal fracture 9.1 m lower than in Case 6. The results are plotted in Fig. 6c. The effect of single fracture’s location is clear. The top horizontal fracture acts as the “fast channel” but could also be interpreted as a “barrier” to the area above it. With the existence of this fracture, the waterfront could not flow to the area above this fracture, which caused a “dead zone”, where the oil could not be water flooded. In this case, because of the lower location of the top horizontal fracture, the dead zone area gets larger than Case 6. The quantification and visualization of the dead zone could be used for optimizing well placement in the field.
2.5. Waterflooding performance evaluation
During the design of a waterflooding strategy, there are two major factors to consider, the water breakthrough time and the water swept volume. Previously, the water breakthrough time could be estimated from checking the water production data to find the time when water production is suddenly increased. The water swept area could be estimated by checking the pressure or water saturation map to see how many cells are affected by the variations, but usually the change is minor so that it is hard to tell where the changes happen.
Now with the streamline technique verified by Fig. 2, water breakthrough time can be calculated by taking the minimum total TOF value among all streamlines arriving at the producer well. It could be directly calculated by comparing all the total TOF values for all streamlines. This method is more accurate. It should be mentioned that the swept volume was calculated approximately by summing up all the cell volumes where at least one streamline passes. In this study, swept cells number is used instead of the exact swept volume because all cells have the same cell volume. Multiplying swept cells with the volume of each cell, we can obtain the actual swept volume. Swept efficiency is the ration between the swept cells number divided and the total cell number.
Following the definitions of water breakthrough time and swept volume defined above, a post-processing workflow is designed to calculate the water breakthrough time and swept volume of all the cases we studied. Table 2 lists all the results of the water breakthrough time, swept volume and swept efficiency. By comparing all the cases of this study, many intriguing observations could be made.
Table 2 Summary of water breakthrough time and swept volume of all cases.
| Case number | Water breakthrough (day) | Swept cells | Swept efficiency |
|---|---|---|---|
| Base | 3912 | 400 | 100% |
| 1 | 2169 | 348 | 87% |
| 2 | 3532 | 400 | 100% |
| 3 | 2608 | 378 | 94.5% |
| 4 | 2387 | 376 | 94% |
| 5 | 2259 | 324 | 81% |
| 6 | 2056 | 375 | 93.75% |
| 7 | 2047 | 370 | 92.5% |
With the same reservoir setting, the reservoirs with fractures will have faster water breakthrough and less swept volume. This is clearly seen from the comparison between the base case and Case 1-7. With higher fracture conductivity in Case 1, the water breakthrough is vastly fastened by 45%, and the swept efficiency is decreased by 13%. Although one single natural fracture always fastens the water breakthrough and decreases the swept volume, having more fractures could lead to different outcomes. Case 5 and Case 1 show that the water breakthrough is slowed down from 2169 days to 2259 days, but the swept volume decreased from 348 cells to 324 cells (7% decreased). On the other hand, Case 1 has two more vertical fractures than Case 3, and the water breakthrough is slowed by 20% and the swept volume is also increased by 9%. This suggests that more vertical fractures will likely have better waterflooding performance than one more horizontal fracture.
Although two more vertical fractures of Case 3 than Case 1 could prolong the water breakthrough time and increase the swept area, it does not mean more vertical fractures could be better. Case 4 has 12 vertical fractures and the total fracture length is much larger than Case 3, but the water breakthrough time is even faster than Case 3 (8% faster), while the total swept volume is similar.
Multiple sets of fractures with different orientations could effectively speed up the water breakthrough. Case 6 and Case 7 have 8 fractures of less total length than Case 4, but the water breakthrough time of Case 4 is 17% faster than Case 6 and 7, while the total swept volume is similar.
Last but not least, the locations of fractures impact a lot on the swept volume. The only difference between Case 7 and Case 6 is the location of the top horizontal fracture, while the swept volume of Case 7 is decreased by 1%. This difference should not be overlooked because this is caused by a slight difference in the location of just one short horizontal fracture. Practically, there will be many more fractures involved.
3. Discussion
The modeling of waterflooding performance in naturally fractured reservoirs is important for engineers to understand the fluid mechanism of fluid flow in fractures and evaluate different waterflooding plans to achieve the best economic performance. Due to the complexity of fracture modelling, there are only limited works done about waterflooding simulation in fractured reservoirs. Most of the existing studies have used the classical dual-porosity/dual-permeability model to simulate the natural fractures, which could lead to results with low resolution and accuracy due to the limitations of dual-porosity/dual permeability models.
Combining the capacity explicit modeling of the natural fractures in EDFM and quantitative visualization of streamline trajectories and TOF, this study investigated the waterflooding performance in naturally fractured reservoirs, by computing waterfront travel paths and running time accurately and quantitatively, in terms of fracture properties, fractures number and fracture locations. In this study, all the fractures are set to be simple so that we can see the essential yet dramatic differences even one fracture could make for the waterflooding swept volume and water breakthrough. In the future, this novel technique could be extended to assist petroleum engineers to optimize the injection rates and infilling well locations in waterflooding production plan.
In this study, all cases are 2D synthetic cases so that gravity effect is not considered. The time dependence is ignored too because we focus on the streamline trajectories at one instant time. For practical 3D cases with complex fractures, the gravity effect and the time dependency of streamline trajectory should be considered and investigated in our future studies. On the other hand, the natural fractures are constructed synthetically in this study, and if more data are available for natural fracture characterization, practical natural fracture networks could be built and applied in actual field cases. In real field cases, fractures will have more complicated geometries, orientations and intersections, so that the technique proposed in this study needs to be further extended and generalized.
4. Conclusions
Under the same setting, the water breakthrough time and the swept efficiency for the reservoirs with natural fractures is around 30% faster and 10% lower than the reservoirs without natural fractures in this case study, respectively. While one single high permeable fracture always shortens the water breakthrough time and decreases the swept efficiency, more fractures could lead to different results, depending on the properties and complexity of fractures. The differences could be 20% for the water breakthrough time and 9% for the swept efficiency for different fracture geometries investigated in this study. Shorter fractures have less impact on water trajectories than longer fractures, proportionally to the fracture length. The location of fractures significantly affects the swept efficiency. The different location of one fracture could result in 1% swept efficiency difference.
Reference
Streamline- based production data integration in naturally fractured reservoirs
DOI:10.2118/89914-MS
URL
[Cited within: 1]

Streamline-based models have shown great potential in reconciling high resolution geologic models to production data. In this work we extend the streamline-based production data integration technique to naturally fractured reservoirs. We use a dualporosity streamline model for fracture flow simulation by treating the fracture and matrix as separate continua that are connected through a transfer function. Next, we analytically compute the sensitivities that define the relationship between the reservoir properties and the production response in fractured reservoirs. Finally, production data integration is carried out via the Generalized Travel Time inversion (GTT). We also apply the streamline-derived sensitivities in conjunction with a dual porosity finite difference simulator to combine the efficiency of the streamline approach with the versatility of the finite difference approach. This significantly broadens the applicability of the streamlinebased approach in terms of incorporating compressibility effects and complex physics. The number of reservoir parameters to be estimated is commonly orders of magnitude larger than the observation data, leading to non-uniqueness and uncertainty in reservoir parameter estimate. Such uncertainty is passed to reservoir response forecast which needs to be quantified in economic and operational risk analysis. In this work we sample parameter uncertainty using a new two-stage Markov Chain Monte Carlo (MCMC) that is very fast and overcomes much of its current limitations. The computational efficiency comes through a substantial increase in the acceptance rate during MCMC by using a fast linearized approximation to the flow simulation and the likelihood function, the critical link between the reservoir model and production data. The Gradual Deformation Method (GDM) provides a useful framework to preserve geologic structure. Current dynamic data integration methods using GDM are inefficient due to the use of numerical sensitivity calculations which limits the method to deforming two or three models at a time. In this work, we derived streamline-based analytical sensitivities for the GDM that can be obtained from a single simulation run for any number of basis models. The new Generalized Travel Time GDM (GTT-GDM) is highly efficient and achieved a performance close to regular GTT inversion while preserving the geologic structure.
Appraising carbon geological-stroage potential in unconventional reservoirs: Engineering-parameters analysis
A semianalytic approach to tracer flow modelling in heterogeneous permeable media
DOI:10.1016/0309-1708(94)00021-V
URL
[Cited within: 1]

A semianalytic approach for modeling tracer motion in heterogeneous permeable media is presented. The method is analytic along streamlines; the streamlines are derived from an underlying velocity field which is obtained numerically from a conventional fluid flow simulator. This generalizes the approach to any arbitrary configuration of wells and also to areally heterogeneous permeability fields. The semianalytic scheme is based on the observation that in a velocity field derived by finite difference, streamlines can be approximated by piecewise hyperbolic intervals. Along each of these intervals the evolution equation can be solved exactly. Thus, the approach is free from numerical time truncation error. Once tracer transit times to a producing well have been determined, the tracer response curve and the area swept by the tracer can be obtained from simple integral expressions. The transit time formalism allows for easy extension of the semianalytic approach to multiphase flow problems and the results are shown to be in excellent agreement with high resolution finite-difference simulations, but obtained at a fraction of the computation time. We have illustrated the semianalytic approach through application to tracer migration in homogeneous as well as heterogeneous quarter five spot patterns.
Streamline-based dual porosity simulation of fractured reservoirs
Two models for the waterflooding of naturally fractured reservoirs
A method for evaluation of water flooding performance in fractured reservoirs
DOI:10.1016/j.petrol.2014.06.002
URL
[Cited within: 1]

61A methodology is proposed to evaluate water-flooding in fractured reservoir.61A new revision imbibition model is proposed for the dynamic saturation profile.61The methodology is tested on laboratory data and applied to some field cases.61Compared against simulation and other classic methods, the result is reliable.
Micro- influencing mechanism of permeability on spontaneous imbibition recovery for tight sandstone reservoirs
DOI:10.1016/S1876-3804(17)30107-6
URL
[Cited within: 1]

The upper part of the 4 th member of Paleogene Shahejie Formation in Bonan sag, Bohai Bay Basin, East China was taken as the study object. Conventional core analysis, casting and conventional thin section inspection, scanning electron microscope observation, particle size analysis and fluid inclusion analysis were carried out on cores, and the data from these analyses and tests was used to find out the evolution of diagenetic environment of the saline lacustrine basin and the main factors controlling the deep formation of high quality reservoirs. The diagenetic environment of the saline lacustrine basin experienced alkali and acid alternation. In the early alkali diagenetic environment, large amounts of carbonate cement filled the primary pores, making the reservoir porosity reduce sharply from 37.3% to 18.77%, meanwhile, keeping the primary pores from compaction, and retaining the dissolution space. In the middle-late stage of acid diagenetic environment, early carbonate cement was dissolved, resulting in rise of reservoir porosity by 10.59%, and thus the formation of the deep high quality reservoirs. The distribution of high quality deep reservoirs is controlled by the development of gypsum salt rock, source rock, fracture system and sedimentary body distribution jointly. Deeply buried high quality reservoirs in the upper part of the 4 th member of the Shahejie Formation in Bonan sag are nearshore subaqueous fan-end sandstone and some fan-medium fine conglomerate buried at 3 400-4 400 m in the north steep slope.
Geometrical description and permeability calculation about shale tensile micro-fractures
DOI:10.1016/S1876-3804(16)30013-1 URL [Cited within: 1]
An improved rate-transient analysis model of multi-fractured horizontal wells with non-uniform hydraulic fracture properties
DOI:10.3390/en11020393 URL [Cited within: 1]
Compositional modeling of discrete-fractured media without transfer functions by the discontinuous galerkin and mixed methods
Full-field streamline tracing in complex faulted systems with non-neighbor connections
Analytical and numerical solution of oil recovery from fractured reservoirs with empirical transfer functions
Velocity interpolation and streamline tracing on irregular geometries
DOI:10.1007/s10596-011-9256-0
URL
[Cited within: 1]

Abstract(div) and (curl) valid on general grids that is based on barycentric coordinates and that reproduces uniform flow. The interpolation can be used to compute the streamline directly on the complex cell geometry. The method generalizes to convex polytopes in 3D, with a restriction on the polytope topology near corners that is shown to be satisfied by several popular grid types. Numerical results confirm that the method is applicable to general grids and preserves uniform flow.
Numerical solution of multiphase two-dimensional incompressible flow using streamtube relationships
Comparison of discrete-fracture and dual-permeability models for multiphase flow in naturally fractured reservoirs
Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs
DOI:10.2118/154246-PA URL [Cited within: 1]
High- resolution numerical modeling of complex and irregular fracture patterns in shale-gas reservoirs and tight gas reservoirs
Semi-analytical computation of path lines for finite-difference models
DOI:10.1111/j.1745-6584.1988.tb00425.x
URL
[Cited within: 1]

A semianalytical particle tracking method was developed for use with velocities generated from block centered finite-difference ground-water flow models. The method is based on the assumption that each directional velocity component varies linearly within a grid cell in its own coordinate directions. This assumption allows an analytical expression to be obtained describing the flow path within an individual grid cell. Given the initial position of a particle anywhere in a cell, the coordinates of any other point along its path line within the cell, and the time of travel between them, can be computed directly. For steady-state systems, the exit point for a particle entering a cell at any arbitrary location can be computed in a single step. By following the particle as it moves from cell to cell, this method can be used to trace the path of a particle through any multidimensional flow field generated from a block-centered finite-difference flow model.
Multistage interwell chemical tracing for step-by-step profile control of water channeling and flooding of fractured ultra-low permeability reservoirs
DOI:10.1016/S1876-3804(16)30079-9
URL
[Cited within: 1]

To monitor the dynamic variations of sweep area and formation parameters during the process of multiple slugs step-by-step profile control, the multistage interwell chemical tracing technique was proposed and tested in field, in line with the features of the step-by-step profile control in fractured ultra-low permeability reservoirs and the basic principle of chemical tracing test. According to the design scheme of step-by-step profile control and the characteristics of water channeling and flooding in fractured ultra-low permeability reservoirs, this study worked out times-design method for interwell tracing, optimized the selection principle of chemical tracer and calculation formula of tracer dosage, and set up the parameter optimization forecasting method of step-by-step profile control based on multistage interwell tracing. The application results of the method show multistage interwell chemical tracing can reflect dynamic variation of fractured parameters effectively, and the monitoring results match with the dynamic production testing results, demonstrating good adaptability of the method.
An embedded grid-free approach for near wellbore streamline simulation
The behavior of naturally fractured reservoirs
Efficient simulation for low-salinity waterflooding in porous and fractured reservoirs
Discrete-fracture modeling of complex hydraulic-fracture geometries in reservoir simulators
A comprehensive model for real gas transport in shale formations with complex non- planar fracture networks
DOI:10.1038/srep36673
URL
PMID:5098178
[Cited within: 1]

A complex fracture network is generally generated during the hydraulic fracturing treatment in shale gas reservoirs.
Robust streamline tracing using inter-cell fluxes in locally refined and unstructured grids
DOI:10.1029/2011WR011396
URL
[Cited within: 2]

We present a comprehensive study of velocity interpolation methods in polygons. These methods are often used as postprocessing procedures for numerical schemes that do not directly calculate the velocity field but only provide cell boundary flux conditions, such as the finite volume schemes. These methods extend the widely used velocity interpolation algorithms, such as the Pollock's algorithm, to more complex geometries such as perpendicular bisection (PEBI) grids, unstructured triangular grids and grids with local refinement. Once the velocity field is interpolated, streamline trajectories and time of flight along the streamlines can be calculated for reservoir simulation, model calibration and waterflood management, for instance. These velocity interpolation methods assume known lower-order or higher-order cell boundary fluxes, which satisfy global mass conservation and normal flux continuity. However, they differ in the interpolation of velocities within the interior of the cells. The interpolating velocity may be locally conservative or nonconservative, continuous or discontinuous, lower order or higher order. Results show that the interpolated velocity field has to be locally conservative in order to guarantee the correct volumetric transformation for the calculated streamlines and the time of flight. Velocity continuity is not as important as local conservation for the purpose of streamline applications. Compared to higher-order interpolation for the streamline trajectories, lower-order interpolation has the advantage of an analytic solution and an efficient implementation. Based on our analysis, we recommend a lower-order locally conservative method for the most robust and numerically efficient calculation of streamline trajectories on unstructured grids.
Semianalytical production simulation of complex hydraulic-fracture networks
Rules for flight paths and time of flight for flows in porous media with heterogeneous permeability and porosity