Introduction
The advancement of hydraulic fracturing and horizontal well technologies successfully unlock shale gas plays and yield commercial gas production[1,2]. The mechanical properties such as Young’s modulus, hardness, fracture toughness are critical for understanding hydraulic fracturing design and mechanisms of complex fracture network creation, while are also meaningful for sweet spot evaluation and wellbore drilling design. Conventional mechanical testing experiments including the uni-axial and tri-axial mechanical experiments, all have high demand on the core size and rock quality. However, because of chemical and physical instability of shales, it’s hard to acquire desirable standard cores, especially for full size cores with weak planes and natural fractures. All of these can bring with many difficulties in traditional mechanical testing. Besides, the expensive cost and long experimental time of conventional mechanical testing limit traditional mechanical experiments that are only available on local zones or key layers in exploration wells, which possibly resulting in discrete data and controversial conclusions. More importantly, it is hard to provide continuous mechanical profile for hydraulic fracturing design. Besides, the traditional mechanical experiments are destructive, after being loaded, the core is damaged and can’t be used for other tests and mechanical testing process on identical core is not repeatable[3,4]. Therefore, a simple and reliable mechanical testing approach is highly desirable in oil and gas industry.
Nanoindentation is one of the rapidly developing techniques for surface mechanical testing in recent years. Non-destructive, high resolution, and easy to do, it can be used to get key mechanical parameters such as hardness, Young’s modulus, plastic strain and fatigue strength of different materials. The application of nanoindentation technique has been used in rock mechanical testing and is gaining more and more attentions from researchers[5]. As it has much lower requirements on the size and quality of the tested sample, it can be done on cuttings, or side cores of pay zones or key formations of interest, which opens a new way for relating with and correction of well logs. The micro-structure, mineralogy, kerogen distribution of shale at nano scale are important for gas accumulation and rock deformation at macro scale. The combination of nanoindentation and some digital imaging techniques such as AFM (Atomic Force Microscope), digital core and 3D printing can relate mechanical properties at micro-scale with hydrocarbon migration, pore structure characterization. Chen et al.[6,7] used micron-scale mechanical test to analyze the hardness and elastic modulus of shale, and proposed a calculation model of rock mechanical parameters at micrometer scale. He also found that there was a good correlation between results from nanoindentation and microindentation. Bobko et al.[8] found that mineral particles of shale at the nano scale were transversely isotropic in stiffness and isotropy in strength. Shukla and Kumar et al.[9,10] tested and analyzed the mechanical properties of kerogen with nanoindentation technology and backscattered electron diffraction (BSE) (to calibrate the indentation position), and they found the elastic modulus of kerogen ranged from 5 to 9 GPa. Moreover, the higher content of kerogen would reduce the elastic modulus of rock. Liu et al.[11] used field emission scanning electron microscopy (FE-SEM) and digital image processing methods to establish the correlations between pore structure, pore size distribution and rock mechanics properties of Bakken shale at nano scale. Previous researches concentrated on testing of shale elastic modulus, hardness, and fracture toughness etc, and calculation of mechanical parameters with mean value statistic method, but few covered the distribution features of the mechanical parameters and model for upscaling nano-scale to micro-scale mechanical parameters. Moreover, few studies considered mechanical properties of shale with different bedding directions at nano scale, so it limits its wide application in characterizing mechanical properties of anisotropic shales[12,13,14].
In this work, the mechanical properties including elastic modulus, hardness and fracture toughness of shale collected from Silurian Longmaxi at Youyang area, Southwest of Chongqing, China were tested by grid nanoindentation approach. Rock samples with parallel and vertical bedding were taken from full size cores. The surface of rock samples were polished by sand paper and argon ion machine. With energy dispersive X-Ray fluorescence spectrometry (EDS), critical mechanical properties of marked minerals were tested and analyzed. In addition, the Weibull model was applied to investigate the distribution features of mechanical parameters and the reasons of discrete data. The Mori-Tanaka model was proposed to upscale the mechanical parameters from nano scale to macro scale, and the experimental results from uniaxial compression experiment were compared with those from indentation experiment to verify the accuracy of the latter. The study is of great benefit for studying the mechanical properties of Silurian Longmaxi shale at nano-scale and upscaling mechanical data from nano-scale to macro-scale.
1. Nanoindentation principle and experiment
1.1. Nanoindentation
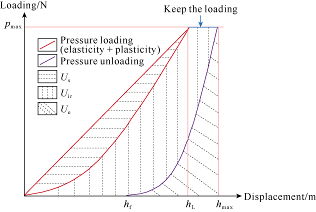
There is a stage of elastic deformation when the nanoindenter starts to press in rock surface. After that, the increasing load results in plastic deformation and an eternal indent can be observed according to geometry of indenters. When the unloading stage begins, the pure elastic deformation can be recovered and plastic deformation can create fracture. The load vs. displacement curve can be used to calculate the hardness and Young’s modulus of the rock (Fig. 1).
Fig. 1.
Fig. 1.
Nano-indentation load-displacement curve diagram (revised according to reference [12]).
The hardness can be calculated by Eq. (1)[15]:
The projected area Ac is the function of the contact depth hc:
There’s a relationship between hc and hmax:
Thus, the reduced modulus Er can be calculated by Eq. (5) with contact area and depth given:
The reduced modulus reflects the composite deformation of indenter and rock, the rock Young’s modulus E can be expressed as Eq. (6):
Rock fracture toughness represents the potential intrinsic ability of rock to withstand a given stress field at the tip of a crack and to resist against progressive crack extension[16]. The energy analysis and indentation shape methods can be used to calculate rock fracture toughness by nano-indentation experiment data. In this study, the former was used. Yang et al.[17] proposed that the fracturing energy can be calculated by the relations between pure plasticity Upp and irreversible energy Uir and expressed as Eq. (6):
The relation between pure plasticity Upp and total energy Ut can be written as Eq. (7):
The total energy Ut can be computed by:
To calculate the fracture toughness, the critical energy release rate Gc needs to be worked out first by Eq. (10) below:
The maximum contact area Am can be calculated by:
The fracture toughness can be computed by the Eq. (12):
1.2. Samples preparation
Four shale samples were drilled from full size cores at depth of 2 010 m of Silurian Longmaxi shale at Youyang area, Southwest of Chongqing, China. The cylinder samples parallel and vertical to the bedding plane were cut (25 mm in dimeter and 55 mm-60 mm long). Then, they were cut into standard cylinder samples (25 mm in dimeter and 50 mm long) for conventional uni-axial compressive test labelled as VA, VB, HA and HB, and samples for nanoindentation (25 mm in dimeter and 10 mm long) labelled as V1, V2, H1 and H2.
As local pores and bond interfaces between different minerals can potentially affect the accuracy of nanoindentation experiments, the surface of samples were carefully polished by SiC sand paper of different grit sizes from 600 to 1 200 first, and then by argon ion machine. Moreover, the digital Zeta-20 machine was used to scan the roughness of surface randomly to assure the roughness met the requirement for nanoindentation test. Then the samples were ultrasonic cleaned and treated with acetone to remove dust[18,19]. The RoqSCAN equipment was used for mineral composition analysis, and Scanning Electron Microscopy (SEM), Back scattered Electron Imaging (BSE) and Energy Dispersive Spectroscopy (EDS) can be obtained simultaneously to map the mineral distribution of each indents. Additionally, SEM was secondly performed on the rock surface after nanoindentation to get the indentation fracture morphology.
The nanoindentation experiments were performed on a Nanoindenter (Agilent Technologies G200) with load resolution of 50 nN, standard peak load of 500 mN, displacement resolution of less than 0.01 nm in the z direction and 1 μm in the x and y direction. Moreover, the least indentation depth for each nanoindentation experiment was greater than 500 μm, with a travel range of 100 mm×100 mm. The tip radius of curvature for Berkovich diamond was less than 20 nm.
1.3. Experimental process
The experiment was divided into three steps.
(1) The indenter approached the sample surface at the loading rate of 30 nm/s, sudden increase of load shown by the testing system meant the indenter contacted the sample surface already, then the load and indentation depth were recorded automatically. The maximum load of each indentation was set at 500 mN. The force was held constant at the maximum indentation for 15 seconds.
(2) Prior to the nanoindentation test, the tip area function was calibrated by several indentations on a standard fused quartz sample. The nanoindentation tests were performed on a 4 by 8 grid at 15 μm spacing between indentations (The total individual indentations were 128 for all four samples). By this test method, a group of hardness, Young’s modulus and fracture toughness were obtained for each indentation to calculate the average mechanical parameters of each sample. EDS was used to analyze the sample surface and position special minerals, then the mechanical properties of special minerals were calculated.
(3) The compression tests on the samples were performed on a triaxial testing apparatus that could independently apply confining stress and axial stress. The macroscale results of uniaxial compression tests were compared with that obtained by nanoindentation.
2. Results
2.1. Mineral composition and microstructure of shale
BSE scanning results of shale samples from Longmaxi Formation show that the samples have good cementation of particles, few large pores and only a small number of small pores (Fig. 2a). The quality fraction and area fraction of mineral composition and mineral analysis statistics were obtained by EDS mapping data (Table 1). The results show that the rock is mainly composed of quartz minerals (quartz, feldspar, potassium feldspar), carbonate minerals (calcite, dolomite), clay minerals (illite, kaolinite, chlorite), but also contains a small amount of saponite, dolomite, pyrite and amorphous substances difficult to distinguish.
Fig. 2.
Fig. 2.
Analysis and test results of vertical bedding components of shale mineral.
Table 1 Analysis results of shale composition.
| Parameter | Mass fraction/% | Area fraction/% | |
|---|---|---|---|
| Quartz class | Quartz | 27.38 | 26.92 |
| Albite | 21.52 | 23.94 | |
| Potash feldspar | 1.91 | 2.20 | |
| Carbonate | Calcite | 4.47 | 5.12 |
| Bitter spar | 1.64 | 2.12 | |
| Clay class | Illite | 24.77 | 20.15 |
| Kaolinite | 2.13 | 1.22 | |
| Chlorite | 2.10 | 1.77 | |
| Else | 9.88 | 12.86 | |
SEM results of gird matrix indentations and single nano indentation (Fig. 3a, 3b) show that there are some intrinsic pores and micro cracks in the samples. Thus, in the nanoindentation process, the increase of load with the rise of displacement would generate fractures. The propagation of fractures would be affected by the micro-defects of the sample, and would likely to go along the edges of existent pores or microcracks. Due to the heterogeneity of the sample, if the indentation location is just on hard materials like carbonate, and below it is soft material like clay, the so-called “base effect” (clay gathering) could occur, which can affect the nanoindentation results.
Fig. 3.
Fig. 3.
Grid matrix indentations SEM image (a) and single indentation SEM image (b) after nano indentation.
2.2. Load-displacement curve
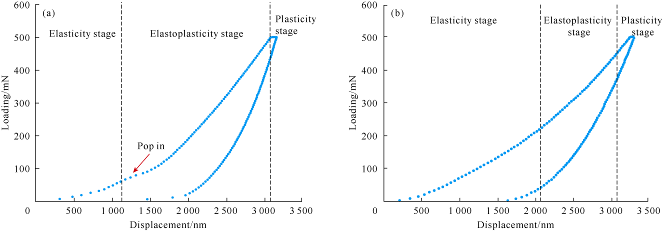
The Load-displacement curve is base to analyze deformation behavior and mechanical parameters of nanoindentation. The load-displacement curves obtained are not smooth in certain stages, and there are some “pop in” behaviors at the loading stage (Fig. 4a). The main reason for “pop in” is that when the load approaches to the yield strength of rock, fractures occur. As the fracture tip begins to expand inward rock, and the process continues until load stops. In addition, the heterogeneity of the shale also could cause “pop in” behavior, especially indentation fractures contact with internal defects such as micro-cracks, pores, or interface between hard material and soft materials such as kerogen.
Fig. 4.
Fig. 4.
Load - displacement curves with “pop in” (a) and normal (b) nano indentation.
There are three stages in the loading process during nanoindentation experiment: elastic deformation, elastoplastic deformation and plastic deformation. The differences in rock mechanical properties result in different durations of the stages. Fig. 4a shows that the sample enters the elastoplastic phase from elastic phase at the displacement of 1 000 nm, while Fig. 4b shows that the sample enters elastoplastic phase from elastic phase after the displacement of 2 000 nm. During the loading process, the curvature of the load-displacement curve will increase rapidly in the elastic and elastoplastic stages, which reflects the rapid elastic deformation when nano-indenter contacts shale surface. When the load reaches the yield strength of the rock, elastoplasticity occurs. When the indentation load exceeds the strength of the rock, permanent deformation would cause nanoindentation fractures.
2.3. Test results of mechanical parameters on nano scale
According to the load-displacement curve, the mechanical parameters such as hardness and elastic modulus of rock can be calculated by using equations (1) and (6) respectively, and the fracture toughness of rock can be calculated by equation (12). Due to the large amount of data in nanoindentation experiment, the averaging method or the deconvolution method is usually used to process the mechanical parameters. The deconvolution method needs to distinguish the rock components clearly and may have multiple solutions. Therefore, the averaging method was adopted for data analysis in this work. Statistics on 128 groups of mechanical parameters show (Table 2) the samples with parallel bedding planes have an average elastic modulus of 45.21 GPa (standard deviation of 5.59 GPa), average hardness of 2.43 GPa (standard deviation of 0.56 GPa), and average fracture toughness of 2.68 MPa•m1/2 (standard deviation of 0.33 MPa•m1/2). The samples with vertical bedding planes have an average elastic modulus of 43.60 GPa (standard deviation of 4.03 GPa), average hardness of 2.85 GPa (standard deviation of 0.78 GPa), and average fracture toughness of 2.37 MPa•m1/2 (the standard deviation of 0.66 MPa•m1/2). The samples with parallel bedding planes have slightly higher elastic modulus and fracture toughness than those with vertical bedding planes. At nano scale, as the indentation points are on different minerals, the mechanical parameters tested would fluctuate somewhat. Therefore, in order to obtain representative and reliable mechanical parameters, more indentation points need to be tested to mitigate the uncertainty caused by rock heterogeneity.
Table 2 Mechanical parameters by average method from nanoindentation test.
| Coring angle | Elastic modulus/GPa | Hardness/GPa | Fracture toughness/(MPa·m1/2) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Average | Standard deviation | Minimum | Maximum | Average | Standard deviation | Minimum | Maximum | Average | Standard deviation | |||
| Parallel bedding | 35.61 | 59.47 | 45.21 | 5.59 | 1.58 | 3.89 | 2.43 | 0.56 | 2.02 | 3.41 | 2.68 | 0.33 | ||
| Vertical bedding | 37.41 | 53.80 | 43.60 | 4.03 | 1.79 | 4.58 | 2.85 | 0.78 | 0 | 2.94 | 2.37 | 0.66 | ||
With the help of EDS mineral calibration results, the mechanical parameters of specific minerals can be obtained after the nanoindentation test, which provides parameters for the upscaling model. The mechanical test results of specific minerals obtained in this study are in good agreement with the experimental results of other researchers[9,10] (Table 3). Due to the low content of minerals such as chlorite and pyrite in the samples, no relevant indentation data was recorded. In addition to nanoindentation on specified minerals, nanoindentation was also conducted on the interface between quartz and clay minerals. The results show that dolomite and quartz have the highest elastic modulus of 115 GPa and 99 GPa, respectively; the elastic modulus of clay is the lowest, that of kaolinite and illite are 55 GPa and 62 GPa, respectively; and that of the mixed mineral of quartz/clay matrix is about 59 GPa.
Table 3 Mechanical parameters of specific minerals from nanoindentation.
| Mineral classification | Mineral | Elasticity modulus/GPa | |
|---|---|---|---|
| Mean value of this paper | Data in literature [9-10] | ||
| Clay class | Kaolinite | 55 | 56 |
| Illite | 62 | 66 | |
| Carbonate | Calcite | 79 | 85 |
| Dolomite | 115 | 125 | |
| Quartz class | Quartz | 99 | 100 |
| Albite | 72 | 68 | |
| Else | Pyrite | / | 250-310 |
| Quartz/clay matrix interface | 59 | / | |
3. Discussion
3.1. Correlation between different mechanical parameters at nano scale
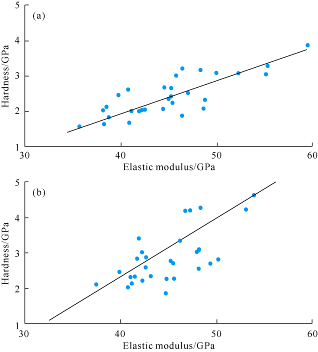
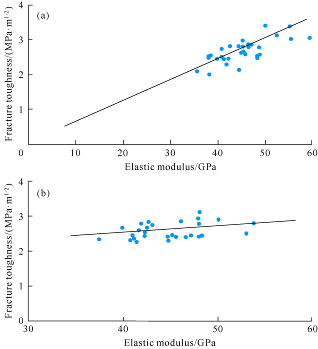
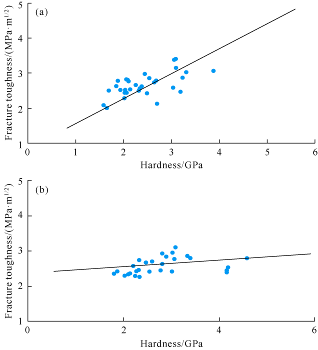
From linear regression, there is a positive correlation between Young’s modulus and hardness of shale samples with parallel and vertical beddings. The correlation coefficients are 0.57 and 0.58 for rock samples with parallel and vertical beddings, respectively (Fig. 5). There is also a positive correlation between Young’s modulus and fracture toughness of shale samples with parallel and vertical beddings. The correlation coefficients are 0.54 and 0.51 for them respectively (Fig. 6). However, there is poor linear relationship between hardness and fracture toughness with correlation coefficients of 0.31 and 0.36 (Fig. 7). That’s because the calculation of hardness depends on the contact projection area and load, but the fracture toughness calculation uses the sum of the shaded areas as input. The differences in the inputs for computation result in discrepancy. Therefore, to reduce the discrepancy, the contact depth, contact stiffness and residual depth must be calculated more accurately besides increasing indentation points tested.
Fig. 5.
Fig. 5.
The relationship between elastic modulus and hardness of samples with parallel bedding (a) and vertical bedding (b).
Fig. 6.
Fig. 6.
The relationship between elastic modulus and fracture toughness of samples with parallel bedding (a) and vertical bedding (b).
Fig. 7.
Fig. 7.
The relationship between hardness and fracture toughness of samples with parallel bedding (a) and vertical bedding (b).
3.2. Distribution of different mechanical parameters at nano scale
Nanoindentation results show that there are some fluctuation in Young’s modulus, hardness and fracture toughness of the same sample. Take Young’s modulus of rock samples with parallel beddings for instance, the maximum value is 59.47 GPa, while the minimum value is 35.61 GPa. The maximum value is 1.67 times of the minimum value. The reason is the heterogeneity of the samples. Therefore, the test results of nanoindentation need to be analyzed statistically to find their uncertainty. Previous studies on rock mechanical parameters distribution show Weibull model can effectively characterize heterogeneity and mechanical response features of rock under external force. More importantly, the parameters in this model can be easily measured[20,21]. The Weibull model can be expressed as:
where Pw is the probability that the mechanical parameter value is less than X, Xi is the characteristic mechanical parameter. X0 is generally set at 0, representing the minimum variable value. The reliability parameter m named Weibull modulus, reflects the scatter of mechanical parameters. The higher the m, the lower the discreteness of the parameter will be.
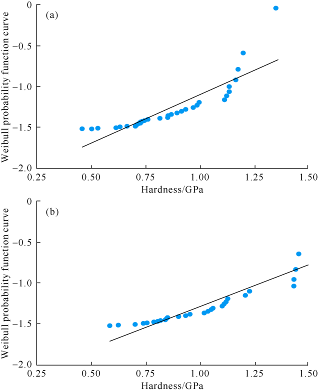
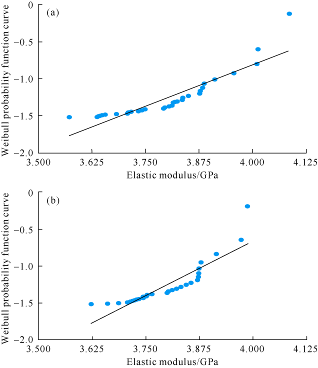
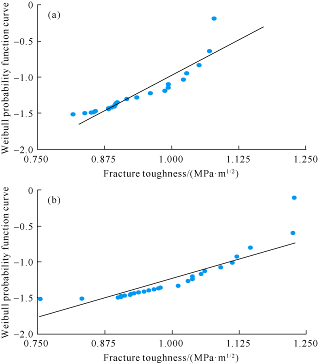
The statistical results obtained from nanoindentation experiments were arranged in numerical order to get the probability of each experiment result no more than X (Table 4). The m value was worked out by least square method (LSM) (Figs. 8-10). The m of three mechanical parameters are all small, indicating the test results of nanoindentation are high in discreteness, among them, the m of hardness is the smallest, indicating hardness has the highest discreteness. The root causes of the data discreteness are: Firstly, the different size, shape and arrangement of mineral particles on the surface and in the interior of rocks, and different positions of indentation lead to differences in experimental results. Secondly, when the fracture from indentation propagate, mineral particles with large size or strong strength could change the local stress field distribution, leading to deviation and blockage of indentation fracture, and thus jump in experimental data. Thirdly, the calculation of hardness only considers the indentation shaded area, but the arrangement of hard and soft substances in rock interior can possibly create “base” effect, affecting the accuracy of calculated projection shaded area, and consequently the precision of hardness calculated. Moreover, the m value of samples with vertical beddings are all lower than that of samples with parallel beddings, which indicates that the samples with vertical beddings have higher heterogeneity than those with parallel beddings.
Table 4 Statistics on m values of nano indentation mechanical parameters.
| Coring angle | m value of fracture toughness | m of the elastic modulus | m of hardness |
|---|---|---|---|
| Parallel bedding | 3.73 | 2.99 | 1.18 |
| Vertical bedding | 2.12 | 2.27 | 1.01 |
Fig. 8.
Fig. 8.
Hardness Weibull curve of samples with parallel bedding (a) and vertical bedding (b).
Fig. 9.
Fig. 9.
Weibull curve of elastic modulus of shale samples with parallel bedding (a) and vertical bedding (b).
Fig. 10.
Fig. 10.
Weibull fracture toughness curve of shale samples with parallel bedding (a) and vertical bedding (b).
3.3. Upscaling model of mechanical parameters from nano scale to micro scale
During the nanoindentation test, it’s easy to indent on different materials without the aid of EDS mapping, thus resulting in discrete test results. To get more accurate bulk mechanical parameters of rock, it’s necessary to increase the number of indents in the same rock surface. By comparing the nanoindentation results of different minerals, the mechanical parameters of different minerals in the same sample differ widely. But the whole rock can be regarded as a composite media composed of three-phases, the high strength minerals (dolomite, et al.), medium strength minerals (quartz, albite, calcite, et al.) and low strength minerals (clay, organic matter, etc.). Moreover, the three types of minerals can be regarded as isotropic at the nano scale. By joining the volume fraction of different phases and the composition mechanical model, the mechanical properties of bulk rock by upscaling from nano- scale to centimeter scale can be obtained. It should be noted that there are possible nano and micro pores in clay or kerogen, thus the calculation of mechanical properties of bulk rock should consider natural fracture, nano and micro pores.
where r=0 represents carbonate minerals such as dolomite et al., r=1 denotes quartz minerals such as quartz and albite et al., r=2 represents clay minerals.
The minerals with the highest strength and medium strength can be obtained directly by combining nanoindentation data and EDS mapping. However, the low strength minerals should consider porosity of rock (The porosity of rock assumed as 3.5% in this study), since nano and micro pores would affect the results of nanoindentation test. The shear and bulk modulus of low strength mineral can be computed by:
The Young’s modulus of bulk rock can be obtained by three-phase minerals and relating volume fractions:
Fig. 11.
Fig. 11.
The petrophysical model (a) converted to equivalent mechanical parameter model (b).
To further demonstrate the accuracy of the upscaling model, uniaxial compression tests were performed on cylinder shale samples to get stress vs. strain curve and calculate the Young’s modulus (Fig. 12).
Fig. 12.
Fig. 12.
Shale uniaxial compression stress-strain curve.
Table 5 shows mechanical parameters obtained from three different methods. We can see that the calculated values from the upscale model have a good agreement with those obtained by uniaxial compression tests, but the calculated results by the averaging approach of nanoindentation data are higher in values. The mechanical properties are different at different scale and this is because test samples at larger size have more natural micro pores and fractures, thus the increase of load can induce fracture extension from natural damage area and grow as interconnected fractures. Although the upscale model provides a good tool to characterize bulk mechanical properties and potentially reduce the number of nanoindentation, the combination of the nanoindentation and mineral mapping technique at the rock surface is necessary to get reliable mechanical properties of each phase.
Table 5 Upscaling elastic modulus results.
| Coring angle | Young’s Modulus by compression test/GPa | Young’s Modulus by upscaling model/GPa | Young’s Modulus by averaging approach/GPa |
|---|---|---|---|
| Parallel beddings | 41.12 | 45.21 | 48.52 |
| Vertical beddings | 39.15 | 43.60 | 45.25 |
4. Conclusions
A total of 128 nanoindentation experiments were carried out on Longmaxi shale samples with parallel and vertical beddings. The hardness, Young’s modulus and fracture toughness of the shale samples were obtained by load-displacement curve. Additionally, mechanical parameters of samples with parallel bedding are slightly higher than those of samples with vertical bedding. There is a good linear correlation between Young’s modulus and hardness, and between Young’s modulus and fracture toughness.
The results of mechanical parameters at nano scale show certain discreteness and conform to Weibull distribution. The hardness data has the highest discreteness. The discreteness of mechanical parameters not only is related to the heterogeneity of shale, but also is affected by occasional and regional fracture propagation resistance due to non-uniform mineral distribution. Besides, taking shaded area below displacement vs. load curve only as parameter in calculation is another reason of the discreteness.
The combination of BSE and EDS mapping was used to analyze the mechanical properties of certain minerals in nanoindentation measurements. A micro-mechanical model consisting of three-phase media (high-strength minerals, medium-strength minerals and low-strength minerals) was proposed. The Mori-Tanaka model was used to upscale data from nano scale to micro scale, and the results were compared with results from averaging method and uniaxial compression test, which shows the calculated values from the upscale model are in good agreement with the results from uniaxial compression test, but lower than those from nano-scale calculation. This is because the samples have natural micro pores and fractures etc, leading to differences in their mechanical properties.
Acknowledgements
Special thanks to Professor YANG Jijin and Professor DU Zhongming from Institute of Geology and Geophysics at Chinese Academy of Sciences for their help with the experiments.
Nomenclature
Ac—the area of contact projection under the corresponding load, m2;
Amax—maximum contact projection area under corresponding load, m2;
E—Young’s modulus of the sample, Pa;
EHOM—equivalent elastic modulus of the rock at centimeter scale, Pa;
Ei—elastic modulus of Berkovich indenter, 1 114 GPa;
Er—elastic modulus of different minerals, Pa;
Er—reduced Young’s modulus, Pa;
fr—volume fraction of different minerals, %;
Gc—critical energy release rate, N/m;
GM—bulk modulus, Pa;
hc—contact depth, m;
hf——residual depth, m;
hL—initial displacement of the holding point, m;
hmax—maximum displacement, m;
H—hardness, Pa;
Klow—equivalent volume modulus for low strength minerals, Pa;
Kc—fracture toughness, Pa·m1/2;
KM—shear modulus, Pa;
ks—the proportion of clay minerals, %;
kr—volume modulus of different mineral particles, Pa;
m—Weibull modulus, dimensionless;
pc—load, N;
pmax—maximum load, N;
Pw—probability of lower than the random variable;
S—contact stiffness, N/m;
Uc—fracture energy, N·m;
Ue—elastic energy, N·m;
Uir—irreversible energy, N·m;
Upp—energy lost during pure plastic stage, N·m;
Us—nanoindentation absolute energy, N·m;
Ut—total fracture energy, N·m;
X—random variable;
X0—the minimum parameter value of the random variable;
Xi—characteristic parameters;
β—a constant related to the geometry of indenter;
ϕ—shale porosity, %;
μlow—equivalent shear modulus for low-strength minerals, Pa;
μs—shear modulus of clay minerals, Pa;
μr—shear modulus of different minerals, Pa;
ν—Poisson’s ratio of sample, dimensionless;
νE—elastic energy ratio, dimensionless;
νi—Poisson’s ratio of Berkovich indenter, 0.77;
νr—Poisson’s ratio of different minerals, dimensionless;
ε—constant, 0.75.
Reference
Hydraulic fracture propagation geometry and acoustic emission interpretation: A case study of Silurian Longmaxi Formation shale in Sichuan Basin, SW China
Petrophysical properties characterization of Ordovician Utica shale in Quebec, Canada
DOI:10.1016/S1876-3804(16)30008-8
URL
[Cited within: 1]

With multiple techniques, the following measurements and analysis were made to characterize the Ordovician Utica shale samples: mineralogy, porosity, microstructure, and surface wettability etc. The test of mercury injection apparatus showed that the pore size of Utica shale is 15 200 nm. X-ray diffraction (XRD) mineralogy analysis and Energy-Dispersive X-ray Spectroscopy (EDS) indicated that in Utica shale non-clay minerals are dominated by calcite and quartz, while clay minerals by illite and chlorite. With the images from scanning electron microscope (SEM), the surface microstructure examination showed various types of pores exist in Utica shale, such as intragranular, intergranular, organic etc. And the pores in organic matter (kerogen) were found in nanometer size (10 to 50 nm). A three-dimensional tomography model and a geometry model of the pores space using FIB-SEM imaging tomography were reconstructed with 250 SEM images. It provides visual insights into the petrophysical properties of Utica shale. Finally, the wettability tests displayed that Utica shale has weak-water wet to intermediate wettability.
A new multi- functional true triaxial fluid-solid coupling experiment system and its applications
DOI:10.13722/j.cnki.jrme.2015.0050
URL
[Cited within: 1]

A new multi-functional true triaxial fluid-solid coupling experiment system was designed,fabricated,calibrated,and successfully tested to better simulate in-situ triaxial stress conditions and reveal geomechanical properties and seepage laws for rocks and coals subjected to these conditions. The experiment system comprises a load frame,a true triaxial pressure vessel,a high pressure loading system,an internally sealed seepage system,a control and data acquisition system and an acoustic emission monitoring system. The advantages and innovations of the experiment system include:(1) Geomechanical and seepage experiments can be performed for different stress-strain paths under uniaxial,biaxial or true triaxial stress conditions.(2) Three new stress and strain control modes(Trace-F,Trace-D and Trace-Df) are implemented to ensure that the center point of the specimen stays in the same position during experiments.(3) The internally sealed seepage system is designed to accomplish the independent control and monitoring of fluid flow in the specimen under true triaxial stress conditions.(4) To reduce the specimen end friction effect,stiff loading mode is applied in two directions and either flexible or stiff loading mode is applied in the third direction. In addition,high frequency dynamic control is implemented for the load system,therefore experiments with complex stress-strain paths can be performed.(5) New multi-functional loading platens are designed to accommodate hydraulic fracturing experiments.(6) The experiment system can apply a force of up to 6 000 k N in each of two directions and 4 000 k N in the remaining direction. The applied fluid pressure can be up to 60 MPa based on a servo-controlled supercharger. A series of testing methods and experiments were performed to verify the accuracy and reliability of the experiment system. This system will provide a comprehensive new tool to study geomechanical properties and seepage laws for rock and coal under true triaxial stress conditions,which can be further applied to research in areas such as geological storage of CO2,efficient oil-gas exploitation and deep underground rock engineering applications.
Experimental study of microstructure and rock properties of shale samples
The mechanical properties of shale based on micro-indentation test
DOI:10.1016/S1876-3804(15)30069-0
URL
[Cited within: 1]

In view of the difficulty to get mechanical characteristics of shale reservoirs, a quantitative evaluation method based on micro-indentation test technology was proposed to research the meso-mechanical properties of shale. Through micro-indentation test of shale outcrop samples from the Cambrian Longmaxi Formation in the Changning area, Sichuan Basin, the meso-mechanical properties of shale were analyzed, and the relationship between the macro-scale and meso-scale shale mechanical properties was evaluated. The analysis results of micro-indentation tests show that the mesoscopic elastic modulus and indentation hardness are heterogeneous in distribution. The comparison of macro and meso experiments shows that the statistical mean value of meso-elastic modulus is approximate to the value of the macro-elastic modulus. The relationship between composition and mechanical properties of shale was obtained based on the packing density model theory. The result shows that mesoscopic elastic modulus and indentation hardness increase nonlinearly with the increase of the packing density. Based on the hardness-packing density model, the reverse analysis of cohesion and friction angles shows that the mesoscopic value is slightly smaller than the macroscopic value. The micro-indentation test technology can evaluate shale meso-mechanical properties and predict the macro-mechanical properties effectively.
A comparative experiment investigate of strength parameters for Longmaxi shale at the macro- and mesoscales
DOI:10.1016/j.ijhydene.2017.05.240
URL
[Cited within: 1]

The strength parameters of rock is important to the storage and development of hydrogen gas and natural gas. The rock strength parameters is the basis of the establishment of storage space and wellbore, especially for the shale formation. However, the strength parameters and indentation mechanism of shale are unclear. It is necessary to research the strength parameters and dynamic indentation of shale from the multiscale perspective. A comparative experimental study of shale indentation at the macro- and mesoscales was conducted. The experimental investigate determined the four stages of shale indentation at the mesoscale. With increasing loading rate at the same load value, indentation depth decreases, and the critical fracture load of shale increases. The result shows that the indentation load can improve the rate of penetration, but the shale strength increases slightly at the same time, which suppresses the energy release of the shale fragmentation. The probability of indentation fragmentation occurs 2 3 times at the mesoscales is greater than 4 times the value at the macroscale. The macro averages of shale hardness and elastic modulus are close to the mesoscale values. The differences are 7% and 5.5%, respectively. The study results can be used in the storage and development of hydrogen gas and the optimization design of drilling tools.
The nano-mechanical morphology of shale
DOI:10.1016/j.mechmat.2007.09.006
URL
[Cited within: 1]

Shale, the sealing formations in most hydrocarbon reservoirs, is made of highly compacted clay particles of sub-micrometer size, nanometric porosity and different mineralogy. In this paper, we propose and validate a technique to identify the nano-mechanical morphology of such a nanocomposite material. In particular, by means of a massive nanoindentation campaign at two different scales on a large range of shale materials, we show that the highly compacted plate- or sheet-like clay particles have a distinct nano-mechanical morphology with no privileged orientation of the particle-to-particle contact surface, as evidenced by a mechanical percolation threshold of 0 0.5. Furthermore, the nanoindentation results provide strong evidence that the nano-mechanical elementary building block of shales is transversely isotropic in stiffness, and isotropic and frictionless in strength. These observations lead to a sphere-like mechanical morphology for visibly plate- or sheet-like clay particles. The contact forces between the sphere-like particles activate the intrinsicly anisotropic elastic properties within the clay particles and the cohesive bonds between the clay particles. The mechanical stiffness and strength properties of porous clay scale with the clay packing density toward a unique set of shale-invariant material properties. The determination of mechanical microstructure and invariant material properties are of great importance for the development of predictive microporomechanical models of the stiffness and strength properties of shale. The approach presented here also applies to other chemically and mechanically complex materials exhibiting nanogranular behavior.
Estimation of elastic properties of organic matter in Woodford shale through nanoindentation measurements
DOI:10.2118/162778-MS
URL
[Cited within: 2]

Shales are one of the most heterogeneous and complex natural materials found. Recent spike in the activities in shale gas and oil plays has been possible through horizontal drilling and hydraulic fracturing, which requires better understanding ofmechanical properties. Complexities associated with elastic properties of shale are amplified with presence of wide range of organic fraction present in them. There is a need to understand the mechanical properties of organics and their associatedimpact on bulk mechanical properties.
Microstructural and geomechanical analysis of Bakken shale at nanoscale
DOI:10.1016/j.petrol.2017.03.039
URL
[Cited within: 1]

With the development in production from shale oil and shale gas in North America during the last decade, more studies are being conducted in order to improve our knowledge of the shale characteristics. In this paper, samples from Upper and Middle Bakken Formation, which is an oil-bearing shale formation, were collected and analyzed. Permeability, porosity and saturation of the samples were studied in the lab. 2D XRD and EDX were used to study the mineral compositions, and FESEM was used to characterize the pore structure at micro and nanoscale. Implementing the image analysis method, the pore structure and pore size distributions (PSD) of the samples at nanoscale were quantified. In addition, nanoindentation method, which is a novel technique to investigate the geomechanical behavior of rocks, was applied to quantify the mechanical properties of the shale samples including Young's modulus, hardness, and fracture toughness at nanoscale.
Macroscale Young’s Moduli of shale based on nanoindentations
Applications of nano-indentation methods to estimate nanoscale mechanical properties of shale reservoir rocks
DOI:10.1016/j.jngse.2016.09.068
URL
[Cited within: 1]

61Nano-indentation method was used to analyze the mechanical properties of shale from Bakken Formation.61Abnormal phenomena from the nano-indentation curves were reported and their causes were explained.61Elastic modulus and Hardness values of samples at nanoscale were calculated and their relationships with mineral compositions and microstructures were investigated.61Energy analysis method was used to quantify the nanoscale rock fracture toughness.
An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments
DOI:10.1557/JMR.1992.1564 URL [Cited within: 1]
Measurement and interpretation of shale toughness under confining pressures
Based on the fracture mechanics theory under confining pressure conditions, the authors test rock fracture toughness using the thick-wall cylinder specimens with double-wing fractures and different clay contents under various confining pressures. The authors then use the finite element model to interpret the toughness results. The regression analysis based on a number of experiments indicates that the relationships of fracture toughness with confining pressure and shale contents are linear with small errors. The experimental procedures and interpreting method presented in this paper assure a better accuracy for determination of fracture toughness for hydraulic fracturing than that obtained from experiments without confining pressures, and are thus favorable for improvement of hydraulic fracturing performance.
Scaling relationships for indentation measurements
DOI:10.1080/01418610208235693
URL
[Cited within: 1]

Using dimensional analysis and finite-element calculations, several relationships that relate features of indentation loading and unloading curves to the hardness, the elastic modulus and the work of indentation are extended to conical indentation in elastic-plastic solids with various angles. These relationships provide new insights into indentation measurements. They may also be useful to the interpretation of results obtained from instrumented indentation experiments.
Analysis of continuous stiffness data measured during nanoindentation of titanium films on glass substrate
DOI:10.1016/j.matchemphys.2010.10.026
URL
[Cited within: 1]

An empirical function was proposed to describe the continuous stiffness curves, i.e., versus h (where Er is the reduced modulus, H is the composite hardness and h is the indenter penetration depth), measured with nanoindentation tests for titanium films on glass substrate. By analyzing the variations of the parameters included in this empirical equation with film thickness, the physical meanings of this empirical equation were discussed. It was shown that the mechanical properties of the substrate and the film may be extracted from such analyses.
Research on influence of inhomogeneity degree on mechanical parameters of inhomogeneous rock
Modeling the effects of heterogeneity and anisotropy on the excavation damaged/disturbed zone (EDZ)
DOI:10.1007/s00603-009-0177-3
URL
[Cited within: 1]

When modeling the mechanical behavior of underground excavations, it is necessary to include the influence of the rock mass characteristics on the Excavation Damaged/Disturbed Zone (EDZ). In this paper, the Realistic Failure Process Analysis code, RFPA, is used to model the extent of the EDZ. The inhomogeneous characteristics of rock at the mesoscopic level are included by assuming that the material properties of the constituent elements conform to a Weibull distribution; the anisotropy is incorporated as a transversely isotropic medium; the non-elastic characteristic is simulated via an elastic damage-based constitutive law. A finite element program is adopted as the basic stress analysis tool. In this study, a notable feature is that no a priori assumptions need to be made about where and how fracture and failure will occur cracking can take place spontaneously and can exhibit a variety of mechanisms when certain local stress conditions are met. The deformation and failure process of anisotropic rock around excavations of different geometries is analyzed, and compared to experimental tests, showing similar fracture patterns. Additionally, the effect of confining stress and of different material layers is modeled and discussed. It is found that the model clearly illustrates that fracturing, both initiation and propagation, occurs as a combination of the stress concentrations and weakness planes introduced via the transverse anisotropy 鈥 which could represent either foliations or ubiquitous joint sets.
Average stress in matrix and average elastic energy of materials with misfitting inclusions
DOI:10.1016/0001-6160(73)90064-3
URL
[Cited within: 1]

Having noted an important role of image stress in work hardening of dispersion hardened materials, (1,3) the present paper discusses a method of calculating the average internal stress in the matrix of a material containing inclusions with transformation strain. It is shown that the average stress in the matrix is uniform throughout the material and independent of the position of the domain where the average treatment is carried out. It is also shown that the actual stress in the matrix is the average stress plus the locally fluctuating stress, the average of which vanishes in the matrix. Average elastic energy is also considered by taking into account the effects of the interaction among the inclusions and of the presence of the free boundary.
Study of equivalent elastic modulus of sand gravel soil with Eshelby tensor and Mori-Tanaka equivalent method
Sandy pebble soil is a granular media,and the physico-mechanical properties of sandy pebble soil are different from those of sandy soil and intact rock mass.Here sandy pebble soil is considered as a simplified material,namely a two-phase composite material consists of sandy soil as matrix and pebble as ellipsoid inclusion.This paper presents the theoretical derivation of equivalent elastic matrix calculation equation.The derivation process is based on Eshelby tensors and Mori-Tanaka equivalent method within small deformation condition.The process is also considered pebble content and distribution,using replacement iterative method.This paper focuses on the calculation of sandy pebble soil equivalent elastic modulus using numerical solution through compile program.Comparison is made between numerical solution and theoretical result.The result shows that the theoretical calculation method has better calculation accuracy than the earlier calculation methods of previous experiment and theory.When the pebble volume fraction less than 50%,the result of theoretical calculation coincides with experiment result,thus the presented method can be used to predict sandy pebble soil macroscopic mechanical properties,and it is beneficial to underground engineering application;when the volume fraction more than 50%,the theoretical calculation result may have some error with the experiment result.