Introduction
The term “quantitative assessment” in the title refers to the consistency check of the finally selected static model with actual data and geological understanding, and to the relative assessment of the model accuracy under current conditions of available data and cognitive capacity, including but not limited to quality control for a certain process of modeling.
New techniques of 3-D geological modeling have developed by leaps and bounds in recent years. By contrast, papers on discussing how to systematically evaluate the quality of 3-D geological models are considered rare, especially the quantitative evaluation of the finally screened geological model. Professionals seem to pay more attention to modeling methodology than model reliability. Overseas scholars are accustomed to quality control of 3-D models from the perspective of accuracy assurance or reducing uncertainties[1,2,3]. However, its primary purpose is not the quality evaluation of the final model. Chinese colleagues prefer discussing some major issues which may have a significant impact on the quality of final model, verifying the model with static and dynamic data[4,5,6,7,8,9], but it is still a qualitative evaluation as a whole. Although there are highly visible efforts in the field of quantitative evaluation[10], the single-parameter evaluation is not robust. There are two reasons for the lagging development of quantitative evaluation. Firstly, due to the complexity of subsurface geological settings in oil or gas fields and different data conditions, there is no comparability, and thus the universal framework for evaluating model quality is currently not available in the public domain[5]. Secondly, on account of different types of reservoirs and different development stages, it is difficult to select common evaluation parameters and establish uniform quantitative standards. However, fundamentally, it is the traditional way of thinking without differentiating reservoir types that restricts the establishment and development of the quantitative evaluation criteria of 3-D geological model. If we narrow the evaluation scope down to the same reservoir type, or even to the same research target, the comparability and practicability of the quantitative assessment will be emerging, such as the following two cases: the quantitative assessment can enable different geological models to be compared, which have been created by different researchers using the same data, so as to provide options for decision makers; it also facilitates the exchanges between inspectors and geo-modelers to grasp jointly key points of assessment and reach consensus. Compared to qualitative evaluation, the multi-parameter quantitative assessment not only has objective and comprehensive advantages, but also can identify the aspects to be improved according to the deducting points. In short, it is of great importance to establish and develop the quantitative assessment standard and to evaluate models in accordance with it. It is a necessary supplement to the workflow itself. In the future, the test of the reliability of geological models will become a research hotspot in the field of reservoir modeling and develop towards refinement and standardization[8].
Oil and gas reservoir description can be categorized into four types from the perspective of geological modeling: oil-reservoir description of large stable sedimentary system, oil-reservoir description of complex fault block, low permeability oil/gas-reservoir description and fractured oil-reservoir description[11]. Taking the oil reservoir in complex fault block as an example, we discuss the multi-parameter quantitative evaluation method of 3-D geological models.
1. Evaluation strategy
We started the research with a wide investigation of characteristic parameters which are most likely to impact the quality of oil-reservoir model for complex fault block, and then designed a survey form, involving evaluation system, methods, associated parameters and weights, to collect the feedback from ten experts with over 30 years of work experience and high popularity in the petroleum industry, including four geologists, two geophysicists, two petrophysicists and two reservoir engineers. The multi-parameter quantitative evaluation criteria were established based on the investigation and the consultation. The evaluation strategy includes four points as follows:
(1) The quantitative evaluation system is composed of three main parts, namely, data verification, geological understanding and process check. Data verification is to verify the accuracy of local prediction based on actual data in the field (hard data). Geological understanding is to examine whether the global estimation honors geologic rules and prior understanding (soft data). Both of them check the model quality from a view of direct information and indirect information respectively, and complement each other, which are the focus of quantitative assessment. Therefore, they are weighted by 60 points and 20 points respectively in centesimal system. To avoid occasionality, process check is indispensable, weighting 20 points.
(2) The evaluation adopts PCA (Principal Component Analysis) method[12], which has the ability to incorporate all experts' opinions on characteristic parameters and their corresponding weights. The characteristic parameter here refers to the representative parameter which can describe an oil or gas reservoir. Apart from representativeness, attention should be paid to avoiding repetition or correlation across the selected parameters.
(3) As the model evaluation standard is established for complex fault-block oil reservoir, the total weights of the characteristic parameters related to structural model should not be less than one quarter of the total score, that is, 25 points.
(4) Following determination of the characteristic parameters and their weights, we accordingly set the evaluation threshold values of each characteristic parameter, and subsequently obtained the final evaluation result based on the cumulative score, which is typically categorized into three levels, that is, low, medium and high level.
2. Testing approach and characteristic parameter
2.1. Data verification
2.1.1. Verification methods
The most direct verification is by means of hard data, which are usually divided into four categories: (1) New well test. (2) Blind test. Blind tests can be representative and convincing, provided that blind wells are distributed evenly and comprise cored well(s). (3) Well performance test. The injection-production response is the special case. (4) Numerical simulation test. The quality of static model is evaluated according to the initial fitting error in history matching[4-5,10]. Generally, the first two belong to static methods, which are comparatively rapid and straightforward, but lack of representativeness due to local tests, whereas the latter two are dynamic methods. Although the representativeness of the third method is somewhat improved, it just keeps reservoir connectivity in view. The advantage of the forth method is that it involves a great number of wells and is therefore deemed to be more representative; however, it is time consuming. As a result, it is wise to use the four methods comprehensively.
Moreover, streamline simulation falls into the forth category, and has been widely utilized in recent years[4,5], because it does not necessarily coarsen the model, instead, with given fluid parameters, it can quickly model the flow path of the injected fluid based on the reservoir heterogeneities of the existing model, and perform a rapid assessment in combination with the injection-production response in the oilfield. As for “the consistency check of probability distribution”, an approach to examine if the final model honors the frequency statistics from the well-log data, strictly speaking, it is not the quality evaluation of the final model despite using hard data. On the country, it is just an important step during quality control, and an essential procedure for developing a high-quality model[13].
2.1.2. Characteristic parameters and their weights
Data verification is subdivided into the static and the dynamic. Six characteristic parameters were selected in this study, including five static parameters (complex fault contact relationship, target zone depth, lithofacies and depositional facies, net pay and permeability), and one dynamic parameter (initial fitting error of water cut). This may be attributed to the following:
Two characteristic parameters regarding structural model are the complex fault contact relationship and the depth prediction of target zone[14,15]. Faults not only determine reservoir compartmentalization, but impact fluid flow in the reservoir. At the development stage of oilfields, low-grade faults have been increasingly drawing attention[16,17].
The characteristic parameter selected in facies modeling is the lithofacies or depositional facies, which can be described as lithologic units that include a series of geological characteristics. Facies model can be considered as an elementary component of reservoir model[18], because facies are highly linked with the petrophysical properties that directly determine the hydrocarbon pore volume and fluid flows[19].
Two characteristic parameters selected in property modeling are net pay and permeability. Net pay is a critical parameter of reserves estimation, typically in the form of NTG ratio in the model. In addition, the goal of drilling campaign is to find oil-bearing layers as thick as possible. Hence, it is of practical significance and commercial value to take net pay as a characteristic parameter. Permeability is the most direct parameter dictating the ease of fluid flow and ultimate recovery. Nevertheless, its range of variability is the largest[20], so it is the most difficult to predict.
The characteristic parameter in the numerical model is the initial fitting error of water cut. The data to be fitted in history matching frequently include pressure, fluid production rate, oil production rate, and water cut of the oilfield or single well, and the emphasis is to fit initial water cut and primary variables during the late period of production history[21].
The above six characteristic parameters are all important for quality evaluation of geological model based on real data. Consequently, according to the opinions of 10 experts, the weights of them were equally given 10 points.
2.2. Geological understanding
Comprehensive geologic studies play the core role in reservoir modeling[22]. Therefore, the final static model should reflect the prior understanding and replicate the geologic reality[23,24]. Two characteristic parameters, namely the variogram parameter selection and the final static model selection, were chosen according to the following reasons:
Different geostatistical techniques have seen an extensive application in 3-D geologic modeling in recent years[25,26,27]. Geostatistical simulation algorithms are mostly grouped into two families: variogram-based techniques and variogram-free techniques. It is reported that almost 90% of the reservoir-characterization studies use variogram-based geostatistical techniques to create a 3D model[26]. Proper selection of variogram parameters (range, nugget, azimuth, etc.) is a key to obtain a geologically sound reservoir-characterization model[5,28]. Unfortunately, variogram modeling and interpretation are often performed hastily or even skipped altogether. Considering that it is interrelated to the already selected characteristic parameter, i.e., lithofacies or depositional facies, its weight was assigned 5 points.
The final static model selection is a characteristic parameter which can fully express the geological understanding accomplished in the early phase of study. The original oil in place (OOIP) is conceived as one of the most important geological insights. Under the same condition of hard data and geological understanding, if the modeling methods are appropriately employed, the P50 reserves (the corresponding reserves at 50 percent of the cumulative probability, also known as probable reserves) derived from stochastic simulation should be equal to or close to the prior reserves in the deterministic method; the prediction error should be commonly no more than 10%[6]. If the inference bias is too large, it is likely that there is a problem of selecting calculation parameters or modeling methods[4], because both methods use the volumetric method and evaluate reserves on the basis of average values: all the calculation parameters in the deterministic method are taken as the arithmetic mean, and P50 itself is median probability usually used as the base case of geological reserves in the probabilistic method[29]. The relative error of reserves estimation has a veto on the evaluation of model quality, so the maximum weight, 15 points, was determined among all characteristic parameters.
For exploration and production, probabilistic methodology has more advantages over deterministic methods as to reserves estimation, partially because the former adequately considers the uncertainties of calculation parameters through statistical tools, which leads to a range of reserves rather than a fixed value, and avoids false precision[30]. The reserves estimation obtained by probability calculation is more comprehensive and able to better assess reserve risk[29,31]. However, it does not mean that P50 reserves are more dependable than the prior reserves. This is a comparison of two methods, i.e., probabilistic method and deterministic method, instead of a contrast between two numbers. Furthermore, the selection of final static model should take integration of dynamic examination into account[27].
2.3. Process check
To assure reliability, the systematic quality evaluation should not only emphasize the result validation, but also value the process check, that is, the quality control of important steps during the modeling process. We adopted spot check to make the evaluation system simple and practical. The selected five characteristic parameters in this study include grid design, facies modeling method, seismic constraint, saturation calculation method and reserve impact factor analysis. The selection reasons are listed as follows:
Grid is the minimum description unit of model and the foundation of modeling. The grid boundary, size, direction and trend are defined according to study purpose and project area. It is significant to check the number of irregular grids near faults, examine whether there exist intersections between upper and lower grids, and whether the grid cell is negative. Weight it by 5 points.
Facies modeling is a crucial part of reservoir modeling. It usually requires researchers to analyze the adaptability of modeling techniques and to attempt to use some innovative or integrated approaches. In view of importance and time cost, this characteristic parameter was weighted with 7 points.
With limited well control, it is important to use seismic data to constrain models, which contributes to improving the model quality to a large extent[24,32-35]. The integration of seismic inversion results in property modeling is now common practice[36]. The weight of seismic constraint is 4 points.
It is necessary to examine the modeling methods of initial water saturation, because the spatial distribution of this petrophysical property is controlled by gravity in a reservoir, in which the initial water saturation gradually decreases from the free water level up to a given height of oil column[37,38]. The saturation calculated with the capillary pressure is very close to the one from sealing core analysis[39]. Therefore, the capillary pressure method, the J-function method or the saturation height function method should be preferred in massive reservoirs with distinct transition zone. The saturation calculation method weights 2 points.
Uncertainty in reservoir characterization and modeling is caused by the uncertainty of input data and the uncertainty in the inference. Uncertainty analysis, therefore, should include studies of data inaccuracies and inference uncertainty from data to estimation of reservoir properties[40]. Inference uncertainties usually include conceptual, interpretational, and methodological uncertainties. It is more straightforward to assess uncertainties of some “composite” reservoir variables, such as hydrocarbon volumetrics, using stochastic simulations[40]. Uncertainty analysis is an integral part of high-quality modeling and also a research trend, which is in general moving away from an “honor the data” paradigm to an “honor the data and respect/incorporate uncertainty” paradigm[41]. Chinese scholars should pay enough attention to it. The weight of reserves impact factor analysis is 2 points.
In summary, 13 characteristic parameters were selected altogether from data verification, geological understanding and process check, among which the cumulative weights of parameters related to structural model amount to 25 points (including 20 points from data verification and 5 points from process check), meeting the requirement of the third item in the evaluation strategy.
3. Evaluation standards
The three-level threshold values of each characteristic parameter need to be optimized when the standard is initially formulated for a certain type of reservoir in a given region at a particular stage, so as to avoid losing the significance of relative evaluation if the standard is too rigorous or too loose. Hence, it is desired to firstly estimate the prediction difficulty of a given characteristic parameter according to data quality and subsurface heterogeneities, and then refer to industry standard, the precision level of analogies and work experience, and finally use in-situ data to determine suitable threshold values through trial and error. In the following case, for the reservoir at a depth of -1 400 m with a well spacing of 300 m, the accuracy standards of well-top prediction vary from the data condition with to without 3-D seismic survey. If available, the average absolute error of less than 1 m can be set as high level; if not, less than 2 m works. Similarly, in an attempt to amplify the differences of the three-level evaluation results, the evaluation standard of each characteristic parameter is established as full score, half score, and one point or zero point for high, medium, and low level respectively. The final evaluation result is grouped by the cumulative score into three levels: high level when the score is greater than or equal to 80 points, medium level if the score lies between 60 and 79 points, and low level as the score is less than 60 points.
The evaluation standard of characteristic parameter is not invariable in different development phases. For example, in the conventional water-flooding sandstone reservoir of the western Zone 7 in Gudong Oilfield, the reservoir engineers statistically analyzed the water-cut fitting errors of 312 wells at the low-medium water-cut stage and that of 420 wells at the high-extra high water-cut stage separately, and studied the adaptability of evaluation criteria[10]. At the low-medium water-cut stage, due to the rapid rise of water cut, the variability of water cut is large. So is the fitting error. For instance, there were only 54.5% of wells with a relative fitting error of less than 5%, whereas there were 86.5% of wells with that of less than 10%. Obviously, it is too strict if the error of less than 5% is taken as the standard of high level, and it is appropriate to take relative error of less than 10%. By contrast, at the high-extra high water-cut stage, the variability of water cut is relatively small, and so is the fitting error. The number of wells with a relative fitting error of less than 5% accounts for 89.5%, while the number of wells with that of less than 10% does 97.4%. Apparently, it is too loose if the error less than 10% is regarded as the standard of high level, and it is suitable to take relative error of less than 5%. Similarly, as far as the cumulative score is concerned, the threshold values of three- level evaluation also vary from different development stage.
On the basis of the 13 characteristic parameters and their weights, we generated the quantitative evaluation standard of 3-D geological models for complex fault block reservoirs and presented a case (Table 1).
Table 1 Quantitative Assessment Standard of 3-D Geological Models for Complex Fault-block Oil Reservoirs and a Case.
| Category | Characteristic parameter | Weight assignment | Assessment standard | Case score | ||||
|---|---|---|---|---|---|---|---|---|
| Low | Medium | High | ||||||
| Data verifi- cation (60 points) | Static data | Structural model | Contact relationship of complex faults | 10 | Unreasonable or over- simplification. 1 point | Basically reasonable, or fault surfaces are constructed without seismic constraint. 5 points | Reasonable in space or arbitrary section. Surfaces are guided by fault sticks from seismic interpretation. 10 points | 10 |
| Layer depth of target zone | 10 | Mean absolute error >2 m. 1 point | Mean absolute error is 1-2 m. 5 points | Mean absolute error <1 m. 10 points | 10 | |||
| Facies model | Lithofacies or depositional facies | 10 | Mean relative error >20%. 1 point | Mean relative error is 10%-20%. 5 points | Mean relative error <10%. 10 points | 10 | ||
| Property model | Net pay | 10 | Mean relative error >30%, 1 point | Mean relative error 10%-30%, 5 points | Mean relative error <10%, 10 points | 10 | ||
| Permeability | 10 | Mean relative error >80%. 1 point | Mean relative error is 40%-80%. 5 points | Mean relative error <40%. 10 points | 10 | |||
| Dynamic data | Reservoir numerical model | Initial water- cut fitting error | 10 | The number of wells with a relative error of less than 5% <60%. 1 point | The number of wells with a relative error of less than 5% accounts for 60%-90%. 5 points | The number of wells with a relative error of less than 5% >90%. 10 points | 5 | |
| Geological understanding (20 points) | Variogram parameter selection | 5 | When sample points are few and disorder, analog data are not used. 1 point | Analog data are used when sample points are sparse. 3 points | Due to sufficient sample points, the automatic fitting rate is higher and the law is clear. 5 points | 5 | ||
| Final static model selection | 15 | The relative error of OOIP >10%. 1 point | The relative error of OOIP is 5%-10%, or not performing dynamic test. 8 points | The relative error of OOIP <5%, honoring production performance. 15 points | 15 | |||
| Process check (20 points) | Structural model | Grid design | 5 | Many irregular grids around faults, or intersection between layers, or negative grid cell volume, etc. 1 point | Few irregular grids around faults, no intersection between layers, and no negative grid cell volume, etc. 3 points | Reasonable grid design and no abnormal case in arbitrary section across faults. 5 points | 5 | |
| Facies model | Facies modeling method selection | 7 | Just apply a deterministic method. 1 point | Arbitrarily use a stochastic approach without any analysis. 4 points | Investigate several modeling techniques and select the most suitable one. 7 points | 7 | ||
| Property model | Seismic constrain | 4 | For area with limited well data, seismic constraint is not integrated without interpreting reasons. 1 point | Seismic data are not available or poor link between seismic attributes and well data. 2 points | Owing to relatively high correlation, seismic constraint is incorporated. 4 points | 4 | ||
| Saturation calculation method | 2 | Kriging interpolation according to well data. 0 point | Derived from porosity log without allowing for transition zone. 1 point | Considering transition zone, capillary pressure method or saturation-height function method is thus used. 2 points | 1 | |||
| Uncertainty analysis of the model | Sensitivity Analysis on reserves | 2 | No any analysis. 0 point | Qualitative analysis. 1 point | Quantitative uncertainty analysis in form of probability distribution, and rank by weights. 2 points | 0 | ||
| Cumulative score | 100 | 11-59 | 60-79 | 80-100 | 92 | |||
4. A case study
4.1. Reservoir features
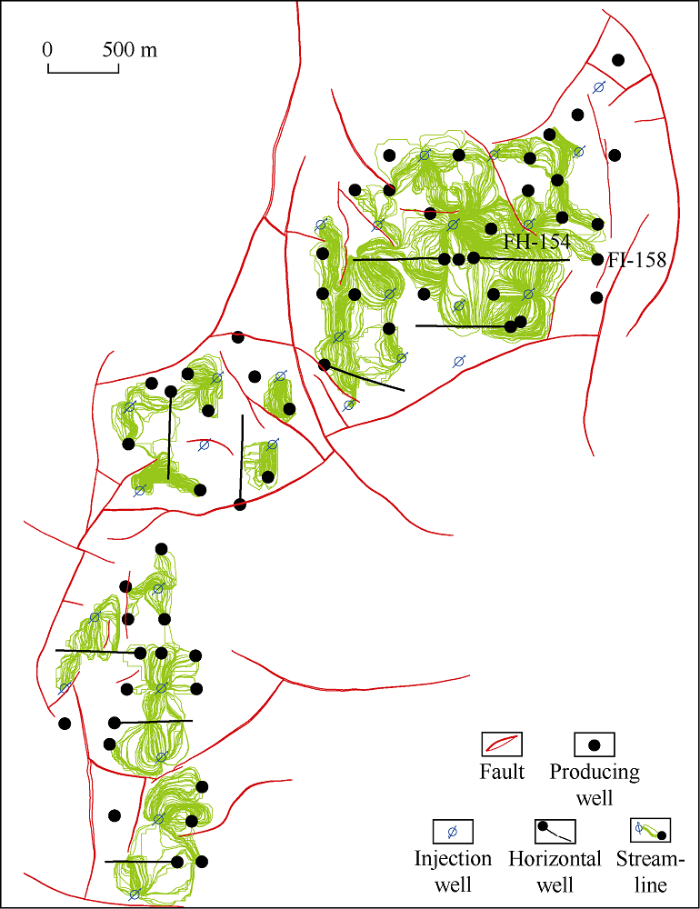
Block F, located in the south of Songfangtun Oilfield in Daqing, China, is a typical complex fault-block sandstone reservoir (Fig. 1). It is characterized to be a monocline plunging towards north east as a whole and a series of low relief structures are generated inside. The producing zone is the lower Cretaceous Putaohua oil layers in Segment 1 of Member Yaojia at a depth of 1 330-1 430 m. The reservoirs principally consist of delta front sandbodies and Putaohua oil layers is vertically divided into 13 units. The rock properties are marked by medium porosity and medium to low permeability. Porosity ranges from 12% to 26% and on average 18%. Permeability is (3.47-401.52)×10-3 μm2, on average 10.29×10-3 μm2. Block F was put into production in February, 2007, adopting a 300 m×300 m inverted seven-spot water flooding pattern. By the end of 2015, 56 producing wells and 29 water injection wells had been drilled. The recovery factor of Block F was 14.6%, the annual production rate was 1.08%, and the total water cut was 67.5%.
Fig. 1.
Fig. 1.
Top structure of Putaohua oil layers in Block F.
A wide variety of data were available in this case, including 85 well logging data and test data, 3 core well data, 3-D post-stack seismic data, and top structural map of Putaohua oil layers as well as production data.
4.2. Quantitative assessment
According to the evaluation criteria, the 13 characteristic parameters were measured item by item, and the final model scored 92 points out of a possible 100 (Table 1). The deduction items and the full score items were analyzed as follows:
4.2.1. Deduction item analysis
In terms of single item score (Table 1), there are three items deducted, including the initial water-cut fitting error (5 points), the saturation calculation method (1 point) and the reserve impact factor analysis (2 points).
The statistical results show that, among 54 producing wells, the number of wells with the water-cut fitting error of less than 5% accounts for 64.8%,. According to the evaluation standard, it belongs to medium level, so 5 points are deducted.
Without applying proper approaches to deal with the oil- water transition zone caused by low permeability, the saturation models were generated just by carrying out the Sequential Gaussian Simulation (SGS) according to the initial water saturation derived from porosity above oil-water contact, which was of medium level, so 1 point was deducted.
After reserves estimation and model selection, sensitivity analysis or impact factor analysis on reserves was not performed unfortunately, and 2 points were thereby deducted.
The first deduction is normal in consideration of its prediction difficulty. However, the latter two should have been avoided. The problems occurred because the geo-modelers had not paid enough attention to the technical development and research trends in the field of geologic modeling.
4.2.2. Full score item analysis
One case was selected from each part of assessment system (data verification, geological understanding and process check) and analyzed, that is, the complex fault contact relationship, the final model selection and the facies modeling method selection respectively.
4.2.2.1. Complex fault contact relationship
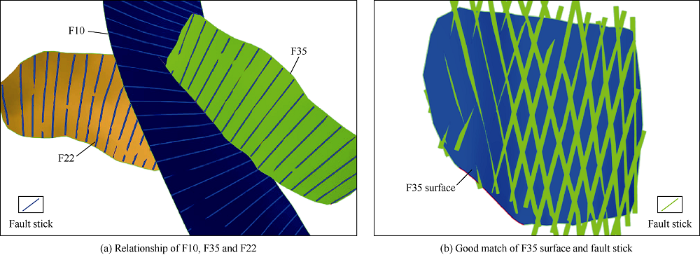
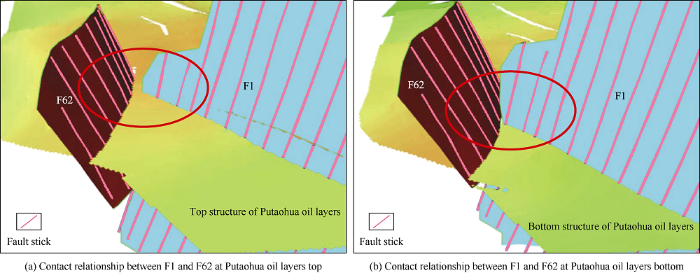
Checking the contacts between faults, especially complex faults, is one of the major issues to evaluate the model quality of complex fault-block reservoirs. The X-shaped faults was checked firstly in this case, involving three faults such as F10, F35 and F22 (Fig. 1). The model reveals that the generated faults clearly exhibit the shapes of fault surfaces and the fault contacts (Fig. 2a), and the fault surfaces also maintain consistency with the fault sticks of seismic interpretation (Fig. 2b). Secondly, the contact relationships were investigated between faults and stratum. There are two faults, namely F1 and F62 (Fig. 1), which do not intersect at the top of Putaohua oil layers (Fig. 3a), but cross at the bottom (Fig. 3b). This detail was reproduced in the model. Based on above analysis, a conclusion is drawn that the fault contacts are reliable. Consequently, this item was given full score.
Fig. 2.
Fig. 2.
X-shaped fault contact relationship.
Fig. 3.
Fig. 3.
Fault-Fault-Stratum contact relationship.
4.2.2.2. Final model selection
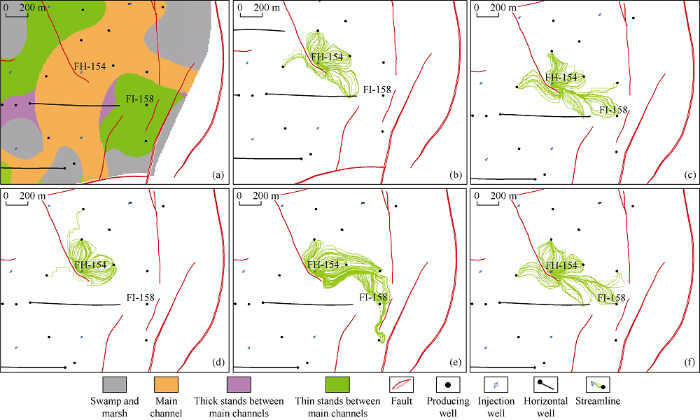
The final model selection is a characteristic parameter that can comprehensively incorporate the geological understanding, as discussed previously. Only when selecting a geologic model with relatively small error of the prior reserves, can one profoundly perceive the essence of geological understanding. Besides, the selected model is required to honor the oilfield’s production performance[27]. A total of 50 realizations of equal probability were generated with the stochastic simulation technique. P50 reserve was obtained by running Monte Carlo simulation, to recognize the 23rd case which corresponds to P50 value. Other four realizations (corresponding to the 38th, 32nd, 16th and 42nd; the former two are slightly smaller than P50 and the latter two are marginally larger than P50) were also selected, and then the final model was screened out by streamline simulation. As a rule, the streamline density is strongly correlated with sweep coefficient of water flooding[42], regarded as an important factor to judge well-control degree and interwell reservoir connectivity. The geo-modelers compared the five corresponding streamline simulations.
On the whole, it is considered that the flow characteristics of the 38th realization can explicitly incorporate the injection-production status in the north, center and south. In other words, the streamlines of the 38th realization nearly cover the northern production area, implying interwell reservoirs are well connected, and the well pattern is relatively reasonable; the sparse streamlines in the central production area indicate the reservoir connectivity gets worse and the efficiency of water flooding is unsatisfactory; the situation of the southern production area lies in between (Fig. 4).
Fig. 4.
Fig. 4.
Streamline model of the 38th realization in Block F.
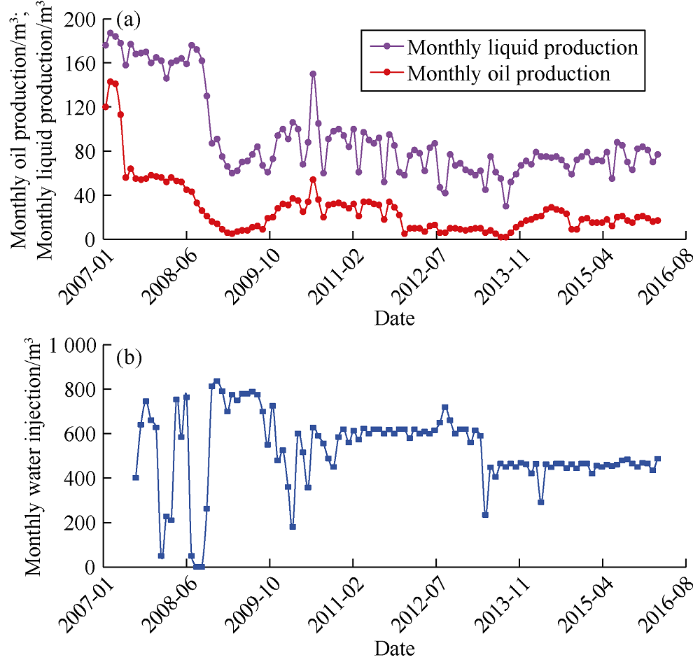
In terms of local region, the trend of the production curve of Well FI-158 is in overall agreement with that of the injection curve of Well FH-154, showing that the reservoir connectivity is pretty good between two wells (Fig. 5). The streamline model of the 38th case better captured the injection-production response because its flow path properly matches the shape of the main river channel (Fig. 6).
Fig. 5.
Fig. 5.
Production curve of Well FI-158 (a) and injection curve of Well FH-154 (b).
Fig. 6.
Fig. 6.
Local facies map of Unit PI41 and streamline models of 5 realizations. (a) Local facies map of Unit PI41; (b) the 16th; (c) the 23rd; (d) the 32nd; (e) the 38th; (f) the 42nd.
In a word, the 38th realization is the optimal static model. The estimated reserves are 242.7×104 t; the relative error is -1.5% compared with the prior calculation (246.4×104 t). As a consequence, this item acquired full score, 15 point.
4.2.2.3. Facies modeling method selection
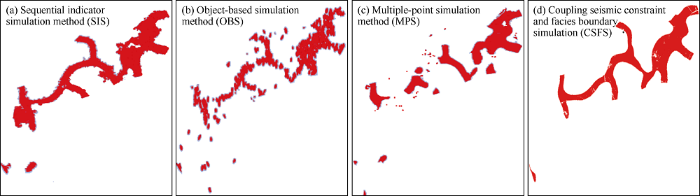
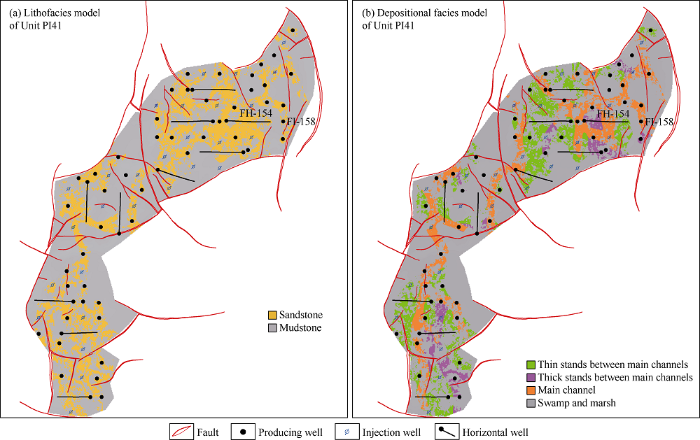
Efforts were made to investigate four facies modeling approaches undertaken to characterize the main river channels in this case, including sequential indicator simulation (SIS), object-based simulation (OBS), multiple-point simulation (MPS), coupling seismic constraint and facies boundary simulation (CSFS). The result suggests that the river channel’s continuity simulated by the SIS method can meet requirement (Fig. 7a). The OBS method is very flexible in terms of replicating complicated channel’s geometries, but fails to honor well data completely (Fig. 7b); the MPS method allows for replication of complex geometries of main channels more than channel’s continuity, which leads to a remarkable difference between the output and the underlying reservoir geology (Fig. 7c). The CSFS method integrates seismic constraint and facies condition into the sequential indicator simulation, and a blind test demonstrated it could honor common geologic principles horizontally and facies recognition from well logs vertically with a smaller error compared with SIS (Fig. 7d). Additionally, the computation speed is listed from fast to slow as follows: SIS, CSFS, OBS and MPS. As such, the CSFS method is believed to be the optimum technique to build the lithofacies model and the depositional facies model for study area (Fig. 8).
Fig. 7.
Fig. 7.
Comparsion of four facies modeling methods especially for main channel.
Fig. 8.
Fig. 8.
Lithofacies model (a) and depositional facies model (b) for Unit PI41 with the CSFS method.
5. Conclusions
It is the traditional way of thinking without differentiating reservoir types that limits the establishment and development of the quantitative evaluation criteria of 3-D geological model. If we reduce the scope of evaluation to the same reservoir type, or even to the same research target, the feasibility of the quantitative assessment will be present.
The quantitative evaluation system comprises three main parts, namely, data verification, geological understanding and process check. The precise result is undoubtedly to be expected, but the sound process should also be emphasized. Apart from representativeness, care should be taken to avoid repetition or correlation across characteristic parameters; the three-level threshold values of each characteristic parameter need to be optimized, lest the standard lose the significance of relative evaluation if it is too strict or too loose.
As the quantitative assessments of 3-D geological model are still experiencing with ongoing research, some key factors affecting the quality of models are not involved in the system, such as the reliability of input data mentioned previously. In practice, quantifying the evaluation of input data can be a real challenge because it belongs to another dimension in terms of current characteristic parameters. How to address this issue needs further studies.
Reference
Quality control of static reservoir models
Integrated 3D reservoir interpretation and modeling: Lessons learned and proposed solutions
DOI:10.1190/tle32111340.1 URL [Cited within: 2]
Quality control and checking method of reservoir geological model
Reservoir geological model is a 3D gridding data volume describing the geology characteristics and reservoir property.Geological modeling with high quality is the key of reservoir fine management and high-efficiency development.This paper analyzed the main influence factors of geological model quality,and put forward the quality control and the checking method of geological model during the process of modeling.According to the normalized process of geological modeling,the logical errors between basic data were checked up to verify the accuracy of data and to check the consistency of drilling data and structural model.The structure model was contrasted to decide the quality of structure model,the height,volume,distortion of every grid were analyzed and the consistency of statistics discipline between log interpretation data and attribute model was analyzed to control the quality of attribute model.The reliability of geological model was checked by the method of decreasing wells and history matching.Field application shows that the quality of geological model and the history matching accuracy are improved greatly by controlling and checking the quality of reservoir geological model.
The keys to quality control of 3-D reservoir modeling
QC methods and application of 3D geological modeling
Based on the workflow of geological modeling, QC methods of geological modeling were summarized. The basic data preparation and QC, structural modeling QC, facies modeling QC, properties modeling QC, and model validation are five main QC steps. Application of these QC methods in projects shows that these QC methods can significantly improve qualities of geological modeling.
Strategy of reservoir geological modeling and application of technical method
3D quantitative geological models could indicate the spatial distribution characteristics and change laws of geological properties and offer the geological references for reservoir exploitation. Aimed to actual geological states in the west of China, some technical thoughts about geological modeling were put forward. On the basis of analyzing the application effect of the hierarchical modeling strategy, the variogram range parameters of the sedimentary micro-facies and reservoir properties, which could present the spatial heterogeneity of geological variables and could be used in the subsequent course of controlling the properties modeling, are calculated by the mathematic tool of variation function analysis. And the reasonable rules of classifying and incorporating micro-facies are determined by contrasting and analyzing the effects of different modeling methods which could influence the growing of sand body and embody the effects from the facies-controlled modeling. Finally the models including structures, architecture of sandbody, sedimentary facies and reservoir properties are established by combining the determinate modeling methods such as Co-kriging with stochastic modeling methods such as Sequential Gaussian Simulation(SGS). Aimed to the indeterminate models from stochastical modeling, the methods are presented to validate the geological models including comparing conceptual geological distribution and statistical characteristics, testing rarefied data and analyzing the distribution law of the probable reserves. And then, the accuracy of the geological modeling technique and predictability of the geological models are demonstrated.
Quality evaluation and control method research on geological models
Quality evaluation method for geological model based on reservoir numerical simulation
Research achievements on reservoir geological modeling in the past two decades
A quantitative oil and gas reservoir evaluation system for development
DOI:10.1016/j.jngse.2017.02.026
URL
[Cited within: 1]

61Identified factors and characteristics influencing reservoir quality.61Identified factors influencing input data quality.61Developed a quantitative evaluation system to measure oil and gas reservoir readiness for development considering both reservoir quality and data quality.61Conducted case study to verify developed system.61Provided best practice to evaluate project with evaluation systems.
Frequentist meets spatialist: A marriage made in reservoir characterization and modeling
DOI:10.1016/j.biortech.2007.04.019 URL [Cited within: 1]
Geological modeling difficulties and countermeasures of complex fault- block reservoir
At present,the accurate and quantitative characterization of complex fault-block reservoir is the difficulty and research hotspot for reservoir geological modeling.In this paper,taking the geological modeling of complex fault-block reservoir for Z il group of Kong 1 Member in Zaobei Area,Zaoyuan Oilfield as an example,based on the data such as geological research,log and seismic interpretation,using RMS software and combining the modeling technique of RMS with basic geological research,the corresponding research countermeasures are put forward according to the difficulties of structure modeling,micro-facies modeling and attribute modeling.Based on the methods,it turns the geology understanding into constraint condition accurately.It also uses many ways to check and correct the model to make sure that the model is according with the underground geological conditions.The difficulties of reservoir modeling are resolved effectively.The stochastic modeling precision of complex fault-block reservoir is improved.The model can provides reliable geology basis for the further numerical modeling and the exploration of potential target in study area.
Application of geological modeling technology in secondary development of old and complex fault block oilfields
Progress and prospects of reservoir development geology
DOI:10.1016/S1876-3804(17)30069-1
URL
[Cited within: 1]

This paper deals with the main scientific problems, academic connotation, progress and prospects of reservoir development geology. The reservoir development geology involves the key scientific problems of reservoir connectivity, flow ability, and changeability through time. Its research focus on the forming mechanism and distribution model of geological factors controlling the reservoir development, the control mechanism of geological factors to oil and gas production, the rule of reservoir dynamic evolution during development, and the reservoir characterization and modeling technology. Important progress has been made on theory and technology of reservoir development geology in high water-cut reservoirs, low permeability and tight shale reservoirs, fracture-cavity reservoirs, which makes the reservoir development geology grow as an independent academic subject already. With the development expansion in areas of deep-strata, deep-water, and unconventional hydrocarbon reservoirs, and the increasing difficulties of high water-cut reservoir development, the theory and technology of reservoir development geology remain to be developed in order to support efficient and economic development of hydrocarbon fields with a sustainable growth.
Application of farewell fault detection technology to the polymer adjustment in complex fault block reservoirs
The southern district of Gudao Oilfield is a heavy oil and sparse sandstone reservoir,which is complicated by faults,and has complex geologic conditions.13 faults separate the whole district into 11 blocks,and every block has its own oil and water system,which brings bad effect on polymer flooding.In order to recognize the rupture system,adjust the injection-production corresponding relation and improve the effect of polymer flooding,the technologies of small wave and more scales test and coherence analysis are used to explain farewell faults,and the distribution map of the faults is redrawn in the south district.The methods of interference test and performance analysis are employed to test the veracity of the new rupture system.Based on above,the injection-production corresponding relation is adjusted,with the polymer flooding effect improved.
Fully integrated hydrocarbon reservoir studies: myth or reality?
DOI:10.3844/ajassp.2010.1477.1486 URL [Cited within: 1]
Integrated reservoir modeling of a Pinedale tight-gas reservoir in the Greater Green River Basin, Wyoming
Geological Models of Petroleum Reservoir
Recently, to build a quantitative geological model'of reservoir has been much concerned in the research of reservoir description, while the description of 3-dimensional, spatial and quantitative distribution of the permeability within a reservoir model are the key factor to be studied. Three types of model; conceptual model, static model and predictable model with different accuracy and is used at different stages of reservoir development according to their requirement.
Greeting the great development of theories and applications of reservoir modeling
DOI:10.1016/S1872-5791(08)60035-4
URL
[Cited within: 1]

The Chifeng region is located in the southeastern part of Inner Mongolia, North China. It spans both the metallogenic belts of the Greater Xing'an Mountain and the Yin Mountain. Because of the unique metallogenic background, the Chifeng is a region of high nonferrous metal mineral potential in China. In this article, multisource data sets including geological, geochemical, gravity, airborne magnetics, and Landsat ETM+ data were integrated for mineral potential mapping by using GIS technology. Under the guidance of regional metallogenic regularities and the application of the geoanomaly ore forming theory, nine diagnostic deposit recognition criteria layers were extracted from those sets. Furthermore, these deposit recognition criteria layers were combined in the weight of evidence (WolE) model, which used the spatial correlations between the evidence layers and the known mineral occurrences, to calculate the posterior probability and indentify the delineated prospective area. The results showed that there were three NE-SW trending prospective belts in the north of Chifeng, and one NW-SE striking favorable ore-forming belt in the south of this region. Eighty-six percent of the known mineral occurrences containing 95% of the mount metal resources fell in these four belts. The authors carried out further research study and provided references for resource prediction and assessment study in this area. The results offered scientific evidence of resource exploration in the Chifeng region.
Geological constraint principles in reservoir stochastic modeling
The principles of geological constraints on reservoir stochastic modeling are discussed. In order to decrease the uncertainties in simulation realizations, the following geological constraint principles must be abided: ①equivalent\|time constrained modeling; ②origin\|controlled modeling; ③multi\|stage modeling; ④choosing optimum stochastic simulation methods using geological model; and ⑤determining statistical character parameters using proto\|model. A new flowchart of reservoir stochastic modeling under geological constraints is proposed. A case study of stochastic modeling of Chang 6 reservoir of Triassic in Pingqiao horizontal well region of Changqing oilfield is used to further certify the methods of geological constrained stochastic modeling.
Seismic integration for better modeling of rock type based reservoir characterization: A field case example
Coupling spatial and frequency uncertainty analyses in reservoir modeling: Example of judy creek reef complex in Swan Hills, Alberta, Canada
Stochastic modeling for characteristics of petroleum reservoir constrained by facies
We present a stochastic modeling for characteristics of petroleum reservoirs constrained by facies to yield results coincided with real geological setting. The facies acting as the constraint are based on known geological data and include depositional microfacies such as an extension direction and a ratio of width to thickness of microfacies. A strategy of the reservoir modeling controlled by facies is as follows: scale differences of reservoir controlled by hierarchy for multi-depth levels along vertical direction; for each depth level, plane zone differences of reservoir managed with nested structure. The constraints are exerted by the following three aspects: combining the order of facies, probability correlation and quantitative geological knowledge database or variogram to constrain heterogeneities of petroleum reservoir. The modeling constrained by facies is characterized by depositional formation and genetic evolution used for as guidance of the modeling, use of coordination of multi-parameter and constraint by hierarchy, full use of horizontal distribution and vertical evolvement of depositional facies belts as constraint boundary. The geological and drilling data in Baolige oil fields in Inner Mongolia, North China are used to check and optimize the method. Results show this optimized modeling can indicate heterogeneity and connectivity distribution of subsurface reservoirs, and have been confirmed by new wells in Baolige oil fields.
Application of the stochastic method to oil and gas reserves estimation
DOI:10.3787/j.issn.1000-0976.2009.11.026
URL
[Cited within: 2]

Reserve estimation is one of the most important parts of reservoir exploration and development,and is also the basis of development policy and plan making.Currently,for reserve estimation,there are volumetric method,analogy method and material balance method.Compared with the other two,the volumetric method shows a better suitability,which includes two numerical methods,i.e.deterministic and stochastic in parameter determination.Hereby,the differences of calculation concept between the deterministic method and the stochastic method were compared firstly.Then,geological reserves were estimated as a practice using the deterministic method and the stochastic method respectively.Analysis and results show that arithmetic mean values are applied to all the physical property parameters by the deterministic method,while for the stochastic method,probable distribution function of the calculated parameters is determined and then reserves corresponding to different probability are obtained through multiple iterations of Monte Carlo simulation.Compared with the deterministic method,calculation results show that the stochastic method which can offer a series of reserves based on varying risks,thus better assessing reserve risks can supply a better reference for the investment decision-makers.
Measuring what we think we have found: Advantages of probabilistic over deterministic methods for estimating oil and gas reserves and resources in exploration and production
DOI:10.1306/08030606016 URL [Cited within: 1]
Calculation of probabilistic reserves of reservoir with stochastic modeling method
DOI:10.1109/CVPR.2005.231
URL
[Cited within: 1]

The uncertainties of a gas reservoir located in the north part of Shaanxi Province were studied with stochastic modeling. The responding gas reserves of the reservoir were calculated with three groups of data obtained from two hundreds and fifty four wells, one hundred and forty six wells, thirty wells by using fifty, one hundred and two hundreds of random seeds, respectively. Probabilistic distributions of these reserves were analyzed. Three probabilistic reserves (P90, P50, P10) for the three groups of data were obtained respectively by using one hundred of random seeds. The probabilities of three probabilistic reserves larger than the real reserves are 90 percent, 50 percent and 10 percent respectively. The calculated results illustrate that as the number of wells increase, the mean values of gas reserves continuously increase, and their mean variances decrease, which results in the reduction of the uncertainties of reservoir. The top strata surface and net thickness were obtained by Kriging method. The spatial distributions of porosity, permeability and gas saturation were obtained by simulation of Gaussian field.
Use of a seismic derived constraint: Different steps and joined uncertainties in the construction of a realistic geological model
Petrophysical seismic inversion to determine more accurate and precise reservoir properties
Geological modeling technique for reservoir constrained by seismic data
The reservoir geological modeling using seismic data was defined as reservoir geological modeling constrained by seismic data.The significance of this technique,function of seismic data in constraining reservoir geological modeling,difference of this method with seismic inversion,domain of application and methods for building reservoir geological model were discussed in detail.The case study shows that uncertainty of reservoir geology models can be reduced by integrating seismic data,and precision of these models can be improved.
Integrating seismic data in reservoir modeling: The collocated Cokriging alternative
Seismic reservoir characterization: An earth modelling perspective
Application of saturation-height functions in integrated reservoir description
Feasibility analysis of calculating original saturation of oil reservoir by using J-function
Evaluation on oil saturation of carbonate reservoir in H Oilfield using capillary pressure and logging data
Archie equation provide basis for calculating reservoir oil saturation using logging data.Reasonability of its lithoelectric parameters directly influence the calculation accuracy of oil saturation,and even the result of reservoir evaluation.Comparison analysis shows that,different experimental methods and processes and manmade error lead to different lithoelectric parameters with two experiments for a core from a same horizon in a same laboratory.Thus oil saturation evaluation with lithoelectric parameters got from lithoelectric experiment needs other data to examines its reasonability.In the condition without sealed coring,oil saturation determined by capillary pressure data can be used as a standard to examine and optimize lithoelectric parameters so as to get reasonable oil saturation of reservoir.Evaluation on carbonate reservoir increases accuracy of oil saturation interpreted by logging data.
Uncertainty analysis in reservoir characterization and management: How much should we know about what we don't know?
DOI:10.1306/13301404M963458 URL [Cited within: 2]
Flow characteristics and productivity of fractured horizontal wells based on streamline
DOI:10.3863/j.issn.1674-5086.2010.05.020
URL
[Cited within: 1]

Injection and fracturing make the seepage in low permeability reservoir more complex.In order to visually reflect the flow characteristics of fractured horizontal wells,the streamline simulation method is used to investigate the regulations of fractured horizontal wells,such as:streamline distribution,productivity of different fractures and effect of fracture length on the development.Fractured horizontal well with spindle-type is designed.Streamline simulation has shown that:streamline distribution in the region between injection well and fracture at the end of horizontal well is more intensive than that of other regions;among the three fractures,the one at the end of horizontal well receives the vast majority of streamlines,only few flow into the middle fracture.Productivity(including oil and liquid) in fractures at the end of horizontal well is higher than that of the middle fracture.Early water breakthrough and sharp water rising lead to rapid increase of water cut for fractured horizontal wells.Compared with general fractured horizontal wells,the streamline in spindle-type is more uniform,which can enhance oil recovery by 0.77% for the first 10 years and reduce water cut by 18.05%,and the final recovery will be enhanced by 1.6%.