Introduction
The complex bedding structure of shale may make its ultrasonic characteristics complicated, and make it difficult to calculate the mechanical parameters of the shale reservoir accurately. Analyzing the data of shale gas blocks, Josh et al.[1] found that the complex bedding structure of the shale led to anisotropy of the acoustic logging data. Vernik et al.[2] and Deng et al.[3] reached similar conclusion through the anisotropy of shale velocity. Horne et al.[4] used dipole acoustic logging data to judge the elastic anisotropy of layered shale, and the estimated anisotropy was consistent with the predicted value of adjacent wells. Zhang et al.[5] measured the vertical and horizontal ultrasonic velocities of two rock masses, and found obvious velocity anisotropy parallel with and perpendicular to the bedding. Yan et al.[6], Cheng et al.[7,8] studied the wave velocity changes of shale under uniaxial and triaxial compression conditions respectively, and found that the P and S wave velocities increased first and then decreased with the increase of axial load. Chen et al.[9], Xiong et al.[10] and Wu et al.[11] found through ultrasonic transmission experiments that the wave velocity decreased with the increase of the bedding angle or the decrease of the frequency, the attenuation coefficient increased with the increase of the angle or frequency, the velocity parallel with the bedding direction was positively correlated with the bedding density, while the velocity perpendicular to the bedding direction was negatively correlated with the bedding density. Schn et al.[12] established a function of shale elastic properties based on ultrasonic experiments and calculated velocity and anisotropy by this function.
In summary, domestic and foreign researchers mainly used outcrops or downhole cores to make physical models with different bedding structures, and summarized the qualitative understanding of shale acoustic responses by ultrasonic transmission experiments[13,14]. Since shale samples are difficult to prepare and a large number of shale samples are needed for and damaged in experimental study, it is impossible to carry out large-scale physical model experiments, so the research results have some limitations. In view of the above problems, taking the shale bedding structure as the research object, based on the wave theory, the ultrasonic transmission experiment process was numerically simulated to find out the ultrasonic response law of different layered models, and the gray system theory was adopted to screen the acoustic parameters sensitive to bedding structures, to establish a dynamic and mechanical shale model. The research results are of great significance for accurately predicting mechanical parameters with acoustic data.
1. Numerical simulation
1.1. Wave theory
The elasticity theory mainly studies the relationship between the applied force and deformation of an object. The wave equation is jointly established by the constitutive equation, motion equilibrium differential equation and geometric equation. For an elastic isotropic medium, the two-dimensional first-order velocity, stress elastic wave equation is:
In time, the approximate solution of the time difference equation with second-order precision is used, and in space, the approximate solution of the fourth-order difference equation is used. Using the staggered grid format, it is:
The difference format of the wave equation can be derived:
1.2. Solution of the wave equation
1.2.1. Boundary conditions
In the calculation area, the left and right boundaries are basically consistent with actual conditions, and are treated as conventional reflection boundaries, while absorption conditions are set at the upper and lower boundaries and the four corner points.
1.2.2. Initial conditions
When t≤0, the velocity and displacement are zero, i.e.
1.2.3. Source conditions
1.2.4. Convergence conditions
Analysis of error propagation and accumulation is the basis for ensuring the convergence of the difference format. Dong et al.[15] deduced in detail the stability conditions of high-order difference equations for staggered grids. When the medium is uniform and isotropic, the time precision is second order, and the space precision is fourth order, the stability condition is:
Laboratory ultrasonic testing is measured using the transmission method. However, due to the heterogeneity of shale and the uncertainty of bedding distribution, it is difficult to study the influence of the bedding structure on the ultrasonic propagation characteristics. Moreover, unsmooth contact of the probe with the core and inaccurate initial time reading manually in the transmission experiment may cause errors too. Taking the vertical section of the measured core as the model, and the shot signal of the ultrasonic probe as the source, this numerical simulation derived the first-order displacement- stress elastic wave equations based on the wave theory, and calculated the half-length staggered grid and simulated the ultrasonic transmission experiments by the Matlab program.
1.3. Verification of numerical simulation
1.3.1. Waveform comparison
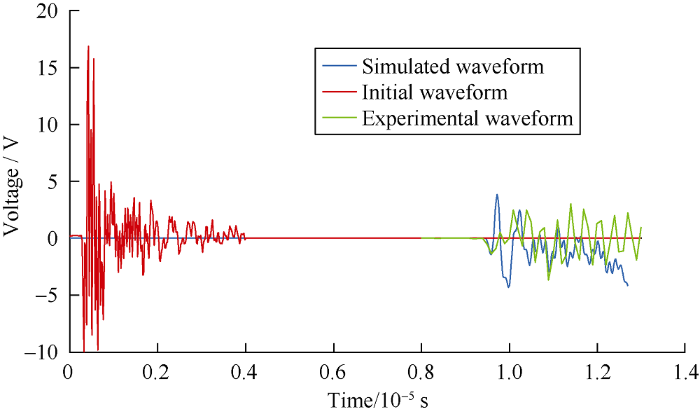
In order to make the model consistent with the ultrasonic transmission experiment, the probe frequency was set at 250 kHz. The incident wave signal was displayed as an initial waveform. When the incident signal passed through the core and reached the receiving end, the laboratory obtained the transmitted signal, which was displayed as an experimental waveform, and the result of the numerical calculation was displayed as a simulated waveform (Fig. 1). The waveform comparison show that both the simulated waveform and the experimental waveform reached the receiving end at around 0.9×10-5 s, the voltage for them were between -5 and 5 V in the similar range (Fig. 1).
Fig. 1.
Fig. 1.
Comparison of the results of standard shale ultrasonic transmission experiment and numerical simulation.
Setting the simulated waveform signal as X, and the experimental waveform signal as Y, and the correlation of the two waveforms is calculated as:
The standard deviations of X and Y are:
The covariance is:
The correlation coefficient between the simulated waveform and the experimental waveform calculated is 0.85, indicating high coincidence between them. That means that the numerical simulation method can effectively simulate the ultrasonic transmission experiment.
1.3.2. Numerical calculation
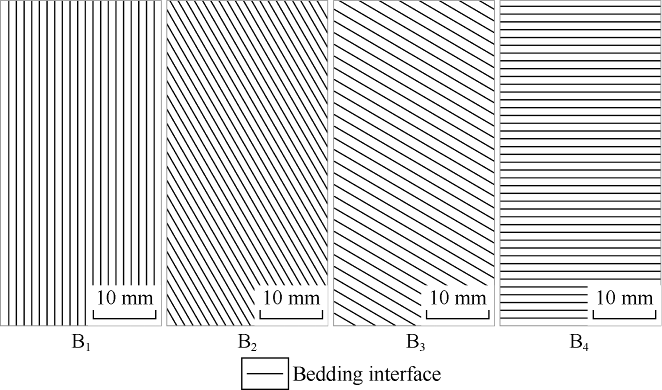
Since the bedding angle is the most significant structural feature of shale, ideal core models with different bedding angles were established based on actual cores, and numerical simulation calculations were carried out on the models. Fig. 2 shows outcrop cores from the Lower Silurian Longmaxi Formation in southeastern Chongqing, coded A1, A2, A3, and A4. The bedding angle is the angle between the bedding direction and the propagating direction of ultrasonic wave. The bedding angle of No. A1 A2, A3, and A4 are 0°, 30°, 60°, and 90° respectively (Fig. 2). In order to further verify the validity of the numerical simulation method, numerical models B1, B2, B3, B4 were established by using the cores A1, A2, A3 and A4 as templates (Fig. 3). In the models, the velocity of the ultrasonic wave in the bedding was set at 1 900 m/s, and in the skeleton at 4 200 m/s. The models have ideal bedding angles, and correspond one-by- one to the cores A1, A2, A3, and A4. On that basis, the ultrasonic transmission experiment and numerical simulation results were compared to verify the numerical simulation method.
Fig. 2.
Fig. 2.
Photograph of outcrop cores of Lower Silurian Longmaxi Formation from southeastern Chongqing (modified from reference [9]).
Fig. 3.
Fig. 3.
Numerical models of the cores from Longmaxi Formation in southeastern Chongqing (modified from reference [9]).
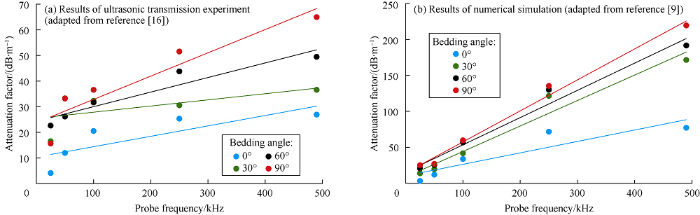
The attenuation coefficients of cores A1, A2, A3 and A4 at different probe frequencies were calculated by ultrasonic transmission experiments. The results show that at the same bedding angle, the attenuation coefficient increases as the probe frequency increases (Fig. 4a). At the same time, the attenuation coefficients of the models B1, B2, B3 and B4 at the same conditions were calculated by numerical simulation (Fig. 4b). The law obtained from the numerical simulation is basically consistent with the law from the ultrasonic transmission experiments[16], that is, at the same bedding angle, the attenuation coefficient is positively correlated with the probe frequency.
Fig. 4.
Fig. 4.
Comparison of ultrasonic attenuation characteristics from numerical simulation and experiment (4 samples).
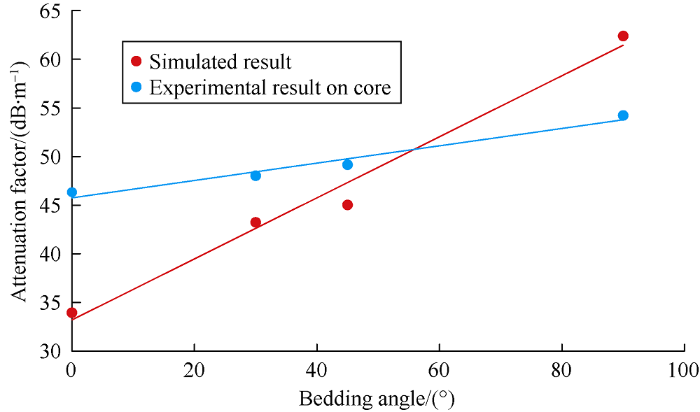
The above numerical calculations are based on ideal bedding angle models. To further verify the reliability of the above numerical simulation results, numerical image processing method was used to extract the bedding angle of real cores, and then the attenuation coefficient at different bedding angles were calculated. Fig. 5 shows the photograph of outcrop cores from the Lower Silurian Longmaxi Formation in southeastern Chongqing, coded C1, C2, C3, C4. The bedding angle of C1, C2, C3 and C4 are 0°, 30°, 45°, and 90° respectively (Fig. 5).
Fig. 5.
Fig. 5.
Photograph of the outcrop cores from the Lower Silurian Longmaxi Formation in southeastern Chongqing.
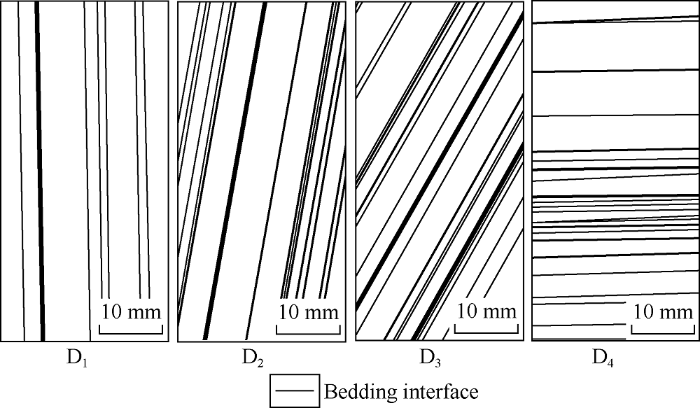
Taking cores C1, C2, C3 and C4 as research objects, edge extraction and Hough line detection were carried out on the bedding and matrix skeleton in the photographs[17], to establish four numerical simulation models, coded D1, D2, D3, D4 (Fig. 6) corresponding to C1, C2, C3, C4 in bedding angle, respectively. Since the digital image is composed of rectangular pixels, and each pixel is a small square, these small squares can be used as quadrilateral elements in finite difference calculation, so the digital image extracted for the bedding structure can be easily converted into finite difference grids by mapping the square elements. First, the coordinates of the four nodes of each unit were converted into the physical coordinates of the corresponding vector space according to the proportional relationship between the actual and pixel sizes of the image, and then the entire image could be converted into square finite difference grids. This method is called square unit mapping method. Then, according to the gray value of each pixel point, each unit was given a corresponding parameter, thereby the bedding structure characterized by the digital image was introduced to the numerical model. Finally, the Matlab algorithm was used to carry out numerical simulation calculation, and the calculation results were compared with the results of ultrasonic transmission experiments. The results show that the attenuation coefficient from the numerical simulation is positively correlated with the bedding angle, which is basically consistent with the law of the attenuation coefficient from the ultrasonic transmission experiment on cores (Fig. 7).
Fig. 6.
Fig. 6.
Extracted bedding structure of cores from the Lower Silurian Longmaxi Formation in southeastern Chongqing.
Fig. 7.
Fig. 7.
Results from experiments and numerical simulation (4 samples).
In summary, to cope with the high cost of ultrasonic transmission experiments, and errors caused by unsmooth contact between the core and the probe and human[18], the results from numerical simulation method for shale ultrasonic transmission experiments proposed in this study are in good agreement with actual ultrasonic transmission experiment results. Therefore, the numerical simulation method can be used to study the acoustic characteristics of shale bedding structure.
2. Influence of shale bedding structure on ultrasonic characteristics
2.1. Influence of bedding structure on ultrasonic characteristics
A prominent feature of shale is developed bedding structure. The parameters characterizing bedding structure mainly include bedding angle, bedding thickness and bedding density. In order to carry out numerical simulation consistent with the conditions of ultrasonic transmission experiments, the core plugs in the models were set at 50 mm high and 25 mm in diameter, the P wave velocity was 4 200 m/s and the S wave velocity 2 500 m/s in the shale skeleton, the P wave velocity was 1 900 m/s and the S wave velocity 1 100 m/s in the shale bedding, the skeleton density was 2.6 g/cm3, and the bedding density was 2.3 beddings/cm2. The incident wave from the laboratory probe was taken as the initial wave, and the direction of the ultrasonic wave kept unchanged. The cross section of the core was divided into grids (250 mm long and 125 mm wide) with the grid spacing of 0.2 mm and the time step of 20 ns. By changing the bedding model parameters, different bedding structures of shale were simulated to find out the influence of the bedding structure on ultrasonic characteristics.
2.1.1. Influence of bedding thickness on ultrasonic characteristics
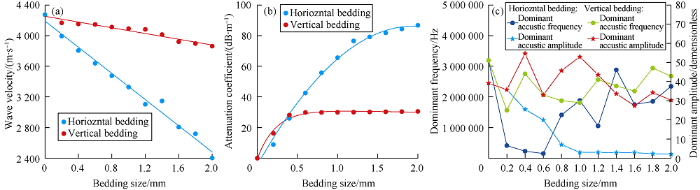
When setting the model parameter, the bedding that is straight and parallel to the layer was defined as a horizontal bedding, and the bedding that is straight and perpendicular to the layer was defined as vertical bedding. At the same the bedding angle and density, the vertical bedding thickness was set at 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0 mm respectively. The models of this group were coded E1 to E11. In another group of models, the horizontal bedding thickness was set at these thicknesses and coded F1 to F11 respectively. In the two groups of models, the ultrasonic transmitted from the bottom to the top of the core. In this study, the E2, E10 and F2 and F10 models with obvious bedding thickness and structure characteristics were selected to analyze the influence of bedding thickness on the ultrasonic characteristics, and analyze the effect of bedding thickness on ultrasonic characteristics microscopically further by wave field snapshot. The bedding thickness of E2 and E10 are 0.2 mm and 1.8 mm respectively, that of F2 and F10 are 0.2 mm and 1.8 mm respectively too. From the numerical calculations of wave velocity, with the increase of bedding thickness, the wave velocity decreases linearly both in the horizontal bedding and the vertical bedding, but that in the horizontal bedding decreases more rapidly (Fig. 8a). The calculated results of attenuation coefficient show that with the increase of bedding thickness, the attenuation coefficient increases in both horizontal bedding and vertical bedding models, the attenuation coefficient in horizontal bedding increases in a power function, while that in the vertical bedding increases in an exponential function (Fig. 8b). The calculated results of dominant ultrasonic frequency and dominant amplitude show that, with the change of bedding thickness, the dominant ultrasonic frequency in the vertical bedding and horizontal bedding, and the dominant ultrasonic amplitude in the vertical bedding change irregularly, while the dominant ultrasonic amplitude in the horizontal bedding tends to decrease on the whole as the bedding thickness increases (Fig. 8c).
Fig. 8.
Fig. 8.
Influence of bedding thickness on ultrasonic characteristics (22 models).
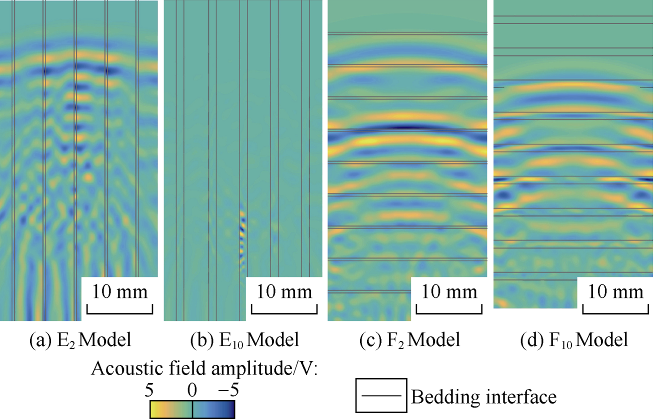
In the previous preset models, the vertical bedding thickness of E10 was larger than the vertical bedding thickness of E2, and the ultrasonic wave propagated from the bottom to the top of the core in both. The wave field snapshots show the distance that the ultrasonic signal can reach in E10 is shorter than that in E2 in the same time interval (Fig. 9a, 9b), so the ultrasonic wave velocity is lower in E10 (Fig. 8a). The horizontal bedding propagation of the ultrasonic wave in F2 and F10 follows the same law, that is, as the bedding thickness increases, the propagation distance of the ultrasonic signal in F10 is shorter in the same time interval, indicating that the ultrasonic wave velocity is smaller in F10. In Fig. 9, different acoustic field amplitudes are used to characterize the ultrasonic transmission energy. It is obvious that the color of E10 is lighter than E2, indicating that the transmitted ultrasonic energy is smaller in E10 as the vertical bedding thickness increases (Fig. 9b). Therefore, its attenuation coefficient is also larger (Fig. 8b). In the models with horizontal bedding F2 and F10, the same variation rule as E2 and E10 is revealed, that is, as the thickness of the bedding increases, the transmitted ultrasonic energy decreases (Fig. 9c, 9d), and the attenuation coefficient increases (Fig. 8b).
Fig. 9.
Fig. 9.
Wavefield snapshot of bedding thickness models.
2.1.2. Influence of bedding density on ultrasonic characteristics
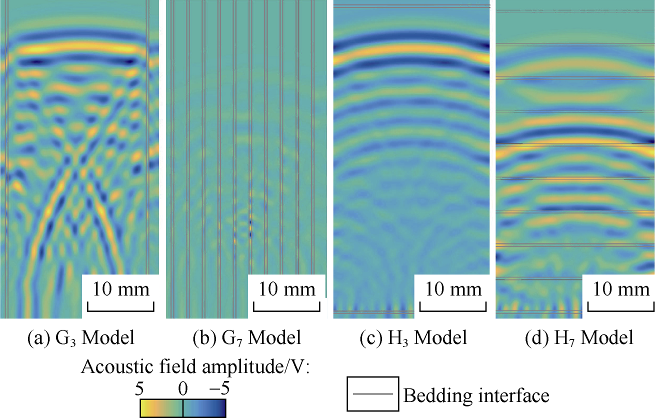
Under given bedding angle and thickness, the variation of bedding density was simulated by adjusting the number of bedding, that is, the number of bedding per unit area of the core section. With the vertical bedding thickness set at 0.4 mm, and the numbers of beddings were set at 0, 1, 2, 4, 5, 6, 10, 12, 15, 18, and 20, corresponding to the bedding density of 0, 0.08×104, 0.16×104, 0.32×104, 0.40×104, 0.48×104, 0.80×104, 0.96×104, 1.20×104, 1.44×104, and 1.60×104 beddings/m2, respectively. The models of this group were coded G1 to G11. Models of another group with horizontal beddings were coded H1 to H11, which have the bedding density same as the corresponding ones in the above group. The G3, G7 and H3 and H7 models which can better reflect the bedding density were selected to analyze the influence of the bedding density on the ultrasonic characteristics of the two groups of models, and analyze how the bedding density influences on the ultrasonic characteristics microscopically by wavefield snapshots. The bedding density of G3 and G7 are 0.16×104 beddings/m2 and 0.80×104 beddings/m2 respectively, that of H3 and H7 are 0.16×104 beddings/m2 and 0.80×104 beddings/m2 too.
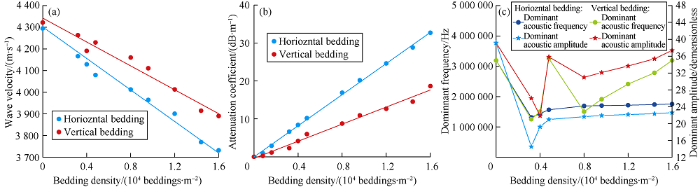
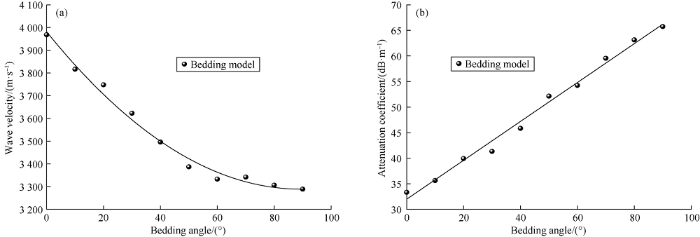
The calculation results of wave velocity show that with the increase of bedding density, the wave velocity decreases linearly both in the horizontal bedding and in vertical bedding, and that in the vertical bedding decreases less (Fig. 10a). The numerical calculation results of the attenuation coefficient show that the attenuation coefficient increases linearly with the increase of the bedding density (Fig. 10b). The calculated results of dominant ultrasonic frequency and amplitude show that the dominant ultrasonic frequency and amplitude in the vertical bedding change irregularly with the increase of the bedding density, but in the horizontal bedding, with the increase of the bedding density and when the density is less than 0.3×104 beddings/m2, the dominant frequency and amplitude decrease, and when the density is more than 0.3×104 beddings/m2, the dominant frequency and amplitude rise slowly till basically keep stable (Fig. 10c).
Fig. 10.
Fig. 10.
Influence of bedding density on ultrasonic characteristics (22 models).
The bedding density was preset in the models. Because the G7 bedding density is larger than the G3 bedding density, the H7 bedding density is larger than the H3 bedding density, the ultrasonic wave propagated from the bottom to the top of the core, and the ultrasonic wave passed through more interfaces between the bedding and the skeleton in G7 than in G3. The snapshots of the wave field show that the ultrasonic signal propagates a shorter distance in G7 than in G3 in the same time interval (Fig. 11), so the ultrasonic velocity is also smaller in G7 (Fig. 10a). The propagation of ultrasonic wave in horizontal bedding in H7 and H3 follows the same rule, that is, the propagation distance of the ultrasonic signal is shorter in H7 than in H3 in the same time interval, indicating that the ultrasonic wave velocity is also lower in H7 than in H3. In terms of attenuation, as the bedding density increases, G7 has more beddings than G3, and thus stronger heterogeneity than G3. Due to the unequal modulus between the bedding and skeleton, a certain strain phase difference was generated between the skeleton and the bedding, so internal friction was generated at the interface, and the mechanical energy was converted into thermal energy, which greatly consumed energy[19]. In Fig. 11, different acoustic field amplitudes are used to characterize the ultrasonic transmission energy. The G7 color is lighter than G3 (Fig. 11), therefore the ultrasonic transmission energy in G7 is apparently lower than that in G3, and the attenuation factor of G7 is larger than that of G3 (Fig. 10b). Similarly, H3 and H7 show the same law, that is, as the bedding density increases, the ultrasonic transmission energy in H7 is smaller, indicating that its attenuation coefficient is larger.
Fig. 11.
Fig. 11.
Wave field snapshot of bedding density models.
2.1.3. Influence of bedding angle on ultrasonic characteristics
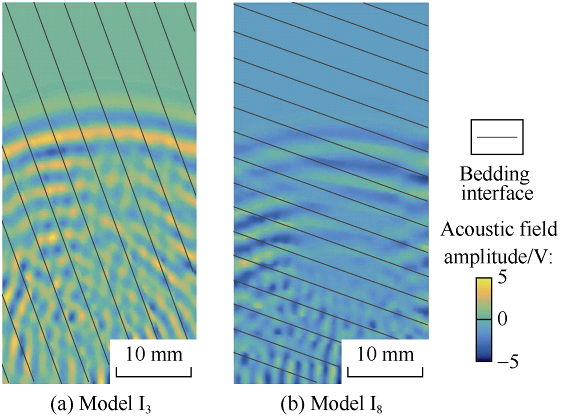
With the bedding thickness and density kept constant, the models were set at the bedding angle of 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90° and coded as I1 to I10 respectively. In this paper, I3 and I8 with obvious bedding angle features were selected to analyze the influence of bedding thickness on ultrasonic characteristics microscopically with their wave field snapshots. The bedding angle of I3 and I8 are 30° and 80° respectively.
Fig. 12.
Fig. 12.
Influence of bedding angles on ultrasonic characteristics (11 models).
The bedding angle of the model I8 preset was larger than the bedding angle of I3, the ultrasonic wave propagated from the bottom to the top of the core, and under the premise of the same bedding density, I8 has more bedding interfaces than I3. Their wave field snapshots show that the distance that the ultrasonic signal can propagate in I8 is shorter than that in I3 in the same time interval (Fig. 13a, 13b), and the wave velocity in I8 is lower (Fig. 12a). In terms of attenuation, since there are more interfaces between the skeleton and the bedding in I8 than in I3, there are more paths that hinder ultrasonic propagation in I8 than in I3. In Fig. 13, different acoustic field amplitudes are used to characterize the ultrasonic transmission energy. The color of I8 is generally lighter than that of I3, indicating that the transmitted ultrasonic energy of I8 is lower, so the attenuation coefficient in I8 is larger than in I3 (Fig. 12b).
Fig. 13.
Fig. 13.
Wave field snapshot of bedding angle models.
2.2. Statistical analysis of ultrasonic characteristics
Based on the numerical simulation results of shale, the sensitivity of acoustic parameters to the bedding structure was quantitatively analyzed by the grey system correlation method[20]. Firstly, acoustic parameters such as ultrasonic velocity and attenuation coefficient were used as reference sequences, and the structural parameters such as bedding angle, density and thickness were taken as comparison sequences:
The data was averaged dimensionless, i.e.
The correlation coefficient of the sequence is:
The correlation coefficient of the entire series is:
In the acoustic parameters, apart from the velocity that is sensitive to the bedding angle and density (with correlation value of over 0.80), the attenuation coefficient is also sensitive to the bedding thickness (with correlation value of 0.89), while the dominant amplitude and frequency are less correlated with the bedding structure (with correlation value of below 0.60) (Table 1). Therefore, in the process of utilizing the acoustic parameters to characterize the shale bedding structure in the future, in addition to the conventional sensitive factor, velocity, the attenuation coefficient can be employed jointly.
Table 1 The correlation between bedding structure and influencing factors.
| Bedding structure | Velocity | Attenuation coefficient | Dominant amplitude | Dominant frequency |
|---|---|---|---|---|
| Thickness | 0.76 | 0.89 | 0.52 | 0.58 |
| Density | 0.85 | 0.79 | 0.54 | 0.44 |
| Angle | 0.81 | 0.67 | 0.58 | - |
3. Dynamic mechanical parameters models of shale
3.1. Building of dynamic mechanical parameter models of shale
Using rock wave velocity to establish a dynamic mechanical parameter model is the method most commonly used in field development. The isotropic model and the lateral isotropic model are expressed as follows:
The isotropic mechanical parameter prediction model is:
The lateral isotropic mechanical parameter prediction model is[21]:
It is found through numerical simulation that it’s not feasible to establish the dynamic mechanical parameter model of shale only with wave velocity, and the attenuation coefficient sensitive to the anisotropic characteristics should be incorporated to achieve better results. The wave velocity and attenuation coefficient of the Longmaxi Formation shale in the Pengshui area of southeastern Chongqing measured by experiments, and the McQuaid and global optimization algorithms[22] were used to establish the dynamic mechanical parameter model considering dimension of the shale:
3.2. Verification of the models
The density of the cores from Wells ZY1 YY1 were measured by physical properties experiments, the elastic modulus and Poisson’s ratio were obtained by mechanics experiments, and the P and S wave velocities were obtained by ultrasonic transmission experiments (Table 2). Then the models proposed in this paper were verified. The experimental results in Table 2 were taken into the isotropic model established by equations (14) and (15), and into the lateral isotropic model established by equations (16) and (17) to verify the models.
Table 2 Results of core experiments.
| Well | Bedding angle/° | Bedding density/ (g·cm-3) | Vertical P-wave velocity/(m·s-1) | Vertical S-wave velocity/(m·s-1) | Elastic modulus/MPa | Radial P-wave velocity/(m·s-1) | Radial S-wave velocity/(m·s-1) |
|---|---|---|---|---|---|---|---|
| YY1 | 0 | 2.60 | 4 368 | 2 638 | 21 932 | 3 900 | 2 510 |
| 0 | 2.53 | 4 765 | 2 610 | 39 603 | 3 830 | 2 510 | |
| 15 | 2.55 | 4 433 | 2 648 | 32 784 | 3 635 | 2 300 | |
| 15 | 2.53 | 4 254 | 2 677 | 28 745 | 3 680 | 2 430 | |
| 30 | 2.59 | 4 177 | 2 621 | 28 037 | 3 970 | 2 600 | |
| 30 | 2.56 | 4 183 | 2 724 | 27 912 | 4 185 | 2 630 | |
| 60 | 2.60 | 3 974 | 2 595 | 26 199 | 4 180 | 2 620 | |
| 60 | 2.56 | 3 676 | 2 428 | 24 936 | 4 260 | 2 680 | |
| 75 | 2.55 | 3 635 | 2 266 | 24 432 | 4 430 | 2 650 | |
| 90 | 2.59 | 3 832 | 2 202 | 32 022 | 4 770 | 2 810 | |
| 90 | 2.58 | 3 896 | 2 509 | 24 849 | 4 370 | 2 640 | |
| 0 | 2.57 | 4 331 | 2 333 | 23 815 | 4 696 | 2 683 | |
| 0 | 2.57 | 4 222 | 2 470 | 22 963 | 4 500 | 2 571 | |
| 15 | 2.60 | 4 529 | 2 380 | 26 085 | 4 801 | 2 743 | |
| 15 | 2.58 | 4 386 | 2 601 | 23 826 | 4 521 | 2 583 | |
| 60 | 2.55 | 4 168 | 2 632 | 40 984 | 5 200 | 2 971 | |
| 70 | 2.53 | 4 578 | 2 616 | 26 695 | 4 689 | 2 679 | |
| 70 | 2.58 | 4 581 | 2 618 | 26 695 | 4 699 | 2 685 | |
| 75 | 2.52 | 4 435 | 2 595 | 42 524 | 5 131 | 2 932 | |
| 75 | 2.55 | 4 366 | 2 688 | 43 960 | 5 138 | 2 936 | |
| 75 | 2.54 | 4 433 | 2 648 | 43 725 | 4 829 | 2 759 | |
| 75 | 2.62 | 4 254 | 2 677 | 42 555 | 4 902 | 2 801 | |
| ZY1 | 80 | 2.60 | 4 634 | 2 729 | 26 198 | 4 788 | 2 736 |
| 80 | 2.53 | 4 410 | 2 748 | 26 022 | 4 773 | 2 727 | |
| 80 | 2.55 | 4 646 | 2 563 | 26 796 | 4 756 | 2 718 | |
| 80 | 2.53 | 4 711 | 2 773 | 27 783 | 4 431 | 2 532 | |
| 90 | 2.52 | 4 598 | 2 658 | 44 516 | 4 707 | 2 690 |
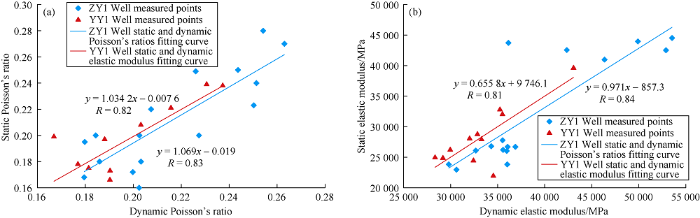
The results show that the dynamic and static mechanical parameters calculated by the models are in good agreement with experiment results. In Well ZY1, the correlation coefficient between static and dynamic Poisson’s ratios is up to 0.83, and the correlation coefficient between static and dynamic elastic moduli is 0.84. In Well YY1, the correlation coefficient between static and dynamic Poisson’s ratios is 0.82, and the correlation coefficient between static and dynamic elastic moduli is 0.81 (Fig. 14). The simulation effect of the new model proposed in this paper is better than the commonly used isotropic model and lateral isotropic model. Here the isotropic model refers to the medium with the same physical properties in different directions, and is a homogeneous model; the lateral isotropic model refers to the model with the same elasticity in any direction perpendicular to the axis, and is a heterogeneous model. The isotropic model only targets isotropic rocks, and does not consider the bedding development of shale. The lateral isotropic model regards shale as a laterally isotropic medium with structure too ideal. The model proposed in this paper is based on wave velocity and attenuation, the most sensitive parameters to shale bedding structure, and established by the general global optimization algorithm. The models can better reflect the influence of shale bedding structure, the dynamic moduli calculated by the models are generally larger than the corresponding static moduli, and the dynamic Poisson’s ratio to the static Poisson’s ratio is basically 1 to 1. They are basically consistent with the relationship obtained by Kuhlman et al.[23].
Fig. 14.
Fig. 14.
Comparison and verification of dynamic mechanical parameter models (R—correlation coefficient).
3.3. Field verification of models
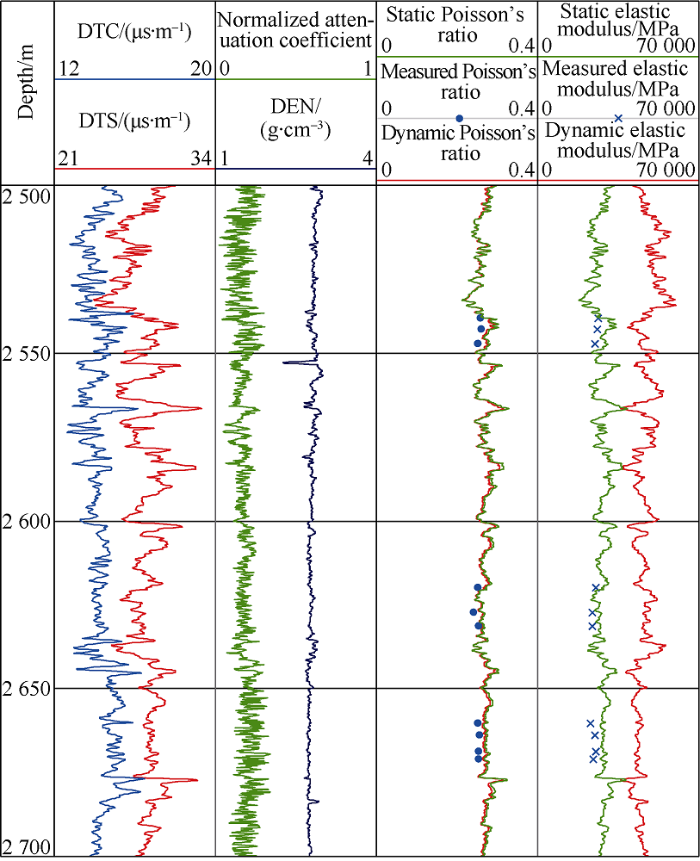
The logging data of Well ZY2 in southeastern Chongqing was collected to carry out the inversion of the dynamic parameters of the rock mechanics, and the results of the static mechanical parameters were obtained by core experiments. Fig. 15 shows that the dynamic elastic modulus is generally larger than the static elastic modulus, and the dynamic Poisson’s ratio is very close to the static Poisson’s ratio, which is basically 1 to 1, in the inverted depth range. These are consistent with the model results mentioned above. Meanwhile, rock mechanics experiments were carried out on 10 cores from different depths of the Longmaxi Formation in Well ZY2, and inversion data of field logging data was verified by the experimental results.
Fig. 15.
Fig. 15.
Predicted results of mechanical parameters of the Lower Silurian Longmaxi Formation in Well ZY2 (DTC—P wave time difference, DTS—S wave time difference, DEN—rock density).
Table 3 shows that the inverted mechanical parameters at 10 different depths are basically consistent with the experimental results of cores. Through calculation, the relative error of the Poisson’s ratio is less than 10%, and 6.94% on average; the relative error of the elastic modulus is 21.25% at maximum and 15.30% on average. Clearly, the mechanical profile inverted by the logging data can accurately reflect the real rock mechanical parameters. The dynamic mechanical parameter models established in this paper are suitable for the shale with developed bedding structure.
Table 3 Error analysis of mechanical parameters.
| Depth/ m | Experimental results | Inversion results from the model | ||||
|---|---|---|---|---|---|---|
| Poisson’s ratio | Elastic modulus/ MPa | Relative error/% | Poisson’s ratio | Elastic modulus/ MPa | Relative error/% | |
| 2 539.74 | 0.26 | 26 356 | 8.86 | 0.28 | 30 542 | 15.88 |
| 2 543.08 | 0.26 | 26 134 | 7.04 | 0.27 | 29 795 | 14.01 |
| 2 547.20 | 0.25 | 25 135 | 9.52 | 0.27 | 29 588 | 17.72 |
| 2 619.89 | 0.25 | 25 541 | 6.63 | 0.26 | 28 145 | 10.19 |
| 2 627.20 | 0.24 | 23 839 | 8.48 | 0.26 | 26 797 | 12.40 |
| 2 631.47 | 0.25 | 24 057 | 4.80 | 0.26 | 27 540 | 14.48 |
| 2 660.43 | 0.25 | 23 036 | 6.58 | 0.26 | 27 933 | 21.25 |
| 2 663.93 | 0.26 | 25 180 | 6.90 | 0.27 | 29 221 | 16.04 |
| 2 668.81 | 0.25 | 25 289 | 7.17 | 0.27 | 28 609 | 13.12 |
| 2 671.10 | 0.25 | 24 202 | 5.26 | 0.26 | 27 690 | 14.41 |
4. Conclusions
Based on the wave theory, a numerical simulation method of ultrasonic transmission experiment on shale was worked out by using the staggered grid finite difference method. The correlation coefficient between the simulated waveform and the experimental waveform is greater than 80%, which indicates that the numerical simulation method can effectively simulate the ultrasonic transmission experiment.
In the ultrasonic parameters, the acoustic velocity is a conventional sensitivity factor used to characterize shale bedding structure, but the normalized attenuation coefficient is needed to comprehensively describe the shale bedding to make the result more accurate.
Based on the wave velocity and attenuation coefficient of ultrasonic transmission experiments, the mechanical parameter models of the Lower Silurian Longmaxi Formation in southeastern Chongqing were established. The correlation between the dynamic and static parameters calculated by these models is better than the traditional model. The predicted values of the rock mechanics profile obtained from inverting logging data and the model are in good agreement with the experimental results.
Nomenclature
A, B—discrete values of velocities u and ν, dimensionless;
D, E, F—discrete values of stresses τxx, τxz, τzz, dimensionless;
E1, E2—elastic moduli parallel and perpendicular to the isotropic plane, MPa;
i, j, k—time and space grids, dimensionless;
G2—shear modulus in the isotropic plane, MPa;
p, q—parameters, dimensionless;
R1—Acoustic displacement, m;
U, V—x and z velocities, m/s;
τxx, τxz, τzz—stress components, MPa;
Yi, Xi—reference sequence and comparison sequence, dimensionless;
ξi(k)—correlation coefficient of Xi(k) and Yi(k) at point k, dimensionless;
ri—correlation degree of Xi(k) and Yi(k), dimensionless;
ν1, ν2—Poisson’s ratios parallel and perpendicular to the isotropic plane, dimensionless;
Vp, Vs—P and S wave velocities, m/s;
λ, μ—Lame constant, dimensionless;
ρj—medium density, g/cm3;
ρ—core density, g/cm3;
χ—normalized attenuation coefficient, dimensionless.
Reference
Laboratory characterization of shale properties
DOI:10.1016/j.petrol.2012.01.023
URL
[Cited within: 1]

78 We introduce an improved workflow for systematic gas shale characterization. 78 A suite of shales from a number of sedimentary basins around the world. 78 Petrophysics using XRD, XRF, CEC, SSA often correlate with geomechanical properties. 78 Permeability can be determined using Mercury Injection Capillary Pressure (MICP). 78 SEM and X-ray CT imaging provide additional correlating parameters.
Ultrasonic and anisotropy of hydrocarbon source rocks
DOI:10.1190/1.1443286 URL [Cited within: 1]
Analysis of the velocity anisotropy and its affection factors in shale and mudstone
DOI:10.1002/cjg2.575
URL
[Cited within: 1]

The velocity anisotropy is examined in laminated shale and mudstone under the laboratory ultrasonic frequency. The variation patterns of wave velocity in different directions as a function of confining pressure are also presented for dry and oil-saturated situations. Using the X-ray diffraction technique and electron microprobe imaging, we make analysis and conclude that the clay minerals and microcracks are the intrinsic factors that result in such strong anisotropy in rock samples. With the increasing confining pressure, microcracks are gradually closed, which low the anisotropy. Pore fluid increases the pore rigidity thus decreases the tendency of anisotropy change with confining pressure.
Elastic anisotropy in the Haynesville Shale from dipole sonic data
Elastic constants of foliated rock by use of P-wave probes
Velocity characteristic of P-wave and S-wave for shale reservoir under tri-axial compression experiments
In view of the characteristics of developed bedding and strong anisotropy, a series of ultrasonic velocity experiments were conducted under the tri-axial compression with drilling cores. The variation characteristics of P-wave and S-wave were obtained at different dip angle and axial load. The experimental results show that: when the bedding dip angle increases, the compressive strength and residual strength appear to be U type change tendency with gradually increasing modulus of elasticity while the Poisson′ s ratio increases first and then drops; the initial P-wave and S-wave velocities of shale increase with the increase of the bedding dip angle; with the effect of axial load on the internal structure of shale, the velocities of P-wave and S-wave increase first and then decrease; the velocities of P-wave and S-wave increase when the shale hydration occurs; the correlation coefficient of dynamic elastic modulus to static elastic modulus is close to the ratio of dynamic Poisson′ s ratio to static Poisson′ s ratio, the correlation coefficient are well related; under confining pressure, there are less differences within the anisotropy coefficients of elastic modulus and the Poisson′ s ratio of the shale. The experimental results in the article have guiding significance to the understanding and interpretation of mechanical properties, ultrasonic characteristics and acoustic logging.
Effect of bedding angle on shale tri-axial stress, testing and velocity of P-wave and S-wave
In view of the characteristics of shale reservoir with significant bedding,tri-axial compression experiments and ultrasonic testing has been carried out in consideration of the bedding angle,the influence of failure pattern,strength,elastic modulus,Poisson's ratio and ultrasonic velocity at the bedding angle were obtained,the relationship between axial stress and velocity of longitudinal wave were defined,the relative coefficient between the dynamic and static elastic modulus and Poisson's ratio of shale reservoir is established,the coefficient of variation and anisotropy of mechanical parameters and ultrasonic velocity were analyzed.Results show that the mechanical parameters and velocity of longitudinal wave varied linearly by the bedding angle,the positive correlation between axial stress and velocity of longitudinal,the correlation coefficient of static elastic parameters and Poisson's ratio was 1.39and1.18,the mean value of variation coefficient of mechanical parameters and anisotropy coefficient was larger than ultrasonic velocity.The results can offer basic parameters for shale log interpretation,well drilling and hydraulic fracture.
Numerical simulation of ultrasonic wave transmission experiments in rocks of shale gas reservoirs
DOI:10.1063/1.4974749
URL
[Cited within: 1]

Shale gas reservoirs have risen in importance in China's new power source exploration and development program. The investigation of the propagation of ultrasonic waves in shale forms the basis for the full waveform application of acoustic logging data to the exploration of shale gas. Using acoustic wave theory, initial conditions, vibration source conditions, and stability conditions are developed in combination with experimental background of ultrasonic wave transmission. With improved boundary conditions, we performed numerical simulations of the ultrasound transmission experiments in shale using the high-order staggered-grid finite difference method (second-order in the time domain and fourth-order in the space domain). With programs developed within MatLab, the results obtained from numerical simulations agree well with experimental results based on physical models. In addition, using snapshots of the wave field that give a microscopic perspective, the propagation laws for ultrasonic waves can be analyzed. Using this method, human error is avoided, transmission experiments costs can be reduced and efficiency improved. This method extends the scope of experimental investigations regarding the transmission of ultrasonic waves in a shale gas reservoir with increasing stratification, and thus has great theoretical value and practical significance.
Experimental study on acoustic penetration through the Longmaxi Formation shale rock in south region of Sichuan Basin
To acquire the law of acoustic propagation property of the Longmaxi formation shale,we first collected the rock from shale outcrops of the Lower Silurian Longmaxi formation shale in the south region of Sichuan Basin,cores were drilled from different bedding angle(ten bedding angles),meanwhile the P-wave velocity and S-wave velocity of Longmaxi formation shale were studied using acoustic penetration experiments in the laboratory,and the dynamic elasticity parameters of shale rock were computed. The result shows that there is linear relation between P-wave velocity and S-wave velocity of the Longmaxi formation shale in the south region of Sichuan Basin. The average values of the Vp /Vs ratio and P-wave velocity of shale rock decreased with increasing in the bedding angle. There exists exponential relation between dynamic modulus,shear modulus and volumetric modulus and P-wave velocity or S-wave velocity,whereas the Poisson ratio values were liner correlated with P-wave velocity. With the increase of the bedding angle or the decrease of the frequency,the wave velocity decreases,and there is positive relationship between acoustic velocity and frequency. While the attenuation coefficient increases with the increase of the bedding angle or the increase of the frequency,and which were weakly correlated with frequency.
Acoustic characteristics of shale in the Longmaxi Formation in southeastern Sichuan Basin
Elastic wave anisotropy and shale distribution
Quantitative evaluation of rock brittleness and fracability based on elastic-wave velocity variation around borehole
DOI:10.1016/S1876-3804(16)30053-2
URL
[Cited within: 1]

Brittleness and fracability are two important rock properties in hydraulic fracturing of unconventional reservoirs. Based on the variation of compressional and shear velocity around borehole using acoustic measurement, an effective technique is developed to estimate these parameters to guide reservoir-fracturing. During drilling, when the rock is broken, a significant amount of drilling induced cracks will occur in the formation around the borehole, reducing elastic wave velocity around borehole and causing the wave velocity variation away from borehole. The radial variation of compressional and shear velocities of formation rocks surrounding a borehole were respectively obtained from P-wave travel time tomography and dipole shear-wave dispersion inversion. By integrating the two variation profiles along the radial direction, the brittleness-fracability index is obtained to estimate the brittleness and fracability of formation rocks. The index shows fairly good consistency and correlation with rock brittleness and fracability, which demonstrates the practicability and effectiveness of the proposed approach. Well log data analysis examples are presented to demonstrate the effectiveness of our technique.
Hydraulic fracture propagation geometry and acoustic emission interpretation: A case study of Silurian Longmaxi Formation shale in Sichuan Basin, SW China
A staggered- grid high-order difference method of one-order elastic wave equation
DOI:10.1016/S0009-2541(99)00189-8
URL
[Cited within: 1]

All methods of seismic wave-field simulation are trying to improve their computational accuracy and efficiency. After transforming the odd higher-order time derivatives of velocity (stress) to spatial derivatives of stress (velocity) in the high-order finite difference method, we can use any order of the temporal and spatial difference accuracy and staggered-grid technique for numerical calculation of the one-order elastic wave equations expressed with velocity and stress. The snapshots and simulated results of an actual model show that this method is more accurate and can decrease the grid dispersion in conventional difference method. Meanwhile, bigger grid space can be used in order to raise the computational efficiency.
An experimental study of ultrasonic penetration through bedding shale reservoirs
DOI:10.3787/j.issn.1000-0976.2013.08.025
URL
[Cited within: 1]

The acoustic response of bedding hard brittle shales is the foundation of well logging data interpretation during the shale gas development process.To better understand the ultrasonic penetration through bedding shale reservoirs,we first collected the shale outcrops from the Lower Silurian Longmaxi Shale in southeast Chongqing,and transversely isotropic large rock samples were preliminarily screened with the velocity test method to acquiring comprehensive knowledge on the propagation characteristics of the ultrasonic wave of bedding shale reservoirs.On this basis,cores were drilled from different bedding direction,meanwhile multi-frequency ultrasonic transmission,experiments were performed in the laboratory,thereby to get the law of acoustic wave propagation in different bedding directions.The following findings were obtained.a.Rock samples used in the experiments are mainly composed of black shale,gray and black shale,dark gray shale and silty mudstone,the porosity of which ranges from 1.5%to 2.5%,and the permeability of which is mostly less than 1mD.b.With the increase of the bedding angle within the range of 0 -90 ,the wave velocity decreases obviously while the attenuation coefficient increases.c.There is a good negative correlation between the wave velocity and porosity.Attenuation coefficient increases with the increase of porosity and its increasing degree becomes greater with the increase of the bedding angle.d.The wave velocity and the frequency both increase in a logarithm tendency,the dispersion phenomenon is obvious,and the attenuation coefficient increases with the increase of frequency.The above experimental results about the correlation between rock acoustic properties and bedding formation of shales provide a reliable experimental basis,based on which an accurate formation rock strength profile and wellbore stability analysis can be established in the process of shale gas development.
Extracting straight lines from building image based on edge orientation image
DOI:10.3788/AOS20103010.2904
URL
[Cited within: 1]

Detecting lines in a digital image is a crucial step in many applications,such as visual navigation,feature recognition and remote sensing image processing,In this paper,an algorithm which is based on edge orientation image is proposed for extracting straight lines from comples building image.Firstly,edges are detected based on Canny detector.Secondly,an edge direction coding strategy is proposed by detecting the local line in 9 9 window.Thirdly,edges are split into a series of straight lines,curves and points,and a new secondary image the edge orientation image is generated.Finally,the straight lines are extracted from the edge orientation image by analyzing the direction distribution,and using the straightness errors evaluation strategy and the sparse line fitting algorithm.Experiment results show that the proposed algorithm is better than hough transform and phase grouping algorithm.It can detect lines correctly in complex building images with high accuracy rate,low false and low missing rate and good robustness.
Elastic parameters of rocks
Numerical simulation of the fractured model acoustic attenuation coefficient
Anisotropic property of mechanical parameters of shales
DOI:10.3787/j.issn.1000-0976.2012.12.013
URL
[Cited within: 1]

In shale gas development,an obvious anisotropic property is demonstrated from the bedding of shale reservoirs.Thus,such related studies are of great significance to subsequent drilling and reservoir stimulation.First,assuming shale rocks as transverse isotropic media,we studied the coordinate transformation of transverse isotropic stress-strain relation,on this basis,derived the relationship between directional elastic modulus,Poisson ratio,and elastic constants along vertical and parallel bedding direction respectively.Then,by means of ultrasonic testing and uniaxial compression experiment,we measured compression strength,static and dynamic elastic modulus and Poisson ratio to study the impact of shale bedding on the mechanic parameters.From the experiments and theoretical calculation,the following conclusions are drawn.(1) It is relatively right from the perspective of mechanics to regard the bedding shale rocks as transverse isotropic media.(2) The elastic modulus and Poisson ratio of vertical bedding direction are smaller than those of parallel bedding direction.(3) The anisotropic property of dynamic elastic parameters is stronger than that of static elastic parameters.(4) There is regular change of elastic modulus and Poisson ratio along with bedding dip of shale rocks.(6) The elastic constants of vertical and parallel bedding directions can be used to determine the elastic modulus and Poisson ratio of any direction.
Global optimization algorithm and its application
Micro- fracture stress tests, an elastic strain recovery, and differential strain analysis assist in Bakken shale horizontal drilling program