Introduction
Drilling fluid pulse signal telemetry system is used to upload information in downhole control engineering[1]. Compared with microwave, vibration wave[2-3] and other new technologies, drilling fluid pulse is the dominant downhole data transmission technology. NOV BlackStar II MWD tool is equipped with electromagnetic (EM) and drilling fluid pulse modes to complement and back up each other[4]. The high- frequency magnetic coupling wired drill pipe (InforPipe) developed by CNPC Engineering Technology R&D Company Limited also use drilling fluid pulse as a backup information channel.
Drilling fluid pulse is affected by drilling fluid pump, air chamber, surface piping, pressure transducer location, drill string size, well depth, drilling fluid properties and other factors during transmission[5]. The main noise sources include drilling noise, drill string motion noise within the borehole and drilling fluid pump noise[6]. Signal detection and decoding techniques are critical to successful application of drilling fluid pulse technology[7].
Early matched filter algorithm[8] can eliminate noise of drilling fluid pulse. Because the drilling fluid pulse signal and drilling fluid pump noise overlap in frequency domain, the standard filter algorithm is not competent for the job anymore, so the self-adaptive filter algorithm is born at the right moment. For example, the use of two-stage filter algorithm, obtaining the direct current (DC) component with low-pass filter and eliminate the noises out of the band with bandpass filter[9]. Using the average filtering algorithm to eliminate the DC component and realize the two-stage filter algorithm[10]. Using the least mean square (LMS) evaluation criterion to establish an self-adaptive finite impulse response (FIR) filter[8]. The pump noise is the main noise source, it can also be eliminated by using two sets of standpipe pressure sensors[11]. The setting of filter parameters and threshold affect the de-noising effect, and the threshold size of threshold signal identification algorithm affects the decoding success rate. The ground system can detect and decode drilling fluid pulse automatically under normal conditions, but its parameters or threshold needs to be adjusted manually under special circumstances such as heavier drilling fluid density and gas cut[12], which would lead to longer time and higher difficulty in operation.
Fourier filtering is difficult to reveal the characteristics of unsteady signals. Wavelet transform can show the characteristics of different scales of signals and extract useful information from noise signals[13]. Discrete wavelet transform (DWT) can improve signal-to-noise ratio (SNR) and reduce error rate[14]. Continuous wavelet transform (CWT) can also be used to detect unsteady continuous drilling fluid pulse signals[15].
In this work, in order to realize automatic de-noising and recognition of drilling fluid pulse signal, the decoding process was divided into two stages, de-noising and recognition, by analyzing the properties of drilling fluid pulse signals. A de-noising algorithm based on wavelet analysis and a recognition algorithm by analyzing the properties of the de- noised signals using general modulation and coding method were designed separately, and parameters of these two-stage algorithm were tuned with a large capacity samples. Finally, the channel coding method using automatic threshold adjustment was applied to improve the decoding success rate.
1. Features of drilling fluid pulse signal
Drilling fluid pulse telemetry system uses modulated drilling fluid pressure pulse signal to transmit information. The object of this study is the commonly used pulse position modulation (PPM) signal which has a wider frame-synchronization pulse encoded at the beginning of each signal to distinguish each instruction. The width of frame-synchronization pulse is three times the width of the instruction pulse and is 6 timeslots. There is more than one protection timeslot between pulses. These protection timeslots are used to charge the energy storage capacitor of the pulse generator and provide pulse recovery time, which can eliminate interference between signals. This modulation coding mode is typical.
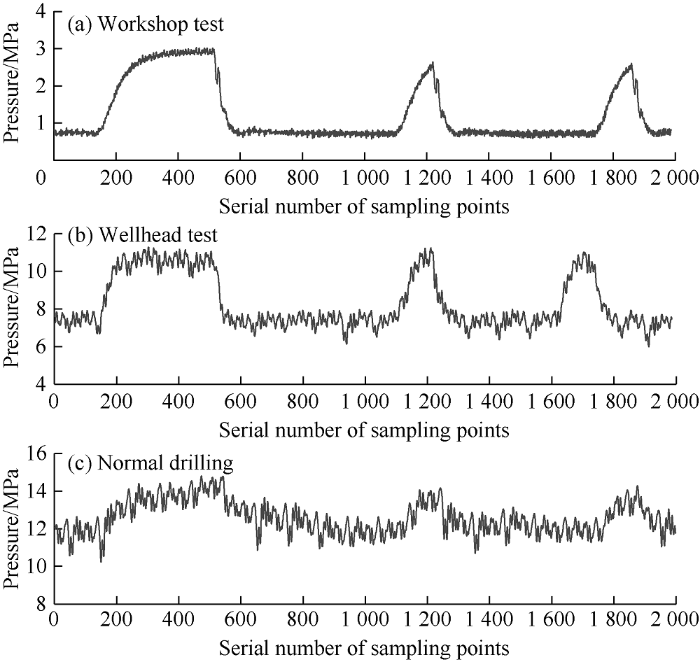
Fig. 1a shows the waveform of the pressure signal generated by the positive pulse generator during workshop test. This waveform whose driving signal is square wave includes a wider frame-synchronization pulse and subsequent two instruction pulses. The sampling rate of the standpipe pressure signal was 256 S/s. Because of the acceleration and deceleration time of the main valve head movement of the pulse generator and attenuation of the drilling fluid channel, the signal rising time increases, but rich high-frequency components are still retained. The 1-20 Hz noise generated by drilling pump is the main source of noise[11]. Fig. 1b shows the waveform acquired from the field wellhead test and Fig. 1c shows the waveform for normal operation. We can see that SNR decreases and high-frequency effective components reduce.
Fig. 1.
Fig. 1.
Features of drilling fluid pulse signals.
2. Signal de-noising algorithm
2.1. Wavelet forced de-noising
Drilling fluid pulse signal is a typical unsteady signal. Wavelet analysis which directly uses dual channel filter banks to process signals, has better de-noising effect. The Mallat algorithm of one-dimensional DWT contains two parts: decomposition and reconstruction[16]. Its decomposition algorithm is as follows:
Its reconstruction algorithm is as follows:
The effect of wavelet de-noising is related to the selection of wavelet basis functions, the level of decomposition layers and threshold processing method. In this study, the wavelet forced de-noising algorithm was used, in which high-frequency coefficients of decomposition structure were all set to zero before the wavelet reconstruction was completed.
2.2. Baseline drift rectification
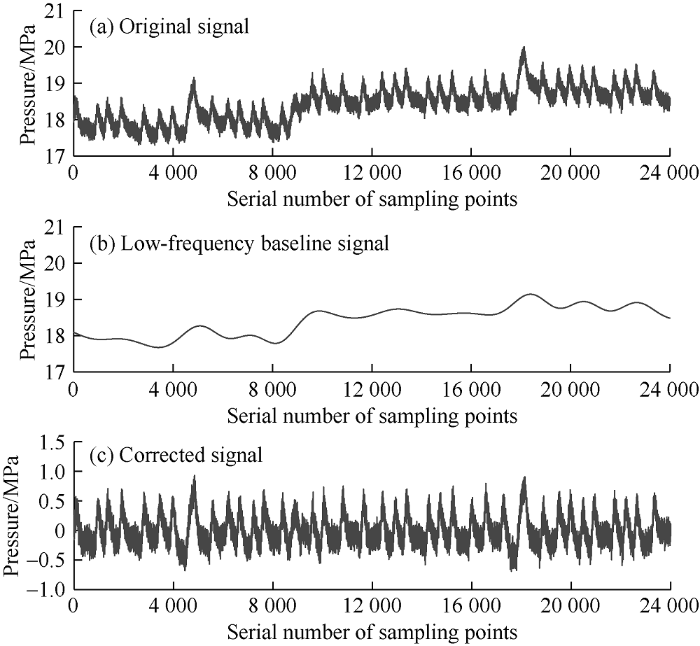
Baseline drift rectification can be achieved using wavelet analysis[17]. Fig. 2a is a drilling fluid pulse signal with baseline drift. In order to obtain low-frequency baseline signal including baseline drift, wavelet forced de-noising was used to process original signals. The processing is as follows: (1) The low-frequency baseline signal waveform (Fig. 2b) was reconstructed after removing high-frequency components with tuned parameters (wavelet basis function: discrete Meyer, decomposition level: 10), (2) the original signal was subtracted by baseline signal to get the corrected waveform (Fig. 2c). It can be seen from the figure that the low-frequency effective component of wider frame-synchronization pulse is also lost while baseline drift component is eliminated. The longer the length of the acquired signal, the greater the influence of baseline drift on decoding effect is.
Fig. 2.
Fig. 2.
Baseline drift rectification.
2.3. Two-stage de-noising processing of frame-synchronization signal and instruction signal
Since the width of frame-synchronization pulse is three times that of the instruction pulse, these two different pulses have different scaling characteristics in time domain, which can be used to segment instruction frame signal. A wavelet de-noising algorithm for two-stage processing was designed thereby: (1) The first stage de-nosing processing was designed according to the width of frame-synchronization pulse, and shorter instruction pulse sequences were achieved from dividing whole pulse sequence. (2) The second stage de-nosing processing which completes signal recognition at the same time was designed according to the width of instruction pulse. This two-stage processing de-noising algorithm can reduce the influence of baseline drift by shortening the processing length of instruction pulse sequence, determine the range of automatic peak detection threshold in signal recognition, and improve the decoding success rate.
When the original data of 2 times signal length is acquired, decoding calculation begins in order to avoid missing signals and reduce the number of time-consuming decoding calculations in the process of continuous signal acquisition.
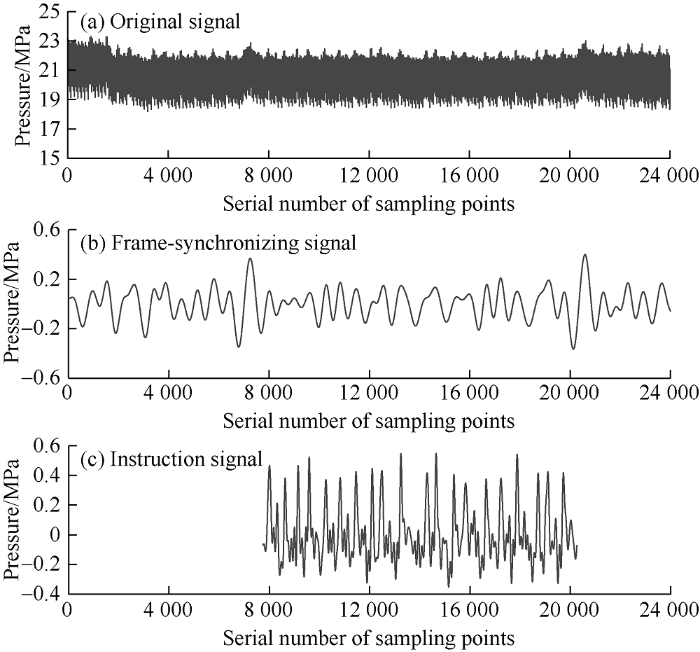
(1) The data acquired by sampling 2 times signal length was processed with wavelet de-noising algorithm in order to obtain the information of frame-synchronization pulse. The original signal shown in Fig. 3a, which contains 2 frame- synchronization pulses, that is, at least one complete signal, was processed with baseline drift rectification. After that, the de-noised frame-synchronization signal (Fig. 3b) was obtained by wavelet forced de-noising algorithm with tuned parameters (wavelet basis function: discrete Meyer, decomposition level: 8). It can be seen from the figure that the characteristics of wider frame-synchronization pulse are enhanced by proper parameters selection.
Fig. 3.
Fig. 3.
Two-stage de-noising processing of frame-synchronization signal and instruction signal.
(2) The signal between two frame-synchronization pulses was selected again to be processed with the baseline drift rectification. The shorter signals not only have smaller baseline drift but also a uniform amplitude of instruction signal variations. The de-noised instruction signals (Fig. 3c) were obtained by wavelet forced de-noising algorithm with tuned parameters (wavelet basis function: discrete Meyer, decomposition level: 6). The characteristics of instruction pulse are more obvious.
2.4. Signal de-noising process
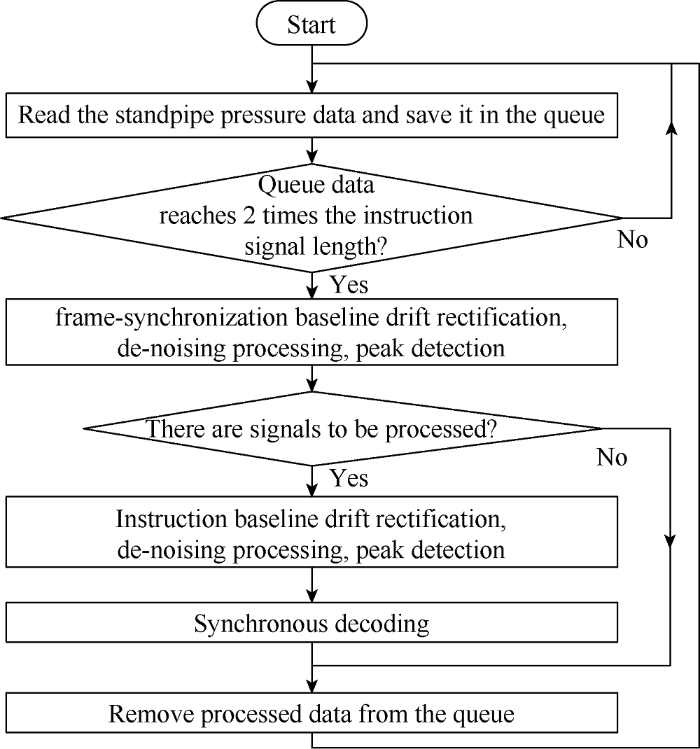
Fig. 4 is the basic process of signal de-noising. A data queue was used to save pressure values acquired from standpipe pressure sensor, and frame-synchronization and instruction signal two-stage de-noising were carried out when the acquired data reached twice the signal length. The parameters list of the signal de-noising algorithm is shown in Table 1.
Fig. 4.
Fig. 4.
Signal de-noising process.
Table 1 Signal de-noising algorithm parameters.
| Number of stages | Parameters | Number of stages | Parameters |
|---|---|---|---|
| Frame- synchro- nization | Wavelet basis function | Instruction | Wavelet basis function |
| Level of baseline drift rectification | Level of baseline drift rectification | ||
| Level of decompo- sition layers | Level of decompo- sition layers |
3. Signal recognition algorithm
3.1. Peak detection
As can be seen from Fig. 2c, even after baseline drift rectification, the bottom of each pulse is not at the same height. This means that the peak detection algorithm based on the signal absolute value as threshold value will waste valuable pulse change degree. In addition, for frame-synchronization pulse and instruction pulse, there are different signal variations between rising-edge and falling-edge. The peak of the signal after de-noising can be detected by calculating the changes of rising-edge and falling-edge of the pulse peaks.
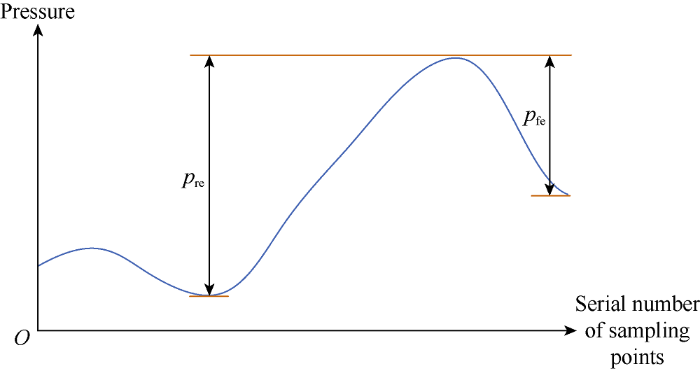
The rising-edge protruding degree (pre) and the falling-edge protruding degree (pfe) are defined respectively (Fig. 5). pre is defined as the height difference between the peak and the nearest valley to the left. If the left side is the signal edge and monotonously drops, then it is the height difference between the peak and the left edge. pfe is defined as the height difference between the peak and the nearest valley to the right. If the right side is the signal edge and monotonously drops, it is the height difference between the peak and the right edge.
Fig. 5.
Fig. 5.
Definition of protruding-degree.
In order to recognize signal automatically, the relative rising-edge protruding degree (pRre) and the relative falling- edge protruding degree (pRfe) are defined as:
The protruding degree range (prange) in formula can be simply defined as the maximum value of the de-noising signal. Only qualified pulse peaks are retained in the detection process.
Pulse peak detection can be executed based on rising-edge or falling-edge or both of them after defining the thresholds of the relative rising-edge and falling-edge protruding-degree.
3.2. Synchronous decoding
There is a strict temporal relationship between frame-syn-chronization pulse and subsequent instruction pulse. Theoretically, the frame-synchronization pulse can be used for bit-synchronization decoding simultaneously. After de-noising the signal shown in Fig. 2c with different wavelet bases, it is found that the positions of signal peaks are different for different basis functions. The deviation of frame-synchronization pulse peak position will cause inaccurate bit-synchronization. Moreover, the deviation and drift between the clock that generates the driving electrical signal and the one that samples standpipe pressure can also lead to inaccurate bit-synchronization.
In this study, instruction pulse was used as bit-synchronization pulse to improve the decoding success rate. Because the instruction pulse has similar width and signal characteristics, the position of the peak of the signal after de-noising keeps synchronization, the position of the peak of each instruction pulse can be accurately determined. In the decoding process of the subsequent instruction pulse, only the previous instruction pulse is used as the bit-synchronization pulse in turn, so that when the instruction is long, the decoding success rate will not reduce because of the error accumulation of the timeslot.
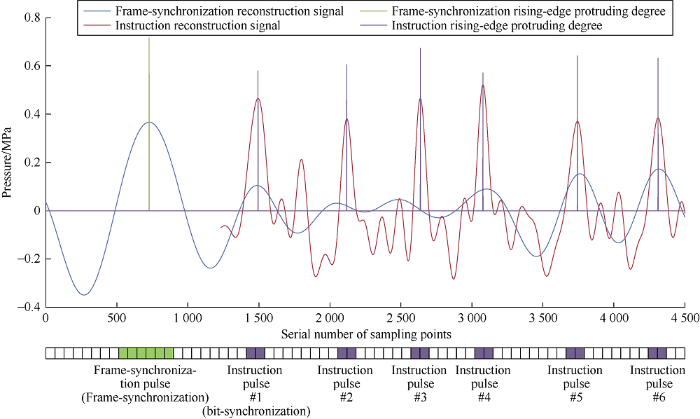
Fig. 6 shows the details of waveform after two-stage de- noising for frame-synchronization and instruction signals, including reconstruction signal of de-noised frame-synchronization and instruction signals and peak detection results satisfying the threshold of relative rising-edge protruding degree (frame-synchronization: only 70% of relative rising- edge protruding degree was used, instruction: only 50% of relative rising-edge protruding-degree was used). The peak detection value is the absolute value of the rising-edge protruding degree. The range is determined according to the maximum value of the complete instruction pulse sequence. The position of the first instruction pulse timeslot can be determined by frame-synchronization pulse. The timeslot position diagram at the bottom indicates the position of each pulse.
Fig. 6.
Fig. 6.
Synchronous decoding waveform.
3.3. Signal recognition process
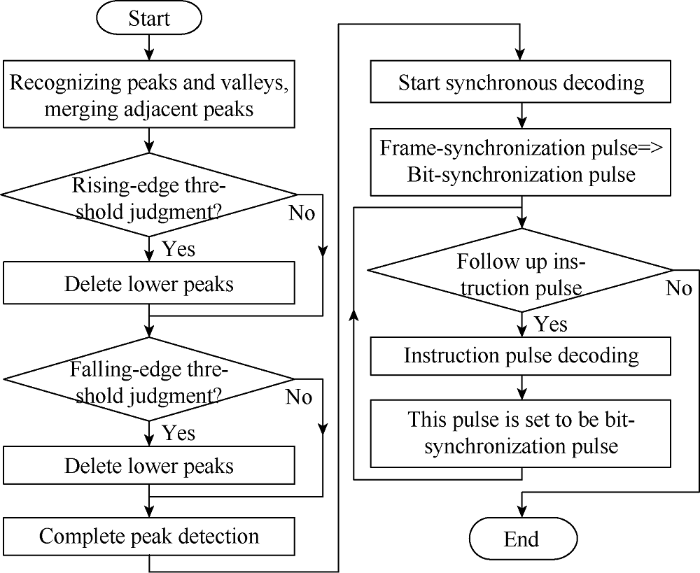
The basic process of signal recognition is shown in Fig. 7 and the parameters list of the signal recognition algorithm is shown in Table 2. For automatic peak detection, especially for automatic peak detection of de-noised frame-synchronization signal, when there is no valid drilling fluid pulse signal, prange is small, which may lead to wrong identification result of frame-synchronization pulse. In this case, it is necessary to distinguish whether the detected peak is noise by combining number and interval of frame-synchronization pulses.
Fig. 7.
Fig. 7.
Signal recognition process.
Table 2 Parameters for signal recognition algorithm.
| Stage | Parameter | Stage | Parameter |
|---|---|---|---|
| Frame- synchro- nization | Relative rising-edge protruding degree threshold | Instruc- tion | Relative rising-edge protruding degree threshold |
| Relative falling-edge protruding degree threshold | Relative falling-edge protruding degree threshold |
4. Algorithm parameter tuning
4.1. Sample preparation
Large capacity samples are used not only for parameter tuning, but also determine the applicability of the algorithm parameters after tuning. Even for the same well, because of the different operation conditions such as well depth and drilling fluid density, the influence of samples to decoding success rate is also different. The selection of samples is very important for parameter tuning.
A directional well may create thousands of items of signal data, selecting all of them will lead to too much calculation in parameter tuning and failure of realization. Thereby sample data was selected by well and segment by sequence with the same time interval manually, and the sample length was about 2 times the signal length. For some abnormal drilling conditions, such as pump switch and drill string movement, the data wasn’t selected. Finally, more than 2 000 pieces of sample data were selected from over 20 wells. In addition, some "noise" samples without valid signals were used to test the signal recognition algorithm.
The data contains samples which can't be decoded correctly by field equipment with conventional filtering de-noising algorithm. For all the sample data, the decoding success rate of field equipment was about 90%.
4.2. Parameter tuning
The 10 parameters of the algorithm are related to the decoding success rate of large capacity samples. It is a typical multi-parameter fusion problem because of interaction of the parameters. Special tool software was developed, and step- size scanning was used to divide the mesh to complete parameter tuning.
In order to shorten the tuning time, the wavelet basis function obviously unsuitable was removed and the search was accelerated by using dichotomy. It took thousands of hours to complete automatic scanning work in batches with the high-performance workstation. The combinations of parameter values with the highest decoding success rate were selected as tuned values (Table 3). The automatic decoding success rate of the large capacity samples is 94.9% with this combination of tuned parameters. The result is applicable to the general coding condition of drilling fluid pulse signal previously defined. For non-signal "noise" samples, the algorithm distinguished based on effective synchronization head, instruction minimum and maximum length, effective pulse width and other conditions, with more than 99.5% of the total noise signals identified.
Table 3 Parameter tuning.
| Stage | Parameter | Tuned value |
|---|---|---|
| Frame- synchro- nization | Wavelet basis function | Discrete Meyer |
| Wavelet decomposition level of baseline drift rectification | 10 | |
| Wavelet decomposition level of signal | 8 | |
| Relative rising-edge protruding degree threshold | 70% | |
| Relative falling-edge protruding degree threshold | 70% | |
| Instruc- tion | Wavelet basis function | Discrete Meyer |
| Wavelet decomposition level of baseline drift rectification | 10 | |
| Wavelet decomposition level of signal | 6 | |
| Relative rising-edge protruding degree threshold | 50% | |
| Relative falling-edge protruding degree threshold |
5. Experimental verification
5.1. Sampling
In order to verify whether the samples can represent the characteristics of all the data, the tuned parameters were used to decode all the data of 3 d orientation stage of a directional well, and the decoding success rate was 96.1%. There are about 900 samples in the directional segment, and there is no regularity in the decoding errors. The standard deviation of the decoding success rate of five sample sets (about 180 samples per group) obtained by taking 1 out of 5 samples in turn was about 1%, which shows that the samples reflect the characteristics of all data greatly.
5.2. Parameter influence
As shown in Table 3, the algorithm consists of 10 parameters, of which 6 parameters, including wavelet basis function and decomposition level are discrete, and 4 relative protruding degree thresholds are continuous ranging from 0% to 100%.
In order to study the influence of each parameter on the decoding success rate, the maximum decoding success rate can be obtained by scanning with the software tool according to different values of the parameter, but this method is difficult to realize because of the huge amount of time consumed. Here, the decoding success rate was calculated by changing only one of the tuned parameters, which can reflect the influence of the parameter to a certain extent.
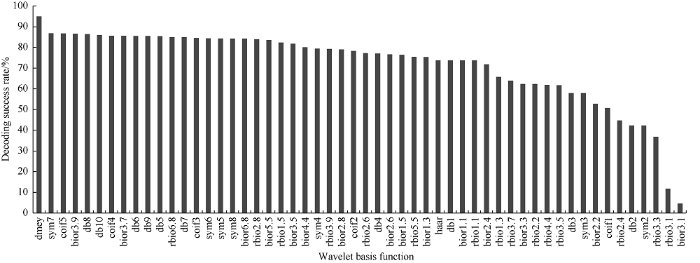
Fig. 8 shows the effect of changing the frame-synchronization wavelet basis function (54 kinds) on the decoding success rate. It can be seen from the figure that, for frame- synchronization wavelet basis function, the highest success rate of discrete Meyer (dmey) decoding is 8.1% higher than sym7 in the second place. Similar calculation of the instruction wavelet basis function show that still dmey has the highest decoding success rate, which is 11.3% higher than db9 in the second place. Apparently, dmey has obvious advantages than the others.
Fig. 8.
Fig. 8.
Influence of frame-synchronization wavelet basis function.
For baseline drift rectification, the change of the instruction baseline decomposition level indicates that: the success rate of decoding below level 8 is 0%, with the increase of level, it reaches a peak of 94.9% at level 10, and then gradually falls back to 92.2% without baseline drift. We can see that the baseline drift rectification increased the decoding success rate by 2.7%. The situation of frame-synchronization baseline decomposition level is similar.
For the decomposition level of instruction signal, the decoding success rate reaches 94.9% when the decomposition level is 6, which is much higher than 49.8% of level 5 and 37.5% of level 7. The situation of frame-synchronization signal decomposition level is similar.
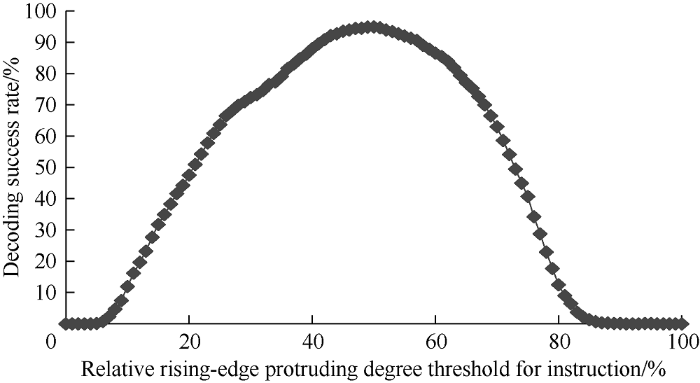
For the relative protruding degree threshold, Fig. 9 shows the effect of relative rising-edge protruding degree threshold of instruction, and the curve becomes flat near the extreme value of 94.9%.
Fig. 9.
Fig. 9.
Influence of relative rising-edge protruding degree threshold for instruction.
If only the relative falling-edge protruding degree threshold is used, the decoding success rate is 61.9%, and the decoding success rate by using both relative rising-edge and falling- edge protruding degree thresholds is 80.2%. That is to say using relative rising-edge protruding degree threshold alone has a higher decoding success rate, which can increase the decoding success rate by 33% at most. The results quantitatively proved test results of other researchers[18].
By analyzing the influence of the parameters, we can see: among the 10 parameters of the algorithm, the selection of wavelet basis function and wavelet decomposition level has some certainty whether it is frame-synchronization or instruction signal processing. Only 3 relative protruding degree thresholds have a greater impact on the success rate of decoding, but it can be solved by automatic threshold adjustment described later. Thus, the robustness of the tuned parameters of the algorithm is guaranteed.
5.3. Algorithm comparison
The large capacity samples were all from field data. The decoding success rate of conventional filter denoising algorithm is about 90%, which is lower than 94.9% of this algorithm. Due to the complexity of various algorithms, it is difficult to make horizontal comparisons directly.
In order to verify the adaptability of the algorithm, 100 samples were selected from each of the five newly drilled wells, and the decoding success rate was 95.2%. The decoding success rate of each well was calculated individually, and the standard deviation was about 2%, which indicates that the algorithm has good adaptability.
The pressure test was done with special positive displacement motor (PDM) experiment stage to verify this algorithm. Comparing with the field signal, the signals in this case had lower pump noise but more severe baseline drift. Over 8 d, more than 2 300 signal sending and receiving tests were carried out, and the automatic decoding success rate of the algorithm was 100%.
5.4. Automatic threshold adjustment
The relative protruding degree threshold parameters were adjusted one by one for the samples that couldn't be decoded in the large capacity samples by using software tool. The number of samples that can be decoded correctly after adjustment increased, and the decoding success rate reached 99.3%. This indicates that the same decoding success rate can be achieved by using the automatic threshold adjustment algorithm.
Bit error rate can be reduced with channel coding in communication field. A check sum of 1 byte is added to the instruction encoding, and checking byte in decoding process to determine whether the decoding is successful or not. If it is not successful, the relative protruding degree threshold is adjusted step by step until the decoding is successful or reaches the threshold limit. Automatic threshold adjustment gets rid of the dependence of 3 relative protruding degree threshold parameters.
6. Conclusions
The de-noising and decoding of signals is an interrelated whole signal processing process and the decoding success rate is a more general evaluation index.
Wavelet forced de-noising is suitable for drilling fluid pulse de-noising. A two-stage de-noising algorithm for frame-synchronization and instruction pulse based on various pulse width has been designed. The algorithm divides the pulse sequence into shorter instruction pulse sequence by identifying wider frame-synchronization pulses, which is helpful to reduce the influence of baseline drift, determine the threshold range of automatic peak detection for signal recognition and improve the decoding success rate.
The relative protruding degree parameter is defined for peak detection. Compared with the absolute threshold judgment, the relative protruding degree parameter can make full use of the change of the peak and distinguish rising-edge and falling-edge, so it has the function of de-noising. For instruction decoding, the rising-edge of the pulse is more important.
Peak detection with different wavelet basis functions will lead to different positions of wave peak. Each instruction pulse is used as a bit-synchronization pulse to decode the subsequent instruction pulse, which can reduce the time-base error accumulation caused by clock drift and improve the decoding success rate.
Large capacity sample was prepared to tune parameters, and the tuned parameters have certain robustness. The automatic decoding success rate of the general coding method is 95%, which is better than the conventional filtering algorithm in the field instrument. The decoding success rate of automatic threshold adjustment algorithm can reach 99%.
Nomenclature
Cj,k, Dj,k—the kth element of the jth level wavelet low-frequency, high-frequency coefficients;
g, h—low-frequency, high-frequency decomposition filter of one dimensional discrete wavelet transform Mallat algorithm, dimensionless;
j—decomposition level of wavelet transform;
k, m—element serial number of wavelet coefficients;
pre, pfe—protruding degree of rising-edge and falling-edge, MPa;
prange—range of protruding degree, MPa;
pRre, pRfe—relative rising-edge, falling-edge protruding degree, %;
Z—integer set.
Reference
Introduction to the theory and technology on downhole control engineering and its research progress
Vibration wave downhole communication technique
Attenuation of microwave transmission in a diameter-variable drill string bore
BlackStar II dual-telemetry MWD tool specification
A new mud pulse telemetry system for enhanced MWD/LWD applications
Pulse signaling for down hole telemetry: US 2010/0188253A1
A review of mud pulse telemetry signal impairments modeling and suppression methods
Eliminating noise of mud pressure phase shift keying signals with a self-adaptive filter
An effective approach for the noise removal of mud pulse telemetry system
Novel two-step filtering scheme for a logging-while-drilling system
DOI:10.1016/j.cpc.2009.04.011 URL [Cited within: 1]
System and method for down hole telemetry: U.S. Patent 8,154,420
Drilling mud signal processing based on wavelet
MWD drilling mud signal de-noising and signal extraction research based on the pulse- code information
Continuous wavelet transformation: A novel approach for better detection of mud pulses
Analysis of discrete wavelet transform algorithm and its general implementation for programming
Mud signal baseline drift rectification in measurement while drilling
Comparative study on mud-pulse signal processing methods