Introduction
Fluid displacement, such as water displacing oil or gas, or oil displacing gas, will increase the fluid density in the pores of rock, and the velocity of seismic wave will increase accordingly when oil field is developed. Conversely, when gas displaces oil or water, or dissolved gas degases in strata, the density of fluid in rock pore will decrease, and the seismic wave velocity propagating through the strata will decrease as well. The pore volume of rocks decreases with increasing reservoir pressure due to production, resulting in an increase of rock density[1]. These changes caused by reservoir development lead to the changes of seismic impedance of the strata and impedance difference between strata, and seismic reflection changes at last. Time-lapse seismic technology came into being then. Time-lapse seismic (also known as 4D seismic) is a technique to predict the distribution of remaining oil or gas of a reservoir in its development stage. By carrying out seismic acquisition at the same area at regular intervals and then processing those seismic data with cross equalization technology to ensure their consistency, those seismic reflection signals which have nothing to do with reservoir variation are kept repeatable, while the reflection signals related to reservoir variation are remained. Finally, the difference of the reflection signals was obtained by subtracting monitoring data from the base data, to monitor the development performance of the reservoir dynamically. Large difference of reflection signals indicates that more reserves are produced, whereas small difference indicates that less reserves are produced. Then the reservoir engineering data, petrophysical information and geological knowledge are combined to evaluate the reservoir comprehensively, so as to optimize the development program and ultimately improve the recovery rate.
The difference of seismic data, which is used to predict remaining oil traditionally, is the absolute difference between seismic data acquired at different times, that is, the difference between monitoring data and base data. By selecting attributes sensitive to absolute time-lapse seismic difference, or carrying out an elastic impedance inversion with time-lapse seismic data, or combining seismic forward modeling and production history of the oil field, the remaining oil distribution of the reservoir can be predicted[2,3,4,5,6,7,8,9,10,11]. But the effect of reservoir thickness on absolute difference is ignored in the traditional method. Based on the study of Zeta oil field in West Africa, a new time-lapse seismic method related to fluid saturation but not affected by reservoir thickness was developed.
1. Overview of Zeta oil field
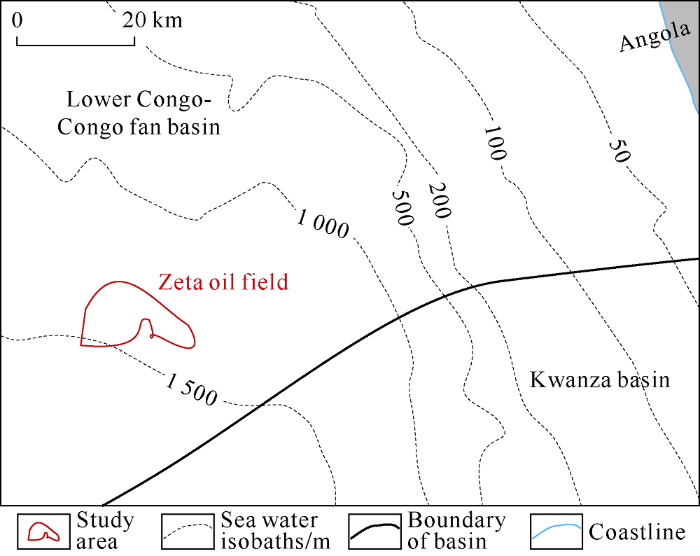
Zeta oil field is located in the deep sea just off the southern end of the lower Congo-Congo fan basin on the west coast of Angola, West Africa, with a water depth of about 1 500 m (Fig. 1). The reservoir of the oil field is the Oligocene turbidite channel sand body composed of largely quartz. The sand layers are 0.8-13.7 m thick, with great lateral variation and a burial depth of less than 1 500 m below the seabed. The structure of Zeta oil field is a fault nose dipping northeast, a complex trap controlled by both structure and lithology. The reservoir is loose and unconsolidated with good physical properties, and the major pay, layer 1# sand body has a porosity of 20%-32%. The crude oil is light (with a density of 0.865 g/cm3 at normal temperature and pressure). The oilfield is developed by waterflooding at an injection-production ratio of 1:1.
Fig. 1.
Fig. 1.
Location of Zeta oil field.
Basic 3D seismic data was acquired before the development of the oilfield, and 3 rounds of monitoring seismic data were acquired successively after it was put into development (corresponding to data volume M1, M2 and M3). The same company undertook the acquisition and processing. In order to ensure that time-lapse seismic data was least disturbed by non-reservoir factors, the technique of equal floating towing cable and GPS positioning control system were adopted for seismic data acquisition, the same sampling time interval and the same acquisition surface element were taken as well, and strict and consistent processing flow and parameters were used in data processing to minimize the influence of non-reservoir factors.
2. Factors affecting the time - lapse seismic difference in Zeta oil field
According to the reservoir type, reservoir characteristics and injection-production ratio of Zeta oil field, the effect of pressure, pore type and porosity on time-lapse seismic data can be eliminated by and large. Generally, temperature change in heavy oil reservoir leads to significant change in time-lapse seismic reflection[12]. The effect of temperature on seismic reflection is negligible in Zeta oil field since its crude oil is light. In a word, the effect of pressure, temperature, pore type and porosity on time-lapse seismic in Zeta oil field can be excluded. Although the reservoir fluids in Zeta oil field only include oil and water, it does not mean that the time-lapse seismic difference is only related to the change of oil and water saturation. Since the thickness of turbidite sandstone in Zeta oil field is generally smaller than seismic tuning thickness (1/4 of wavelength), the size of reflection amplitude is directly related to the thickness of the reservoir in this case. The effect of the above four aspects is merely aimed at a fixed location point. It is feasible to qualitative analyze whether fluid displacement occurs at each point. When analyzing the extent of fluid displacement occurred or quantitatively studying the remaining oil distribution, we need to compare seismic intensity variation of different points, in which reservoir thickness, the most sensitive factor in "thin bed" reflection, must be considered. That is, the effect of reservoir thickness must be removed from the reflection intensity variation so as to get the seismic change caused by fluid saturation change only.
There are few studies on the relationship between reservoir thickness and time-lapse seismic difference. ALVAREZ E et al. proposed that the reservoir must reach a certain thickness when predicting remaining oil saturation by using time-lapse seismic amplitude changes at the fluid interface[9]. Bao Xiangsheng et al. pointed out that the positive or negative difference in average energy of seismic wave was caused by the decrease and increase of seismic velocity in the reservoir, which was not proportional to the thickness of the reservoir, and a thin layer within tuning thickness sometimes made a greater difference than a thick layer[10]. In this work, studies on fluid displacement seismic forward modeling were carried out centering on reservoir thickness and fluid saturation.
3. Gassmann fluid displacement simulation and seismic forward modeling
3.1. Principle of Gassmann fluid displacement
Fluid displacement is to calculate the petrophysical parameters of one fluid state from those of another fluid state[13], which can reflect the effect of pore fluid on seismic velocity and impedance[14]. It provides forward modeling and quantitative analysis tools for 4D seismic research[13]. Fluid displacement usually adopts Gassmann fluid displacement method based on wood equation[13]. Gassmann equation is an important theoretical tool for the study of rock elastic physics. It establishes the relationship between rock bulk modulus, porosity, bulk modulus of pore fluid, bulk modulus of the matrix and bulk modulus of rock-building minerals, and serves as a bridge between rock physical parameters and seismic parameters[14]. Gassmann equation is as follows:
The compressibility of saturated rock can be approximately expressed as:
The following conclusions can be drawn from simultaneous equations (1) and (2): The hard rock with high pore space stiffness is less sensitive to pore fluid, while the soft rock with low pore space stiffness is more sensitive to pore fluid[12].
The studies of WANG Zhijing[1], AVSETH P et al.[14], and ZHOU Yongsheng et al.[13] indicated that for rocks with high porosity and permeability saturated by low-viscosity fluid, the seismic data gathered at 10-200 Hz was close to Gassmann's results. The turbidite sandstone reservoir in Zeta oil field meets this condition.
3.2. Gassmann fluid displacement and petrophysical characteristics of Zeta oil field
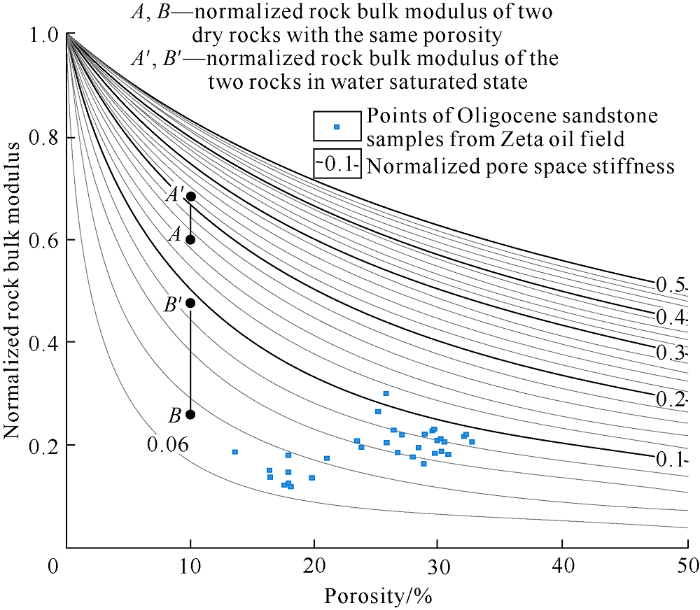
The sensitivity of seismic wave to fluids depends on the porosity and pore space stiffness[14]. Fig. 2 is a chart that reflects the sensitivity of rocks to change of pore fluid[14]. It presents the cross-plot of normalized rock bulk modulus Kdry/Kmin and porosity. Each line in the figure represents different normalized pore space stiffness (Kø/Kmin). The difference between dry rock and water saturated rock is the distance between three isolines at any position in the figure. Point A and point B correspond to two dry rocks with the same porosity and different stiffness, and point A° and point B° correspond to the water saturated state of the two dry rocks respectively. Apparently, the normalized bulk modulus of rock B changes more from dry rock to water saturated state than that of rock A, which means that rock B is more sensitive to the change of pore fluid[14].
Fig. 2.
Fig. 2.
Normalized rock bulk modulus and porosity cross-plot template and distribution of points of Oligocene sandstone samples from Zeta oil field.
The sample points of Oligocene turbidite sandstone in Zeta oil field were distributed in loose rock area with normalized pore space stiffness of 0.06-0.10 when they were casted into the template in Fig. 2. It shows that the Oligocene turbidite sandstone in Zeta oil field belongs to the "soft" rock with low pore space stiffness, which is also supported by the fact that the bulk modulus of rock is much smaller than that of mineral in the following text. These results indicate that the reservoir of Zeta oil field is sensitive to pore fluid change.
The reservoir state before development was taken as the initial state. The initial parameters were input to carry out the Gassmann fluid displacement based on wood equation. Then the process was simulated with seismic forward modeling, and the effect of time-lapse seismic can be obtained at last. Since the water content of all the oil layers drilled before development in Zeta oil field was around 10%, the initial full-oil model of fluid displacement was assigned with oil saturation of 90% and water saturation of 10%, and the final ideal full-water model was assigned with oil saturation of 10% and water saturation of 90%.
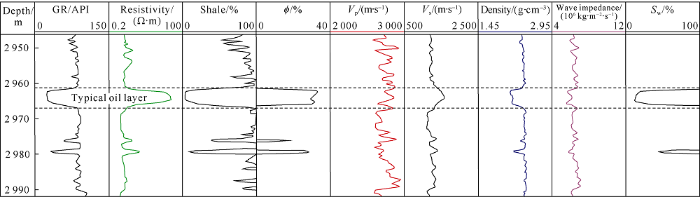
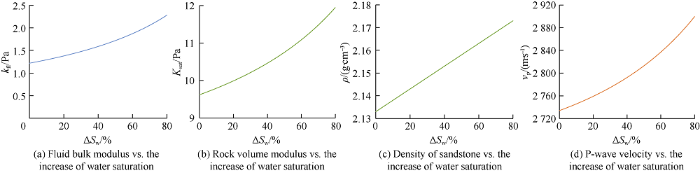
A typical reservoir of layer 1# was selected according to the logging data (Fig. 3), the data of this layer sandstone and that of shale overlying and underlying were picked as the initial model of fluid replacement (full-oil model). Then p-wave velocity, shear wave velocity, density, natural gamma ray value, porosity, fluid and its saturation, mineral components, and fluid saturation of the final state were input to carry out Gassmann fluid replacement to the model. That was to displace the oil in the reservoir by water gradually until the reservoir was full of water. The rock bulk modulus, density, and p-wave velocity, which vary with fluid saturation change, were calculated (Fig. 4). Then seismic forward modeling was carried out after that to obtain the seismic forward modeling profile similar to time-lapse seismic.
Fig. 3.
Fig. 3.
Logs of typical oil layer in Zeta oil field.
Fig. 4.
Fig. 4.
Some elastic parameters vs. the increase of water saturation from the forward modeling of fluid displacement.
In the process of Gassmann fluid replacement, the change of the oil and water saturation of sandstone reservoir leads to changes in the bulk modulus of pore fluid, bulk modulus of the sandstone, and sandstone density, eventually leads to changes in sandstone p-wave velocity and seismic impedance (Fig. 4, Table 1). Meanwhile, the velocity and density of shale remain the same. The above changes of sandstone result in the change of seismic reflection at sand-shale interface contact accordingly.
Table 1 Comparison of parameters between the initial full-oil model and the complete fluid displacement.
| Model state | Kfl/Pa | Ksat/Pa | Vp of sandstone/ (m•s-1) | Density of sandstone/(g•cm-3) | p-wave impedance of sandstone/(103 kg•m-2•s-1) | Vp of shale/ (m•s-1) | Density of shale/(g•cm-3) | p-wave impedance of shale/(103 kg•m-2•s-1) |
|---|---|---|---|---|---|---|---|---|
| Full-oil | 1.22 | 9.62 | 2 733 | 2.133 | 5 829 | 2 696 | 2.354 | 6 346 |
| Full-water | 2.28 | 11.95 | 2 900 | 2.173 | 6 302 | 2 696 | 2.354 | 6 346 |
Because the sandstone impedance is always smaller than that of shale, that is, no matter how thorough the fluid displacement goes, negative reflection is formed at the top interface of sandstone, and positive reflection at the bottom interface, and seismic reflection is strong when sandstone contains oil and weak when sandstone contains water. Therefore, on time-lapse seismic absolute difference profile, at the same location (the reservoir thickness is consistent before and after fluid displacement), the greater the difference, the stronger the oil-water displacement is. This is the petrophysical base for Zeta oil field to monitor reservoir development effect using time-lapse seismic.
3.3. Seismic forward modeling and reservoir thickness effect analysis
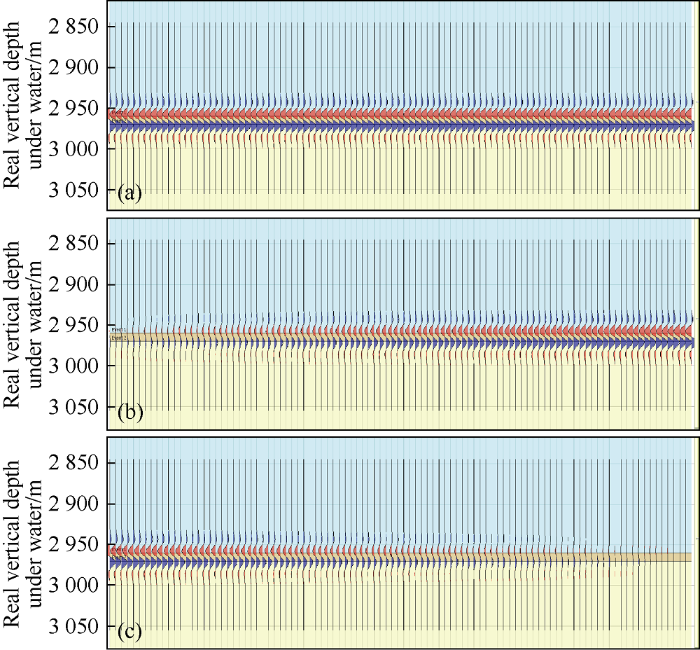
In this study, a total of 5 groups of oil-water displacement models with different reservoir thicknesses were designed. Fig. 5 is one of the models in this study with reservoir thickness of 10 m. Ricker wavelet was used. The main frequency was 35 Hz, which is the main frequency of the seismic data. In Fig. 5, the pore fluid in the sandstone reservoir in Fig. 5a is full of oil, and the model in Fig. 5b is a fluid displacement progressive model, in which the fluid in the reservoir uniformly transfers from full-oil to full-water from the right of the model to the left. It can be seen that the seismic reflection of the far right side of the model in Fig. 5b is exactly the same as that in Fig. 5a, and the seismic reflection from right to left gradually weakens, which indicates that the seismic impedance difference between the reservoir and the upper and lower shale gradually decreases. Fig. 5c shows the seismic reflection residuals of Fig. 5a model and Fig. 5b model (the absolute difference, that is, the difference of traditional time-lapse seismic). It can be seen that the residual corresponding to the right-most full-oil is 0, while the residual is the largest at left-most full-water case.
Fig. 5.
Fig. 5.
Forward modeling of time-lapse seismic. a and b are seismic forward modeling of a thin layer sandstone model with a thickness of 10 m in the background of shale, the sandstone reservoir in
This forward modeling of time-lapse seismic shows that, for unconsolidated turbidite sandstone reservoirs about 10m thick, the absolute difference of time-lapse seismic increases gradually as the oil saturation decreases and water saturation of the reservoir increases gradually. The absolute difference of time-lapse seismic reaches the largest when the fluid changes from full-oil to full-water. The same conclusion can be obtained from seismic forward modeling of fluid displacement in unconsolidated sandstone reservoirs of 5 m, 20 m, 25 m and 30 m thick.
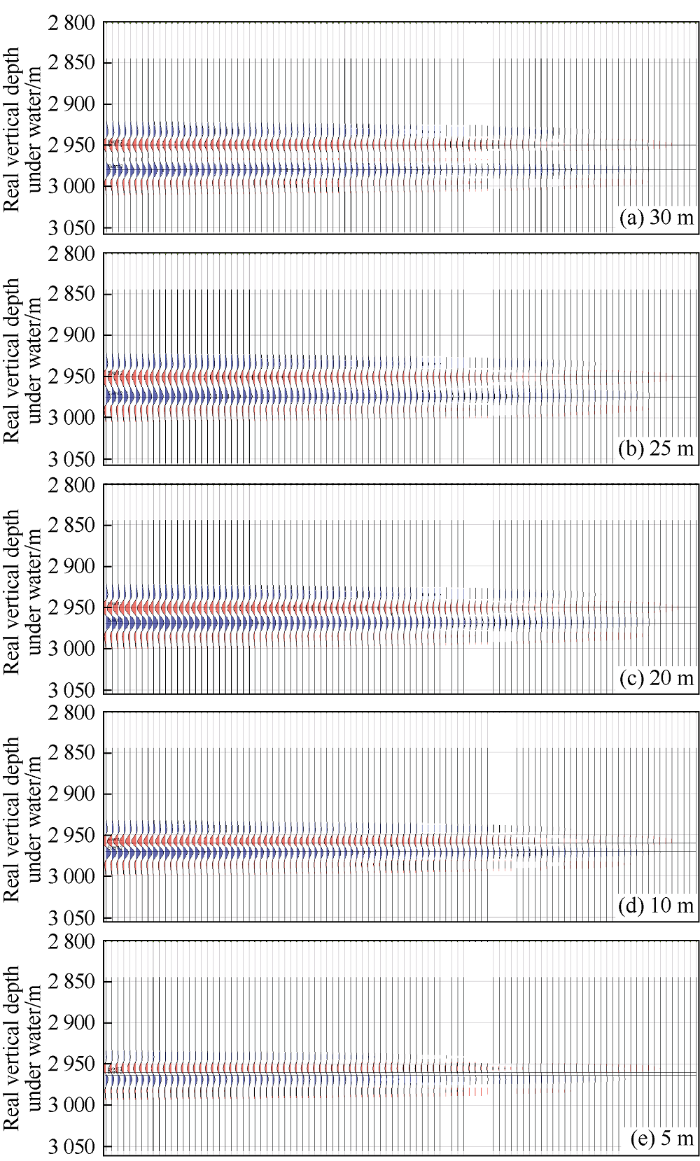
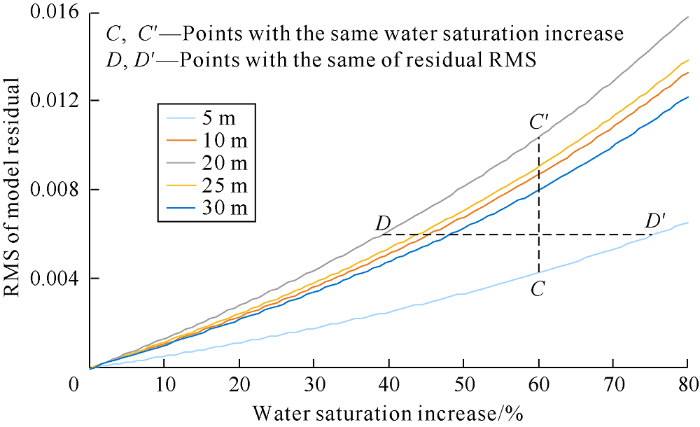
The root-mean-square amplitude (hereinafter referred to RMS) of each residual was extracted from the window with the same length covering the top and bottom of the sandstone layer, and it is shown in Fig. 6 with the same range. It is found that the residual strength is significantly different with different thicknesses of reservoirs. Furthermore, the relationship curves between the increase of water saturation and the RMS of the absolute time-lapse seismic difference of each seismic trace from the above five models with different reservoir thicknesses were plotted in Fig. 7. It can be seen that the difference of the five curves gradually widens with the increase of water saturation. When the increase of water saturation of the reservoir is the same, the absolute difference of time-lapse seismic for different thicknesses are different, as shown in Fig. 7 from C to C°. While for the same absolute difference of time-lapse seismic, the increase of water saturation for different reservoir thicknesses are also different, as shown in Fig. 7 from D to D°. This indicates that the absolute time-lapse seismic difference is not only affected by fluid saturation, but also related to reservoir thickness.
Fig. 6.
Fig. 6.
Seismic reflection residues of 5 fluid displacement models and full-oil models different in thickness. Residues are shown within the same range. In each model, the fluid in the reservoir uniformly transfers from full-oil to full-water from the right of the model to the left.
Fig. 7.
Fig. 7.
Relationship of residual RMS and water saturation increase in fluid displacement models of sandstone with different thickness.
It is known to all that seismic reflection is the comprehensive response of seismic waves superimposed by the reflections where seismic wavelet reflects at each underground interface. The top and bottom of the sandstone reservoir in shale are two interfaces of equal reflection coefficient but opposite direction. When the thickness of sandstone is equal to the tuning thickness, the amplitude of the reflection at the top and bottom interface is maximized due to the mutual interference of the two reflections. When the thickness is slightly larger or smaller than the tuning thickness, the reflection amplitude is larger than that of a single interface because of the interference as well. When the sandstone thickness is less than the tuning thickness, the reflection amplitude decreases with the decrease of sandstone thickness.
Based on the velocity of sandstone in the model (about 2733 m/s) and the dominant frequency of the seismic data (35 Hz), the calculated tuning thickness of the models is about 20 m. In Fig. 7, for the same water saturation increment, the RMS of the residual of the model with a thickness of 20 m is always larger than models of other thicknesses, while the 5 m sandstone model with the smallest thickness is always the smallest. Reservoirs 25 m and 10 m thick are still subject to enhanced interference by the reflection from the top and the bottom interfaces. Reservoir 25 m thick is subject to greater interference, and the position of its curve is higher than that of 10 m model. Their strengths are greater than that of 30 m model, in which the reflections of the top and the bottom are completely separated. Under the same increase of water saturation, the residual RMS of the models rank in the order of 20 m, 25 m, 10 m, 30 m and 5 m. In the initial full-oil models, the model of 20 m thick reservoir (equivalent to the tuning thickness) has the largest reflection amplitude and the largest RMS, and the model of 5 m thick reservoir has the smallest reflection amplitude and the least RMS. The RMS values of the initial full-oil models of different thicknesses from large to small in sequence are: 20 m, 25 m, 10 m, 30 m, and 5 m. That is, the energy of seismic reflection residues (absolute difference of time-lapse seismic) is also strong after fluid displacement of the same degree occurs in the full-oil model with strong seismic reflection, and it is still weak after fluid displacement of the same degree occurs in the full-oil model with weak seismic reflection. It is only the thickness that makes the seismic reflection intensity of these initial full-oil models different. This further indicates that the absolute difference of time-lapse seismic intensity is directly related to the reservoir thickness for a certain water saturation increment and also follows the law of "tuning effect" and "thin bed" reflection rule.
Therefore, the existence of absolute difference of time- lapse seismic can only indicate that fluid displacement has occurred, but the degree of fluid displacement cannot be determined. The greater absolute difference does not necessarily mean the more thorough the fluid displacement. It is just because the magnitude of the absolute difference of time-lapse seismic is closely related to the thickness of reservoir, and the reservoir thickness of Zeta oil field is generally less than the tuning thickness and varies fast laterally, the absolute difference of time-lapse seismic is not available in Zeta oil field to calculate the change of reservoir fluid saturation and quantitatively predict the remaining oil distribution.
4. Quantitative prediction of remaining oil based on time-lapse seismic “relative difference method”
In order to quantitatively characterize the volume of remaining oil, based on the improvement of traditional time- lapse seismic, the concept of time-lapse seismic “relative difference” was proposed in this study, that is, the ratio between a monitoring seismic attribute and the same attribute of base seismic data (In this paper, RMS is taken as an example).
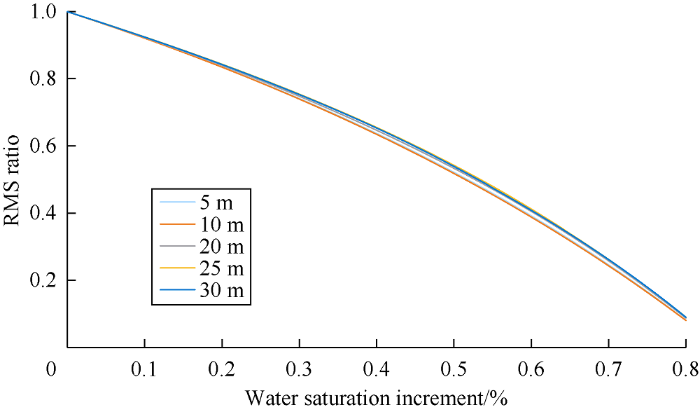
Using the data of the above five forward modeling simulations, the ratio of RMS value of the fluid displacement of each thickness model to that of the full-oil model (in other words, the absolute difference gained from time-lapse seismic in traditional way was converted to relative difference) was calculated, and then the ratio was intersected with the fluid saturation increment (Fig. 8). Fig. 8 shows that the cross-plot curves of different thickness reservoirs almost completely overlap, that is, the relative difference in time-lapse seismic is only related to fluid saturation and has nothing to do with reservoir thickness. In other words, when the same degree of fluid displacement occurs in the reservoir, the relative changes in the seismic reflection intensity of reservoirs of different thicknesses are equal. Conversely, if the relative changes in seismic reflection intensity are the same, regardless of the thickness of the reservoir, the extent of fluid displacement within the reservoir is the same. According to this, the remaining oil in the deep-sea unconsolidated sandstone reservoir of Zeta Oil field can be predicted quantitatively. The idea of the prediction method is as follows: Firstly, the Gassmann fluid displacement seismic forward modeling is conducted to find out the relationship between the relative differences of time-lapse seismic and the increase of water saturation. Secondly, the relative difference of RMS in the target interval between the monitoring seismic in each period and basic seismic is calculated, and then converted to the change of the reservoir water saturation (or oil saturation) on the plane, then the remaining oil distribution of the reservoir can be obtained. Finally, the remaining oil reserves are calculated by combining with the reservoir thickness distribution data etc.
Fig. 8.
Fig. 8.
Relationship of RMS ratio and water saturation increment in fluid displacement model of sandstone with different thickness.
Time-lapse seismic relative difference method is applicable to deep-sea unconsolidated sandstone reservoirs in which the effects of pressure, temperature, pore type and porosity on seismic reflection can be excluded. It is applicable to both thick and thin reservoirs and is a method for quantitative prediction of remaining oil. It overcomes the limitations of traditional methods not applicable to unequal thickness reservoirs within seismic “thin bed” category. Comparing with the traditional qualitative methods predicting remaining oil distribution, this method has obvious advantages (Table 2).
Table 2 Comparison between time-lapse seismic “relative difference method” and traditional remaining oil prediction methods.
| Content | Seismic difference evaluation method | Basic idea | Remaining oil prediction method | Nature | Solved problem | Scope of application | Problems |
|---|---|---|---|---|---|---|---|
| Traditional method (absolute difference method) | The difference between monitoring seismic and basic seismic, which is absolute difference | The difference means that fluid displacement occurs. The greater the difference, the more complete the fluid displacement | Select attributes sensitive to the time-lapse seismic absolute difference, or perform elastic wave impedance inversion, or combine forward modeling | Qualitative | For reservoirs with different thicknesses within the thickness of thin bed, the extent of fluid displacement can only be roughly inferred qualitatively | The reservoir thickness is less than the tuning thickness but uniform or the reservoir thickness is greater than the tuning thickness, and the effects of pressure, temperature, pore type and porosity on seismic can be excluded | Ignoring the effect of the thickness, it is not suitable for unequal thickness reservoirs smaller than the tuning thickness; it is not easy to identify the remaining oil in the relatively thick layer within the thin bed category, resulting in the omission of remaining oil reserves |
| Relative difference method | The ratio of monitoring seismic to basic seismic, which is relative difference | The absolute difference of time-lapse seismic is not only related to the change of fluid saturation, but also closely related to the thickness of the reservoir; the relative difference of time-lapse seismic is not affected by thickness, but only related to the change of fluid saturation. The greater the relative difference in time-lapse seismic, the more thorough the fluid displacement | Carry out the Gassmann fluid displacement seismic forward modeling according to the actual logging data, and establish the relationship between the relative differences of time-lapse seismic and the increase of water saturation. Calculate the relative difference of the actual time-lapse seismic and then convert it to the change distribution of the reservoir oil saturation. Predict the remaining oil distribution and calculate the remaining oil reserves by combining with the reservoir thickness distribution data etc | Quantitative | Quantitatively calculate the change of water saturation, predict the distribution of the remaining oil, and quantitatively calculate the remaining oil reserves | Applicable to both thick and thin layers of deep-sea unconsolidated sandstone reservoirs, in which the effect of pressure, temperature, pore type and porosity on seismic can be excluded | No actual research work has been carried out on non-deep sea unconsolidated sandstone reservoirs, but the relative difference method may be a more correct research direction |
5. Application in Zeta oil field
According to the conditions of geology and development of Zeta oil field and model values, the water saturation increment in Fig. 8 was converted into oil saturation, and the cross-plot of time-lapse seismic relative difference and oil saturation was compiled. The fitting relationship is as follows:
So=0.471 3r2+0.348 1r+0.074 4 (3)
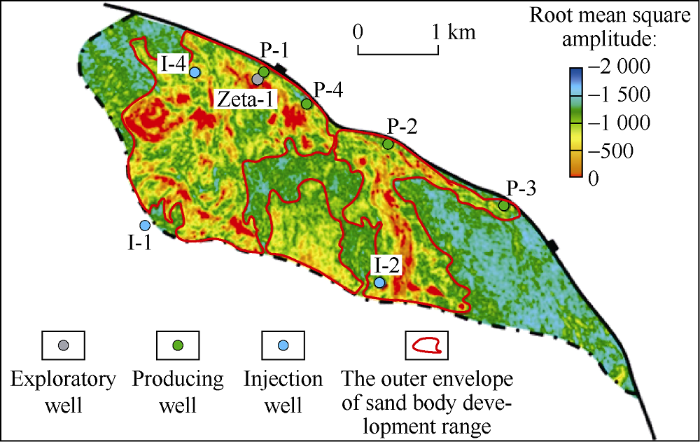
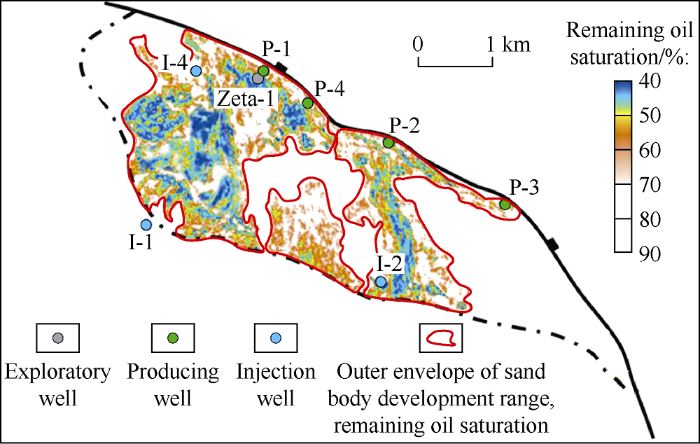
Taking the third monitoring seismic (acquired in 2013) of Zeta oil field as an example. RMS of layer 1# reservoir of the monitoring seismic and the basic seismic (collected in 2000) were calculated, and the ratio of these two values was worked out. The value of ratio is the relative difference, r. The So (reservoir oil saturation) was obtained by substituting r into equation (3). Comparing with the reservoir layer 1# sand body distribution map (Fig. 9), So data in the sand body development range was the oil saturation distribution of the remaining oil in layer 1# of Zeta oil field during the third stage of monitoring seismic acquisition in 2013 (Fig. 10).
Fig. 9.
Fig. 9.
Distribution of Layer 1# sand body in Zeta oil field.
Fig. 10.
Fig. 10.
Distribution of the remaining oil saturation in layer 1# of Zeta oil field during the phase 3 monitoring seismic acquisition in 2013.
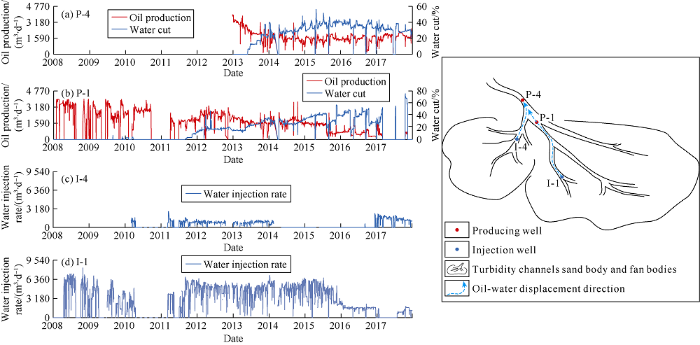
Comparing with the production history data of the oilfield since it was put into development, a brief analysis was made by taking four wells (P-1, P-4, I-1, and I-4) in the west of the oilfield as examples. The operator made the western sand body development area of the oilfield as an injection-production well group, and designed and drilled four development wells. The wells are produced by “multi-layer commingled production manner and separate layer water injection”. Among them, well P-1 and P-4 are two producing wells at structural high, and well I-1 and I-4 are two injection wells. Well I-1 is out of the reservoir boundary and in the lowest structure position, in which the entire layer 1# sandstone drilled is water layer; Well I-4 is located in the middle to high part of the structure, in which the entire layer 1# sandstone drilled is oil layer. Water had been injected to layer 1# of Well I-1 continuously from March 2008 to January 2017 when it was shut down; In Well I-4, water was injected into layer 2# from March 2010 to February 2014, the layer 2# was plugged in December 2016 and water began to be injected into layer 1# (Fig. 11a), that is, during the phase 3 monitoring seismic acquisition in 2013, water wasn’t injected into layer 1# of Well I-4 yet.
Fig. 11.
Fig. 11.
Production curves of the 4 wells in the west part of Zeta oil field and schematic diagram of the connectivity and injection-production linkage of layer 1# sand body.
According to the change of oil production and water cut of Well P-1 and P-4 after water was injected in layer 1# of Well I-1 and I-4 (Fig. 11a), it is inferred that the injection-production linkage of layer 1# sand body of the four wells in the west part of the oilfield is as follows: the water injection in Well I-1 contributes to both Well P-1 and P-4, and the water injection in Well I-4 only contributes to Well P-4. The sand body connection relationship of the four wells is as follows: all the layer 1# sand bodies of the four wells are connected; Well P-4 is at the highest part, and Well P-1 and I-1 are a branch of the sand body connected with Well P-4. Well I-4 is another branch that communicates with the sand body of Well P-4; the intersection of the two sand bodies is higher than that of Well P-1 (Fig. 11b). This understanding has been recognized by the operator. The contribution of Well I-4 to Well P-4 production in 2017 was 382m3/d, which was approximately 10% of its production. This conclusion indicates that there was no oil-water displacement in layer 1# sand body of Well I-4 and the surrounding before water was injected into layer 1# of Well I-4. Fig. 10 shows that the oil saturation of layer 1# around Well I-4 in 2013 was above 80%, which is consistent with the above analysis results, and is also consistent with the actual situation of the average water cut of about 10% in layer 1# before the development of this area.
6. Conclusions
The absolute difference of time-lapse seismic is not only related to fluid saturation changes, but also closely related to the thickness of reservoir. Given the same change of fluid saturation, the absolute difference of time-lapse seismic conforms to the law of “tuning effect” and “thin bed” reflection rules. For unconsolidated sandstone reservoirs for which the effects of pressure, temperature, pore type and porosity on seismic can be excluded, the traditional method of predicting remaining oil with absolute time-lapse seismic difference is only applicable to the reservoirs with thicknesses less than the tuning thickness but equal, or with thickness greater than the tuning thickness.
The relative difference of time-lapse seismic is not affected by the thickness of reservoir but only related to the change of fluid saturation. For unconsolidated sandstone reservoirs for which the effects of pressure, temperature, pore type and porosity on seismic can be excluded, the relationship between the relative difference and the increase of water saturation established on seismic forward modeling after Gassmann fluid displacement simulation, can be directly used to predict the remaining oil distribution and quantitatively calculate the remaining oil reserves based on the thickness of the reservoir etc. The time-lapse seismic relative difference method is applicable to both thick and thin reservoirs and the application in Zeta oil field in West Africa has proved the effectiveness.
Nomenclature
Kdry—bulk modulus of the dry rock frame, Pa;
Kfl—bulk modulus of the pore fluid, Pa;
Kma—bulk modulus of the matrix, Pa;
Kmin—bulk modulus of rock minerals, Pa;
Ksat—saturated bulk modulus of the rock, Pa;
ϕ—porosity, %;
Kø—pore space stiffness, Pa;
So—oil saturation, %;
r—relative difference, RMS ratio of fluid displacement model to initial model (or monitoring seismic to basic seismic), dimensionless;
vp—p-wave velocity, m/s;
ρ—density, g/cm3;
∆Sw—change of water saturation, %.
Reference
Fundamentals of seismic rock physics
DOI:10.1190/1.1444931 URL [Cited within: 2]
Methodology and application of 3.5D seismic exploration
Time-lapse seismic interpretation on inversed impedance data of thin inter-layer reservoir
Towed streamer time-lapse seismic survey design: A case study
A receiver motion correction method for streamer data
History matching of production and 4D seismic data: Application to the Girassol field, offshore Angola
Enhanced dynamic interpretation from correlating well activity to frequently acquired 4D seismic signatures
DOI:10.1190/1.3640528 URL [Cited within: 1]
Turbidite reservoir compartmentalization and well targeting with 4D seismic and production data: Schiehallion Field
DOI:10.1144/SP347.7 URL [Cited within: 1]
Quantifying remaining oil saturation using time-lapse seismic amplitude changes at fluid contacts
DOI:10.1144/petgeo2016-037 URL [Cited within: 2]
Relationship between the difference in average energy of time- lapse and the change of reservoir velocity
Time-lapse seismic matching inversion in water flooding reservoir: A case of deep-water fan in the Oilfield A, West Africa
4D seismic qualitative interpretation for water injection monitoring: Case study in Southeast Asia
Research on fluid substitution method and its application
Quantitative seismic interpretation