Introduction
The intrinsic permeability of porous media (hereinafter referred to as permeability) is determined by its pore structure[1,2]. In the field of oil and gas exploitation, permeability is crucial for reservoir evaluation and development[3]. By using analytical method[4,5], experimental method[6,7,8,9,10] and simulation method[11,12,13,14], researchers have established relations between permeability and pore structure parameters, in which permeability is linked with porosity (or connected porosity), pore radius, tortuosity, specific surface area, and solid particle size etc. However, these relations differ greatly, and are only applicable to isotropic and homogeneous conventional reservoirs[15]. Compared with conventional reservoirs, pore structure of unconventional reservoirs (including tight sandstone and shale, etc.) has the following characteristics: (1) Developing micro/nano-meter pores[16] with complex pore morphology[17,18,19,20]; (2) Strong anisotropy at pore-scale[21,22,23]; (3) Strong pore-distribution heterogeneity[17, 24-25]. Pore anisotropy and pore-distribution heterogeneity significantly affect the permeability of porous media[22-23, 26-27], and are important features of unconventional reservoirs different from conventional reservoirs. Gu et al.[28] proposed a calculation model of pore-scale anisotropy through neutron scattering. But with neutron scattering intensity needs to be measured, its applicability is greatly restricted. Soon afterwards, based on morphological principle, Wang et al.[26] proposed quantitative models of pore anisotropy and pore-distribution heterogeneity in porous media with better applicability.
So far, there have been few quantitative studies on anisotropy and pore-distribution heterogeneity in porous media reported. The influence mechanism of anisotropy and pore-distribution heterogeneity on permeability of porous media is still unclear[21]. There are no reports on studies of quantitative evaluation of pore-scale anisotropy and heterogeneity by reconstructing 3D digital cores based on micro-CT images. With the development of imaging technology, micro/nano-meter pores and their connectivity in porous media can be directly observed by physical experimental method. Meanwhile, QSGS algorithm can be used to construct anisotropic and heterogeneous porous media efficiently, to reflect most of the morphological complexity of natural porous media[29]. The Lattice Boltzmann method (LBM) can directly and efficiently handle the interaction of fluid-fluid and fluid-solid[30] to realize pore-scale simulation of porous media[26, 31]. All of these provide conditions for studying the influence mechanism on permeability of unconventional reservoirs. In this study, micro-CT scanning, QSGS algorithm and LBM were combined to reveal the mechanism of pore-scale anisotropy and pore-distribution heterogeneity acting on the permeability of porous media.
1. Pore structure of tight sandstone
1.1. Construction of three-dimensional digital cores
(1) The experimental results of casting thin sections, scanning electron microscopy and X-ray on four tight sandstone samples (H6-1, H6-2, H106-1 and H106-2) selected from a gas reservoir in Sichuan Basin show that pore space in tight sandstone is composed of intercrystalline micropores, intergranular pores, intragranular/intergranular dissolution micropores and intergranular microcracks; their components are mainly lithic feldspar sandstone and feldspar lithic sandstone, mostly medium and fine-medium in grain size, some medium-coarse and a small amount silt level in grain size. The cements in them consist of mixed illite/smectite layer, illite and clay matrix.
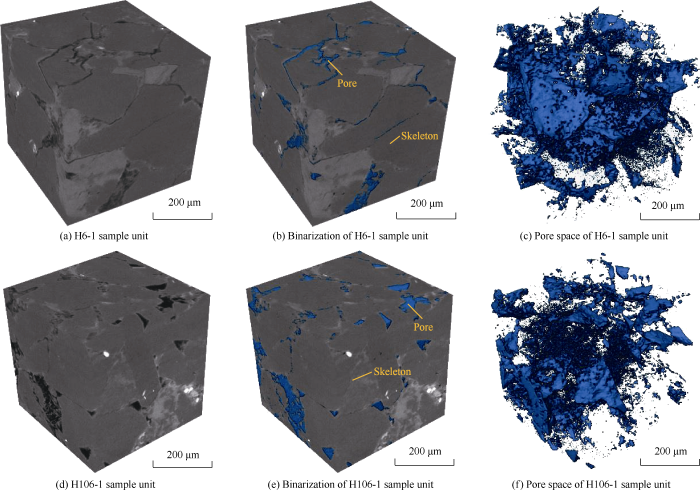
(2) Micro-CT scanning experiments were conducted on small core plugs (actual physical size in Table 1) drilled from the end faces of the samples (at test voltage of 150 kV, electricity current of 90 μA, scanning time of 120 min, image resolution of 620 nm). The scanning sequence was consistent with the axial direction of the samples. Then, with special software, two-dimensional CT images of samples were processed by median filtering and binarization to obtain rock skeleton and pore space accurately. Then microstructure image of samples was completed with image incision. Fig. 1 shows the 3D images of samples H6-1 and H106-1 (800 pixels×800 pixels×800 pixels, corresponding physical dimension of 0.496 mm×0.496 mm×0.496 mm) before and after binarization as well as pore space of them. It can be seen that pores in them are very complex and irregular in shape.
Table 1 The actual physical size of drilled rock samples.
| Sample | Diameter/mm | Height/mm | Sample | Diameter/mm | Height/mm |
|---|---|---|---|---|---|
| H6-1 | 1.085 | 0.663 | H106-1 | 1.099 | 0.649 |
| H6-2 | 1.113 | 0.612 | H106-2 | 1.113 | 0.646 |
Fig. 1.
Fig. 1.
3D image of tight sandstone samples based on CT image.
(3) Numerical reconstruction was carried out to establish 3D digital cores of them, the calculated porosity of them are 2.60%, 4.49%, 4.51% and 2.61% respectively.
1.2. Quantitative evaluation of anisotropy and heterogeneity
Based on the established 3D digital cores, models (equa-tions (1) and (2)) proposed by Wang et al.[26] were used to quantitatively evaluate pore anisotropy and pore-distribution heterogeneity of the samples.
The anisotropy factor is defined as the ratio of the sum of width of all pores to the sum of height of all pores in porous media, and the strength of anisotropy is directly proportional to A (A=1 represents isotropy). The pore-distribution heterogeneity factor is expressed as the relative standard deviation of porosity of a cell block (depending on observed scale). The strength of pore-distribution heterogeneity is proportional to H.
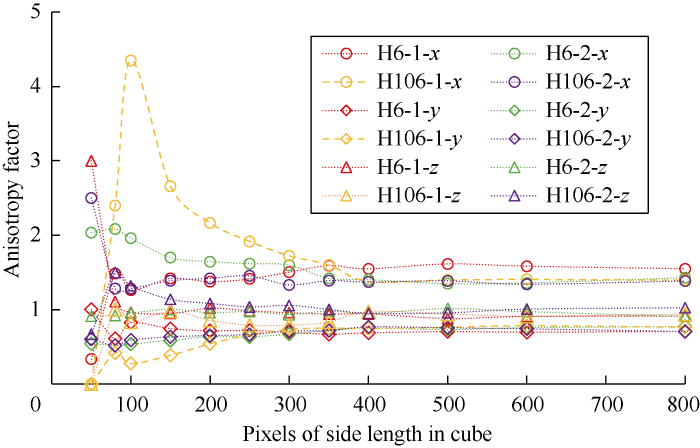
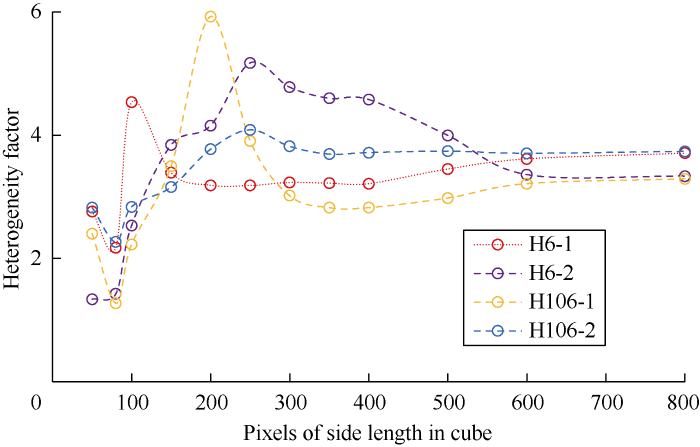
The line-spacing was set at 5 lattices. The length, width and height of the cell blocks were all set at 25 lattices. The pore-scale anisotropy and heterogeneity of four tight sandstone samples were calculated, while the relationships of anisotropy factor and heterogeneity factor with side length of digital cores obtained are shown in Figs. 2 and 3 respectively. The figures show although the 4 samples have some differences in porosity, they have similar variation in pore-scale anisotropy and pore distribution heterogeneity. Fig. 2 shows that the anisotropy tends to be stable as side length of the digital cores reaches 300 pixels, and A value in the x, y and z directions are from 1.38 to 1.55, 0.70 to 0.77 and 0.91 to 1.02 respectively (the axial direction of rock sample is defined as x, the direction perpendicular to x in the horizontal plane is defined as y, and the direction perpendicular to the plane formed by x and y is defined as z). That is to say, the tight sandstone samples have the largest anisotropy factor in the x direction (defined as the mainstream direction), while that in the other two directions are similar. Fig. 3 shows that the heterogeneity of the tight sandstone samples tend to be stable at H value between 3.29 and 3.74 as the side length of the digital cores reach 600 pixels.
Fig. 2.
Fig. 2.
The relationship of pore-scale anisotropy factor with side length of the digital core.
Fig. 3.
Fig. 3.
The relationship of pore-distribution heterogeneity factor and side length of the digital core.
2. LBM simulation of 3D random porous media
According to above analysis, micro-CT image can reflect the 3D morphology of pore space and interpore connectivity in rocks. However, due to the limitation of resolution, it is usually difficult to completely obtain nanometer pores in unconventional reservoirs with micro-CT scanning, resulting in disconnected pore space in established digital cores. Therefore, based on the analysis results of pore scale anisotropy and pore distribution heterogeneity of tight sandstone, 3D model of anisotropic, heterogeneous porous media can be constructed by QSGS method. Then fluid migration can be simulated by using multiple relaxation time Lattice-Boltzmann (MRT-LB) model with three dimension and nineteen discrete velocity directions (D3Q19), and study the influence mechnism on permeability.
2.1. Constructing porous media
2.1.1. QSGS method
The detailed process of constructing 3D porous media by QSGS method is as follows[29]: (1) Set the sturctual area and randomly distribute solid-phase growth cores (Cs), while the distribution probability (Pcd) is less than the porosity (ϕ) of the porous media constructed; generating random number of [0,1] by using random number generator and the node with random number smaller than Pcd is designated as solid-phase growth core; (2) Setting the growth speed (Pk, k stands for growth direction of solid phase) in different directions and generating random number of [0,1]; when the random number of Cs node is less than Pk, solid phase grows towards the neighbor point in the k direction; there are 26 growth directions in total, including 6 lateral directions, 12 diagonal directions and 8 diameter directions; when the growth velocity in all directions are same, isotropic porous media can be obtained, while the anisotropic porous media can be obtained when growth velocity in different directions are different; (3) Repeating step (2) until the specified porosity is achieved.
To study the influence of pore-distribution heterogeneity on permeability of 3D porous media better, two separate construction processes were applied[26]: (1) Refined structure generated the smaller solid phase with the distribution probability of solid-phase growth cores of Pr and porosity ofφR; (2) Coarse structure generated larger solid phase with the distribution probability of solid-phase growth cores of Pc far less than Pr. By combining the two construction processes, nodes occupied by any process are set as solid phase until the specified porosity is achieved.
2.1.2. Deleting isolated pores
In the constructed 3D porous media, there are isolated pores (or dead pores) and connected pores. Connected pores are the channels for fluid migration in porous media. The four-connected region labelling algorithm[32] can be used to remove isolated pores: (1) Scanning pores and solid phase in porous media and the label number of pores is appointed to 0; (2) Checking the adjacent pore pixel points of each pore pixel point in the east, south, west, north, upper and lower directions; if all adjacent pore pixel points are not marked, a new label number is set to this pixel point and increases from 1 with no repeat; if only one adjacent pore pixel point is marked, the pore pixel point is set to the same label number; if two or more adjacent pore pixel points have been marked, the pore pixel point is set to the minimum label number among them; (3) Checking all pore pixel points in the 3D porous media and using the minimum label number to mark interconnected pore pixel point; (4) Checking whether the pore space represented by each label number is connected with the inlet and outlet of 3D porous media at the same time.
2.2. LBM model and validation
Compared with single relaxation (SRT) model, the collision operator in MRT model introduces multiple relaxation time, so it has higher computation accuracy and better stability, and is more suitable for studying seepage in porous media. The evolution equation of MRT-LB model is[30]:
where M is transformation matrix of 19×19[33]; M-1 is the inverse matrix of M, which can be obtained by gaussian elimination method. S is diagonal matrix:
where nonzero elements in matrix represent different physical quantities (such as, energy moment, energy square moment, energy flux moment and stress tensor moment, etc.), and they are defined as[34]:
In D3Q19 model, the equilibrium distribution function can be expressed as[34]:
Density, velocity and kinematic viscosity of macroscopic fluid can be expressed as respectively:
In LBM simulation, fluid flow is laminar with small Re value. According to Darcy's law, the permeability of 3D porous media can be calculated[1]:
The tortuosity of 3D porous media can be obtained[35]:
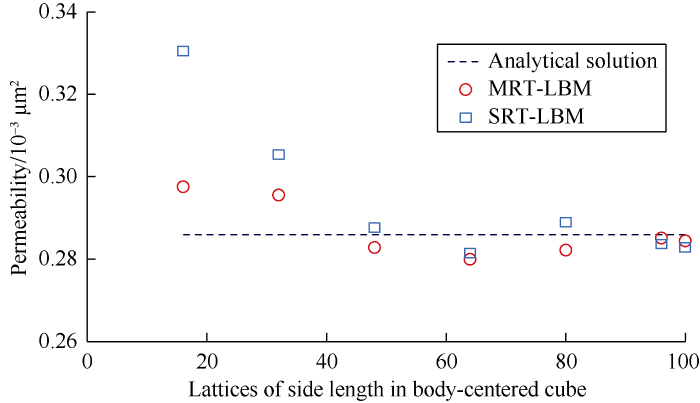
To verify the accuracy of LBM algorithm, D3Q19 MRT and D3Q19 SRT models (τR=1) were used to simulate fluid migration in body centered cubic. The porosity and side length of body centered cube were set at 58.2% and 320 nm respectively, while grid numbers were set at 16×16×16, 32× 32×32, 48×48×48, 64×64×64, 80×80×80, 96×96×96 and 100× 100×100 respectively. Equation (8) was used to calculate the permeability of body centered cube based on simulation results, which was compared with the analytical solution of permeability[36] (Fig. 4). Fig. 4 shows that the accuracy of MRT model is higher than SRT model. Due to the deviation of solid sphere radius in body centered cube for simulation from theoretical value[26], the simulation results will approach the analytical solution as grid number increases. But even at grid number of only 16×16×16, the relative deviation between the simulation result of MRT model and analytical solution is only 4.09%, which indicates MRT model can accurately simulate fluid flow in 3D porous media.
Fig. 4.
Fig. 4.
Comparison of permeability from LBM simulation with that from analytical solution.
2.3. The simulation results
2.3.1. Simulation of 3D anisotropic porous media
Based on the analysis results of pore scale anisotropy in tight sandstones, and avoiding the impact of significant changes in pore morphology on simulation results, the growth velocity of solid phase in x, y and z directions were set differently (y and z directions were the same) in QSGS algorithm to construct 3D anisotropic porous media (parameters listed in Table 2). To exclude the effect of pore structure randomness on permeability, 10 random porous media models were constructed with the same group of construction parameters, and a total of 180 models of 3D anisotropic porous media were generated.
Table 2 Basic parameters in QSGS algorithm and MRT-LBM simulation.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pcd | 0.002 5, 0.005, 0.01 | Fluid | water |
| ϕ | 30% | Temperature | 333 K |
| Mesh number | 64×64×64 | Inlet pressure | 20 MPa |
| δL | 10 nm | Inlet density | 983.1 kg/m3 |
| Dx | 0.01 | Outlet density | 983.099 997 6 kg/m3 |
| Dy | Dx, Dx/2, Dx/4, Dx/6, Dx/8, Dx/10 | Dynamic viscosity | 0.000 469 9 Pa•s |
| Dz | Dz=Dy | Pressure gradient | 0.102 8 MPa/m |
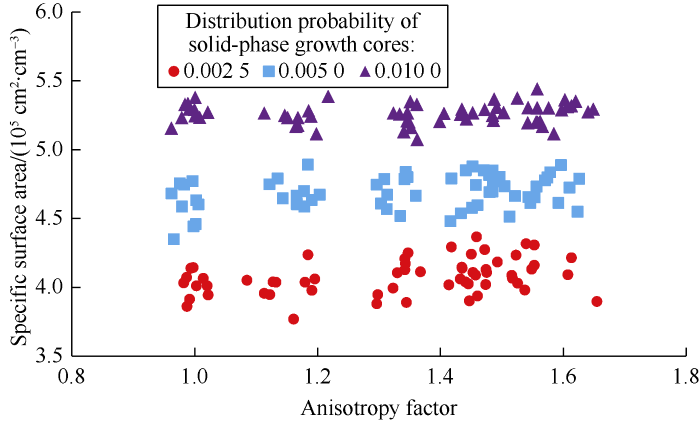
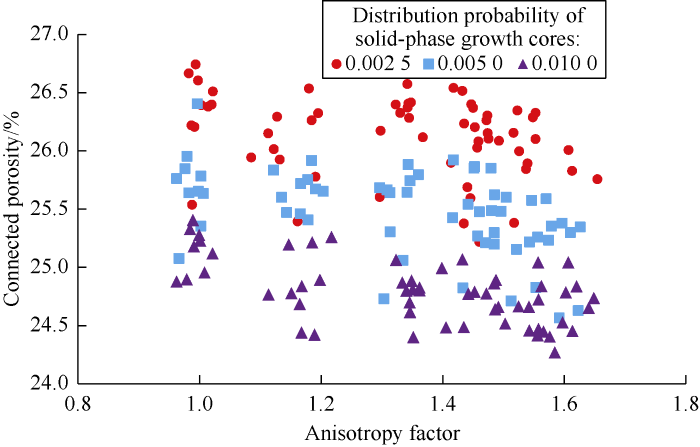
Removing the isolated pores and the line-spacing was set at 4 lattices. Equation (1) was used to calculate the anisotropy factor of porous media. The relationships of connected porosity and specific surface area with anisotropy of 3D anisotropic porous media were obtained (Figs. 5 and 6). The figures show that the anisotropy factor of porous media is between 0.98 and 1.62. With the increase of anisotropy factor, specific surface area of porous media increases by 0.33%-2.55% and the connected porosity decreases by 1.31%-2.00%. With the increase of Pcd, small pores in porous media increase and the specific surface area significantly increases (corresponding average specific surface area at three Pcd were 4.1×105 cm2/cm3, 4.7×105 cm2/cm3, 5.3×105 cm2/cm3 respectively). The connected porosity is less affected by Pcd and is negatively correlated with Pcd.
Fig. 5.
Fig. 5.
The relationship between specific surface area and anisotropy factor of anisotropic porous media.
Fig. 6.
Fig. 6.
The relationship between connected porosity and anisotropy factor of anisotropic porous media.
D3Q19 MRT-LB model was used to simulate fluid migration in 3D anisotropic porous media (parameters shown in Table 2). The deviation of simulation result is expressed as:
When the simulation deviation was less than 10-6, the simulation results were considered stable and the iteration process was ended.
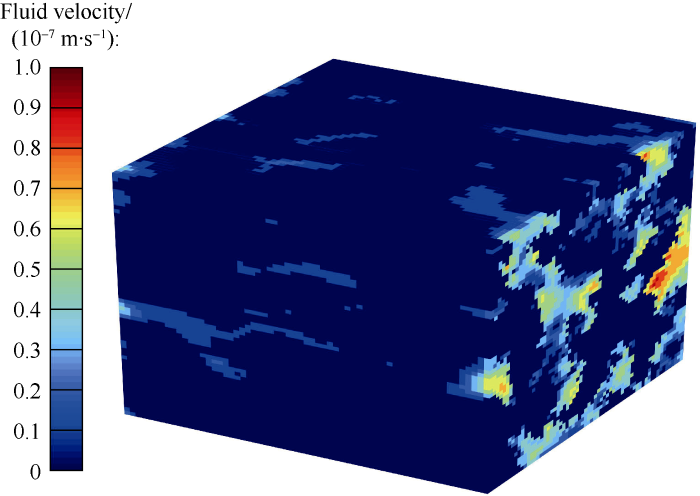
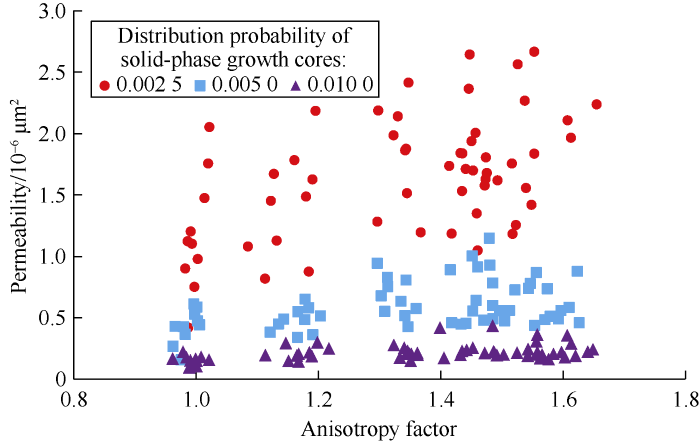
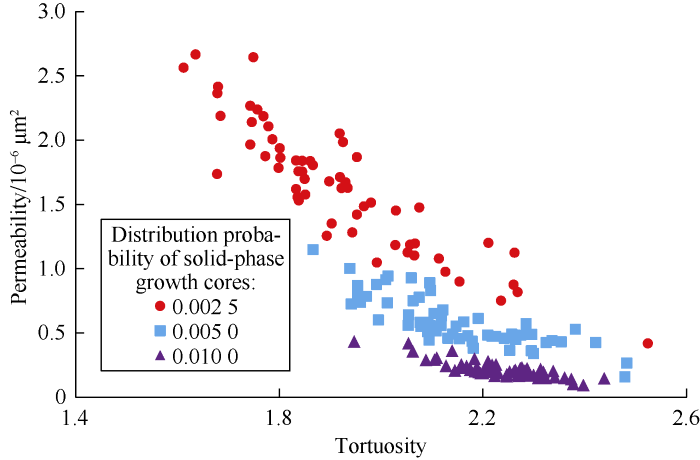
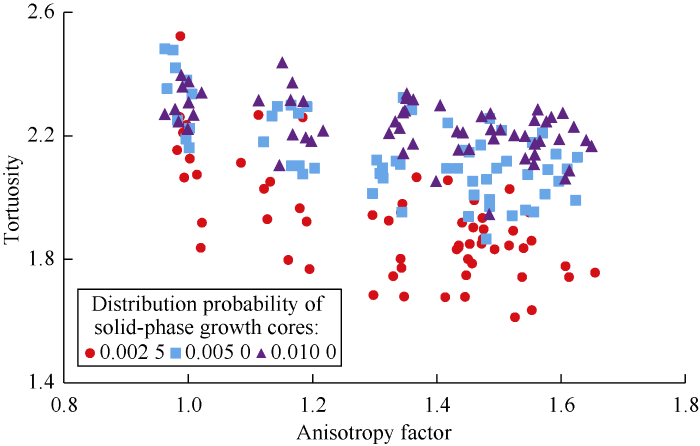
Fig. 7 shows the simulation result of anisotropic porous media with Pcd of 0.0025 and A of 1.55. Based on LBM simulation results on anisotropic porous media, equations (8) and (9) were used to calculate the permeability and tortuosity of 3D anisotropic porous media respectively to find out the relationships between permeability, anisotropy and tortuosity (Figs. 8-10). Figs. 8-10 show that the permeability of anisotropic porous media is positively correlated with anisotropy factor and is negatively correlated with tortuosity. The tortuosity is negatively correlated with anisotropy factor. As anisotropy factor increases from 0.98 to 1.62, the permeability of porous media with Pcd of 0.002 5, 0.005 0 and 0.010 0 increase by 80.20%, 60.97% and 57.38%, while the tortuosity decreases by 17.72%, 11.02% and 6.06% respectively.
Fig. 7.
Fig. 7.
Simulation result of 3D anisotropic porous media.
Fig. 8.
Fig. 8.
The relationship between permeability and anisotropy factor of anisotropic porous media.
Fig. 9.
Fig. 9.
The relationship between permeability and tortuosity of anisotropic porous media.
Fig. 10.
Fig. 10.
The relationship between tortuosity and anisotropy factor of anisotropic porous media.
It should be noted that: (1) The permeability of porous media obtained by digital core is closely related to the cell scale; as the cell scale increases by one order of magnitude, the permeability of porous media would increase by at least two orders of magnitude; (2) Since nanometer pores are abundant in the unconventional reservoirs, a small cell scale (10 nm) was selected in the simulation for better research on pore microstructure and its correlation with permeability; the perme-ability calculated by simulation results has a big difference from the measured results of actual rocks, but the correlation of permeability with pore microstructure has nothing to do with the cell scale.
2.3.2. Simulation of 3D heterogeneous porous media
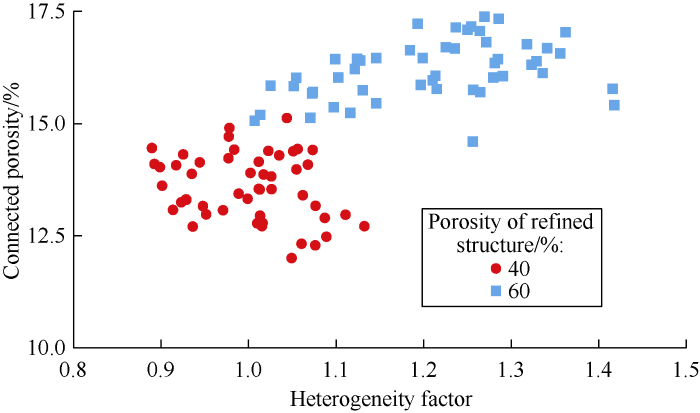
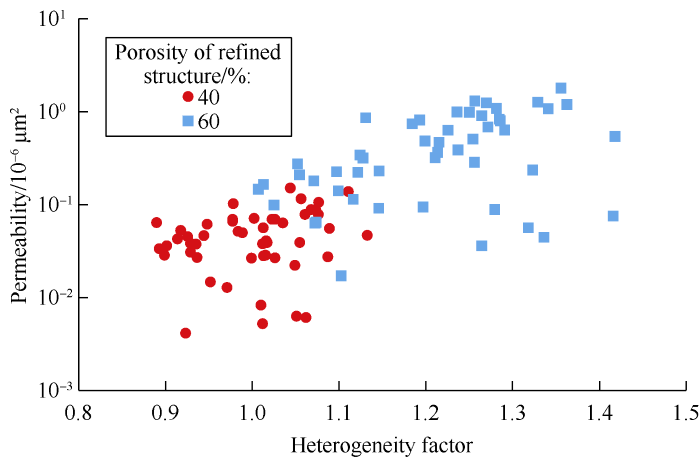
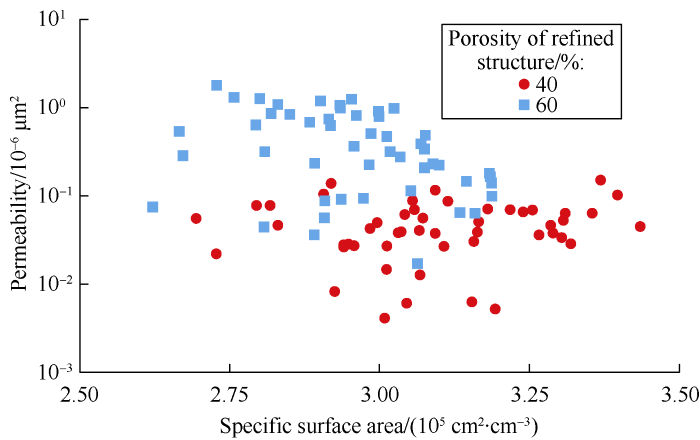
The QSGS algorithm was adopted to generate 3D heterogeneous porous media (detailed parameters shown in Table 3). The growth velocity of solid phase in the x, y and z directions were set same to exclude the influence of anisotropy. The grid number and cell scale were consistent with anisotropic porous media. In order to remove the effect of structure randomness, 10 random porous media models were constructed with the same group of parameters. A total of 100 models of heterogeneous porous media were generated. Then, the isolated pores were removed. The length, width and height of cell blocks were set at 16 lattices. The pore-distribution heterogeneity factor of porous media was calculated by equation (2) to find out the relationships of connected porosity and specific surface area with heterogeneity of 3D heterogeneous porous media respectively (Figs. 11 and 12). The figures show the calculated pore-distribution heterogeneity factors of porous media with different refined porosities have different ranges. When ϕR is 40%, the pore-distribution heterogeneity factor is from 0.89 to 1.13, while the heterogeneity factor is between 1.03 and 1.42 when ϕR of 60%. The connected porosity of porous media is weakly affected by heterogeneity, while specific surface area is negatively correlated with heterogeneity obviously. At ϕR of 40% and 60%, as heterogeneity factor increases, the connected porosity of porous media fluctuates less than 4.57%, but specific surface area decreases by 21.55% and 17.76% respectively.
Table 3 Basic parameters in QSGS algorithm.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pr | 0.01 | ϕ | 20% |
| Pc | 1×10-4, 8.5×10-5, 7×10-5, 4×10-5, 2×10-5 | D | 0.01 |
| ϕR | 40%, 60% |
Fig. 11.
Fig. 11.
The relationship between connected porosity and heterogeneity factor of heterogeneous porous media.
Fig. 12.
Fig. 12.
The relationship between specific surface area and heterogeneity factor of heterogeneous porous media.
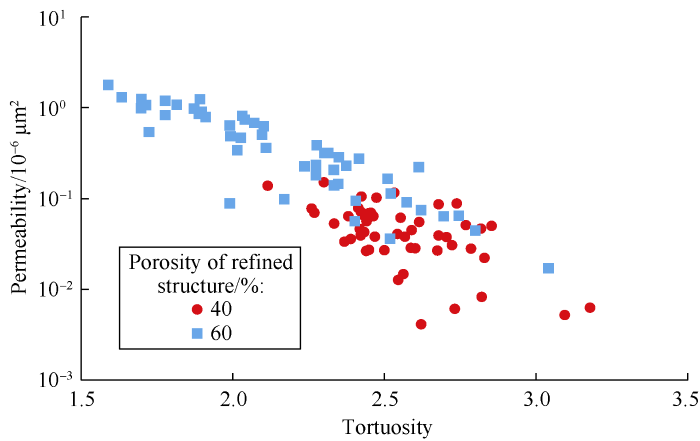
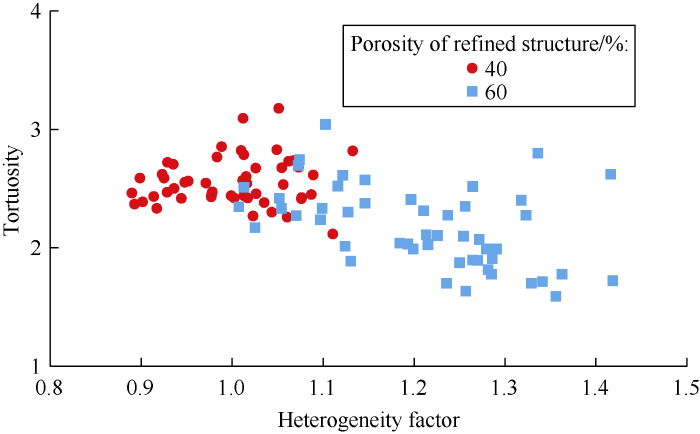
D3Q19 MRT-LB model was used to simulate fluid flow in heterogeneous porous media (parameters listed in Table 2). Based on simulation results, the permeability and tortuosity of 3D heterogeneous porous media were calculated by equations (8) and (9) respectively. The relationships between permeability, heterogeneity, specific surface area and tortuosity are shown in Figs. 13-16. It can be seen that the permeability of heterogeneous porous media is positively correlated with pore-distribution heterogeneity factor and refined structure porosity[26]. The greater the ϕR, the more the larger pores in the porous media and the greater the permeability. As heterogeneity increases, the permeability of porous media increases by 136.01% at ϕR of 40% and 344.53% at ϕR of 60%. Meanwhile, the permeability has no obvious correlation with specific surface area and is negatively correlated with tortuosity. However, there is no significant correlation between tortuosity and heterogeneity factor.
Fig. 13.
Fig. 13.
The relationship between permeability and heterogeneity factor of heterogeneous porous media.
Fig. 14.
Fig. 14.
The relationship between permeability and specific surface area of heterogeneous porous media.
Fig. 15.
Fig. 15.
The relationship between permeability and tortuosity of heterogeneous porous media.
Fig. 16.
Fig. 16.
The relationship between tortuosity and heterogeneity factor of heterogeneous porous media.
3. Analysis and discussion
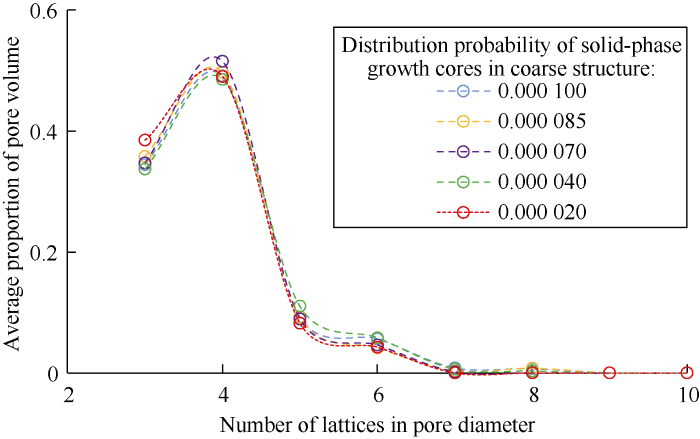
In the simulation of 3D anisotropic porous media, the magnitude of solid particles was cell scale[37], while the solid particle size increased gradually with distribution probability of coarse structure solid-phase growth core reducing in 3D heterogeneous porous media. The relationships between permeability, specific surface area, tortuosity and connected porosity and pore-scale anisotropy and heterogeneity were analyzed on this basis.The effects of pore anisotropy and pore-distribution heterogeneity on pore size and distribution of porous media were further studied to explore their influence mechanism on permeability of porous media. The maximum ball method was used to obtain pore diameter and the volume proportion of different pores in the pore space of 3D porous media. The main steps include: (1) Determining the correlation probability of the maximum ball radius; (2) Searching the maximum ball; (3) Deleting redundant balls (including single and multiple containment), etc. However, even if pore size and distribution in porous media are identical, different connecting relationships between pores will also cause change of permeability[1]. Therefore, 10 random porous media models were constructed for the same group of construction parameters.Because fluid migration in porous media occurs mainly in larger pores, the pores containing a single node weren’t considered when the maximum ball method was applied. Figs. 17 and 18 show the pore size distribution of anisotropic porous media at Pcd=0.0025 and heterogeneous porous media at ϕR=60% respectively. Where, the abscissa represents pore diameter and the ordinate represents the average volume proportion of 10 random porous media under the same group of construction parameters. According to Fig. 17, the pore size distribution of 3D anisotropic porous media is close at different growth velocities (corresponding to anisotropy) with the relative deviation from 1.78% to 8.64%. Fig. 18 shows that the pore size distribution of 3D heterogeneous porous media with different distribution probability of solid-phase growth core in coarse structure (corresponding to heterogeneity) are close to each other, with the relative deviation between 1.82% and 6.09%. Meanwhile, the relative deviation has nothing to do with the magnitude of anisotropy or heterogeneity.
Fig. 17.
Fig. 17.
Pore size distribution of anisotropic porous media.
Fig. 18.
Fig. 18.
Pore size distribution of heterogeneous porous media.
The relationships of pore structure parameters with anisotropy and heterogeneity are summarized (Table 4): (1) At the same value of Pcd, the connected porosity, pore size, specific surface area and solid particle size are hardly affected by anisotropy or have no obvious correlation with anisotropy in the 3D anisotropic porous media, while the tortuosity is obviously negatively correlated with anisotropy; (2) At the same value of ϕR, the connected porosity and pore size of porous media are less affected by heterogeneity in 3D heterogeneous porous media; although there is no obvious correlation between tortuosity and heterogeneity, tortuosity changes obviously; the heterogeneity of porous media is related to solid particles size, and specific surface area of porous media is negatively correlated with heterogeneity obviously.
Table 4 Relationships of pore structure parameters with anisotropy and heterogeneity.
| Pore structure parameter | Anisotropy | Heterogeneity |
|---|---|---|
| ϕeff | ϕeff slightly decrease as A increases | Small in variation |
| r | Variation is small and uncorrelated | Variation is small and uncorrelated |
| τ | τ decreases significantly as A increases | Variation is obvious and uncorrelated |
| S | S slightly increases as A increases | S decreases significantly as H increases |
| d | No variation and uncorrelated | d increases as H increases (associated with S) |
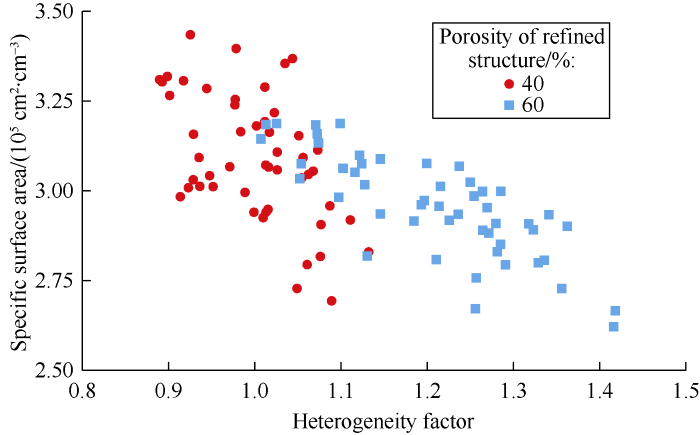
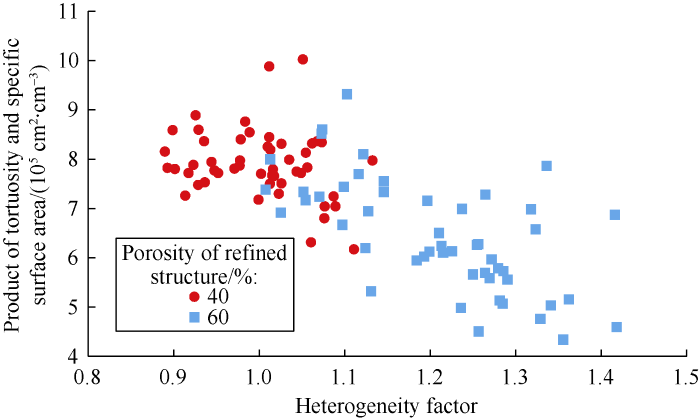
Pore-scale anisotropy and pore-distribution heterogeneity have significant effects on tortuosity and specific surface area of porous media respectively, and then influence the fluid flow dynamics: (1) As the anisotropy in the mainstream direction enhances, the orientation of long axis of pores is more likely to be along the mainstream direction[21], and the flow path is more straight, that means significant decrease of tortuosity. Consequently, the energy consumed when fluid flows through the porous media reduces and the permeability of the porous media increases. This demonstrates that strong correlation between tortuosity and anisotropy is the inherent reason why anisotropy influences permeability of porous media. (2) As pore-distribution heterogeneity increases, the larger the solid particles in the porous media, the more obvious the pore aggregation phenomenon will be[26], that means the chance of pores overlapping increase and obvious decrease of specific surface area. Generally, when porosity of porous media is similar, the larger the solid particles or the smaller the specific surface area of the porous media, the smaller the wall friction resistance the fluid will encounter when flowing through the porous media[38], and the larger the permeability of the porous media will be. (3) Although Fig. 14 shows that the permeability of 3D heterogeneous porous media has no obvious correlation with specific surface area, the permeability tends to increase with the increase of heterogeneity on the whole. This is because tortuosity is also an important factor influencing permeability of porous media[39]. Different from specific surface area and porosity, tortuosity is related to the direction and position of solid particles in porous media (especially the larger solid particles)[2]. In 3D heterogeneity porous media, solid particles become more different in size with the increase of heterogeneity. But the distribution location of solid particles is random, so tortuosity may increase or reduce. Therefore, there is no obvious correlation between tortuosity and heterogeneity. The effect of pore-distribution heterogeneity on permeability of porous media is mainly the combined effect of specific surface area and tortuosity. (4) Fig. 19 shows the relationship of the product of specific surface area and tortuosity with heterogeneity, which indicates that the product is obviously negatively correlated with heterogeneity. This demonstrates that the combined effect of specific surface area and tortuosity is the inherent reason of heterogeneity influencing permeability of porous media.
Fig. 19.
Fig. 19.
Relationship of the product of specific surface area and tortuosity with heterogeneity factor of heterogeneous porous media.
Based on simulation results, the permeability and tortuosity of 3D anisotropic, heterogeneous porous media (unsegmented φR) satisfy a power function relation (Table 5).
Table 5 The relations between permeability and tortuosity of 3D porous media.
| Porous media | Relation | Correlation coefficient square | |
|---|---|---|---|
| Anisotropic porous media | Pcd=0.002 5 | ${{K}_{0}}\text{=}0.014\ 6{{\tau }^{-3.46}}$ | 0.838 |
| Pcd=0.005 0 | ${{K}_{0}}\text{=}0.016\ 4{{\tau }^{-4.44}}$ | 0.681 | |
| Pcd=0.010 0 | ${{K}_{0}}\text{=}0.020\ 7{{\tau }^{-5.74}}$ | 0.695 | |
| Heterogeneous porous media | ${{K}_{0}}\text{=}0.120\ 8{{\tau }^{-8.24}}$ | 0.749 | |
The coefficients a and b are related to pore structure of porous media. b is negatively correlated with pore size of porous media and positively correlated with specific surface area. The simulation results show the correlation coefficient square is nearly 70%, and up to 80%, indicating that equation (11) can estimate core permeability accurately.
In conclusion, the permeability model that characterizes unconventional reservoirs must include the two parameters, pore-scale anisotropy and pore-distribution heterogeneity, to better reflect the influence of microscopic pore structure on fluid flow[15].
4. Conclusions
The pore morphology of tight sandstones is complex. The pore anisotropy and pore-distribution heterogeneity are strong, while the anisotropy factor in the mainstream direction is the greatest and in the other directions are approximate.
The anisotropy affects the orientation of long axis of pores and fluid flow path in porous media. Along the direction with the greater anisotropy factor, tortuosity and energy dissipation is less. The strong correlation of tortuosity with anisotropy is the inherent reason of anisotropy influencing permeability of porous media.
The effect of pore-distribution heterogeneity on permeability of porous media is the combined effect of specific surface area and tortuosity. The product of specific surface area and tortuosity is obviously negatively correlated with heterogeneity. As pore-distribution heterogeneity is stronger, the product is less and the permeability of porous media is greater.
The permeability and tortuosity of complex porous media satisfy a power relation with a high fitting precision, which can be applied for approximate estimation of core permeability.
Nomenclature
a—fitting coefficient, 10-3 μm2;
A—anisotropy factor, dimensionless;
b—fitting coefficient, dimensionless;
cs—sound speed, m/s;
Cs—solid-phase growth core;
d—solid particle size, m;
D—growth velocity of solid phase, f;
Dx, Dy, Dz—growth velocity of solid phase in the x, y, z direction, f;
ei—lattice velocity, m/s;
fi(x, t), fj—discrete distribution function, kg/m3;
feq,j—equilibrium distribution function, kg/m3;
g—sequence number of pores or cell blocks;
H—pore-distribution heterogeneity factor, dimensionless;
hg—height of the gth pore, m;
i, j—discrete velocity direction;
k—growth direction of solid phase in QSGS algorithm;
K0—permeability, 10-3 μm2;
M—transformation matrix;
M-1—inverse matrix of M;
n—number of cell blocks divided in porous media;
nx, ny—average pore number encountered by a line per unit length as the line across the porous media in the x or y direction;
N—total number of pores in porous media;
o, p, q—coordinates in the x, y and z direction of porous media;
Pc—distribution probability of solid-phase growth cores in coarse structure, f;
Pcd—distribution probability of solid-phase growth cores, f;
Pk—growth velocity in different directions, f;
Pr—distribution probability of solid-phase growth cores in refined structure, f;
r—lattices number contained in pore radius;
Re—Reynolds number, dimensionless;
se, sm, sq, sv, sε, sπ—relaxation rates of energy moment, third-order moment, energy flux moment, stress tensor moment, energy square moment, quartic order moment, dimensionless;
S—specific surface area, cm2/cm3;
S—diagonal matrix;
t—time, s;
u—fluid velocity, m/s;
u(o, p, q)—fluid velocity of point (o, p, q) in porous media, m/s;
u(o, p, q, t)—fluid velocity of point (o, p, q) in porous media at the time t, m/s;
ux(o, p, q)—fluid velocity of point (o, p, q) in x direction, m/s;
$\overline{u}_{x}$ —average fluid velocity in the x direction, m/s;
wg—width of the gth pore, m;
wi—weight coefficient, dimensionless;
x, y, z—three directions in the space rectangular coordinate;
δt—time step, s;
δE—relative deviation of simulation results, dimensionless;
δL—cell scale, m;
p—pressure gradient, Pa/m;
μ—dynamic viscosity, Pa•s;
v—kinematic viscosity, m2/s;
ρ—fluid density, kg/m3;
τ—tortuosity, dimensionless;
τR—dimensional relaxation time;
ϕ—porosity of porous media, %;
Reference
Permeability in multi-sized structures of random packed porous media using three-dimensional lattice Boltzmann method
Analytical derivation of tortuosity and permeability of monosized spheres: A volume averaging approach
.DOI:10.1103/PhysRevE.83.026312 URL [Cited within: 2]
A new fractal permeability model for porous media based on Kozeny-Carman equation
Ueber kapillare leitung des wassers im Boden, Sitzungsber
.
Fluid flow through granular beds
The effect of rate of flow on rate of dyeing Ⅱ: The mechanism of fluid flow through textiles and its significance in dyeing
Influence of porosity and particle size distribution in resistance of porous flow
DOI:10.1002/cite.330430106 URL [Cited within: 1]
Variation of permeability with porosity in sandstone diagenesis interpreted with a fractal pore space model
Permeability- porosity relationship in RTM for different fiberglass and natural reinforcements
DOI:10.1177/0021998304039269 URL [Cited within: 1]
Modeling of Darcy-Forchheimer drag for fluid flow across a bank of circular cylinders
Permeability and effective porosity of porous media
DOI:10.1103/PhysRevE.56.3319 URL [Cited within: 1]
Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: Results for the permeability and drag force
DOI:10.1017/S0022112004003295 URL [Cited within: 1]
Advanced study about the permeability for micro-porous structures using the Lattice Boltzmann method
DOI:10.1007/s11242-009-9438-6 URL [Cited within: 1]
A new method for predicting permeability based on modified Kozeny-Carmen equation
Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance
DOI:10.1038/aps.2011.203 [Cited within: 1]
Micro pore and throat characteristics and origin of tight sandstone reservoirs: A case study of the Triassic Chang 6 and Chang 8 members in Longdong area, Ordos Basin, NW China
Insight into the pore structure of tight gas sandstones: A case study in the Ordos Basin, NW China
China’s shale gas exploration and development: Understanding and practice
Model construction of micro-pores in shale: A case study of Silurian Longmaxi Formation shale in Dianqianbei area, SW China
Multiscale simulation and analysis for gas flow in deep-seated micronano pore
Anisotropy and stress dependence of permeability in the Barnett shale
DOI:10.1007/s11242-015-0482-0 URL [Cited within: 2]
Shale permeability measurements on plugs and crushed samples
A review on pore structure characterization in tight sandstones
DOI:10.1016/j.earscirev.2017.12.003 URL [Cited within: 1]
Three dimensional characterization and quantitative connectivity analysis of micro/nano pore space
DOI:10.1016/S1876-3804(16)30057-X URL [Cited within: 1]
Pore-scale geometry effects on gas permeability in shale
DOI:10.1016/j.jngse.2016.07.057 URL [Cited within: 8]
Validity of the permeability Carman-Kozeny equation: A volume averaging approach
Pores in Marcellus shale: A neutron scattering and FIB-SEM study
An Enskog based Monte Carlo method for high Knudsen number non-ideal gas flows
The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: A review
Determining the impact of rectangular grain aspect ratio on tortuosity- porosity correlations of two-dimensional stochastically generated porous media
DOI:10.1007/s11434-016-1020-3 URL [Cited within: 1]
Simulation of gas flow in micro-porous media with the regularized lattice Boltzmann method
DOI:10.1016/j.fuel.2017.05.080 URL [Cited within: 1]
Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. A
DOI:10.1098/rsta.2001.0955 URL [Cited within: 1]
An evaluation of lattice Boltzmann schemes for porous medium flow simulation
Calculation of the permeability in porous media using the lattice Boltzmann method
Slow flow through a periodic array of spheres
DOI:10.1016/0301-9322(82)90047-7 URL [Cited within: 1]
A computing method of shale permeability based on pore structures
Gas-solid drag coefficient for ordered arrays of monodisperse microspheres in slip flow regime
Influences of fractal characteristics of reservoir rocks on permeability