To solve the problem that it’s difficult for two-point geostatistics modeling to reproduce geological bodies with complicated morphologies, Guardiano and Srivastava proposed multiple-point geostatistics in 1993^[1], in which training images are scanned through data templates to acquire data events and reflect corresponding geological models. Occurrence frequencies of different data events are approximated to multiple- point combined distribution probability in the space. The idea of multiple-point geostatistics is to establish training images through sedimentological analysis by using limited geological data, and sort out the optimal data event in the training images under the constraints of conditional data as the basis for sampling of the points to be simulated. As multiple-point geostatistics algorithm itself is already mature at present^[2,3,4,5,6], training image is deemed one of key factors deciding implementation effect of simulation^[7,8,9,10]. In order to acquire reasonable training images, researchers have proposed different methods such as target-based method^[11,12,13], sedimentation process-based method^[14,15], pseudo-sedimentation process-based method^[16,17], and geological data conversion-based method^[18,19], etc. The same parameter combination can be used to create a large number of different training images approximate to the underground geological conditions with the abovementioned methods. Even though these training images are very similar, they are different somehow in adaptability with the geological body to be simulated. Therefore, it’s very important to select the training image suitable for the simulation target best, which has attracted extensive attention^{[8-9, 20-21]}.

So far, algorithms dedicated for selection of training images mainly include three kinds, variogram-based selection methods, conditional probability-based selection methods^{[8-9, 20]} and similarity distance-based selection methods^[21]. Variogram- based selection method can only compare second-order spatial structural characteristics but can’t realize quantitative analysis of higher-order geostatistics characteristics^[21]. Ortiz and Deutsch proposed a sequencing method of training images using high-order geostatistics information^[20]. Boisvert suggested an selection method of training images based on data event distribution and multiple-point conditional probability equation^[8]. However, the two methods only extract 1D data events along well trajectory for analysis without consideration of complexity of higher-order data events under multi-well conditions, so they can’t effectively acquire high-order geostatistics information at different positions in 3D space or satisfy the demand of multi-well combined high-order data event analysis in the selection of training images. Pérez put forward a selection method of training images based on high-order compatibility of data events^[9]. This method groups the data events with the same number of condition points into one type, calculate the compatibility of the data event in the training image, and then optimize training image. But this method lays too much emphasis on unification of quantity of known points in the data event extraction process, resulting in different 3D structures of extracted data events, so the true matching degree between training images and conditional data can’t be revealed. Feng proposed a selection method based on similarity calculation and ranking of data events^[21]. This method calculates similarity between data event corresponding to each grid node in the simulation network and data event with the same spatial structure in training image, and select training image through mean value and variance of similarity attribute body. Emphasizing matching degree of spatial structure of data events, the method acquires limited data events for similarity calculation when a small number of conditional points are available, and thus reduces in reliability of selected result. Meanwhile, this method needs to scan training images for multiple times to calculate similarity between data events, making the selection take too much time.

Based on studies of predecessors, an improved selection method is presented in this paper based on the selection method with high-order compatibility proposed by Pérez, namely statistical method of repetition probability of data events, including unmatching ratio of data events and variance of their repetition probabilities. The lower the unmatching ratio of data events, and the smaller the variance of repetition probabilities, the higher the matching degree between training image and the study area will be. The test of theoretical model and actual model shows that this method can rank and select training images very well. This study provides a new means of selecting training images for multiple-point geostatistics modeling and can better serve multiple-point geostatistics modeling.

The selection method with high-order compatibility proposed by Pérez scans training images through data templates to acquire repetition times R_i,j of a data event and relative frequency P_i,j of repetition times in each training image^[9], conducts normalization treatment of relative frequencies of data events in each training image and then obtains relative compatibility C_j of each training image, where relative frequency P_i,j refers to proportion occupied by times of repetition of the ith data event in the jth training image in the total times of repetition of this data event in t training images, namely:

Relative compatibility C_j refers to the proportion of total relative frequencies of n data events in the jth training image to the total sum of relative frequencies of n data events in t training images, namely:

Absolute compatibility M_j refers to whether the ith data event appears in the jth training image, if it does, Y_i,j is 1, otherwise it is 0. Percentage of data evens contained in this training image is calculated:

This method deems that the higher the compatibility, the higher the matching degree of training images. However, as it only considers quantity of conditional data points but doesn’t consider spatial distribution differences of different data points, errors will appear in the compatibility statistics between training images and real data events, and training images can’t be selected accurately.

Repetition probability of a data event aims at reflecting distribution features of the specific data event in training image. Conditional data is scanned using the designated template to obtain the set CE of n data events in the alternative training image, and times of occurrence of the ith data event CE_i in the jth training image is searched and recorded as R_i,j. Distribution features of data events in each training image are calculated, namely variance σ_j of repetition probabilities of data events and unmatching ratio UNP_j of data events (hereinafter abbreviated as variance of repetition probability and unmatching ratio).

The proportion of repetition times R_i,j of a single data event in repetition times of all data events in the training image is named repetition probability of a data event, namely:

Variance σ_j of repetition probability is variance of repetition probabilities of data events in the training image, namely:

where $\overline{P{{T}_{j}}}$is mean value of repetition probabilities of data events in the jth training image.

If a matching data event is searched out in the training image, then indicator value U_i,j is recorded as 1, otherwise is 0. Proportion of unmatching data events is calculated, namely unmatching ratio UNP_j of data events:

Low unmatching ratio indicates that geological models matching the actual area are abundant in the training image. If variance of repetition probabilities is small, then geological models matching the actual area are stable in distribution in the training image. Therefore, a better training image has lower unmatching ratio and smaller variance of repetition probabilities.

A proper searching template is selected for the established network model of the study area. Conditional data event is used to scan training images to obtain models completely match. Repetition time of the data event increases until the searching of all data events is completed. Returning to repetition times R_i,j which completely match the conditional data event, repetition probability PT_i,j of data events is calculated. According to repetition probability PT_i,j of data events, variance σ_j of repetition probabilities and unmatching ratio UNP_j are calculated, which are then used to select training images. The specific steps are as follows: (1) Determine the searching template and seek for data events; (2) Select a data event, scan training images and seek for models matching the data event. If conditional point of the data event is completely matched in the training image, the repetition times R_i,j of this data event increases by 1, until the searching of this training image is completed; (3) Turn to the next data event and repeat step (2) until all data events are finished searching; (4) Select the next training image and repeat steps (2) and (3) until all training images are scanned; (5) Calculate repetition probability of data events, PT_i,j; (6) Calculate variance σ_j of repetition probability and unmatching ratio UNP_j to complete selection and ranking of training images.

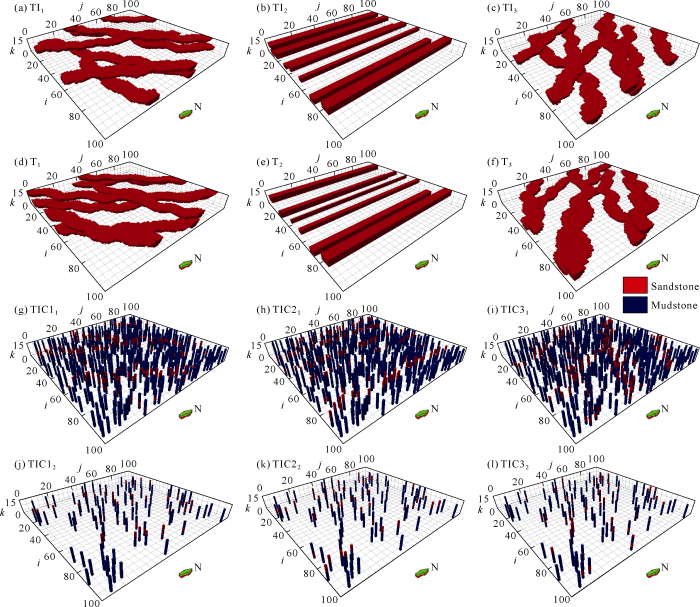
3D test grids were 100×100×15, and each grid was 10 m×10 m×0.5 m, 3 phase models TI₁, TI₂ and TI₃ with different specifications were established (Fig. 1a-1c), conditional data TIC1₁, TIC2₁ and TIC3₁ acquired by 500 wells were randomly generated (Fig. 1g-1i), and percentage of conditional points was 5%. Of the three phase models, TI₁ and TI₃ were both fluvial facies models and only different in provenance direction, TI₂ was a simple strip model without obvious gradual change features in vertical direction. Three training images T₁, T₂ and T₃ (Fig. 1d-1f) were established corresponding to the 3 models. It was expected that training images approximate to the prototypes be selected according to their respective conditional data.

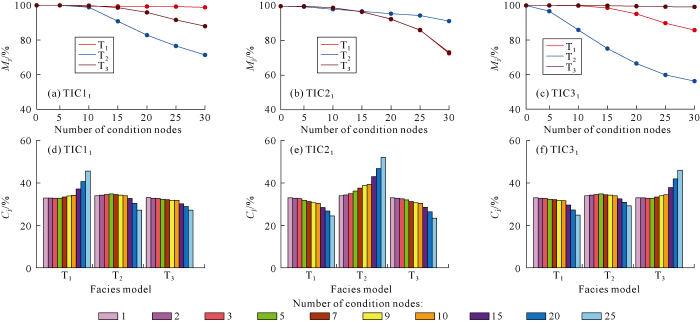
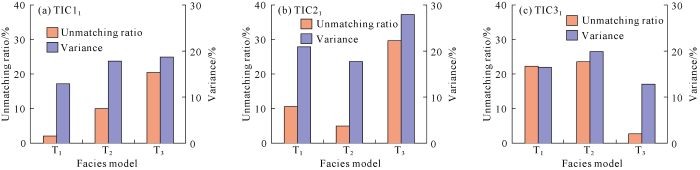
For conditional data in each group, high-order compatibility method and statistical method of repetition probabilities of data events were used to screen training images respectively. The searching template 7×7×5 was set. According to the high-compatibility method, repetition times of data events were calculated when 1, 2, 3, 5, 7, 9, 10, 15, 20 and 25 conditional points were searched to obtain corresponding absolute compatibility (Fig. 2a-2c) and relative compatibility (Fig. 2d-2f). The improved method was used to calculate unmatching ratio and variance of repetition probability for data events satisfying 15 conditional points (Fig. 3). Test results show that selection results of both methods meet expectations, so they can be used to select training images.

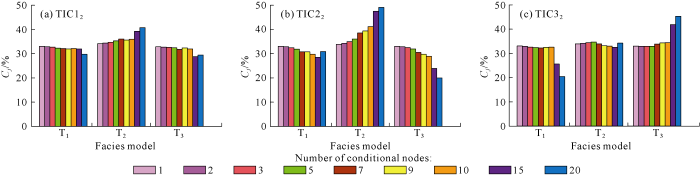
Conditional data points in an actual oil reservoir are quite few relative to grid data in the study area, so percentage of conditional data was reduced to 1% based on the original test model (Fig. 1j-1l). Under scarce conditional data, effect and applicability of the two methods were evaluated. The results show that high-order compatibility method can’t effectively select matching training image after rarefying (Fig. 4). In the selection, training image T₂ was selected at conditional point TIC1₂, which goes against the expected result (Fig. 4a). Conditional point TIC3₂ could be obviously distinguished only when number of conditional points was greater than 15. In comparison, the new method can still select the training image effectively when data events satisfying 9 conditional points were counted (Fig. 5). Obviously, the improved method has a leading edge, and can be used to select training images for the actual oil reservoir.

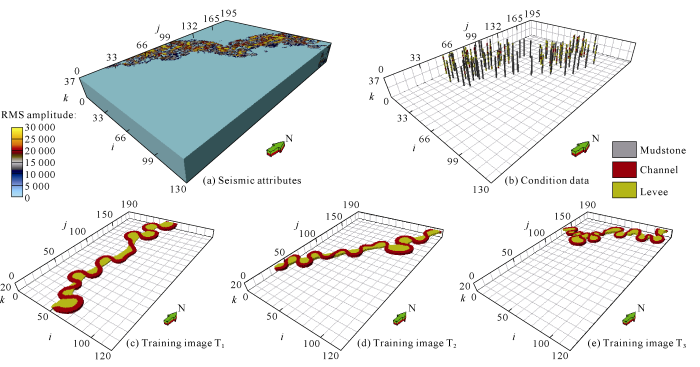
Angola Plutonio Oilfield is located in the south end of West Africa Lower Congo-Congo fan basin and middle-lower part of the present continental slope, with a water depth of 1000-1500 m. The main oil-bearing layer is Tertiary Oligocene O73 sand group. Previous studies show that O73 sand group in this area is typical deep-water turbidite channel sediment^[22]. This area mainly has channel and natural levee microfacies, in which the channel sandstone is the main reservoir rock. This area experienced intense tectonic deformation, and affected by salt diapirism in the late stage, sand bodies are complicated in structure. The stratum studied this time is a shallow stratum of turbidite channel sand deposit, stable in structure, intact in morphology and high in seismic data resolution. Channels at shallow stratum and deep stratum have similar sedimentary environment, so shallow-stratum high-resolution seismic data was used to extract channel morphological parameters to guide establishment of training images. Stratal slicing was conducted according to shallow- stratum seismic RMS (Root Mean Square) amplitude property and turbidite channel was quantitatively interpreted by combining logging information in the working area. It’s speculated that the turbidite channel was 850-2 500 m wide, in which sand bodies were 8-23 m thick and 91-305 m wide. Turbidite channels in small layers of the target formation interval in the study area have different directions. According to multiple parameters like width, thickness, curvature, and flow direction, etc., the improved Alluvsim algorithm^[23] was used to establish 3 training images approximate to the turbidite channels at the target stratum. The grids were 120×190× 20 in number (Fig. 6) and 20 m×20 m×0.75 m each in size.

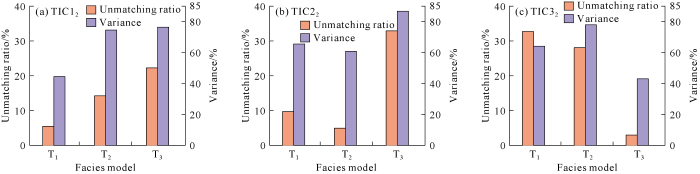
Turbidite channels in the small layers at the target interval were modeled (Fig. 6a). The grid model of the study area was 130×195×37 in grid number and 20 m×20 m×0.75 m in grid size. The new method presented in this paper was used to select training images. The searching template was set at 11×11×3, repetition probability of the data events satisfying 6 conditional points were counted, and variance of repetition probability and unmatching ratio were obtained (Fig. 7). The training image T₂ has the lowest variance of repetition probability of data event and unmatching ratio, indicating that it is the optimal training image.

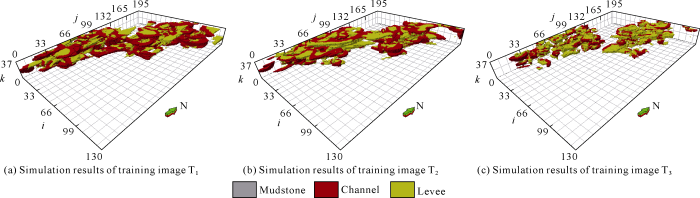
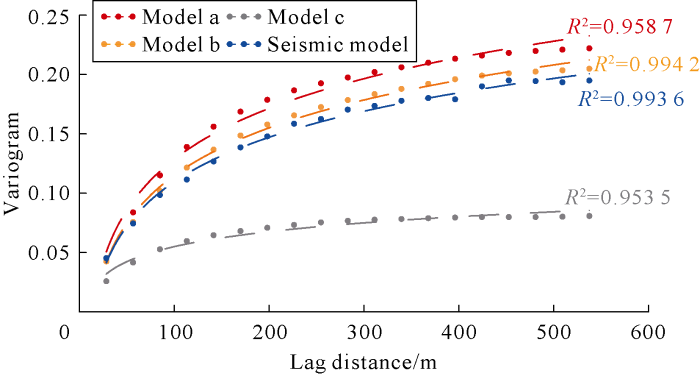
Multiple-point geostatistics SNESIM method^[24] was used for modeling with the same parameters to acquire geological models generated by the three training images (Fig. 8). Variograms of the 3 geological models were calculated and compared with variogram of the actual seismic attribute body (Fig. 9). Variogram of model a has the greatest difference from the actual seismic variogram, followed by model c, while variogram of model b is the most approximate to variogram of seismic attribute body, indicating that petrofacies continuity of model b is close to the continuity of seismic attribute, namely simulation result of training image T₂ accords with the actual geological features better, and this is consistent with the selection result. The improved method works well in selecting training images for actual oil reservoirs and multiple-point geosta-tistics modeling.

Repetition probability of data events, which starts from spatial differences of data events, takes stability of data events as the index for selection of training images. By evaluating model stability with variance of repetition probability and evaluating model diversity with unmatching ratio, this method can select training images more comprehensively. A better training image has stable sedimentary model distribution. The smaller the variance of repetition probability, the higher the stability of geological models in the corresponding training image is; the lower the unmatching ratio, the higher the completeness of geological models in the corresponding training image is.

Theoretical model test shows that with few conditional data points, the index of repetition probability of data events can effectively sort out the optimal training image. In the Angola Plutonio Oilfield test in West Africa, multiple training images were established according to morphological characteristics of turbidite channels extracted according to shallow-stratum high-resolution seismic data in the study area. This method can effectively select the training image having the highest matching degree with the target stratum. The geological model established using the selected training image has good correspondence with seismic attribute, thus enhancing accuracy of multiple-point geostatistics modeling.

C_j—relative compatibility of the jth training image;

M_j—absolute compatibility of the jth training image;

n—total number of conditional data events;

P_i,j—relative frequency of repetition times of a data event in each training image;

PT_i,j—repetition probability of the ith data event in the jth training image;

$\overline{P{{T}_{j}}}$—mean value of repetition probabilities of data events in the jth training image;

R—multiple correlation coefficient;

R_i,j—repetition times of the ith data event in the jth training image;

t—quantity of training images participating in the selection;

UNP_j—unmatching ratio of a data event in the jth training image;

U_i,j—indicator value for the ith data event to be matched in the jth training image;

Y_i,j—indicator value for the ith data event appearing in the jth training image;

σ_j—variance of repetition probability of data events in the jth training image.