Introduction
Study of fluid flow through porous rocks is important for solving environmental and energy problems[1,2]. In a geological model that contains many cells, the solution of fluid flow equations is not be possible with respect to the volume of calculations at the fine scale. The process of increasing the scale due to converting a fine scale model into a coarse scale model with the idea of maintaining important information on reservoir properties is called upscaling[3,4]. The upscaling method can decrease the calculation and computation time[5,6,7,8,9,10].
Many scholars have worked to improve the upscaling methods, and they have achieved very good results, but there are limitations and problems in the process of the property upscaling[11,12,13,14,15,16,17,18]. Traditional upscaling methods are based on the averaging[19,20,21], and they are not applicable to the cases with strong heterogeneity. Laplacian-with-skin method is used to conduct stochastic analysis on three-dimensional hydraulic conductivity upscaling results[17], and the multiple boundary method is used for upscaling permeability of three-dimen-sional fractured porous rocks[17,18]. In wavelet-based upscaling method, the selection of threshold is highly required[22,23,24]. Based on the traditional concept of threshold functions which are divided into hard and soft threshold functions[25], Ge et al. (2015) developed a hybrid threshold function to avoid drawbacks of hard and soft threshold functions[26,27]. So far, most of upscaling methods have only pointed to upscaling of one reservoir property in one dimension or more dimensions and none of them can realize the simultaneous upscaling of two or more reservoir properties. In this paper, we use adaptive bandwidth technique in the kernel function method to upscale two reservoir properties simultaneously in one dimension. Considering that in the primary model, upscaling is related to the cell variability, the variable bandwidth approach is adopted and the bandwidth in the kernel function method is considered as the degree of system variability. Methods for determination of variable bandwidth include: (1) In dynamic or adaptive bandwidth, by setting the threshold, upscaling of each cell can be attributed to the cell variability. (2) The threshold is limited to the desired number of bands or blocks with the use of error values. In the wavelet transformation, upscaling is carried out in binary format, and in the whole process, there is no idea about the number of upscaled blocks. The previous studies are not capable of determining the number of blocks from the very beginning of the upscaling process. The kernel-based upscaling approach proposed in this paper can determine the number of upscaled blocks of the model from the beginning of the upscaling process.
In the present study, the upscaling algorithm based on the adaptive bandwidth in the kernel function method is first investigated from theoretical point of view, and then, the results of the upscaling of each feature are displayed separately. Finally, an identical model with the same upscaled blocks number is presented for simultaneous upscaling of two properties using two different approaches.
1. Methodology
The main idea in the kernel function method is to estimate the distribution function at a point (such as x) using neighborhood observations. The kernel function method is a flexible method for estimating the distribution density of specified data. The kernel function is structurally similar to the histogram, but its main fundamental difference from the histogram is that, in the kernel, the density calculation is based on the specified distance around the value of x and with different weights, whereas in the histogram, the density is calculated at a distance including the value x and its center with the same weights depends on each neighborhood. Assume that X1, X2, …, Xn are random samples of population n. If the sample result is shown with x1, x2, …, xn, the distribution function estimated using the kernel function can be expressed as follows[28]:
Kernel functions are usually probability density functions, i.e. they integrate to one, and x in the domain of K satisfies $K\left( x \right)\ge 0$. An immediate consequence of $\int{K\left( x \right)}\text{d}x=1$ is $\int{{{{\hat{f}}}_{h}}\left( x \right)}\text{d}x=1$, and the kernel density estimator is also a probability density function. The two main parameters of each kernel function include the type of kernel function and the kernel bandwidth. When the kernel function method is used for density function estimation, the kernel function itself has little effect but the proper choice of bandwidth h is of great importance[29]. Given that the upscaling of the system is related to the cell variability, the bandwidth in kernel estimator can be considered as a function of the degree of system variability. In areas with extreme variability and plenty of information, any method for upscaling regardless of the accuracy and mode of operation, should try to maintain the main features of the system, short-range bandwidth can obtain the goal of upscaling, and we can see the smallest upscaling degree. Therefore, these areas will be remained in fine scale. Conversely, in areas with low or smooth variation, with a sufficiently large bandwidth selection, the largest number of primary cells will be merged and the fine scale will become coarse scale.
Variable bandwidth can directly indicate the degree of system variability. The dynamic method is used to determine the optimal bandwidth. Assuming that the random samples are x1, x2, …, xn, estimation of the density function using the kernel function method with variable bandwidth is given by the following equation:
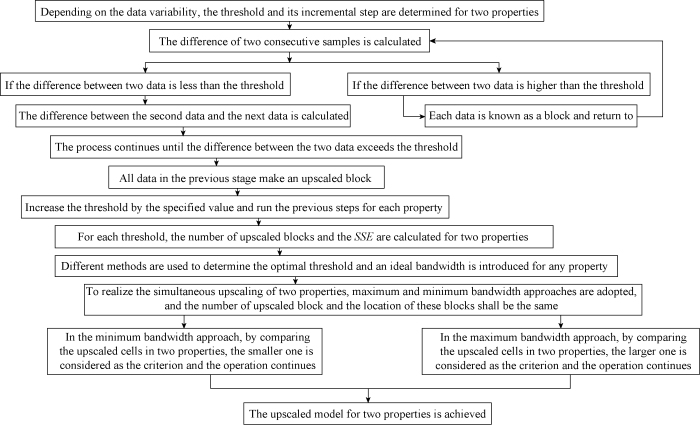
The threshold or bandwidth defined in this problem is controllable so that the amounts of change as well as its maximum changes are obtained from the data. Upscaling steps of two properties based on the adaptive bandwidth of the kernel function are shown in Fig. 1. The main difference between this method and conventional upscaling methods is that the coarsening of the cells in this method is based precisely on the inherent variability of the property. By determining the variable bandwidth, in some areas where the variability is high, the bandwidth will be small and cells will remain as small as possible. Conversely, in areas with a small change in reservoir characteristics, large bandwidths are considered and more cells are upscaled. This has a great deal about the multiresolution nature of the kernel bandwidth method.
Fig. 1.
Fig. 1.
Flowchart of simultaneous upscaling of two properties in one dimension using the adaptive bandwidth in the kernel function method.
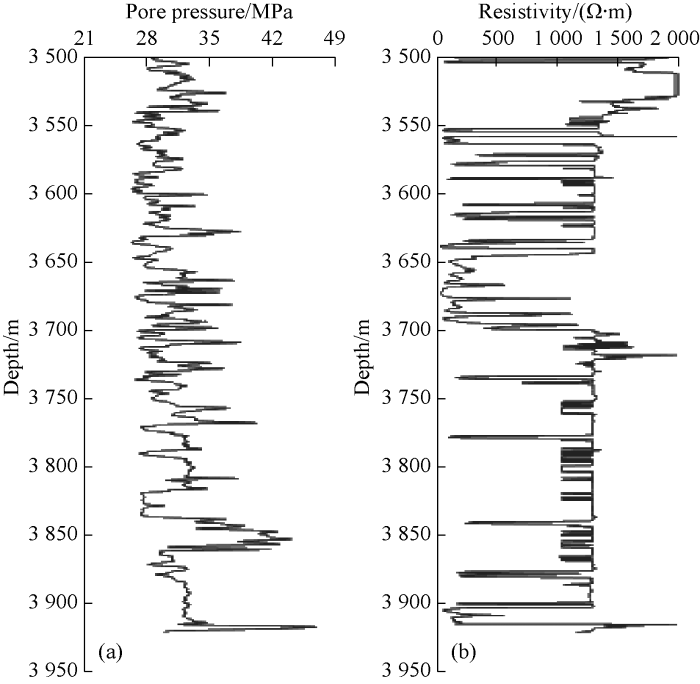
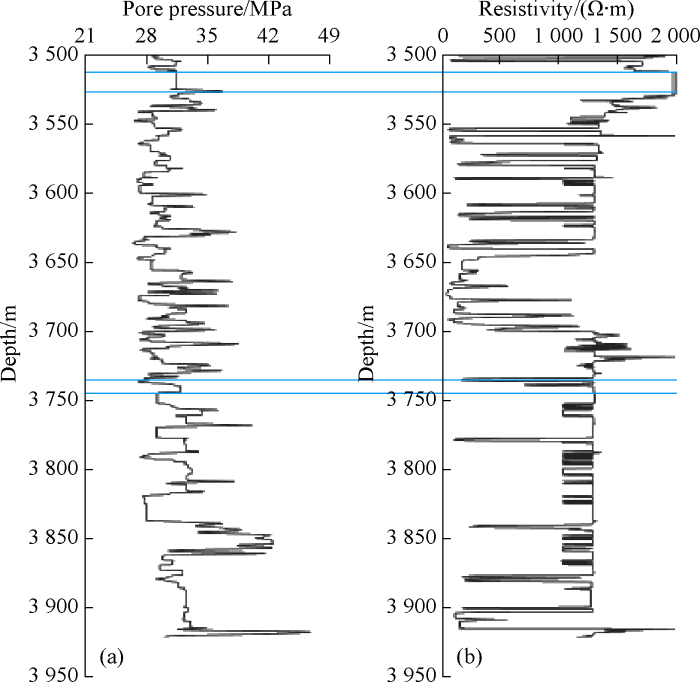
The proposed method is applicable to any type of log data, including radioactivities, electrical, sonic or mechanical logs. In this paper, pore pressure and resistivity logs are taken as the examples for upscaling, and these two features are two different data sets which are measured in the well. Pore pressure and resistivity are measured at 2413 samples along the well depth of 450 m (Fig. 2). The maximum threshold and the variation of threshold are obtained based on the difference between the maximum value and the minimum value.
Fig. 2.
Fig. 2.
(a) Pore pressure log and (b) resistivity log.
2. Upscaling results
2.1. One-dimensional upscaling of each property
In upscaling with the adaptive bandwidth method of the kernel function estimator, if the variability of two adjacent cells is less than the threshold or bandwidth, the cells can be converted to a larger block. Upscaling is heavily dependent on the threshold value. If lower thresholds are selected, less number of cells will be scaled up, while by choosing a higher threshold, the number of cells to be upscaled will increase, and ultimately, the number of blocks will heavily decrease.
In kernel function bandwidth-based upscaling, the computational efficiency can be controlled by defining thresholds. In this proposed method, the threshold can be calculated as a function of the number of needed cells, and the number of cells is a function of time. By changing the threshold, the error value and the number of blocks will change. The higher number of cells will increase the computation time, and subsequently will increase the accuracy. In contrast, as the sizes of the cells increases, the computation time will decrease and the accuracy will also decrease. The main idea of using the kernel bandwidth is to run a simulator at a reasonable time with the highest accuracy. Increasing the accuracy requires an increase in the number of cells, thus when the sizes or dimensions of the cells are kept small, what is happening on the other side is that the large number of cells will greatly increase computation volume and decrease computational efficiency. The computational efficiency depends entirely on the number of cells. If the number of cells is fixed, for example, if n cells are needed and the time to perform computations is t, then, in the simulation process, it becomes n cells when the multi-resolution upscaling is performed based on variability. Then the model is executed so that the number of cells controls the maximal variance of the primary model, and finally, the resulting model will have acceptable accuracy. In this regard, the number of upscaled blocks can be controlled by considering the kernel evaluation criteria such as mean square error (MSE), cumulative or sum of square error (SSE), and the defined threshold, In the kernel upscaling method, the variability of the considered reservoir feature is a function of the threshold and by controlling this threshold, the number of final blocks of the model is determined. This is the main difference between the kernel and the wavelet transformation upscaling methods.
In the proposed algorithm, the variable bandwidth value varies from 0 to the maximum value, which can be equal to the difference between the minimum and the maximum of the data. For each arbitrary bandwidth, the data x1, x2, …, xn are assumed to located in the bandwidth range. If the mean of these data is equal to$\bar{x}$, SSE can be obtained from the following equation:
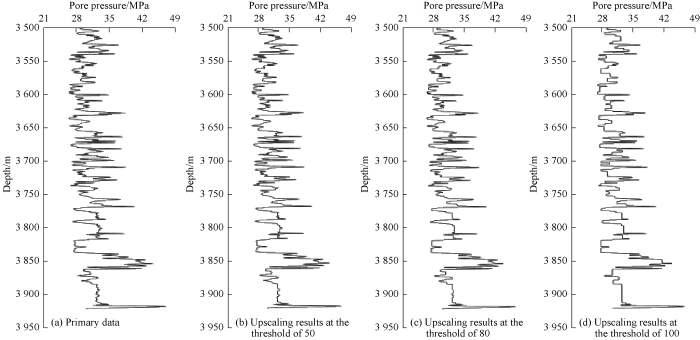
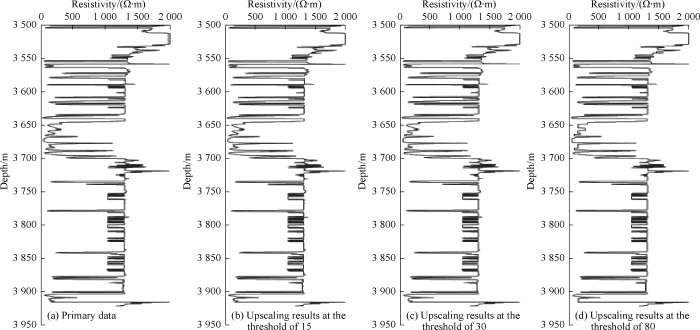
Therefore, for each bandwidth or threshold, we have a SSE value and a finite number of upscaled bands. During the upscaling for the first feature of the data, the threshold is changed from 0 to maximum of 1 400 with an incremental step of 2.5. These values for the second feature are 0-1 000 and 3, respectively. If the selected threshold values are small, more reservoir information can be preserved in the model and coarsening process begins from more heterogeneous regions. Zero threshold values will keep whole cells fine-grained and no coarse-graining will be carried out. The maximum threshold values will lead to total shrinkage of the cells into a uniform region and the entire model is converted into a block. Another important point in the upscaling process is to set the optimal threshold or appropriate bandwidth, which is very effective for increasing the computational efficiency. For this purpose, we proposed 3 different approaches, such as SSE change versus bandwidth, successive SSE changes, and intersection of two curves of SSE variability versus bandwidth and number of blocks-variability versus bandwidth. The SSE differential method is used to determine the optimal threshold or optimum bandwidth. Fig. 3 shows the upscaling results of the first feature (pore pressure). In the threshold setting of 50, SSE is 86 and the number of blocks is 940. When the threshold is 80, SSE is 176 and the number of blocks 682. Finally, when the threshold is equal to 100, SSE is 331 and the number of blocks is 554. It is indicated that the optimal threshold is 80. Fig. 4 shows the upscaling results of the second feature (resistivity). In the threshold setting of 15, SSE is 14 and the number of blocks is 800. When the threshold is 30, SSE is 48 and the number of blocks is 590. Finally, when the threshold is equal to 80, SSE is 192 and the number of blocks is 391. It is indicated that the optimal threshold value for this feature is 30.
Fig. 3.
Fig. 3.
Upscaling results of the first feature (pore pressure) at different thresholds.
Fig. 4.
Fig. 4.
Upscaling results of the second feature (resistivity) at different thresholds.
The upscaling method based on the adaptive bandwidth of the kernel function method depends on the calculation time and model accuracy. For example, if the goal of upscaling is simply to reduce the cost of the calculation, the larger bandwidth can be selected. Conversely, if the aim is to increase the model accuracy, smaller bandwidth shall be selected.
2.2. Simultaneous upscaling of two properties
Upscaling result becomes more reliable when it is carried out simultaneously for two or more reservoir properties. The purpose of upscaling of two features simultaneously is to obtain blocks with two equivalent quantities, and then, the fluid flow equations can be constructed based on these two features of the reservoir. In this paper, the optimal bandwidth of two features is first calculated and then the upscaling results are obtained. A final upscaled model is obtained by upscaling two features simultaneously using the minimum bandwidth and maximum bandwidth approaches, to ensure the number of upscaled blocks and the position of these blocks in both approaches are exactly the same.
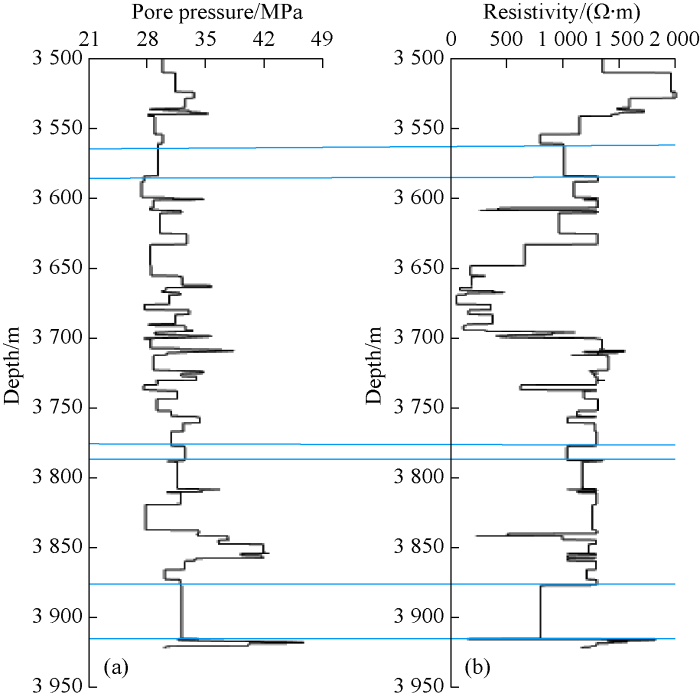
As above mentioned, the optimal threshold for the first feature is 80 and the number of upscaled blocks in this case is 682. The optimal threshold for the second feature is 30 and the number of upscaled blocks is 590. In the simultaneous upscaling of the two features, it is necessary to guarantee the number of blocks scaled on the basis of increment is equal and the location of these blocks is the same. In the minimum bandwidth method, the upscaling criterion is the smaller bandwidth compared to that of each of the two features. By comparing the upscaled blocks of the two features, the smaller one is calculated as the optimal block. Obviously, the number of blocks for the final upscaled model for both features is greater than the number in the single mode. The results of simultaneous upscaling of the two features using the minimum bandwidth approach are shown in Fig. 5. In this case, the number of final upscaled blocks is 848. The number of cells in the primary model is 2413. The upscaling error in minimum bandwidth approach is 390 for the first property and is 187 for the second property. The number of blocks in the upscaled model of two properties is the same and their position is also the same.
Fig. 5.
Fig. 5.
(a) Upscaling results of the first feature and (b) upscaling results of the second feature by the minimum bandwidth approach.
In the maximum bandwidth method, the upscaling criterion is the larger bandwidth than that of each of the two features. By comparing the upscaled blocks of two features, the larger one is calculated as the optimal block for simultaneous upscaling of the two features. Obviously, the number of blocks for the final upscaled model of both features is less than the number in the single mode. The results of simultaneous upscaling of the two features using the maximum bandwidth approach are shown in Fig. 6. In this case, the number of final upscaled blocks is 144. The upscaling error in maximum bandwidth approach for the first property is 1000 and that for the second property is equal to 1532.
Fig. 6.
Fig. 6.
(a) Upscaling results of the first feature and (b) upscaling results of the second feature by the maximum bandwidth approach.
In summary, the number of upscaled blocks in the model obtained from the minimum bandwidth and maximum bandwidth approaches for simultaneous upscaling of two reservoir properties is 848 and 144, respectively. An upscaled model with the same number and location of blocks is established using these two approaches, based on the bandwidth of the kernel function. Specifically, the size of the blocks in the maximum bandwidth approach is far greater than that in the minimum bandwidth approach.
In order to validate the reliability of these approaches, the upscaling results are compared with well log and test interpretation results (Table 1). It is shown that in some points, the estimated and upscaled pressure are equal. Furthermore, the difference between the actual pressure and the value based on the upscaling model is not high and is acceptable.
Table 1 Comparison between pore pressures obtained by different methods.
| Depth/m | Pressure from log interpretation/MPa | Pressure from test interpretation/MPa | Pressure calculated in the upscaled model/MPa |
|---|---|---|---|
| 3 500 | 28.89 | 30.08 | 29.03 |
| 3 571 | 30.27 | 30.74 | 30.27 |
| 3 617 | 29.55 | 30.02 | 29.64 |
| 3 676 | 30.41 | 31.25 | 30.41 |
| 3 687 | 30.83 | 31.10 | 30.83 |
| 3 721 | 29.65 | 30.43 | 29.82 |
| 3 776 | 30.96 | 32.11 | 30.70 |
| 3 810 | 32.54 | 32.90 | 32.50 |
| 3 855 | 31.87 | 31.56 | 31.78 |
| 3 886 | 31.81 | 31.19 | 31.77 |
| 3 913 | 34.41 | 30.84 | 31.11 |
| 3 919 | 30.20 | 30.90 | 30.20 |
3. Conclusions
This paper presents a new method for upscaling of two reservoir properties in one dimension using the adaptive bandwidth of kernel function method. This method decreases the grids number and keep the heterogeneity features of original fine model. In this method, the minimum and maximum bandwidth approaches are adopted for the simultaneous upscaling of two reservoir properties to remain fine scale of high property’s variability and coarsen the low variability areas. On this basis, the final upscaled model for two reservoir properties is established. The upscaling error rate in the minimum and maximum bandwidth approaches is dependent on the number of final blocks. From a computational point of view, the bandwidth upscaling method obtains non-uniform log with a number of log cells that represent, and the upscaling error of the minimum approach is less than the maximum one.
Nomenclature
${{\hat{f}}_{h}},\hat{g}$—density function;
h—bandwidth or smoothing parameter;
$h\left( {{x}_{i}} \right)$—bandwidth at ${{x}_{i}}$;
$K\left( \bullet \right)$—kernel function;
Kh—scale kernel function;
N—number of blocks.
Reference
Recent advances in statisticaland scaling analysis of earth and environmental variables
Numerical simulation of flow and heat transfer in fractured crystalline rocks: Application to the hot dry rock site in Rosemanowes (U.K.)
Use of higher moment for the description of upscaled, prosess independent relative permeabilities
Upscaling of small-scale heterogeneities to flow units for reservoir modeling
A new upscaling method for fractured porous media
Upscaling: A review
The effective diffusivities in porous media with and without nonlinear reactions
The behavior of effective rate constants for bimolecular reactions in an asymptotic transport regime
Multi-scale modeling of diffusion and reaction-diffusion phenomena in catalytic porous layers: Comparison with the 1D approach
Reduced order models for describing dispersion and reaction in monoliths
Three-dimensional hydraulic conductivity upscaling in groundwater modeling
Determining an appropriate finite element size for modelling the strength of undrained random soils
Upscaling and regionalizing hydraulic conductivity and effective porosity at watershed scale in deeply weathered crystalline aquifers
Efficient upscaling of hydraulic conductivity in heterogeneous alluvial aquifers
Spatial averaging of hydraulic conductivity in three-dimensional heterogeneous porous media
Upscaling of the permeability by multiscale wavelet transformations and simulation of multiphase flows in heterogeneous porous media
Stochastic analysis of three dimensional hydraulic conductivity upscaling in a heterogeneous tropical soil
Upscaling permeability for three-dimensional fractured porous rocks with the multiple boundary method
Power averaging for block effective permeability
Flow in heterogeneous porous media
Calculating equivalent permeability: A review
Application of wavelet transforms to reservoir-data analysis and scaling
Fractal-wavelet neural-network approach to characterization and upscaling of fractured reservoirs
Upscaling and simulation of waterflooding in heterogeneous reservoirs using wavelet transformations: Application to the SPE-10 model
De-noising by soft-thresholding
Pore structure characterization and classification using multifractal theory: An application in Santanghu Basin of western China
Noise reduction of nuclear magnetic resonance (NMR) transversal data using improved wavelet transform and exponentially weighted moving average (EWMA)
Remarks on some nonparametrice stimates of a density function
Nonparametric and semiparametric models: An introduction