Introduction
Drilling in deepwater faces many challenges, such as narrow safe drilling fluid density window of formation, marine geological disasters (shallow gas, shallow water flow and gas hydrate, etc.), low temperature environment in deepwater and unstable seabed, etc.[1,2,3,4]. Among them, the narrow safe drilling fluid density window of formation directly affects the safety, efficiency and success rate of drilling operations in deepwater[5]. In recent decades, dual-gradient drilling with gas injected[6], dual-gradient drilling with hollow spheres injected[7], dual-gradient drilling with subsea pump[8], and control mud cap drilling[9,10,11] have been developed at home and abroad to solve the problem of narrow safe drilling fluid density window in deepwater drilling[12,13].
Based on the idea of injecting light materials (hollow spheres and gas, etc.) into annulus to achieve dual-gradient drilling, a new dual-gradient drilling method using a separator mounted on the drill pipe to achieve dual-density in wellbore was proposed and a feasibility experiment was conducted in the laboratory. A dynamic wellbore pressure calculation method during drilling process with this method was proposed, and an optimization model for drilling parameters was established based on the calculation method. The optimization model aims at achieving the maximum drilling depth, while reducing the pressure difference between wellbore pressure and pore pressure as much as possible, while ensuring that the wellbore pressure is always within the narrow safe drilling fluid pressure window, so downhole complexities caused by imbalance wellbore pressure can be avoided effectively to make drilling safer and more efficient.
1. Feasibility experiment in the laboratory
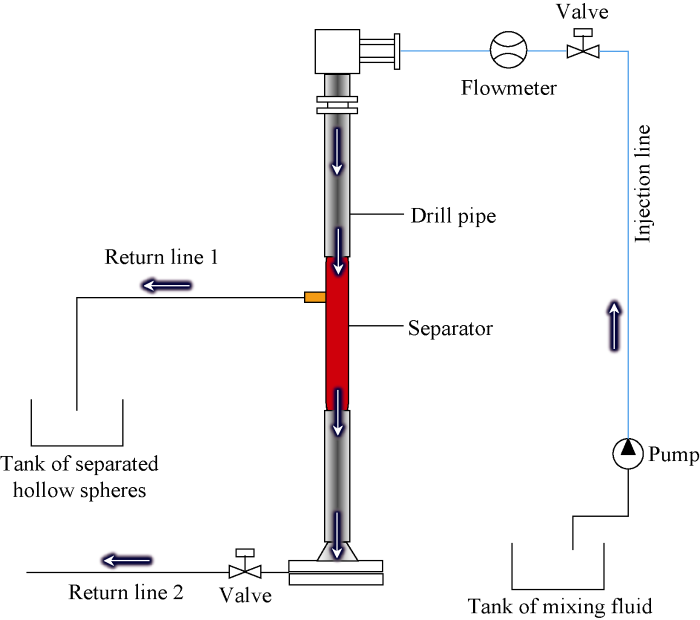
Fig. 1 shows the experimental apparatus for the new dual- gradient drilling, in which a separator is installed on the drill pipe to realize dual-density in wellbore. The hollow spheres separated by the separator will circulate upward with the annular fluid. Then, the concentration of hollow spheres is higher and the density of mixing fluid is lower in the annulus above the separator, while the concentration of hollow spheres is lower and the density of mixing fluid is higher in the annulus under the separator, achieving dual-pressure-gradient in the annulus.
Fig. 1.
Fig. 1.
An experimental apparatus for dual-gradient drilling.
Circulation-separation experiment was carried out in the laboratory to verify whether the separator designed is effective. During circulation, a mixing fluid (mainly made of hollow spheres and water) was injected through blue injection line after pressurization through the pump. When the mixing fluid flew through the separator, a part of the hollow spheres were separated and discharged through return line 1. The mixed fluid after separation was discharged through return line 2 at the bottom. The separation efficiency of the separator was obtained by measuring the mass of the hollow spheres separated by the return line 1 and the initially added hollow spheres. The experimental results are shown in Table 1. From the results, it can be seen that the separation efficiency of the separator is about 40%, which proves the effectiveness of the separator designed in this study.
Table 1 Experimental results at different injection volume fractions of hollow spheres.
| Injection volume fractions of hollow spheres/% | Mass of initially added hollow spheres/kg | Mass of the hollow spheres separated/kg | Separation efficiency/ % |
|---|---|---|---|
| 1 | 5 | 2.05 | 41.0 |
| 3 | 15 | 6.00 | 40.0 |
| 5 | 25 | 9.90 | 39.6 |
| 10 | 50 | 19.80 | 39.6 |
2. Calculation of dynamic wellbore pressure during drilling
2.1. Assumptions
In this paper, the following assumptions are made when calculating wellbore pressure: 1) separation efficiency is constant, and experimental results in the laboratory are taken for case study; 2) the influence of phase change on wellbore pressure is not taken into account; 3) the fluctuation pressure generated when the separated hollow sphere enters annulus is not taken into account.
2.2. Mathematical model
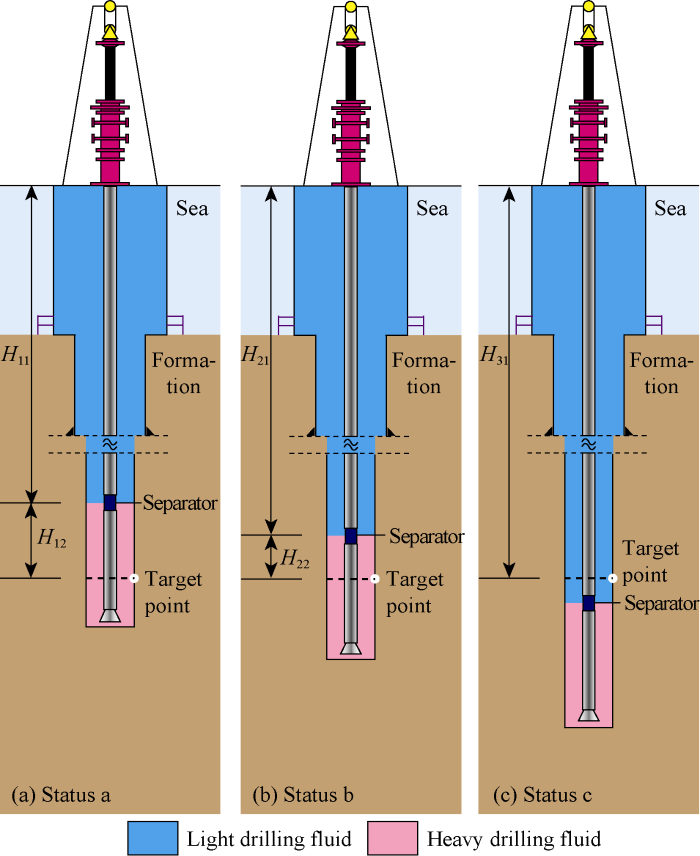
During drilling process, the separator moves down as well depth increases. For the target point (any point with the same depth in open-hole), the length of light drilling fluid section increases and the length of heavy drilling fluid section decreases. The dynamic distribution of light and heavy drilling fluids in the wellbore results in the change of wellbore pressure for the same depth, which is a characteristic that conventional drilling does not have (Fig. 2). From Fig. 2(a) to Fig. 2(c), the well depth increases and the separator moves down, therefore, the pressure at the target point changes.
Fig. 2.
Fig. 2.
Composition of wellbore pressure at target point during drilling.
For status (a), the pressure at target point during drilling is as follows:
Two methods commonly used to calculate frictional pressure drop are indirect method and direct method[14,15]. For indirect method, frictional pressure drop is obtained by calculating the Fanning friction coefficient (f) and the value of f is obtained by Colebrook relationship[16]. For direct method, empirical equation between frictional pressure drop and variables can be obtained based on the Bernoulli equation. Because the direct relationship between wellbore pressure and variables should be guaranteed when using optimization theory to solve optimization problems, rather than the non-linear relationship of iterative solution, the direct method was chosen to calculate frictional pressure drop in this study.
According to the above calculation method, the frictional pressure drops per unit lengths of light drilling fluid and heavy drilling fluid can be obtained respectively.
where ${{\rho }_{1}}={{V}_{0}}{{\rho }_{s}}+(1-{{V}_{0}}){{\rho }_{m}}$
${{\mu }_{1}}={{V}_{0}}{{\mu }_{s}}+(1-{{V}_{0}}){{\mu }_{m}}$
$\begin{matrix} {{\rho }_{2}}=(1-\varepsilon ){{V}_{0}}{{\rho }_{s}}+\left[ 1-(1-\varepsilon ){{V}_{0}} \right]{{\rho }_{m}} \\ {{\mu }_{2}}=(1-\varepsilon ){{V}_{0}}{{\mu }_{s}}+\left[ 1-(1-\varepsilon ){{V}_{0}} \right]{{\mu }_{m}} \\ \end{matrix}$
${{H}_{11}}=L-{{H}_{12}}$
${{H}_{12}}=L-(H-{{H}_{2}})$
The relationships between pressure at any point in wellbore under status (a) and the six variables (separation efficiency of separator, injection volume fraction, density of pure drilling fluid, distance between separator and bit, wellhead back pressure, displacement) have been established. For status (b) and (c), the wellbore pressures are:
It can be got from the above analysis,
In other words, the wellbore pressure at arbitrary depth in open-hole changes dynamically with the increase of well depth. Therefore, it is of great significance to study the optimization and design of drilling parameters for this drilling method.
3. Establishment and solution of optimization model for drilling parameters
3.1. Objective function
The purpose of the drilling parameter optimization model is to minimize borehole pressure difference and increase the ROP under the premise of ensuring the maximum drilling depth. As it is impossible to establish direct relationships between the drilling depth and six control variables, it is mathematically infeasible to take the drilling depth as an objective function to get the optimal solution. Therefore, the pressure difference between wellbore pressure and pore pressure at the current well depth was set as the objective function in this study. In addition, wellbore pressure in open-hole and six control variables were set as constraints, to minimize borehole pressure difference and ensure maximum drilling depth. The optimization model is expressed as follows:
where F(ε, V0, ρm, H20, pcp, Q) is the objective function, defined as the pressure difference at the current well depth. The expression is as follows:
where $p_{jd}^{*}={{p}_{cp}}+{{\rho }_{1}}g({{L}^{*}}-{{H}_{20}})\text{sin}\theta +\Delta {{p}_{f1}}({{L}^{*}}-{{H}_{20}})+$
${{\rho }_{2}}g{{H}_{20}}\text{sin}\theta +\Delta {{p}_{f2}}{{H}_{20}}$
3.2. Constraints
The simulation constraints are as follows:
In actual drilling operation, drilling equipment cannot adjust these parameters in real time automatically to reach the ideal values. Therefore, in order to keep the optimal variable value obtained by the optimization theory unchanged during the whole single drilling process, each variable was divided into n groups of data at equal intervals within the range of values in this study. In addition, n value should not be too large in order to avoid the dimension disaster in numerical calculation.
3.3. Solution of optimization model
The pressure difference at the current well depth was set as the objective function. The objective function changes dynamically during drilling. In addition, the number of constraints increases with the increase of well depth. The constraints also change dynamically because the wellbore pressure at any point in the open-hole varies. According to the above analysis, this issue is a constrained nonlinear dynamic optimization question. Because of the constraints of control variables, the constrained-nonlinear dynamic optimization problem is divided into finite static constrained-nonlinear optimization problems, which can be solved by optimization method.
The sequence quadratic programming (SQP) algorithm is considered as one of the most effective methods to solve the nonlinear optimization problem with constraints [17,18]. It has great application value in engineering. Thus, in this study, the SQP algorithm was used to solve the established optimization model. The fmincon function in MATLAB was selected as the objective function and SQP algorithm was used to solve the parameterized nonlinear programming (NLP) problem from the original optimal control problem.
4. Case study
The simulated well was a deepwater vertical well. Its basic data is as follows: The water depth is 1 000 m, and the well is 1200 m deep and cemented. The outer diameter and inner diameter of the riser are 660.4 mm and 609.6 mm, respectively. The outer diameter and inner diameter of drill pipe are 127 mm and 101.6 mm, respectively. The inner diameter of surface casing is 457.2 mm and the diameter of drill bit is 342.9 mm. The safe drilling fluid density window is narrow from 1 200 m to 2 200 m. In addition, the ultimate well depth set in simulation was 2 200 m. When drilling to this depth, the simulation ended.
4.1. Optimization results under different control parameters
In the simulation calculation, the control parameters (variables) were divided into equal intervals within the range of values. The intervals of injection volume fraction, density of pure drilling fluid, distance between separator and bit, wellhead back pressure and displacement were 0.02, 50 kg/m3, 100 m, 500 000 Pa and 3 L/s, respectively. The larger the value of n, the more the number of parameter groups, and the larger the range of variables under the same interval conditions is. When the narrow pressure window was 1.03-1.05 g/cm3, the drilling parameters were optimized at n values of 5, 6 and 7, respectively. The ranges of variables with different n values are shown in Table 2, and the optimization results are shown in Table 3 and Figs. 3-5.
Table 2 The range of drilling parameters under different n values.
| n value | Separation efficiency | Injection volume fraction | Density of pure drilling fluid/(kg•m-3) | Distance between separator and bit/m | Wellhead back pressure/Pa | Displacement/ (L•s-1) |
|---|---|---|---|---|---|---|
| 5 | 0.4 | [0.30, 0.38] | [1 000, 1 200] | [100, 500] | [0, 2 000 000] | [30, 42] |
| 6 | 0.4 | [0.30, 0.40] | [1 000, 1 250] | [100, 600] | [0, 2 500 000] | [30, 45] |
| 7 | 0.4 | [0.30, 0.42] | [1 000, 1 300] | [100, 700] | [0, 3 000 000] | [30, 48] |
Table 3 The optimization results under different range of drilling parameters.
| n value | Optimization results of drilling parameters | Maximum drilling depth/m | |||||
|---|---|---|---|---|---|---|---|
| Separation efficiency | Injection volume fraction | Density of pure drilling fluid/(kg•m-3) | Distance between separator and bit/m | Wellhead back pressure/Pa | Displacement/ (L•s-1) | ||
| 5 | 0.4 | 0.30 | 1 150 | 100 | 1 000 000 | 30 | 1 440 |
| 6 | 0.4 | 0.34 | 1 250 | 100 | 500 000 | 36 | 1 510 |
| 7 | 0.4 | 0.38 | 1 300 | 100 | 500 000 | 42 | 1 550 |
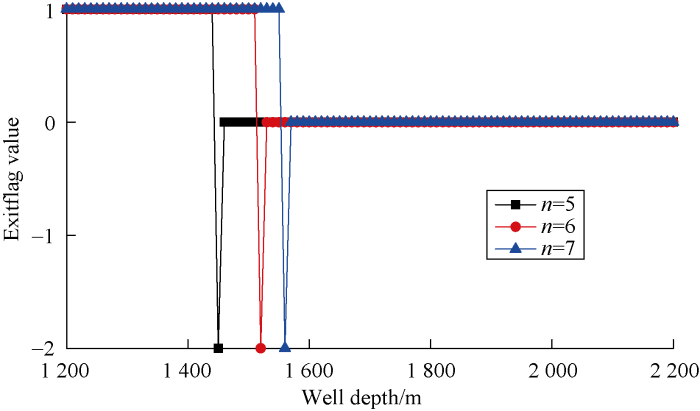
Fig. 3 shows the characterization value of maximum drilling depth (Exitflag value) under different ranges of variables. Exitflag value is 1 in the well depth that can be drilled under constraints, but not 1 in the well depth that can’t be drilled. Therefore, the maximum drilling depth can be obtained according to Exitflag value at each depth during optimization process. It can be seen from Table 3 and Fig. 3, when n is 5, 6 and 7 respectively, the maximum drilling depth is 1 440, 1510 and 1 550 m. With the increase of n value, the range of variable values becomes wider, so better drilling parameters can be selected to achieve greater drilling depth.
Fig. 3.
Fig. 3.
The value to characterize the maximum drilling depth under different range of variables.
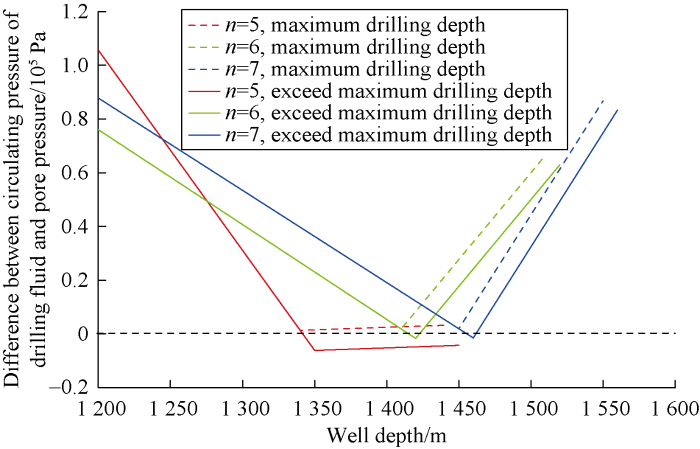
Fig. 4 shows the difference between circulating pressure of drilling fluid and pore pressure under different ranges of variables. The dotted line in the figure shows the pressure difference at different depths when the well is drilled to the maximum drilling depth under the optimal drilling parameters, and the solid line in the figure shows the pressure difference at different depths after the drilling reaches the maximum depth. It can be seen from Fig. 4 that under different n values, when the well depth increases from 1 200 m to the corresponding maximum drilling depth under optimal variable parameters, the difference between circulating pressure of drilling fluid and pore pressure at any point in the open-hole is greater than zero. In other words, the wellbore pressure at any point in the open-hole is within the narrow safe pressure window, effectively avoiding downhole complexities caused by improper wellbore pressure. When the well depth exceeds the designed maximum drilling depth, a negative pressure difference occurs. In other words, circulating pressure of drilling fluid at some depth in the open-hole is lower than the formation pore pressure, and downhole complexities may come up, not conducive to safe and efficient drilling.
Fig. 4.
Fig. 4.
The difference between circulating pressure of drilling fluid and pore pressure under different ranges of variables.
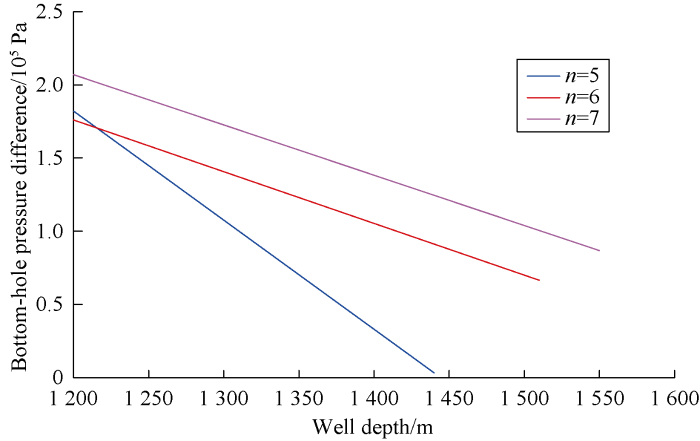
Fig. 5 shows the bottom-hole pressure difference while drilling under different ranges of variables, that is, the bottom-hole pressure difference when the bit first drills to a well depth. It can be seen from Fig. 5 that under different ranges of variables, in the process of drilling to 1 440, 1 510, 1 550 m with the optimal variable value, the bottom-hole pressure difference is less than 2.5×105 Pa, which is much smaller than the bottom-hole pressure difference in conventional drilling (2.0×106 Pa). The smaller bottom-hole pressure difference obtained by the optimization model is good for improving the ROP, protecting reservoirs and reducing the comprehensive cost of drilling.
Fig. 5.
Fig. 5.
The bottom-hole pressure difference under different ranges of variables.
4.2. Optimization results under different range of narrow safe pressure margins
When n was 6, the drilling parameters were optimized under different ranges of safe pressure margins (1.03-1.04 g/cm3, 1.03-1.05 g/cm3, 1.03-1.06 g/cm3). The optimization results are shown in Table 4 and Figs. 6-8.
Table 4 The optimization results of drilling parameters under different ranges of narrow safe pressure margins.
| Narrow safe pressure margins/ (g•cm-3) | Optimization results of drilling parameters | Maximum drilling depth/m | |||||
|---|---|---|---|---|---|---|---|
| Separation efficiency | Injection volume fraction | Density of pure drilling fluid/(kg•m-3) | Distance between separator and bit/m | Wellhead back pressure/Pa | Displacement/ (L•s-1) | ||
| 1.03-1.04 | 0.4 | 0.30 | 1 200 | 100 | 500 000 | 42 | 1 340 |
| 1.03-1.05 | 0.4 | 0.34 | 1 250 | 100 | 500 000 | 36 | 1 510 |
| 1.03-1.06 | 0.4 | 0.32 | 1 250 | 100 | 500 000 | 39 | 2 200 |
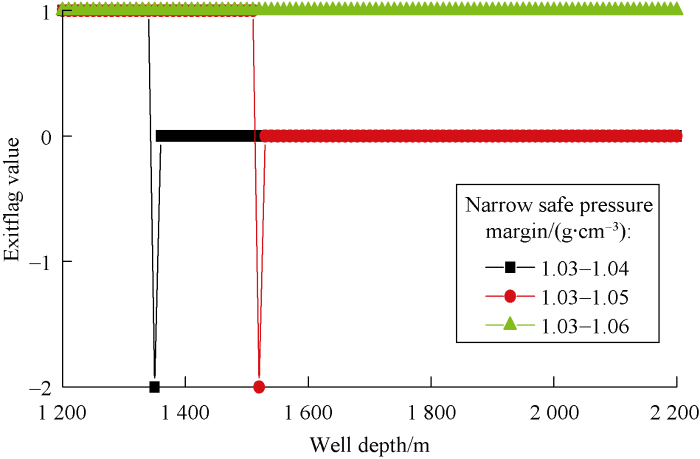
Fig. 6 shows the characterization value of maximum drilling depth (Exitflag value) under different ranges of narrow safe pressure margins. It can be seen from Table 4 and Fig. 6, when narrow safe pressure margins are 1.03-1.04 g/cm3, 1.03-1.05 g/cm3 and 1.03-1.06 g/cm3, the maximum drilling depths are 1 340 m, 1 510 m and 2 200 m respectively. With the widening of the safe pressure margins, better drilling parameters can be found to achieve greater drilling depth.
Fig. 6.
Fig. 6.
The value to characterize the maximum drilling depth under different range of narrow safe pressure margins.
Fig. 7 shows the difference between circulating pressure of drilling fluid and pore pressure under different narrow safe pressure margins. It can be seen from Fig. 7 that under different range of narrow safe pressure margins, when the well depth increases from 1 200 m to the corresponding maximum drilling depth with optimal variable parameters (the dotted line), the difference between circulating pressure of drilling fluid and pore pressure at any point in the open-hole is greater than zero. When the well depth exceeds its maximum drilling depth (the solid line), negative pressure difference occurs, in other words, circulating pressure of drilling fluid at some depth in the open-hole is lower than the formation pore pressure, and downhole complexities may happen, threatening safe and efficient drilling. In addition, the optimization results show that when the pressure margins is 1.03-1.06 g/cm3, the well can be drilled to 2 200 m (the limiting well depth) by using the optimal variable values, therefore, the solid line diagram corresponding to 1.03-1.06 g/cm3 is omitted in the figure.
Fig. 7.
Fig. 7.
The difference between circulating pressure of drilling fluid and pore pressure under different ranges of narrow safe pressure margins.
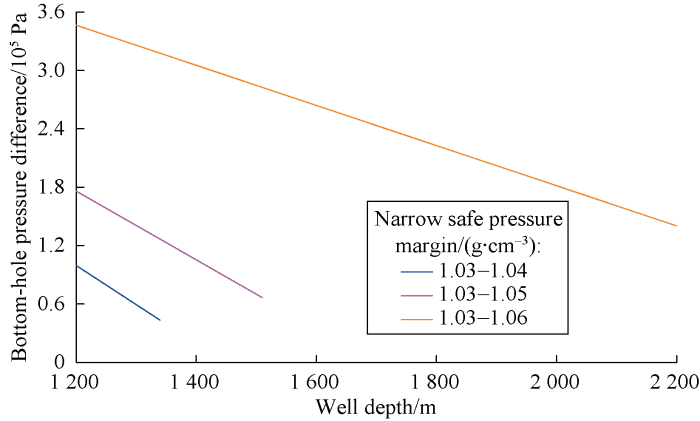
Fig. 8 shows the bottom-hole pressure difference while drilling under different narrow safe pressure margins. It can be seen that under three different narrow safe pressure margins, the bottom-hole pressure difference is less than 3.6×105 Pa in the process of drilling to 1 340, 1 510, 2 200 m with the optimal variable values. The smaller bottom-hole pressure difference is good for improving the ROP, protecting reservoirs and reducing the comprehensive cost of drilling.
Fig. 8.
Fig. 8.
The bottom-hole pressure difference under different ranges of narrow safe pressure margins.
5. Conclusions and suggestions
Experimental results in the laboratory show that the separator has good separation effect under different injection volume fractions of hollow spheres, and the separation efficiency is basically constant, which proves the effectiveness of downhole separation and the feasibility of realizing dual-gradient in wellbore. After optimizing the key control parameters such as separator position and separation efficiency, the wellbore pressure profile can be optimized to better adapt to the narrow pressure margins in deepwater and reach greater drilling depth. The optimized bottom-hole pressure difference is much lower than that of conventional drilling, which is conducive to improving the ROP, reducing reservoir damage and reducing the comprehensive cost of drilling. This study mainly focuses on optimization of drilling parameters for offshore vertical wells. Therefore, optimization of drilling parameters for offshore horizontal or deviated well is also an important task to study.
Nomenclature
Di—outer diameter of annulus, cm;
Dp—inner diameter of annulus, cm;
f—Fanning friction coefficient;
F—objective function;
g—acceleration of gravity, 9.81 m/s2;
H—total well depth, m;
H2—distance between separator and bit, m;
H11—length of light drilling fluid section under status (a), m;
H12—length of heavy drilling fluid section between separator and target point under status (a), m;
H20—distance between separator and target point, m;
H21—length of light drilling fluid section under status (b), m;
H22—length of heavy drilling fluid section between separator and target point under status (b), m;
H31—length of light drilling fluid section under status (c), m;
L—depth of target point, m;
$L_{{}}^{*}$—current well depth, m;
pa—pressure of target point under status (a), Pa;
pb—pressure of target point under status (b), Pa;
pc—pressure of target point under status (c), Pa;
pcp—wellhead back pressure, Pa;
$p_{\text{p}}^{*}$—formation pore pressure at current well depth, Pa;
$p_{jd}^{*}$—bottom-hole pressure at current well depth, Pa;
pi—wellbore pressure at any position in open-hole during drilling, Pa;
pp—the lower bound of formation pressure margins, i.e. formation pore pressure, Pa;
pf—the upper bound of formation pressure margins, i.e. formation fracture pressure, Pa;
Q—displacement, L/s;
V0—injection volume fraction of hollow spheres;
ε—separation efficiency of separator;
θ—well inclination angle, (°);
μm—plastic viscosity of pure drilling fluid, Pa•s;
μs—viscosity of hollow spheres, Pa•s;
μ1—plastic viscosity of light drilling fluid, Pa•s;
μ2—plastic viscosity of heavy drilling fluid, Pa•s;
ρm—density of pure drilling fluid, kg/m3;
ρs—density of hollow spheres, kg/m3;
ρ1—density of light drilling fluid, kg/m3;
ρ2—density of heavy drilling fluid, kg/m3;
Δpf1—frictional pressure drop per unit length of light drilling fluid, Pa/m;
Δpf2—frictional pressure drop per unit length of heavy drilling fluid, Pa/m.
Subscript:
l—minimum value;
u—maximum value;
i—position at different depth.
Reference
Explaining the storegga slide
Collection of innovative answers to solve the main problematics encountered when drilling deep water prospects
A global satellite survey of density plumes at river mouths and at other environments: Plume configurations, external controls, and implications for deep-water sedimentation
Prediction of wax precipitation region in wellbore during deep water oil well testing
Current situation and developing trend of petroleum drilling technologies in deep water
Feasibility study on the reduction of hydrostatic pressure in a deep water riser using a gas lift method
Multi- gradient drilling method and system: 006530437
Subsea mud-lift drilling joint industry project: Delivering dual gradient drilling technology to industry
Controlled mud-cap drilling for subsea applications: Well-control challenges in deep waters
Mathematical modeling of unsteady flow in controlled mud-cap drilling
Modeling and analysis of unsteady flow behavior in deepwater controlled mud-cap drilling
Development of transient heat transfer model for controlled gradient drilling
Numerical model for evaluating well kick and lost circulation during managed pressure drilling
A new model for laminar, transitional, and turbulent flow of drilling muds
A three layer hydraulic program for effective cuttings transport and hole cleaning in highly deviated and horizontal wells
Experiments with fluid friction in roughened pipes
3D trajectory optimization of the SAR imaging seeker based on SQP
Integrated reduced Hessian SQP algorithm for distillantion column optimization