Introduction
With exploration and development of shale oil and gas, the wellbore instability problem in shale interval has drawn more and more attention[1,2]. The anti-collapse drilling fluid technology taking advantage of the “synergistic effect of multiple mechanisms” has been widely used in the drilling of shale formation[3]. That involves improving the stability of shale borehole by “sealing, inhibiting and chemical activity balance”. But how to accurately calculate the safe drilling mud density window considering shale hydration stress and related strength damage when interacting with drilling fluid is still a key problem waiting to be solved urgently. Compared with the method to characterize the macro hydration deformation by statistically analyzing from the microscopic point of view and then upscale[4,5,6], shale macroscopic constitutive model analysis is much simpler[7,8,9]. Heidug, Ghassemi and Zhou et al. proposed the chemo-poro-elastic constitutive equation of shale and concluded that the effective stress of shale was influenced by shale deformation, pore pressure and variation of pore fluid chemical potential[7,8,9]. Zhang et al.[10,11] observed the hydration induced fracture propagation with CT scanning and found that the variation of hydration stress was not consistent with what Heidug-Wong generalized Biot effective stress equation described[7]. In addition, the hydration of clay minerals can cause the propagation of fractures and strength damage of shale[10,11,12,13,14], which hasn’t been considered by the chemo-poro- mechanical model.
In this work, based on the variation law of hydration stress, the Heidug-Wong generalized Biot effective stress equation[7] has been corrected, and the Weibull statistical model is used to describe the hydration strain-related strength damage. Considering the drilling fluid sealing layer on the shale, by solving pore fluid flowing and solute diffusion equations, the pore pressure and solute concentration at the borehole wall can be calculated, and then shale safe drilling mud density window can be predicted. The method can be used to accurately calculate the collapse pressure, fracturing pressure and its variation with time in the shale section, to provide basis for the design of anti-collapse drilling fluid.
1. Correction of generalized effective stress equation and statistically modeling of shale hydration strength damage
1.1. Variation pattern of shale hydration stress and correction of Heidug-Wong generalized effective stress equation
1.1.1. Width of hydration induced fracture in meso scale and variation pattern of hydration stress
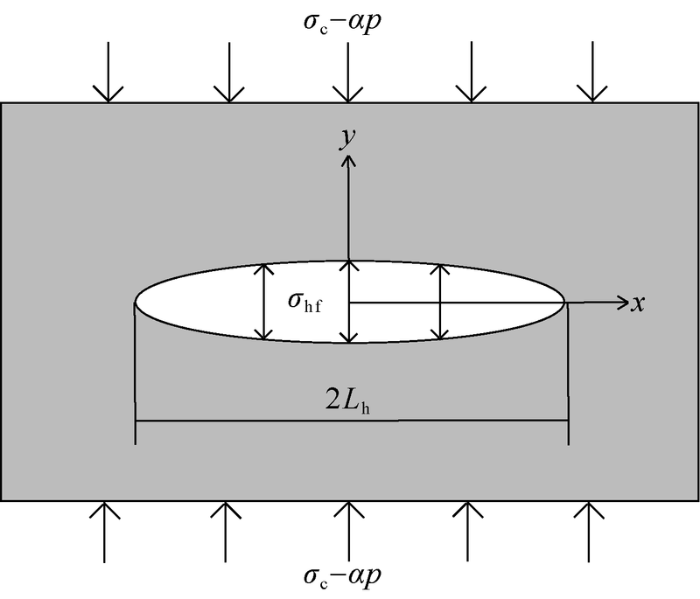
Fig. 1.
Griffith hydration indued fracture model[9].
Hydration swelling stress (\({{\sigma }_{\text{hf}}}\)) acts as tensile stress in fracture, which can overcome fracture closing pressure (\({{\sigma }_{\text{c}}}-\alpha p\)) and induce fracture propagation. According to Griffith principle, hydration induced fracture width can be expressed as:
Ignoring the influence of pore pressure, then
Zhang et al.[10-11] observed propagation of hydration induced fractures in shale under the conditions of 0.03 MPa pore pressure, 0.10 MPa confining pressure and 0.03 MPa pore pressure, 20.0 MPa confining pressure, respectively. Two main trends of fracture propagation were observed, (1) \(\Delta y\left( x \right)\) kept decreasing, then \({{\sigma }_{\text{hf}}}\) was smaller than \({{\sigma }_{\text{c}}}\) and \({{\sigma }_{\text{hf}}}\) kept decreasing; (2) \(\Delta y\left( x \right)\) firstly increased and then decreased, then firstly \({{\sigma }_{\text{hf}}}\) was larger than \({{\sigma }_{\text{c}}}\), and with time going, \({{\sigma }_{\text{hf}}}\) turned smaller than \(σ_c\) and \({{\sigma }_{\text{hf}}}\) kept decreasing. In both processes, \(σ_c\) was constant and it could be inferred that \({{\sigma }_{\text{h}}}\) was highest at the initial stage and then decreased with time. As Heidug et al.[7] reported, the main driving force for shale hydration swelling was chemical potential variation in clay mineral spacing. At first, chemical potential difference between pore fluid and clay mineral spacing was the highest, resulting in highest hydration stress. With transport of solute and diffusion of water molecules, the chemical potential difference between pore fluid and clay mineral spacing decreases, and accordingly the variation of chemical potential in clay mineral spacing decreases, leading to reduction of hydration stress. Then, it can be inferred,
1.1.2. Solute transport in shale and residual hydration swelling pressure
Shale contains a lot of clay minerals (Fig. 2a). Water and solute molecules can transport through multi-scale pores in shale (Fig. 2b), including spacing between clay mineral layers in nano-scale and macro-pores[15]. Osmotic flow of fluid in macro-pores is influenced by shale membrane efficiency, and when the membrane efficiency is equal to 0, there is no osmotic flow. But for clay mineral spacing, transport of solute and water molecules driven by chemical potential difference will result in hydration swelling stress and induce increase of clay mineral spacing. With chemical potential difference decreasing, hydration swelling stress will decrease until it is balanced by confining stress (Fig. 2c). At this point, transport of solute and water molecules are stopped and chemical difference between pore fluid and clay mineral spacing keep constant, then the residual hydration swelling stress in clay minerals spacing is the residual swelling pressure[15,16].
Fig. 2.
Schematic diagram of shale, and solute transport and hydration stress distribution in shale.
1.1.3. Correction of generalized Biot effective stress equation for shale
The generalized Biot effective stress equation proposed by Heidug-Wong is[7]:
Integrating items by t at both sides of equation 6:
Assuming only one kind of solute in the pore fluid can cause hydration swelling of shale. According to equation 3, considering the residual hydration swelling pressure, the following equation can be used to describe the hydration stress:
1.2. Weibull statistical model of shale strength damage due to hydration swelling
Hydration swelling can induce fracture propagation in shale and thus strength damage[10,11,12,13,14]. Different theoretical models were proposed to describe the relationship between meso scale fracture generation and macroscopic strength damage of rock[20,21,22,23,24,25], among which Weibull statistical model has been widely used[23,24,25]. The experimental results of Zhang et al.[11] show with shale hydration swelling strain increasing from 7.16×10-4 to 1.662×10-3 and 3.170×10-3, the Mancos shale strength, which was 65.7 MPa under 3.5 MPa confining pressure before hydration, reduced from 46.6 MPa to 31.4 MPa and then 0 MPa (broken), respectively. Hence, hydration swelling strain can be considered as element strength parameter, then Weibull statistical damage model of shale related to hydration strain can be expressed as:
Under interaction with drilling fluid, the shale failure under in-situ stress can be regarded as two-stage loading by hydration swelling stress and shear stress, and the total shale damage can be expressed as [25]:
Assuming shale strength damage was 0 before hydration, then
According to Heidug-Wong[7], there was local physical-chemical equilibrium during shale hydration process, and the hydration rate of shale was much faster than strain rate. Then, it can be assumed that the pore pressure and external constraints are constant during the hydration swelling process, and the hydration swelling volumetric strain can be expressed as:
Assuming only one kind of solute in the pore fluid can cause shale hydration swelling, if\[{{\omega }_{1}}\text{=}\frac{\alpha -1}{{{G}_{\text{K}}}}{{\omega }_{\text{k0}}}\frac{\partial \mu }{\partial c}\], inte-grate both sides of equation 13 by t, and include equation 10, then:
It can be seen from equation 14 that with the amount of solute or water molecules increasing in shale, the strength damage increases.
2. Calculation model of safe drilling mud density window
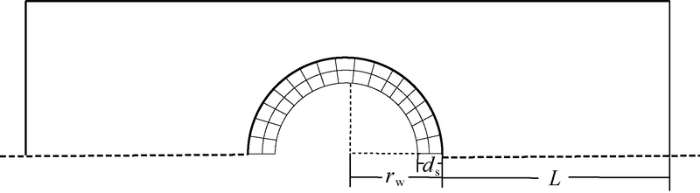
2.1. Wellbore model considering sealing layer of drilling mud on shale surface
Asphalt, high molecular polymer can adhere to the surface of the shale. Besides, the polyalcohol, silicate, aluminum-based stabilizer, etc. can form precipitates plugging pores in shale at the front edge of the filtrate. Therefore, the drilling fluid sealing layer is composed of adhesion layer and surface shale filled with plugging agents, which is like none-perfect semipermeable membrane, and is much denser than the original shale. Based on these facts, the model of the wellbore is established, as shown in Fig. 3 and there is a sealing layer on the borehole wall, which can affect the transport of water and solute from the drilling fluid to the borehole wall, thereby affecting the pore pressure and solute concentration at the borehole wall.
Fig. 3.
1/2 wellbore model.
2.2. Mass balance equation for pore fluid flowing through sealing layer and shale
Mass balance equation for pore fluid flowing in shale is[2]:
Based on the continuity equation, ignoring the influence of chemical potential, solid deformation, and solute adsorption on fluid flow, the pore fluid mass balance equation of the sealing layer can be expressed as:
Assuming that the relationship between permeability and porosity of the sealing layer is consistent with that of shale, then the porosity of sealing layer can be expressed as[14]:
As shown in Fig. 3, the boundary conditions for pore fluid flowing are:
2.3. Mass balance equation for solute diffusion through sealing layer and shale
Mass balance equation for solute diffusion in shale is[2]:
Mass balance equation of solute in sealing layer is:
According to equations 4 and 5, assuming that the diffusion correction coefficients and pore geometric characteristic parameter of the sealing layer are consistent with those of shale, then the diffusion coefficients of the sealing layer can be expressed as follows:
At infinite distance, as the content of K+ or other prohibition agents in shale pore fluid are very low and negligible, the diffusion boundary conditions are:
2.4. Method to calculate safe drilling mud density window considering shale hydration stress and shale strength damage
According to strain equivalence hypojournal proposed by Lemaitre J[26], considering strength damage, the modified effective strength equation can be expressed as:
\[\sigma _{i\text{,}j}^{\text{*}}=\frac{{{\sigma }_{i\text{,}j}}-\left[ \alpha p-\left( {{\omega }_{\text{0}}}\frac{\partial c}{\partial t}+{{\alpha }_{\text{d}}}{{\pi }_{\text{d}}} \right) \right]{{\delta }_{i\text{,}j}}}{1-D}\]
Mohr-Coulomb failure criterion is one of the shear failure strength criteria widely used in borehole stability analysis[23], which can be expressed as
Tensile failure strength criterion can be expressed as:
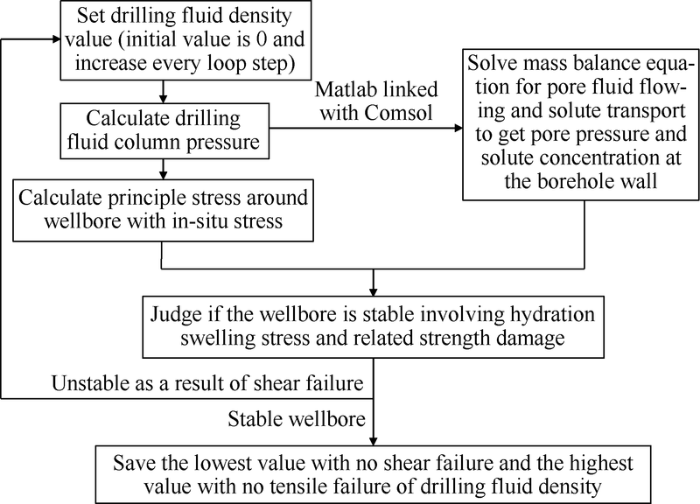
Equations (15) and (16) and equations (19) and (20) are solved by Comsol finite element software to obtain borehole wall pore pressure and solute concentration, respectively. Thereafter, strength damage related to solute concentration is calculated by equation (14). Based on the in-situ stress, the stress distribution around the well and the principal stress of the borehole wall are calculated by using MATLAB software. The collapse pressure and fracturing pressure are calculated based on the shear and tensile failure criteria considering the hydration swelling stress and strength damage. The flow chart is shown in Fig. 4.
Fig. 4.
Flow chart for calculating safe drilling mud density window of shale section.
3. Calculation of shale safe drilling mud density window
The anti-collapse drilling fluid mainly improves wellbore stability by making use of its sealing and inhibition properties. If there is osmotic flow in shale, the concentration of inorganic salt in the drilling fluid can be increased to induce pore fluid to flow out of shale into drilling fluid, to reduce pore pressure and improve wellbore stability. According to the test results of plugging, diffusion and swelling parameters (Table 1) of shale in literatures [2, 15-18, 23-25, 27-29], the method presented in this paper was used to calculate the safe drilling mud density window. The influence of drilling fluid anti-collapse performance on borehole wall pore pressure, solute concentration, hydration swelling stress, hydration strength damage and safe drilling mud density window were analyzed.
Table 1 Parameters for shale safe drilling mud density window calculation.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ø | 7% | σv | 56 MPa |
| K | 1.0×10-9 μm2 | σH | 53 MPa |
| Ks | (0.01-1.00)×10-10 μm2 | σh | 42 MPa |
| De | 1×10-10 m2/s | p0 | 22 MPa |
| Des | (0.01-1.00)×10-11 m2/s | 30 MPa | |
| σm | 0.2 | GK | 8.93 GPa |
| σms | 0.3-0.5 | GKm | 9.76 GPa |
| ds | 1-3 mm | σt | 2 MPa |
| cf | 1 341.4 mol/m3 | C | 28 MPa |
| η | 1.0 mPa•s | φ | 32° |
| c0 | 0 | α | 0.9 |
| GKf | 2.2 GPa |
3.1. Influence of drilling fluid sealing performance on borehole wall pore pressure and safe drilling mud density window
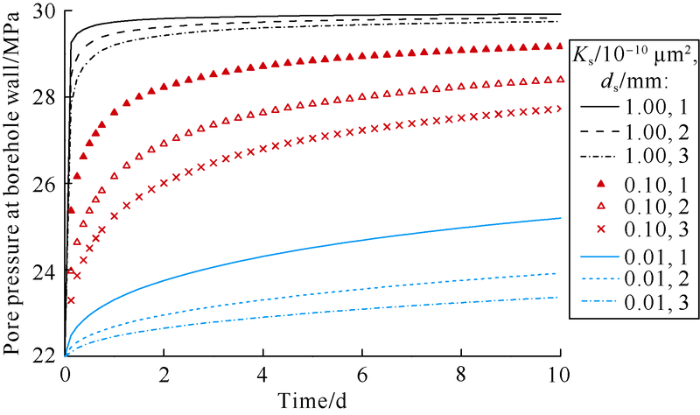
3.1.1. Influence drilling fluid sealing performance on transmission of pore pressure at borehole wallIf there is no osmotic flow in shale, the parameters which can influence borehole wall pore pressure are the thickness and permeability of the sealing layer. The parameters in Table 1 were used to calculate the pore pressure at the borehole wall at different sealing layer permeabilities and thicknesses (Fig. 5). (1) The pore pressure is positively correlated with time, it rises rapidly in the initial stage, after inflection points appearing on the curve within 1.5 days, then it rises slowly. (2) When the thickness of the sealing layer is constant, the lower the permeability of the sealing layer, the lower the pore pressure is. (3) The effect of sealing layer thickness on pore pressure change decreases significantly with the increase of sealing layer permeability. For example, when Ks=1×10-10 μm2, the change of sealing layer thickness has little influence on borehole pore pressure, and after 10 days the three curves of pore pressure at different sealing layer thicknesses nearly coincide. (4) When the permeability of the sealing layer is constant, the smaller the thickness of the sealing layer, the higher the pore pressure will be. It can be seen that permeability and thickness of sealing layer are the key factors controlling pore pressure transmission.
Fig. 5.
Influences of sealing layer permeability and thickness on pore pressure at borehole wall.
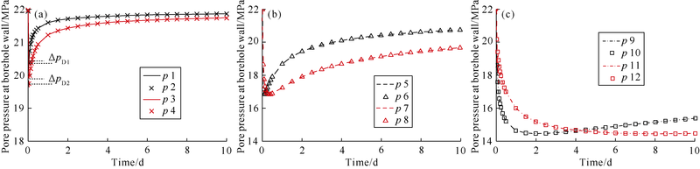
3.1.2. Influence of osmotic flow on borehole wall pore pressureAccording to the pore fluid flow and solute transport model, if the activity of drilling fluid (inorganic salt concentration) remains constant, the factor influencing borehole pore pressure include thickness, permeability and membrane efficiency of sealing layer. We set p0 to be 30 MPa, ds to be 1, 2 mm, sealing layer membrane efficiency to be 0.3, 0.5. Other parameters were the same as listed in Table 1, the borehole wall pore pressure was calculated (Table 2 and Fig. 6).
Table 2 Parameter combinations for calculating pore pressure at borehole wall.
| Parameter combinations | Ks/ 10-10 μm2 | σms | ds/ mm | Parameter combinations | Ks/ 10-10 μm2 | σms | ds/ mm |
|---|---|---|---|---|---|---|---|
| p 1 | 1.00 | 0.3 | 1 | p 7 | 0.10 | 0.3 | 2 |
| p 2 | 1.00 | 0.5 | 1 | p 8 | 0.10 | 0.5 | 2 |
| p3 | 1.00 | 0.3 | 2 | p 9 | 0.01 | 0.3 | 1 |
| p 4 | 1.00 | 0.5 | 2 | p 10 | 0.01 | 0.5 | 1 |
| p 5 | 0.10 | 0.3 | 1 | p 11 | 0.01 | 0.3 | 2 |
| p 6 | 0.10 | 0.5 | 1 | p 12 | 0.01 | 0.5 | 2 |
Fig. 6.
Pore pressures at the borehole wall under various parameter combinations.
As shown in Fig. 6, if there is osmotic flow in shale, under the influence of the sealing layer: (1) The pore pressure of borehole wall gradually decreases to the minimum with time, then increases gradually and tends to be stable. (2) When the thickness of the sealing layer is constant, the lower the permeability of the sealing layer, the larger the reduction magnitude of borehole pore pressure, and the slower the increase rate of the pore pressure after dropping to the minimum will be. For example, when ds=1 mm, σms=0.3, if the sealing layer permeability reduces from 1.00×10-10 μm2 to 0.10×10-10 μm2, and 0.01×10-10 μm2, the minimum pore pressure will reduce from 20.39 MPa to 16.86 MPa and 14.44 MPa, respectively. Accordingly, after 10 days, the borehole wall pore pressure will reduce from 21.87 MPa to 20.76 MPa and 15.36 MPa. (3) When the thickness of sealing layer increases, both the rates of pore pressure decreasing and then increasing will slow down, and the lowest value of pore pressure slightly decreases. For example, when Ks=0.10×10-10 μm2, ds increases from 1 mm (p5) to 2 mm (p7), the lowest value of pore pressure decreases from 16.86 MPa to 16.84 MPa, and 10 days later pore pressure decreases from 20.76 MPa to 19.67 MPa. (4) The effect of increasing sealing layer membrane efficiency on borehole wall pore pressure decreases with the drop of sealing layer permeability. For example, when Ks=1.00×10-10 μm2, σms increases from 0.3 to 0.5, the minimum pore pressure decreases by ΔpD1=0.03 MPa when ds=1 mm, and decreases by ΔpD2=0.16 MPa when ds=2 mm. When Ks=0.10×10-10 μm2 and 0.01×10-10 μm2, the change of membrane efficiency has little influence on borehole pore pressure, and the curves of pore pressure almost coincide. It can be seen that the permeability and thickness of the sealing layer are the key factors affecting the pore pressure.
3.2. Effects of drilling fluid sealing and inhibition
performance on shale effective stress and strength damage
According to the generalized effective stress equation, the hydration swelling stress of shale at borehole wall \[{{\sigma }_{\text{he}}}\] can be expressed as:
According to the solute diffusion equation, generalized effective stress equation, and shale hydration strength damage equation, if the pore pressure remains constant, the factors influencing shale hydration stress at borehole wall include solute concentration, shale hydration swelling coefficient and residual swelling pressure; and the factors influencing shale hydration strength damage (equation 14) include γ and m. If the value of m is 1.5 and γ ranges from 0.005 to 0.030, the D will range from 0 to 0.9945.
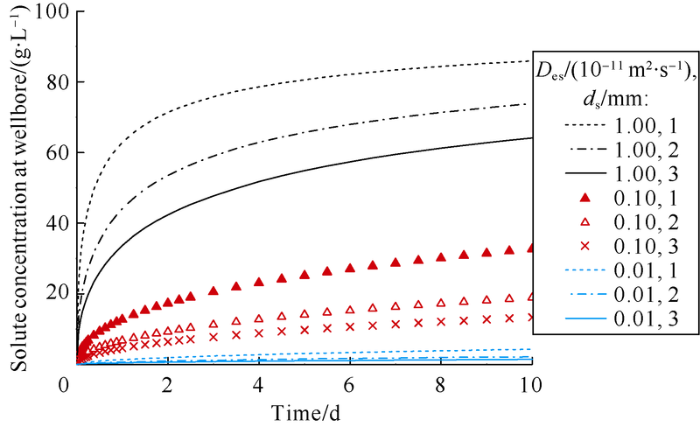
Given the diffusion coefficient of solute in shale of 1× 10-10 m2/s, and the diffusion coefficient in the sealing layer of (0.01-1.00)×10-11 m2/s, the thickness of the sealing layer of 1-3 mm, the concentration of inhibitor in shale of zero, and the concentration of inhibitor (KCl) in drilling fluid of 100 g/L, the solute concentrations at the borehole wall with different diffusion coefficients were calculated (Fig. 7). The results show that: (1) The solute concentration is positively correlated with time, rise rapidly at the initial stage, and then rises slowly after inflection point occurring about 1 day later. (2) The lower the sealing layer diffusion coefficient, the lower the solute concentration at the borehole wall is, and with time going, solute concentration varies greatly at the initial stage with diffusion coefficient of sealing layer and tends to be stable in the later stage. (3) The thicker the sealing layer, the lower the solute concentration at the borehole wall will be, similarly, with the time going, the thickness of sealing layer has more significant effect on solute concentration at the borehole wall in the initial stage, and later the effect tends stable. Clearly, decrease of sealing layer diffusion coefficient can reduce the solute diffusion. According to equation (5), the effective diffusion coefficient of solute is related to external constrains, with the increase of external compressive stress, solute diffusion reduces.
Fig. 7.
Influence of sealing layer diffusion coefficient on solute concentration at borehole wall.
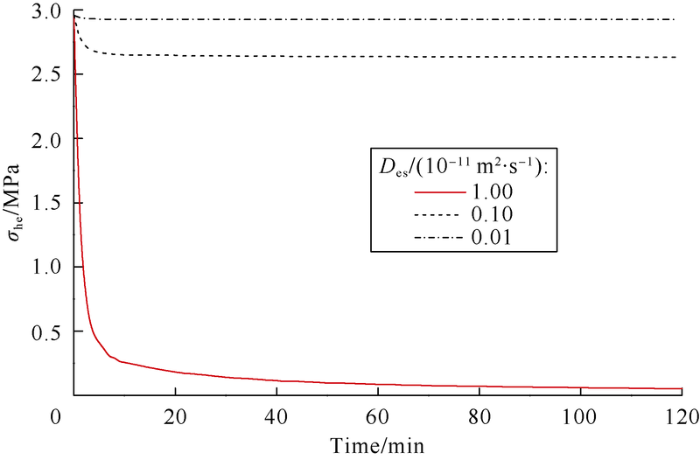
Fig. 8 shows the influence of diffusion coefficient on hydration swelling stress in shale (at hydration swelling coefficient ω0 of 2.0). Initially, no solute or water diffusion occurs. Although the diffusion coefficients are different, the hydration swelling stress is the same as the shale property and the solute concentrations on both sides are the same, thus the chemical potential differences on both sides are the same. Then, as time goes on, the hydration swelling stress decreases gradually and tends to be constant. 10 days later, the difference between hydration swelling stresses at Des=1×10-12 m2/s and Des= 1×10-13 m2/s is 0.31 MPa, while the difference between hydration swelling stresses at Des=1×10-11 m2/s and Des=1×10-12 m2/s is 2.58 MPa, which is about 8 times the former.
Fig. 8.
Influence of diffusition coefficient on hydration expansion pressure.
Fig. 9 shows the calculated results of shale strength damage at different diffusion coefficients and damage coefficients γ with m=1.5. It can be seen: (1) Rock strength damage is positively correlated with time, rises rapidly in the initial stage, and then slowly after inflection point occurring in about 1 day. (2) The greater the damage coefficient γ, the greater the strength damage is; and the damage coefficient will have stronger impact on the shale strength damage as time goes on. (3) When the diffusion coefficient decreases, as the solute transport and water diffusion turn slower, the hydration swelling strain decreases, and thus the resulted shale strength damage reduces.
Fig. 9.
Influence of sealing layer diffusion coefficient and damage coefficient on shale strength damage.
3.3. Influence of sealing, inhibition and inducing osmotic flow of drilling fluid on borehole wall safe drilling mud density window
According to the discussion above, the sealing and inducing osmotic flow performance of drilling fluid mainly influence the pore pressure transmission and solute diffusion at the borehole wall, which can be characterized by the permeability, diffusion coefficient and thickness of sealing layer. The thickness of sealing layer can be adjusted in a small range, and the thinner sealing layer is more tight and lower in permeability[2]. According to equation (17) and equation (21), permeability of the sealing layer is the major parameter that influence the pore pressure and solute concentration at the borehole wall. The inhibition performance of drilling fluid mainly affects the effective stress and shale strength damage at the borehole wall, which can be characterized by shale hydration swelling coefficient, residual hydration swelling pressure and damage coefficient. Therefore, the permeability, shale hydration swelling coefficient, strength damage coefficient and residual hydration swelling pressure of drilling fluid sealing layer are the main parameters influencing the safe drilling mud density window of shale borehole wall.
With the parameters in Table 1, setting ds=1 mm, σms= 1.5σm, m=1.5, and assuming that with the inhibition performance of drilling fluid improving, ω0, γ and αdπd decrease at the same time and at the same magnitude. The parameters combinations as shown in Table 3 were designed to calculate the safe drilling mud density window at different sealing performances (Ks), inhibition performances (ω0, γ, αdπd) and inducing osmosis flow performances (σms). The results are shown in Fig. 10.
Table 3 Parameter combinations used to calculate the safe drilling mud density window.
| Parameter combinations | Ks/ 10-10 μm2 | σm | ω0/ (MPa•mol-1•m3•s) | γ/ (m3•mol-1) | αdπd/ MPa |
|---|---|---|---|---|---|
| C1 | 1.0 | 0 | 0 | 0 | 0 |
| C2 | 1.0 | 0 | 1 | 0.005 | 0.5 |
| C3 | 1.0 | 0 | 2 | 0.010 | 1.0 |
| C4 | 1.0 | 0.2 | 0 | 0 | 0 |
| C5 | 1.0 | 0.2 | 1 | 0.005 | 0.5 |
| C6 | 1.0 | 0.2 | 2 | 0.010 | 1.0 |
| C7 | 0.1 | 0 | 0 | 0 | 0 |
| C8 | 0.1 | 0 | 1 | 0.005 | 0.5 |
| C9 | 0.1 | 0 | 2 | 0.010 | 1.0 |
| C10 | 0.1 | 0.2 | 0 | 0 | 0 |
| C11 | 0.1 | 0.2 | 1 | 0.005 | 0.5 |
| C12 | 0.1 | 0.2 | 2 | 0.010 | 1.0 |
| C13 | 0.1 | 0 | 0 | 0.010 | 1.0 |
| C14 | 0.1 | 0 | 1 | 0.010 | 1.0 |
| C15 | 0.1 | 0 | 2 | 0.010 | 0 |
| C16 | 0.1 | 0 | 2 | 0.010 | 0.5 |
Fig. 10.
Influence of permeability, shale hydration swelling coefficient, strength damage coefficient and residual hydration swelling pressure of sealing layer on shale borehole wall collapse pressure and fracturing pressure.
It can be known that: (1) The collapse pressure is positively correlated with the time, rises rapidly in the initial stage, and then rises slowly after the inflection point appears about 1 day later; the fracturing pressure is negatively correlated with time, decreases rapidly at first, and then decreases slowly after the inflection point occurs about 1 day later. (2) If the inhibition performance of drilling fluid is improved, ω0, γ and αdπd are reduced, the collapse pressure will reduce greatly, and the fracturing pressure will slightly increase. For example, when Ks=1.0×10-10 μm2, if there is no osmosis flow, with parameter combination C3 turning into parameter combinations C2 and C1, after 10 days, the safe drilling mud density window varies from no window (collapse pressure of 2.07 g/cm3, and the fracturing pressure of 1.98 g/cm3) to 1.56-2.01 g/cm3, and 1.10-2.03 g/cm3. (3) When the permeability of the sealing layer decreases, the collapse pressure decreases, and the fracturing pressure increases, widening the safe drilling mud density window. With the increase of collapse pressure equivalent density, the effect of sealing layer permeability on collapse pressure increases, and more reduction of the collapse pressure equivalent density will be induced with sealing layer permeability decreasing. For example, when the permeability of the sealing layer reduces from 1.0×10-10 μm2 to 1.0×10-11 μm2, if without osmotic flow, the safe drilling mud density window of 1.10-2.03 g/cm3 for the parameter combination C1 after 10 days would widen to 1.10-2.08 g/cm3 for parameter combination C7, and the safe drilling mud density window of parameter combination C3 would widen from no (collapse pressure being 2.07 g/cm3, fracturing pressure being 1.98 g/cm3) to 1.98 to 2.03 g/cm3. (4) If there is osmotic flow in shale, osmotic flow of fluid from shale to drilling fluid can reduce collapse pressure, and increase fracturing pressure, widening the window of safe drilling mud density. The lower the permeability of sealing layer, the greater its influence will be. For example, when sealing layer permeability is 1.0×10-10 μm2, under the influence of osmotic flow from shale to drilling fluid, the safe drilling mud density window (1.10-2.03g/cm3) of parameter combination C1 would widen to 1.09-2.04 g/cm3 of parameter combination C4 10 days later; when the sealing layer permeability is 0.1×10-10 μm2, under the influence of osmotic flow from shale to drilling fluid, the safe drilling mud density window (1.10-2.08 g/cm3) of parameter combination C7 would widen to 1.02-2.15 g/cm3 of parameter combination C10 after 10 days.
It can be seen that, for shale with significant strength damage due to hydration swelling, the improvement of drilling fluid inhibition can significantly reduce equivalent density of borehole wall collapse pressure. The improvement of drilling fluid sealing performance can reduce the permeability of sealing layer, reduce pore pressure transmission and solute diffusion, and thus prolong the collapse period and widen the window of safe drilling mud density. Moreover, the effecting magnitude of sealing layer permeability on collapse pressure equivalent density increases with the increase of collapse pressure equivalent density. Osmotic flow from shale into drilling fluid can reduce pore pressure and increase effective stress, thus making the collapse pressure equivalent density drop and the fracturing pressure equivalent density increase, and thus the window of safe drilling mud density widen. Moreover, the lower the sealing layer permeability, the greater the influence of osmotic flow on collapse pressure will be.
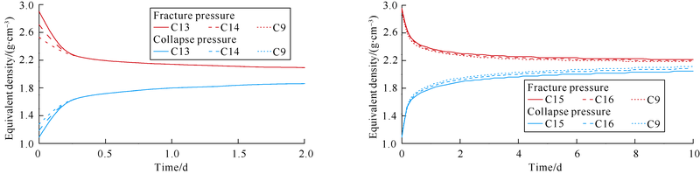
ω0, γ and αdπd are three parameters related to drilling fluid inhibition performance. When γ is kept unchanged ω0 is 0, 1, 2, αdπd is 0, 0.5, 1.0 MPa, Ks is 1.0×10-11 μm2, and there is no osmotic flow, the safe drilling mud density window is calculated, as shown in Fig. 11. It can be seen from the figure that: (1) The increase of ω0 causes the increase of collapse pressure and the decrease of fracturing pressure. With time going, the influence of ω0 variation on collapse pressure and fracturing pressure decreases gradually, and the influence can be ignored after 0.25 days. For example, with the increase of ω0, the initial safe drilling fluid density window for parameter combination C13 changes from 1.09-2.9 g/cm3 to 1.19-2.71 g/cm3 for parameter combination C14 and 1.28-2.53 g/cm3 for parameter combination C9, and the safe drilling mud density windows for parameter combination C13, C14 and C9 are the same 1.98-2.03 g/cm3 after 0.25 days. (2) The increase of αdπd results in the increase of collapse pressure and the decrease of fracturing pressure. For example, the safe drilling mud density window for parameter combination C15 of 1.94-2.05 g/cm3 changes into 1.96-2.04 g/cm3 for parameter combination C16 and 1.98-2.03 g/cm3 for parameter combination C9 10 days later. Compared with the effecting magnitude of drilling fluid inhibition performance (ω0, γ, αdπd) on collapse pressure equivalent density shown in Fig. 10, the change of ω0 and αdπd has smaller influence on the safe drilling mud density window. That is to say the decrease of shale strength damage (γ ) due to the improvement of drilling fluid inhibition performance is the decisive factor affecting collapse pressure equivalent density.
Fig. 11.
Influence of permeability, swelling coefficient and strength damage coefficient of sealing layer on collapse pressure and fracturing pressure at the borehole wall.
4. Conclusions
Improving drilling fluid sealing performance can reduce pore pressure transmission and solute diffusion at the borehole wall. The inhibition performance of drilling fluid, especially the inhibition to shale strength damage, is crucial to borehole wall collapse pressure for shale interval with significant hydration swelling property. Improving sealing and inhibition performance of drilling fluid can reduce collapse pressure and enhance fracturing pressure, and thus widen the safe drilling mud density window and prolong wellbore collapse time. The higher the collapse pressure, the higher the influence of drilling fluid sealing performance on it will be.
Osmotic flow of fluid from shale to drilling fluid can widen the safe drilling mud density window, and the better the drilling fluid sealing performance, the greater the influence of the osmotic flow on the safe drilling mud density window will be.
By modifying the generalized Biot effective stress equation and using Weibull statistical model to describe shale strength damage related to hydration strain, the method to calculate safe drilling mud density window has been established. The method can analyze the relationship between collapse pressure, fracturing pressure and anti-collapse performance of drilling fluid, and therefore can be used for accurate calculation of safe drilling mud density window and optimization of drilling fluid performance.
Nomenclature
a—constant, -24.6;
c—molar concentration of solute, mol/m3;
c0—initial molar concentration of solute in shale pore fluid, mol/m3;
cf—molar concentration of solute in drilling fluid, mol/m3;
cid—solute content in clay mineral spacing, mol/m3;
cip—molar concentration of solute in sink pore fluid, mol/m3;
cis—molar concentration of solute in source pore fluid, mol/m3;
ck—molar concentration of k component solute, mol/m3;
cs—molar concentration of solute in sealing layer pore fluid, mol/m3;
C—shale cohesion force, MPa;
Cac—average concentration of solute ions, mol/m3;
CsD—average concentration of solute, mol/m3;
d—clay mineral spacing, 0.1 nm;
ds—sealing layer thickness, mm;
D—hydration swelling damage, dimensionless;
Da—free diffusion coefficient of solute in pores, m2/s;
De—effective diffusion coefficient, m2/s;
Des—effective diffusion coefficient of solute in pores of sealing layer, m2/s;
Dm—total damage caused by hydration swelling and mechanical loading, dimensionless;
Dms—mechanical loading damage, dimensionless;
Ds—free diffusion coefficient of solute in water, m2/s;
g—gravitational acceleration, 9.8 m/s2;
GK—volume modulus of shale, MPa;
GKf—volume modulus of fluid, MPa;
GKm—volume modulus of shale matrix, MPa;
Gs—shear modulus of shale, MPa;
Jda—solute diffusion flux, mol/(m2•s);
i, j—component number;
k—solute component number;
K—permeability, 103 μm2;
Kh—flowing efficiency, m/s;
Ks—permeability of sealing layer, 103 μm2;
L—distance from borehole wall, m;
Lh—half-length of fracture, mm;
m—damage coefficient, dimensionless;
Ms—molar mass of solute, kg/mol;
p—pore pressure, MPa;
p0—initial pore pressure of shale, MPa;
pdf—drilling fluid column pressure, MPa;
ps—pore pressure of sealing layer, MPa;
r—distance from borehole center, m;
rw—wellbore radius, m;
R—universal gas constant, 8.314 J/ (mol•K);
t—time, s;
T—absolute temperature, K;
x—distance from fracture center in x direction, m;
α—Biot coefficient, dimensionless;
αd—correction coefficient of residual swelling pressure, dimensionless;
απ—diffusion correction coefficient, dimensionless;
γ—damage coefficient, m3/mol;
Δy(x)—fracture width at x, m;
δi,j—coefficient with value 1 when i=j, and with value 0 when i≠j, dimensionless;
${{\varepsilon }_{\text{v0,chem}}}$—average hydration swelling volume strain, dimensionless;
${{\varepsilon }_{\text{v,chem}}}$—hydration swelling volume strain, dimensionless;
η—drilling fluid viscosity, mPa•s;
μ—chemical potential, J/mol;
μk—chemical potential of k component of pore fluid, J/mol;
ν—Poisson's ratio, dimensionless;
πd—residual hydration swelling pressure in clay spacing, MPa;
${{\rho }_{\text{f}}}$—drilling fluid density, kg/m3;
${{\rho }_{\text{w}}}$—water density, kg/m3;
${{\sigma }_{\text{c}}}$—confining pressure, MPa;
${{\sigma }_{\text{e,}i\text{,}j}}$—component of effective stress, MPa;
${{\sigma }_{\text{h}}}$—minimum horizontal stress, MPa;
${{\sigma }_{\text{he}}}$—hydration stress, MPa;
${{\sigma }_{\text{hf}}}$—hydration swelling pressure in fracture, MPa;
${{\sigma }_{\text{H}}}$—maximum horizontal stress, MPa;
${{\sigma }_{i\text{,}j}}$—component of stress tensor, MPa;
${{\sigma }_{\text{m}}}$—shale membrane efficiency, dimensionless;
${{\sigma }_{\text{ms}}}$—sealing layer membrane efficiency, dimensionless;
${{\sigma }_{\text{t}}}$—tensile strength, MPa;
${{\sigma }_{\text{v}}}$—overburden pressure, MPa;
$\sigma _{1}^{*}$—maximum principal effective stress, MPa;
$\sigma _{3}^{*}$—minimum principal effective stress, MPa;
$\sigma _{i\text{,}j}^{*}$—effective stress considering strength damage, MPa;
τ—geometric characteristic parameter of pore, dimensionless;
ϕ—porosity, %;
${{\phi }_{\text{s}}}$—sealing layer porosity, %;
φ—internal friction angle of shale, (°);
ω—osmotic efficiency in clay spacing, dimensionless;
${{\omega }_{\text{0}}}$—hydration swelling coefficient related to solute concentration variation, MPa•s•m3/mol;
${{\omega }_{\text{1}}}$—damage coefficient related to solute concentration, m3/mol;
${{\omega }_{k}}$—hydration swelling coefficient related to chemical potential of k component, MPa•mol/J;
${{\omega }_{\text{k0}}}$—hydration swelling coefficient related to chemical potential of single component, MPa•mol/J.
Reference
A wellbore stability analysis model with chemical-mechanical coupling for shale gas reservoirs
DOI:10.1016/j.jngse.2015.05.028 URL [Cited within: 1]
Monte Carlo estimation on the parameters of shale chemo- poro-mechanical coupling model
A multivariate cooperation principle for well-bore stabilization
Estimation of montmorillonite swelling pressure: A molecular dynamics approach
DOI:10.1021/acs.jpcc.5b04972 URL [Cited within: 1]
Quantitative characterization of micro forces in shale hydration and field applications
Effects of hydration on the microstructure and physical properties of shale
DOI:10.1016/S1876-3804(18)30110-1 URL [Cited within: 1]
Hydration swelling of water- absorbing rocks: A constitutive model
DOI:10.1002/(ISSN)1096-9853 URL [Cited within: 7]
Influence of coupled chemo-poro-thermoelastic processes on pore pressure and stress distributions around a wellbore in swelling shale
DOI:10.1016/j.petrol.2009.02.015 URL [Cited within: 2]
Finite element analysis of coupled chemo-poro-thermo-mechanical effects around a wellbore in swelling shale
DOI:10.1073/pnas.1808402115
URL
PMID:30442660
[Cited within: 3]

Organic matter is responsible for the generation of hydrocarbons during the thermal maturation of source rock formation. This geochemical process engenders a network of organic hosted pores that governs the flow of hydrocarbons from the organic matter to fractures created during the stimulation of production wells. Therefore, it can be reasonably assumed that predictions of potentially recoverable confined hydrocarbons depend on the geometry of this pore network. Here, we analyze mesoscale structures of three organic porous networks at different thermal maturities. We use electron tomography with subnanometric resolution to characterize their morphology and topology. Our 3D reconstructions confirm the formation of nanopores and reveal increasingly tortuous and connected pore networks in the process of thermal maturation. We then turn the binarized reconstructions into lattice models including information from atomistic simulations to derive mechanical and confined fluid transport properties. Specifically, we highlight the influence of adsorbed fluids on the elastic response. The resulting elastic energy concentrations are localized at the vicinity of macropores at low maturity whereas these concentrations present more homogeneous distributions at higher thermal maturities, due to pores' topology. The lattice models finally allow us to capture the effect of sorption on diffusion mechanisms with a sole input of network geometry. Eventually, we corroborate the dominant impact of diffusion occurring within the connected nanopores, which constitute the limiting factor of confined hydrocarbon transport in source rocks.
Effects of salinity and confining pressure on hydration-induced fracture propagation and permeability of Mancos shale
DOI:10.1007/s00603-017-1278-z URL [Cited within: 5]
Effect of water imbibition on fracture generation in mancos shale under isotropic and anisotropic stress conditions
A novel experimental technique to monitor the time-dependent water and ions uptake when shale interacts with aqueous solutions
DOI:10.1007/s00603-012-0327-x
URL
[Cited within: 2]

The time-dependent water and ions uptake when shale interacts with aqueous solutions is quantified using a combination of immersion and gravimetric techniques. Results show that when shale interacts with salt solutions, water uptake into shale goes through three distinct stages; water movement out of shale (due to chemical osmosis), water movement into shale (due to diffusion osmosis) and stationary state (equilibrium stage). This work shows that chemical osmosis dominates water movement in early times while diffusion osmosis takes over later. In addition, it is shown that the amount of water movement due to chemical osmosis depends on the chemical potential gradient while the amount of water movement due to diffusion osmosis is highly related to the ionic concentration imbalance. In addition, the amount of ions uptake into shale at equilibrium is shown to depend on the type and concentration of salt solution. Furthermore, this work shows that potassium ion has a strengthening effect on shale while sodium and calcium ions have a weakening effect on shale. Results also show that the shale’s compressive strength alteration is greatly influenced by the type and concentration of the salt solution. Furthermore, the shale’s compressive strength alteration is shown to be time dependent and correlates very well with the time-dependent flux of water and ions. Finally, it is shown that chemical osmosis and diffusion osmosis take place simultaneously when shale interacts with water-based muds. The overall impact on shale stability is governed by the net water flow resulting from chemical osmosis and diffusion osmosis.
Experimental study on anisotropic strength and deformation behavior of a coal measure shale under room dried and water saturated conditions
Swelling and softening behavior of La Biche shale
DOI:10.1139/t97-087 URL [Cited within: 3]
Connecting the molecular scale to the continuum scale for diffusion processes in smectite-rich porous media
DOI:10.1016/j.foodchem.2019.125999
URL
PMID:31864185
[Cited within: 2]

A method based on solid-phase extraction (SPE) coupled with high-performance liquid chromatography (HPLC) was developed to determine the content of 4-chlorophenoxy acetic acid (PCPA), naphthylacetic acid (NAA) and 2,4-dichlorophenoxyacetic acid (2,4-D) in green bell peppers. A molecularly imprinted 3-aminophenol-glyoxal-urea resin (MIAGUR) was first synthesized as a specific SPE adsorbent, which exhibited special selectivity and multiple adsorption interactions including hydrogen bonding and π-π interactions. The quantities of PCPA, NAA and 2,4-D in green bell peppers from 20 samples scattered throughout Baoding city (Hebei province, China) were determined using the proposed method. The results suggested that the use of PCPA, NAA and 2,4-D in green bell peppers from Baoding's markets is almost in fair. Moreover, MIAGUR-SPE-HPLC is suitable for the specific simultaneous monitoring of PCPA, NAA, and 2,4-D in green bell peppers and has potential applications in determination of PCPA, NAA, and 2,4-D of other plant products.
Compressibility behavior of clays at large pressures
DOI:10.1139/t06-123 URL [Cited within: 1]
Effect of montmorillonite content and sodium chloride solution on the residual swelling pressure of an expansive clay
DOI:10.1007/s12665-017-7169-5 URL [Cited within: 2]
Diffusion-driven transport in clayrock formations
DOI:10.1016/j.apgeochem.2011.09.015
URL
[Cited within: 2]

Clay mineral-rich sedimentary formations are currently under investigation to evaluate their potential use as host formations for installation of deep underground disposal facilities for radioactive waste (e.g. Boom Clay (BE), Opalinus Clay (CH), Callovo-Oxfordian argillite (FR)). The ultimate safety of the corresponding repository concepts depends largely on the capacity of the host formation to limit the flux towards the biosphere of radionuclides (RN) contained in the waste to acceptably low levels. Data for diffusion-driven transfer in these formations shows extreme differences in the measured or modelled behaviour for various radionuclides, e. g. between halogen RN (Cl-36, I-129) and actinides (U-238,U-235, Np-237, Th-232, etc.), which result from major differences between RN of the effects on transport of two phenomena: diffusion and sorption. This paper describes recent research aimed at improving understanding of these two phenomena, focusing on the results of studies carried out during the EC Funmig IP on clayrocks from the above three formations and from the Boda formation (HU).
Project results regarding phenomena governing water, cation and anion distribution and mobility in the pore volumes influenced by the negatively-charged surfaces of clay minerals show a convergence of the modelling results for behaviour at the molecular scale and descriptions based on electrical double layer models. Transport models exist which couple ion distribution relative to the clay-solution interface and differentiated diffusive characteristics. These codes are able to reproduce the main trends in behaviour observed experimentally, e.g. D-e(anion) < D-e(HTO) < D-e(cation) and D-e(anion) variations as a function of ionic strength and material density. These trends are also well-explained by models of transport through ideal porous matrices made up of a charged surface material. Experimental validation of these models is good as regards monovalent alkaline cations, in progress for divalent electrostatically-interacting cations (e.g. Sr2+) and still relatively poor for 'strongly sorbing', high K-d cations.
Funmig results have clarified understanding of how clayrock mineral composition, and the corresponding organisation of mineral grain assemblages and their associated porosity, can affect mobile solute (anions, HTO) diffusion at different scales (mm to geological formation). In particular, advances made in the capacity to map clayrock mineral grain-porosity organisation at high resolution provide additional elements for understanding diffusion anisotropy and for relating diffusion characteristics measured at different scales. On the other hand, the results of studies focusing on evaluating the potential effects of heterogeneity on mobile species diffusion at the formation scale tend to show that there is a minimal effect when compared to a homogeneous property model. Finally, the results of a natural tracer-based study carried out on the Opalinus Clay formation increase confidence in the use of diffusion parameters measured on laboratory scale samples for predicting diffusion over geological time-space scales.
Much effort was placed on improving understanding of coupled sorption-diffusion phenomena for sorbing cations in clayrocks. Results regarding sorption equilibrium in dispersed and compacted materials for weakly to moderately sorbing cations (Sr2+, Cs+, Co2+) tend to show that the same sorption model probably holds in both systems. It was not possible to demonstrate this for highly sorbing elements such as Eu(III) because of the extremely long times needed to reach equilibrium conditions, but there does not seem to be any clear reason why such elements should not have similar behaviour. Diffusion experiments carried out with Sr2+, Cs+ and Eu(III) on all of the clayrocks gave mixed results and tend to show that coupled diffusion-sorption migration is much more complex than expected, leading generally to greater mobility than that predicted by coupling a batch-determined K-d and Ficks law based on the diffusion behaviour of HTO. If the K-d measured on equivalent dispersed systems holds as was shown to be the case for Sr, Cs (and probably Co) for Opalinus Clay, these results indicate that these cations have a D-e value higher than HTO (up to a factor of 10 for Cs+). Results are as yet very limited for very moderate to strongly sorbing species (e.g. Co(II), Eu(III), Cu(II)) because of their very slow transfer characteristics. (C) 2011 Elsevier Ltd.
Coupling effects during steady-state solute diffusion through a semipermeable clay membrane
DOI:10.1016/j.foodchem.2019.125999
URL
PMID:31864185
[Cited within: 1]

A method based on solid-phase extraction (SPE) coupled with high-performance liquid chromatography (HPLC) was developed to determine the content of 4-chlorophenoxy acetic acid (PCPA), naphthylacetic acid (NAA) and 2,4-dichlorophenoxyacetic acid (2,4-D) in green bell peppers. A molecularly imprinted 3-aminophenol-glyoxal-urea resin (MIAGUR) was first synthesized as a specific SPE adsorbent, which exhibited special selectivity and multiple adsorption interactions including hydrogen bonding and π-π interactions. The quantities of PCPA, NAA and 2,4-D in green bell peppers from 20 samples scattered throughout Baoding city (Hebei province, China) were determined using the proposed method. The results suggested that the use of PCPA, NAA and 2,4-D in green bell peppers from Baoding's markets is almost in fair. Moreover, MIAGUR-SPE-HPLC is suitable for the specific simultaneous monitoring of PCPA, NAA, and 2,4-D in green bell peppers and has potential applications in determination of PCPA, NAA, and 2,4-D of other plant products.
On statistical damage constitutive model and its parameters for rock based on normal distribution
DOI:10.13227/j.hjkx.201907016
URL
PMID:31854947
[Cited within: 1]

We use 3487 surface soil samples, 35 soil profile samples, and 93 agricultural products and root soil samples obtained from the southeastern Tarim basin, Xinjiang, northwestern China (Ruoqiang County and Qiemo County, Bayingguo Mongolia Autonomous Prefecture, and Minfeng County and Yutian County, Hetian Prefecture) to assess As contamination. Multivariate statistical analysis, geostatistics, and global information system (GIS) techniques are used to study:the spatial distribution characteristics of soil As, the effects of various agricultural products on As enrichment, and to compare the characteristics of the As content of agricultural products and root soils in spatially significantly and non-significantly autocorrelated regions. The As content of soil samples were relatively low, and the average As contents determined for agricultural land and non-agricultural land were 9.81 mg·kg-1 and 7.94 mg·kg-1, respectively. We found that 568 surface soil samples (16.3% of all samples) had an As content that exceeded Xinjiang soil background values (11.2 mg·kg-1) and that five samples exceeded the risk screening values (25 mg·kg-1). The Moran's indexes of spatial autocorrelation were>0, and the main aggregation types of spatial autocorrelation of soil As were high-high and low-low types, with the zone of the high-high type being mainly located in the agricultural land of each county. A GIS spatial distribution map showed that the high value area of soil As content presented a flaky or island-like scattered distribution. The standard deviation ellipses showed that the trend direction of soil As content in:Ruoqiang County was from north to south, Qiemo County and Minfeng County were both from southwest to northeast, and Yutian County was from northwest to southeast. The As content of the vertical profiles of the agricultural land in Ruoqiang County fluctuated from the surface to depth, whereas those of other counties were relatively stable. The As enrichment ability of crops was ranked as:root vegetables > walnuts > wheat > corn > red dates. The As contents of corn and red dates showed a significant positive correlation with that of the root soil. There was no significant difference in the As content of agricultural products between significant autocorrelation zones and non-significant autocorrelation zones, whereas there was a significant difference in the As content of root soils.
Study on damage constitutive model of rocks based on lognormal distribution
DOI:10.1016/j.chemosphere.2019.125591
URL
PMID:31864066
[Cited within: 1]

The level of concentration of heavy metal (loids) in tobacco-growing soils is detrimental to soil quality. In this study, 256 topsoil samples were collected from Zunyi city to understand the concentration, spatial distribution characteristics, sources and health risks of heavy metal (loids) by using mathematical statistics, geostatistical analyst, and conditional inference tree (CIT). The results showed that the average contents of Hg, Pb, Zn, and Cd in tobacco-growing soils were high with 1.7, 1.2, 1.1 and 1 times the background value, respectively. While, Ni, Cr, Cu and As were temporarily within the permissible limits. Concentrations of Hg, Cd, Pb, and Zn in the soils of Wuchuan, Tongzi, Daozhen, and Yuqing were much higher than the other regions due to human activities. According to the CIT, the main nodes were 1) distance from sampling to the main road, 2) organic matter, 3) factories, and 4) soil types. The results indicated that for Pb and Zn, the sources of pollution might be transportation; for Cu, As, and Cd, the sources were utilization of phosphate, tobacco-specific fertilizers, and organic fertilizers; and the sources of Hg were coal combustion and metals smelting. In addition, high background values of heavy metal (loids) in karst landforms were responsible for the accumulation of Cd. With respect to Hazard Quotient and Lifelong Carcinogenic Risk, the exposed individual was unlikely to experience obvious adverse health effect due to the heavy metal (loids) pollution, except Cr, which should be particularly considered in further risk control.
A statistical damage softening constitutive model for rock and back analysis of its parameters
A damage-softening statistical constitutive model considering rock residual strength
DOI:10.1016/j.cageo.2006.02.011
URL
[Cited within: 3]

Abstract
Under stress, the microcracks in rock evolve (initiation, growth and coalescence) from damage to fracture with a continuous process. In order to describe this continuous process, a damage-softening statistical constitutive model for rock was proposed based on the Weibull distribution of mesoscopic element strength. This model usually adopts the Drucker–Prager criterion as its distribution parameter of mesoscopic element strength, which may produce larger damage zone in numerical simulations. This paper mainly studies the effects of strength criteria and residual strength on the performance of this damage-softening statistical constitutive model of rock. Main works include following three aspects: Firstly, the mechanical behaviors of rock are comparatively studied when the Drucker–Prager and the Mohr–Coulomb criteria are employed, respectively, as the distribution parameter. Then, a coefficient is introduced to make this constitutive model be capable of describing the residual strength of rock. Finally, a user-defined subroutine is concisely developed for this model and checked through typical strain paths. The current work lays a good foundation for further application of this model in geotechnics and geosciences.
A statistical distribution function of wide applicability
DOI:10.1016/j.addbeh.2018.12.018
URL
PMID:30639230
[Cited within: 2]

A risk factor or intervention (an independent variable) may influence a substance abuse outcome (the dependent variable) indirectly, by affecting an intervening variable (a mediator) that in turn affects that outcome. Mediation analysis is a statistical method commonly used to examine the interrelations among independent, mediating, and dependent variables to obtain the direct and indirect effects of an independent variable on a continuous dependent variable. However, mediation analysis may also be used with binary outcomes, such as a diagnosis of an alcohol use disorder (AUD). Study 1 demonstrated methods of mediation analysis with binary outcomes by examining the direct and indirect effects of pro-alcohol social influences on an AUD, as a function of: (a) the distribution of the independent variable (binary vs. continuous), (b) the frequency of the outcome (non-rare vs. rare), and (c) the effect metric (probability vs. odds ratio). Study 2 was a Monte Carlo (simulation) study of bias in the indirect effects based on estimates from the first study. These methods have wide applicability in addictions research because many key outcomes are binary, and mediation analysis is frequently used to study the causal mechanisms by which interventions and risk factors affect substance abuse.
Damage model of rock under temperature and load
A course on damage mechanics. 2nd ed
DOI:10.3390/jcm8112008
URL
PMID:31744243
[Cited within: 1]

Extremely low-frequency pulsed electromagnetic field (ELF-PEMF) therapy is proposed to support bone healing after injuries and surgical procedures, being of special interest for elderly patients. This study aimed at investigating the effect of a specific ELF-PEMF, recently identified to support osteoblast function in vitro, on bone healing after high tibial osteotomy (HTO). Patients who underwent HTO were randomized to ELF-PEMF or placebo treatment, both applied by optically identical external devices 7 min per day for 30 days following surgery. Osseous consolidation was evaluated by post-surgical X-rays (7 and 14 weeks). Serum markers were quantified by ELISA. Data were compared by a two-sided t-test (α = 0.05). Device readouts showed excellent therapy compliance. Baseline parameters, including age, sex, body mass index, wedge height and blood cell count, were comparable between both groups. X-rays revealed faster osseous consolidation for ELF-PEMF compared to placebo treatment, which was significant in patients ≥50 years (∆mean = 0.68%/week; p = 0.003). Findings are supported by post-surgically increased bone-specific alkaline phosphatase serum levels following ELF-PEMF, compared to placebo (∆mean = 2.2 µg/L; p = 0.029) treatment. Adverse device effects were not reported. ELF-PEMF treatment showed a tendency to accelerate osseous consolidation after HTO. This effect was stronger and more significant for patients ≥50 years. This ELF-PEMF treatment might represent a promising adjunct to conventional therapy supporting osseous consolidation in elderly patients.
A permeability-porosity relationship for mudstones
DOI:10.1016/j.marpetgeo.2009.07.001
URL

Abstract
The relationship between permeability and porosity for fine-grained clastic sediments (“mudstones”) is a key constitutive equation for modelling subsurface fluid flow and is fundamental to the quantification of a range of geological processes. For a given porosity, mudstone permeability varies over a range of 2–5 orders of magnitude. We show here that much of the range can be explained by variations in lithology, which we define simply and pragmatically by clay content (mass fraction of particles less than 2 microns in diameter). Using clay content as the quantitative lithology descriptor, we have used a dataset (clay content range of 12–97%; porosity range of 0.04–0.78; six orders of magnitude permeability range) comprising 376 data points to derive a new bedding perpendicular permeability (K, m2) – void ratio (e = porosity/(1-porosity)) relationship as a function of clay content (CF):
ln(K)=−69.59−26.79⋅CF+44.07⋅CF0.5+(−53.61−80.03⋅CF+132.78⋅CF0.5)⋅?+(86.61+81.91⋅CF−163.61⋅CF0.5)⋅?0.5The coefficient of regression (r2) = 0.93. At a given porosity, the inclusion of the quantitative lithological descriptor, clay content reduces the predicted range of permeability from 2 to 5 orders of magnitude to one order.
Diffusion and retention of sodium and strontium in opalinus clay: Comparison of sorption data from diffusion and batch sorption measurements, and geochemical calculations
DOI:10.1016/j.apgeochem.2005.08.008
URL

Abstract
The retention of 22Na and 85Sr on Opalinus clay from Benken and the Mont Terri Rock Laboratory (Switzerland) was measured by through- and out-diffusion measurements on intact rock samples, and by batch sorption on crushed material. The sorption values obtained from these measurements were compared with one another and with ones calculated from a selectivity coefficient/geochemical modelling approach. One of the main aims of the work was to test to what extent sorption values deduced from diffusion experiments on intact rock were compatible with those measured in batch tests on crushed material and with sorption values calculated from geochemical modelling. This is an important consideration in repository performance assessment studies because apparent diffusion coefficients are often calculated from batch Rd values and effective diffusion coefficients measured using tritiated water.
In general, there was excellent agreement between the distribution ratios for Na obtained by all 3 approaches for both sources of Opalinus clay. For Sr the agreement was also good, but the calculations based on selectivity coefficients in the case of Benken, and the batch sorption data in the case of Mont Terri material were a factor of ∼2 different from the values found in the other two cases. Nevertheless, a factor of ∼2 difference in the worst case is not considered to be significant when the errors associated with the different methods are considered realistically.
The uptake mechanism for both elements in the Opalinus clay system is cation exchange and the results strongly indicate that there is no significant difference between the exchange capacity available in the dispersed and in the intact rock systems i.e. reduced site accessibility in intact Opalinus clay is not an issue where sorption by cation exchange is occurring.
Diffusion experiments in Callovo-Oxfordian clay from the Meuse/Haute-Marne URL, France. Experimental setup and data analyses
DOI:10.1016/j.clinimag.2019.11.005
URL
PMID:31864206

Male breast cancer is a rare malignancy. Due to low prevalence and limited data to support male breast cancer screening, there are currently no recommendations for image-based screening in asymptomatic men and few recommendations for men at high risk for breast cancer. However, symptomatically diagnosed cancers in men are typically advanced, suggesting that earlier detection may improve outcomes. In this article we briefly review the risk factors for male breast cancer, and discuss the potential benefits and possible drawbacks of routine image-based screening for men at high risk for breast cancer.