Introduction
In petroleum basins, salt bodies are closely related to oil and gas migration, accumulation, storage, exploration, and development[1,2,3]. About 80% of the petroleum-bearing basins in the world are salt basins[4] and contain a large amount of the world’s hydrocarbon reservoirs. Gypsum-salt strata are generally not primary drilling targets but their very low permeability properties[5] serve as ideal caprocks for hydrocarbon reservoirs, and large oil and gas fields are often hidden under the thick salt layers, such as in the Gulf of Mexico basin, the West Africa basins, and off-shore Brazil[6]. However, the mechanical properties of salt are relatively unique compared with the surrounding sediments and characterized by low mechanical strength, low-activation creep, and plastic deformation[5,7,8]. The stresses and pore-fluid pressure around a salt body will therefore be disturbed under equilibrant action during viscoelastic stress relaxation.
Drilling in gypsum-salt strata is prone to engineering accidents, especially in deep operations, owing to the perturbations of formation stress and pore pressure, such as wellbore instability, sticking, and casing collapse[9]. Previous studies have used geomechanical methods to model salt basins (e.g., evolution model, static model) and simulate the stress perturbations around a salt body[10,11]. Salt body geometry has an important influence on the stress perturbations[12,13,14,15,16]; however, the relationship between the regional background stress field pattern (i.e., compression vs. tension), geometry of the salt body (e.g., protrusions or depressions) and stress perturbations are not easily predicted using such models. In this paper, we build a static model under compressional stress to calculate the stress change around a salt basin. We analyze the mode of stress perturbation caused by different salt body geometries and test the effect of salt fluctuation on the stress perturbation magnitude. We performed simulations of a salt deposit in the western Kelasu section of the Kuqa depression in the Tarim Basin of western China. The results of this study provide a scientific basis for the prediction of stress perturbation and well design in compressional salt basin systems.
1. Overview of the study area
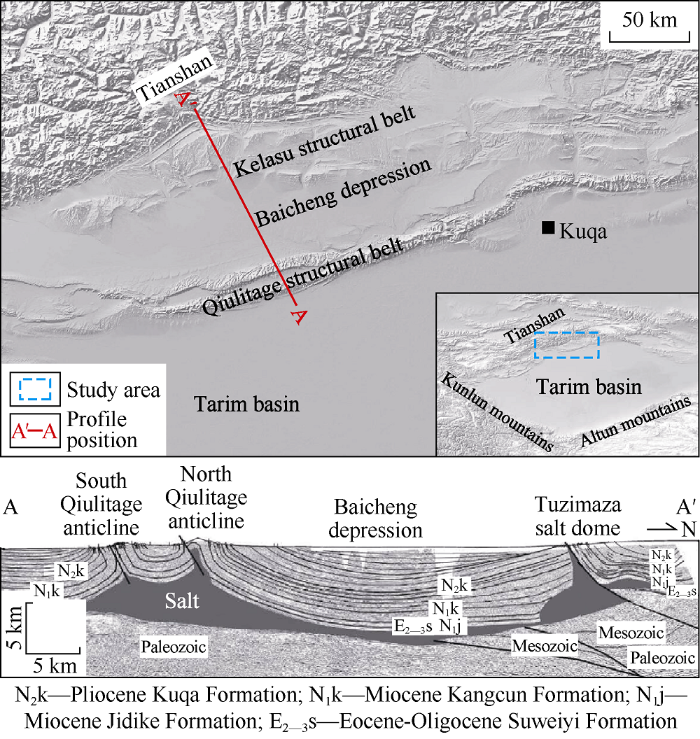
The Kuqa depression between the Tabei uplift and the South Tianshan orogenic belt which is located in the north of the Tarim Basin, and extends from Wensu in the west to Korla in the east[17]. It has a width of 20-100 km from north to south, and the length of about 500 km from east to west[18]. A thick gypsum-salt formation was deposited in the Kuqa depression during the Tertiary[19], and various types of salt structures formed owing to the strong compression of the middle-late Himalayan movement and difference in overburden loading[20]. The salt structure in this area consists of three parts, which are from bottom to top presalt sediments, salt layer and sediments overlying salt (postsalt sediments)[21].
The study area is located in the western of Kelasu structural belt in the Kuqa depression with a north-south horizontal length of 76 km and a depth of 15 km. Salt diapir structures are developed on the north and south sides of the Baicheng depression, and faults are developed on the north side of the Tuzimaza salt dome. The South Qiulitage anticline and the North Qiulitage anticline are two closed box folds that are located on the salt dome. The thicknesses of salt and the overlying stratum of Baicheng depression are 5-7 km and 6-7 km, respectively (Fig. 1).
Fig. 1.
Fig. 1.
The main geological structures and the seismic profile to the west of Kelasu structural belt in Kuqa depression, the northern margin of Tarim Basin[17].
The salt in the study area is a typical compressional salt structure[22,23,24,25,26]. According to multiparameter measurements and interpretation of the formation rock magnetic fabric, hydraulic fracturing, and well diameter caving, the maximum principal compressive stress direction of the current stress field in the Kuqa depression is nearly north-south[27]. According to the development of thrust faults in the Triassic Karamay formation sandstones in the Kuqa depression, we can assess that the middle principal stress directions of the structural stress field in the Kuqa depression is nearly east-west, and the minimum principal stress is vertical[28].
2. Model setup
Single-layer, double-layer, or multi-layer salt structures are common in nature, such as the Balingshan-Huayuan multi-layer salt structure in the Jiangling Sag, Jianghan Basin, the salt structure in the Lanping Basin, West Yunnan, and the salt structure in the north-central Gulf of Mexico[29,30,31]. In this paper, we construct a double-layer salt structure model in addition to a single-layer model. The results are consistent with conclusions regarding the double-layer salt structure model and relationship between stress perturbation and salt geometry. We use commercial software to establish a two-dimensional plane strain finite element model[32] (Fig. 2), which assumes that the salt is a Maxwell linear viscoelastic body[33] and the sediment is an elastic solid (i.e., with no pore pressure). The salt body is assumed to be impermeable[13] and there is no pore pressure. The material parameters of the model are shown in Table 1.
Fig. 2.
Fig. 2.
Finite element mesh and boundary conditions.
Table 1 Material parameters of the finite element model.
The model in this study has a simulation depth of 20 km and a horizontal width of 45 km. There are two salt layers in the model, corresponding to the three types of salt geometries: the salt bodies with protuberances on the left side, salt bodies with bulge and sag combination in the middle, and the salt bodies with depressions on the right side. The average depth of the upper and lower salt bodies is about 6.5 km, 15.0 km, respectively. Both the left, right and the bottom boundary of the model are slip boundaries: The bottom boundary has only horizontal displacement and no vertical displacement; whereas the left and right boundaries have only vertical displacement and no horizontal displacement. The upper boundary is a free boundary. The finite element mesh near the salt body is encrypted to better show the stress perturbations near the salt body.
The static mechanical equilibrium equation of the model is:
where, $\partial \sigma_{ij}$is the stress tensor (i, j = 1, 2, 3), $\rho g_{i}$is the physical item. In this study, the compressive stress is positive.
The increase in strain at each step of the model is expressed as:
where, $\sigma^{t}$is the stress increment at time t, {dσ} and dt are the stress tensor increment and time increment respectively, Q is the viscosity related matrix, D is the elastic material matrix.
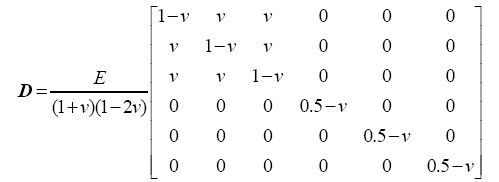
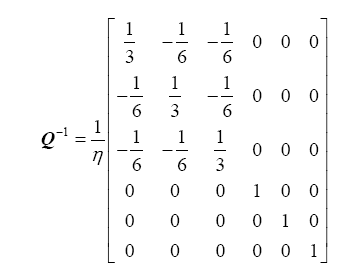
For the background stress field of the model, the vertical stress ($\sigma_{v}$) of the model is set as the minimum principal stress ($\sigma_{3}$), and the horizontal stress and the normal stress ($\sigma_{h},\sigma_{ooo}$) correspond to the maximum principal stress $\sigma_{1}$ and the intermediate principal stress $\sigma_{2}$ respectively. The initial vertical stress is equal to the integral of the gravity of the overlying strata with depth. Under the compressional stress field, the horizontal stress is set at 1.3 times of the vertical stress, and the normal stress is set at 1.1 times of the vertical stress:
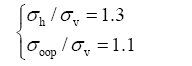
3. Modeling results
3.1. Reference model
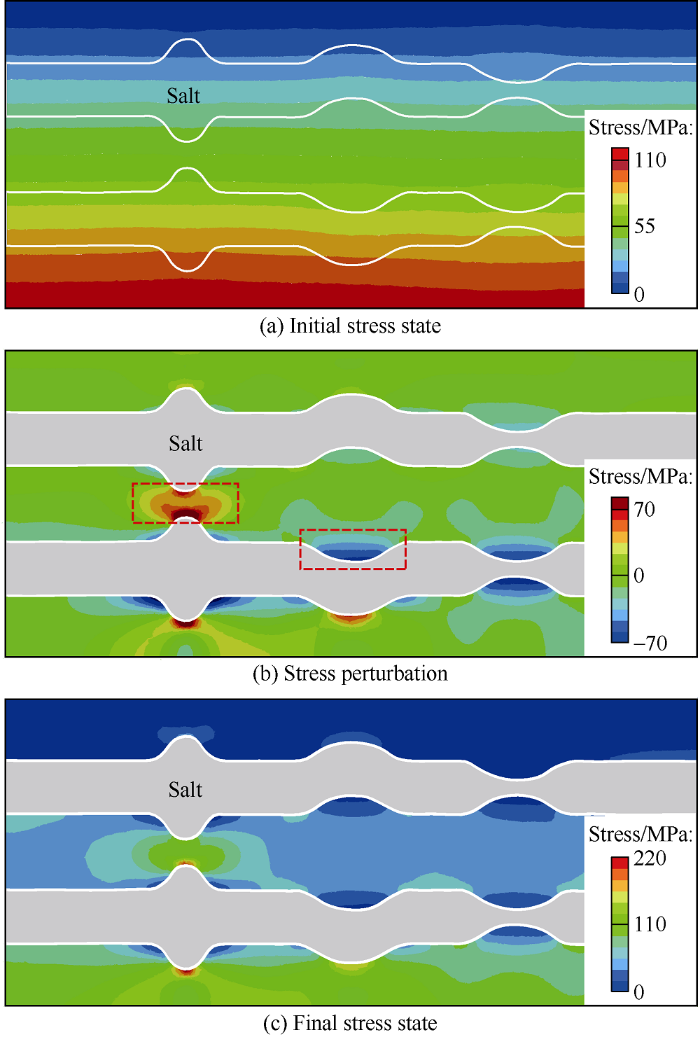
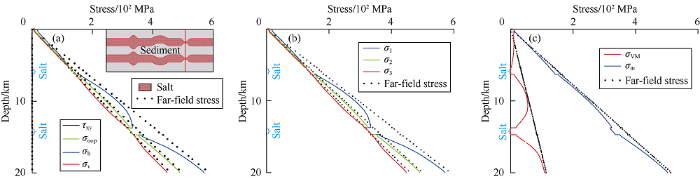
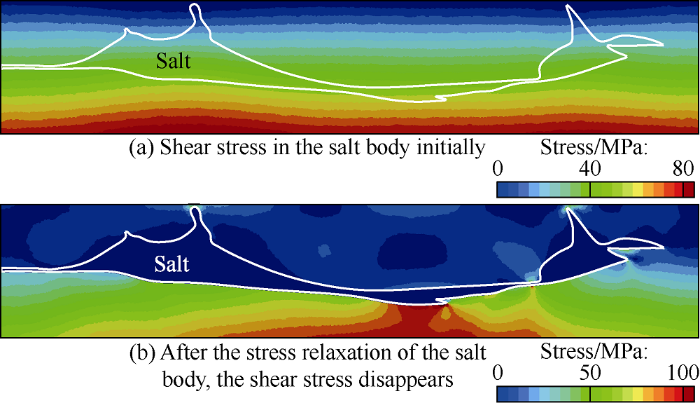
We assume that the initial stresses in the vertical, horizontal, and out-of-plane directions increase with depth, so the initial von Mises (shear stresses in three dimensions, see equation (8)) stress also increases with depth (Fig. 3a). As the viscoelastic salt cannot bear the deviatoric stress[12], the shear stress in the salt gradually relaxes and decreases with time, and stress perturbations are generated in the sediment around the salt body (Fig. 3b). The final stress state of the model (Fig. 3c) is the sum of the initial state stress (Fig. 3a) and the stress perturbation caused by the viscoelastic stress relaxation of the salt (Fig. 3b). The compressive stress is positive in this study.
Fig. 3.
Fig. 3.
von Mises stress in different states of reference model.
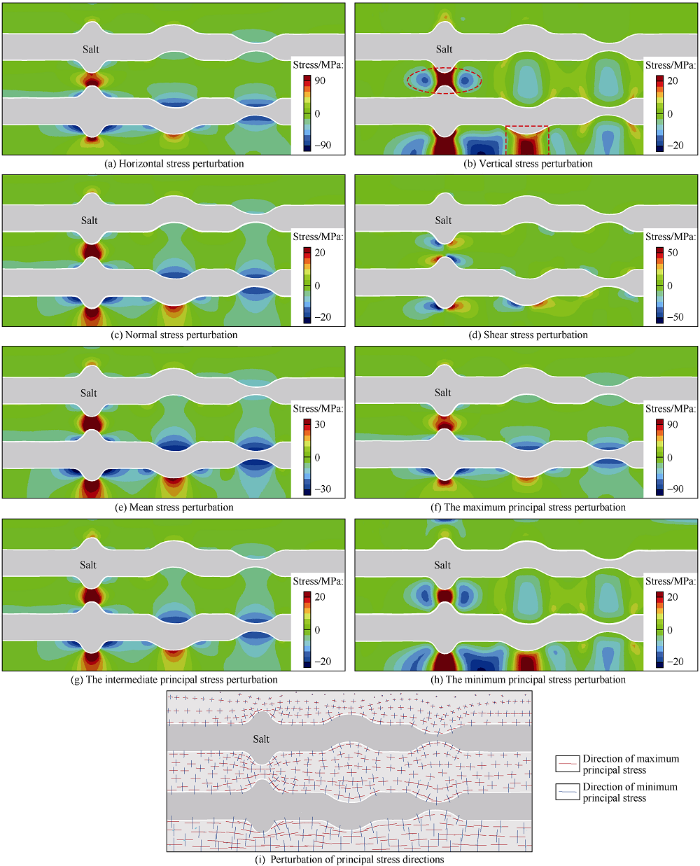
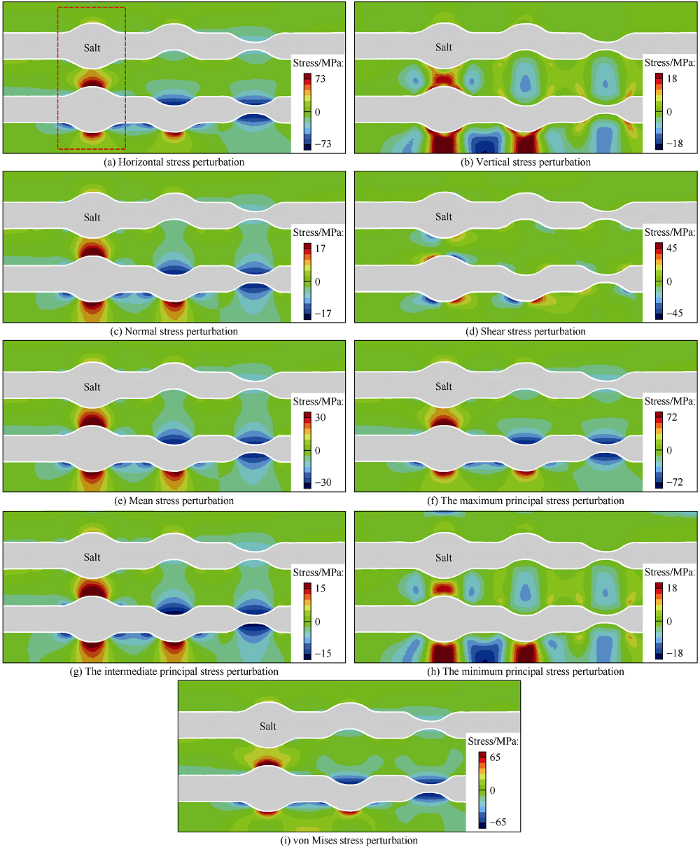
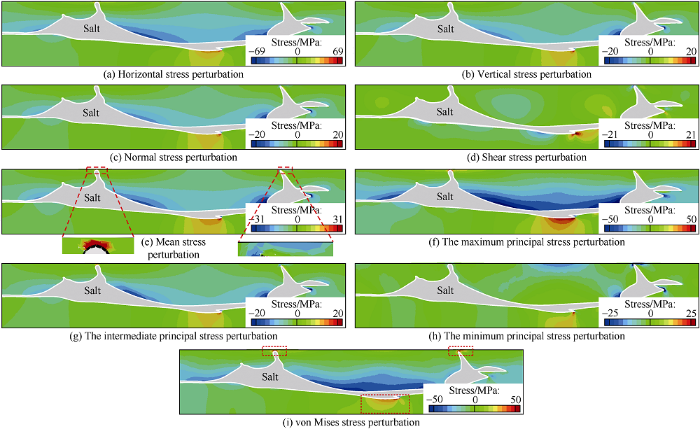
In the model, the horizontal stress, vertical stress, and out-of-plane stress gradually increase at the salt protrusions (Fig. 4a-4c). Both the horizontal and out-of-plane stresses increase significantly at the core of the salt protrusion, and the stress perturbation then begins to decrease with distance from the core (Fig. 4a, 4c). The difference is that the vertical stress has a significant increase in the protrusion core (dashed box in Fig. 4b), but the stress perturbation suddenly changes from compressive stress to extensional stress on both sides not far from the core of the protrusion (oval frame in Fig. 4b). The horizontal stress, out-of-plane stress, and vertical stress change because sediment near the protruding salt body moves horizontally from both sides to the protrusion core as well as upward in the vertical direction (Fig. 5a), resulting in horizontal and vertical compression strain (Fig 5b, 5c).
Fig. 4.
Fig. 4.
Stress perturbation and principal stress direction in the sediment around the reference salt model.
Fig. 5.
Fig. 5.
Displacement change and strain perturbations caused by viscoelastic stress relaxation of salt body in sediment.
Contrary to the stress perturbations at the salt protrusion, the horizontal stress, vertical stress and out-of-plane stress all decrease in the salt depression (Fig. 4a-4c). Both the horizontal stress and the out-of-plane stress decrease significantly at the core of the salt depression, and the stress perturbations begin to decrease with distance from the depression core (Fig. 4a, 4c). The difference is that the vertical stress has a weak tensile stress in the salt depression core, increases with distance from the core in the vertical direction, and a tensile stress area appears. However, at a distance on both sides of this tensile stress area, the stress perturbation abruptly changes from tensile stress to compressive stress (Fig. 4b). The reason for such a change of the vertical stress at the salt depression is that the sediment near the salt moves from the depression core to both sides, and moves down in the vertical direction, resulting in horizontal and vertical tensile strains (Fig. 5b, 5c).
The perturbation of shear stress is mainly concentrated in positions irregular in geometric shape (protrusions and depressions) of the salt (Fig. 4d). The compressional shear stress appears on the left side of the salt body protrusion and the tensile shear stress occurs on the right side. In contrast, the tensile shear stress occurs on the left side of the salt depression and the compressional shear stress occurs on the right side. When the sediment is far away from the irregular geometries of the salt body, the shear stress decreases significantly and approaches zero. The perturbation of the shear stress (Fig. 4d) can be explained by the change of shear deformation (Fig. 5d). For example, the material flow on the left side of the salt protrusion appears counterclockwise (Fig. 5a, left dotted frame) and the right side is clockwise (Fig. 5a, right dotted frame).
A comparison of the principal stresses and normal stress (Fig. 4) shows that the three principal stresses are very similar to the perturbation modes (extrusion or tension) of the horizontal stress, out-of-plane stress, and vertical stress, but the magnitudes are different. The horizontal stress corresponds to the maximum principal stress, the vertical stress corresponds to the minimum principal stress, and the out-of-plane stress corresponds to the intermediate principal stress. This is because the horizontal stress of the initial state of the model is determined as the maximum principal stress, the out-of-plane stress is the intermediate principal stress, and the vertical stress is the minimum principal stress when the model is set. After the stress relaxation of the salt body, the shear stress perturbation mainly occurs near the area with clear fluctuations of the salt. The principal stress directions therefore change and rotate near the protrusion and depression of the salt, while the principal stress directions basically do not change near the horizontal salt stratum (Fig. 4i).
The von Mises stress increases at the salt protrusion (dotted box on the left side of Fig. 3b), and decreases at the salt body depression (dotted box on the right side of Fig. 3b). Similarly, the mean stress increases at the salt protrusion and decreases at the depression (Fig. 4e). Previous studies have shown that the safe drilling location near the salt is usually in the area with large minimum principal stress, large mean stress and small shear stress[38,39,40]. Therefore, it is difficult to determine whether the protrusion and depression of the salt are suitable drilling locations, because both the minimum principal stress at the protrusion and the von Mises stress are large. The von Mises stress at the depression is large, but the minimum principal stress is small.
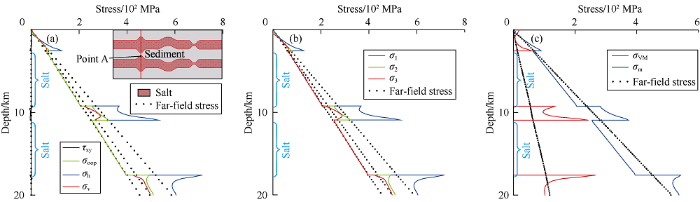
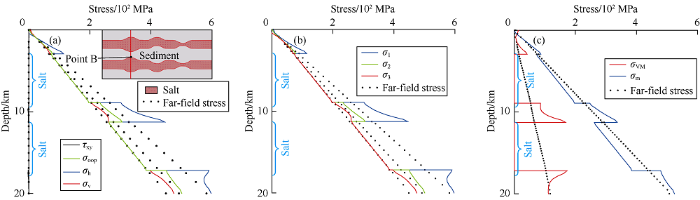
We further analyze the stress perturbations through the vertical profiles through the salt. Profile 1 passes through the salt body on the left (salt body protuberance) (Fig. 6a). Near the salt protrusion, compared to the far-field stress (initial stress), the normal stresses are all obviously increase, and the horizontal stress and out-of-plane stress increase the most near the salt body. The vertical stress starts to increase at the salt protrusion and reaches a maximum after a distance from the salt (Fig. 6a). In the salt body, both the out-of-plane stress and the horizontal stress are reduced and the magnitude is equal to the vertical stress, resulting in an isotropic stress state (Fig. 6a). The shear stress is particularly small at the profile position (Fig. 6a). The results show that the principal stress directions around the salt body after stress relaxation on the profile haves no significant change compared with the far-field principal stress directions (Fig. 6a, 6b). In Fig. 6c, both the von Mises stress and the mean stress in the salt body are reduced compared with the far-field stress, but the von Mises stress decreases more significantly, because the salt body presents an isotropic stress state, (i.e., non-deviatoric stress). The von Mises stress and mean stress in the sediment reach the maximum near the salt, and the stresses gradually decrease with distance from the salt. The von Mises stress near the bottom boundary is even smaller than that of the far-field stress.
Fig. 6.
Fig. 6.
Stress profile through salt protrusion.
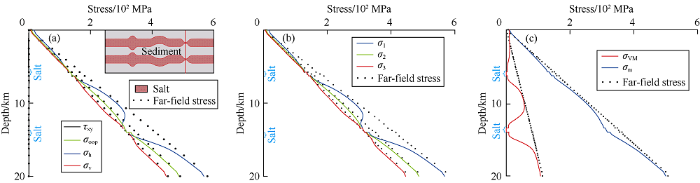
Profile 2 passes through the salt body on the right (salt body subsidence) (Fi. 7a). In the vicinity of the salt depression, the normal stresses are all reduced compared with the far-field stresses. The horizontal stress is significantly reduced in all three sediments layers, but the change of vertical stress and out-of-plane stress are not apparent, and the stress disturbance only occurs in the middle and lower sediment layers. The horizontal stress near the salt body is the smallest, and the stress value increases gradually with the distance from the salt. There is no significant change in shear stress of the entire profile compared with its far-field stress, which also explains that the principal stress directions after the salt stress relaxation are basically unchanged compared to the far-field principal stress directions (Fig. 7a, 7b). Differing from the stress perturbations at profile 1, the von Mises stress and mean stress in the sediment at profile 2 reach the minimum value near the salt body, and the stress increases gradually as it moves away from the salt body (Fig. 7c). The stresses change in the salt are similar to those in profile 1, and will not be described again. When the salt is horizontal (without geometric fluctuations), the stress perturbations to the surrounding sediment is very small or even non-existent during the process of salt stress relaxation. To further explore the relationship between the degree of fluctuation of the salt body and the stress perturbation, we also designed two comparison models by changing the salt fluctuation.
Fig. 7.
Fig. 7.
Stress profile through salt depression.
3.2. Comparison model
3.2.1. Comparison model 1
The fluctuations of the protruding salt body on the left are gentler than the reference model (dashed box in Fig. 8a) and the other model settings are the same. A comparison of the stress perturbation results in the reference model (Figs. 4 and 8) show that the stress perturbations pattern produced by the salt body stress relaxation in this model is consistent with the reference model: The horizontal stress, out-of-plane stress, vertical stress, principal stresses, mean stress, and von Mises stress all increase with the salt protuberance and decrease in the depression. The results show that the compressive shear stress appears on the left side of the protrusion and the right side of the depression, and the extensional shear stress appears on the right side of the protrusion and the left side of the depression. The difference is that the stress perturbations in the sediment are smaller than those in the reference model due to the gentle fluctuation of the salt protruding from the left side (Figs. 4a-4c and 8a-8c).
Stress perturbation in sediment around salt body in model 1.
Stress perturbation in sediment around salt body in model 1.
Fig. 8.
The profile through the salt body can more clearly shows the effect of the fluctuation of the salt body on the stress perturbation (Fig. 9). The results show that the stress change trend in the salt body is basically consistent with that in the reference model (Figs. 6 and 9). The perturbation of horizontal stress, out-of-plane stress and vertical stress are smaller than those of the reference model. Taking the horizontal stress as an example, at the interface between salt and sediment, the stress increase of the reference model ($\sigma_{h}$= 53.1 MPa, see Fig. 6a point A) is greater than that of this model ($\sigma_{h}$= 44.5 MPa, see Fig. 9a point B). The shear stress at the model profile has no significant change and is essentially 0 (Fig. 9a). Similarly, compared with the reference model, the perturbations of principal stresses, mean stress, and von Mises stress are also reduced owing to the gentler salt protuberance (Figs. 6b-6c and 9b-9c).
Fig. 9.
Fig. 9.
Stress profile through body protrusion.
3.2.2. Comparison model 2
Model 2 is characterized by a steeper fluctuation of the salt depression on the right side and the other model settings are the same as the reference model. A comparison of the stress disturbance results (Figs. 4 and 10) shows that the normal stresses decrease more significantly owing to the steeper salt depression in model 2 (Fig. 10a-10c). The perturbations of normal stresses of this model are essentially consistent with the reference model. The differences are that changes of horizontal stress in the middle sedimentary layer are relatively apparent (Fig. 11a), and the horizontal stress decreases more sharply near the salt body (Figs. 7a and 11a). The shear stress does not change with the far field and is close to zero. Compared with the reference model, the maximum principal stress perturbation is more apparent in the middle sedimentary layer because of the steeper fluctuations (Fig. 11b), and stress decreases sharply near the salt body (Fig. 11b). Similarly, the mean stress and von Mises stress in model 2 also decrease more near the salt depression than in the reference model with the reference model.
Fig. 10.
Fig. 10.
Stress perturbation in sediment around salt body in model 2.
Fig. 11.
Fig. 11.
Stress profile through salt depression.
3.3. Salt structural model of the western Kelasu
Herein we analyze the stress perturbations of several conceptual salt models of different geometric styles, as well as in an actual salt model. Model material parameters and boundary conditions are the same as the reference model.
Similar to the results of the von Mises stress in the reference model (Fig. 3), the shear stress in the salt body gradually relaxes and decreases with time due to stress relaxation in the salt body, and stress perturbations occurs in the sediment around the salt body (Fig. 12b). Stress in the final state of the model (Fig. 12c) is the sum of the initial stress (Fig. 12a) and the stress perturbations due to the viscoelastic stress relaxation of the salt.
Fig. 12.
Fig. 12.
von Mises stress perturbation.
The simulation results show that in this salt basin (similar to a large-scale salt body depression), the horizontal stress on the upper surface of the salt becomes smaller (Fig. 13a), but the vertical stress increases slightly in the central basin region (the salt body is gentle). Vertical extensional stress begins to appear on both sides of the basin (there are small-scale depressions on the left and right sides) (Fig. 13b), indicating that in large-scale salt structures, stress perturbations are affected by both the whole salt structure and the local small-scale salt structure. The lower surface of the salt body is a protrusion and a state of horizontal compression stress appears here. However, the stress gradually decreases with distance from the protrusion core. The vertical stress shows a similar situation here; the perturbation of normal stress is similar to horizontal stress, except that the value of stress perturbation is smaller (Fig. 13a, 13c). In Fig. 13d, the shear stress perturbation mainly occurs near the irregular salt geometry.
Fig. 13.
Fig. 13.
Stress perturbation in the sediments around the salt body in Kuqa depression.
The von Mises stress increases at the salt body protrusion, such as at the protrusion of the lower surface of the salt body (see the dotted box in the middle of Fig. 13i), the north Qiulitage anticline (see the dotted box on the left of Fig. 13i), and near the north Tuzimaza salt dome (see dotted box on the right of Fig. 13i); the mean stress also increases at the protuberance of the lower surface of the salt body and the north Qiulitage anticline, but decreases near the north Tuzimazar salt dome (Fig. 13e), so it is difficult to determine whether the north Qiulitage anticline is a safe drilling location because the von Mises stress and the average stress both increase. However, it is determined that the drilling location near the north Tuzimaza salt dome is not suitable because the von Mises stress increases and the average stress decreases.
4. Discussion
In this study we designed and simulated three sets of double-layered salt body models with three depressions and protrusions. It is found that the salt geometry is strongly related to the stress perturbations in the sediments around the salt body, which is consistent with many previous studies[15-16,41]. The model results show that under a background extrusion stress field, the stress perturbations produced by the protruding salt body and the depression salt body are opposite (extrusion and tension). Moreover, the fluctuation degree (steep or gentle) of the protrusions and depressions will affect the stress perturbation. The model results are applied to the actual salt structure model (Kuqa depression, Tarim Basin).
The perturbations of minimum principal stress, mean stress, and von Mises stress are comprehensively considered in drilling stability analysis[15,42-45]. According to the Mohr Coulomb or Drucker Prager criterion, an increase of mean stress indicates that the material can bear more shear stress and is less prone to deformation or fracture, whereas increased von Mises stress means that the material is closer to yield. The ideal drilling trajectory should therefore be designed where the average stress is large and the von Mises stress is small. The results of this study show that the gentle fluctuation of a salt depression is an ideal drilling location because, compared with the far-field stress, the von Mises stress decreases substantially and the mean stress decreases slightly (Figs. 3b and 4e).
The two-dimensional plane strain model in this study also has some limitations. For example, the geometry and movement of the salt body in the third dimension is not considered and local temperature anomalies can produce temperature stresses[46]. The fault zone around the salt body will also lead to perturbations of stress and pore pressure. Under certain geological conditions, a change of pore fluid pressure can cause effective stress perturbation and affect drilling design. If this factor is considered, the proposed drilling position may change. This study does not include simulation of the pore fluid pressure[15]. Therefore, when analyzing the actual drilling design, attention must be paid to the applicability of the simu-lation results presented here. Combined with further geological and geophysical research and more information regarding the above factors, a more realistic model can be built to further simulate and study the influence of these factors on the stress perturbations around the salt body to obtain a more realistic stress field and pore fluid pressure field and better guide for drilling design.
5. Conclusions
Three double-layer salt body models of combined protuberance and depression and one salt structure model of the Kuqa depression in Tarim Basin were designed using geomechanical modeling methods, and the stress perturbations around the salt body were simulated. Stress perturbations caused by the stress relaxation of the salt body under compressional tectonic stress conditions were studied and the following conclusions were obtained.
The stress perturbations of a salt body have an important relationship with salt body geometry. Under a background extrusion stress field, compressional stress perturbations occur near the protrusion, extensional stress perturbations near the salt body of depression, and no stress perturbation around the horizontal salt body (without geometrical abnormality).
The fluctuation degree of salt protrusions and depressions also affect stress perturbations. The steeper the fluctuation of the protrusion or depression, the greater the stress perturbations; conversely, the gentler the fluctuation of the protrusion or depression, the smaller the stress perturbations.
In the salt structure of the Kuqa depression, the stress perturbations are affected by both the geometry of the whole salt structure and the geometry of the local small-scale salt structure. If the pore fluid pressure is not taken into account, the best drilling location is where the average stress is large and the von Mises stress is small, which is the salt depression in this study. If the pore fluid pressure is considered, the optimal drilling position may change.
Nomenclature
D—matrix of elastic materials;
$\{d \varepsilon \}$—strain increment, dimensionless;
$\{d \varepsilon ^{e}\}$—viscous strain increment, dimensionless;
$\{d \varepsilon ^{v}\}$—elastic strain increment, dimensionless;
E—elastic modulus, GPa;
Q—viscosity matrix, Pa•s;
t —time, s;
$\sigma^{t}$—stress increment, MPa;
$\sigma_{h}$—horizontal stress, MPa;
$\sigma_{v}$—vertical stress, MPa;
$\sigma_{VM}$—von Mises stress, MPa;
$\sigma_{oop}$—normal stress, MPa;
$\sigma_{1}$—maximum principal stress, MPa;
$\sigma_{2}$—intermediate principal stress, MPa;
$\sigma_{3}$—minimum principal stress, MPa;
h—viscosity, Pa•s;
v—Poisson's ratio, dimensionless;
$\sigma_{ij}$—stress tensor, Pa;
gi—gravitational acceleration, m/s2;
ρ—density, kg/m3.
Reference
Retrospective salt tectonics: JACKSON M P A, ROBERTS D G, SNELSON S. Salt tectonic: A global perspective
Salt tectonism in the Persian Gulf Basin
DOI:10.1144/GSL.SP.1996.100.01.10 URL [Cited within: 1]
The effect of allochthonous salt on the petroleum systems of northern Green Canyon and Ewing Bank(Offshore Louisiana), northern Gulf of Mexico
Oil and gas resources in salt-bearing basins in the world
The particularity of subsalt and drilling fluid techniques
An overview on salt structures
The drilling technology for penetrating carbonate formation in Tarim Deep Wells
Dynamic evolution assessment of the Paleozoic hydrocarbon cap rocks in Bachu-Magati area, Tarim Basin
Numerical modeling and optimum engineering design for hole shrinkage in borehole drilling at salt and gypsum layers
Numerical studies of the deformation of salt bodies with embedded carbonate stringers
Comparison of evolutionary and static modeling of stresses around a salt diaper
DOI:10.1016/j.marpetgeo.2014.07.002
URL
[Cited within: 1]

We compare an evolutionary with a static approach for modeling stress and deformation around a salt diapir; we show that the two approaches predict different stress histories and very different strains within adjacent wall rocks. Near the base of a rising salt diapir, significantly higher shear stresses develop when the evolutionary analysis is used. In addition, the static approach is not able to capture the decrease in the hoop stress caused by the circumferential diapir expansion, nor the increase in the horizontal stress caused by the rise of the diapir. Hence, only the evolutionary approach is able to predict a sudden decrease in the fracture gradient and identify areas of borehole instability near salt. Furthermore, the evolutionary model predicts strains an order of magnitude higher than the strains within the static model. More importantly, the evolutionary model shows significant shearing in the horizontal plane as a result of radial shortening accompanied by an almost-equivalent hoop extension. The evolutionary analysis is performed with ELFEN, and the static analysis with ABAQUS. We model the sediments using a poro-elastoplastic model. Overall, our results highlight the ability of forward evolutionary modeling to capture the stress history of mudrocks close to salt diapirs, which is essential for estimating the present strength and anisotropic characteristics of these sediments. (C) 2014 Elsevier Ltd.
Stress perturbations adjacent to salt bodies in the deep-water Gulf of Mexico
Geomechanical modeling of salt diapirs: Generic shapes and a 3-D salt structure from the Officer Basin, South Australia
Geomechanical effects of a 3-D vertical salt well drilling by FEA
Geomechanical modeling of stresses adjacent to salt bodies: Part 1-Uncoupled models
DOI:10.1306/04111110144
URL
[Cited within: 5]

We compare four approaches to geomechanical modeling of stresses adjacent to salt bodies. These approaches are distinguished by their use of elastic or elastoplastic constitutive laws for sediments surrounding the salt, as well as their treatment of fluid pressures in modeling. We simulate total stress in an elastic medium and then subtract an assumed pore pressure after calculations are complete; simulate effective stress in an elastic medium and use assumed pore pressure during calculations; simulate total stress in an elastoplastic medium, either ignoring pore pressure or approximating its effects by decreasing the internal friction angle; and simulate effective stress in an elastoplastic medium and use assumed pore pressure during calculations. To evaluate these approaches, we compare stresses generated by viscoelastic stress relaxation of a salt sphere. In all cases, relaxation causes the salt sphere to shorten vertically and expand laterally, producing extensional strains above and below the sphere and shortening against the sphere flanks. Deviatoric stresses are highest when sediments are assumed to be elastic, whereas plastic yielding in elastoplastic models places an upper limit on deviatoric stresses that the rocks can support, so stress perturbations are smaller. These comparisons provide insights into stresses around salt bodies and give geoscientists a basis for evaluating and comparing stress predictions.
Geomechanical modeling of the Mad Dog salt, Gulf of Mexico
Reservoir fracture distribution law of kuche depression in Talimu Basin
Kinematics characteristics of the Kuqa Depression in the Tarim Basin
This paper quantitatively describes the net growth, net growth rate and strain rate of the salt structures in the Kuqa depression and illustrates the salt movement characteristics of Kuqa depression based on analysis of abundant seismic and geological data. The first movement of the salt began in the early Miocene, when the salt structure grew slowly and stably. The fast growth of the salt structure took place from the middle-late Pliocene to Quaternary, featuring quick and differentiated growth. The salt structure in the Kuqa depression has five continuous growth stages: sedimentation of salt and gypsum, slow growth of low-relief salt pillows, development of salt anticlines, salt diapir expansion and breakage of salt diapir piercement.
Tertiary salt pillow structures in the central sector of the Kuqa foreland fold-and-thrust belt, Tarim Basin, northwest China
Salt structure characteristics and its relation to hydrocarbon accumulation in the Kuqa Depression, Tarim Basin
The salt-related structures and their formation mechanisms in the Qiulitag structural belt, Kuqa Depression
Cenozoic salt tectonics and physical models in the Kuqa depression of Tarim Basin, China
Salt-related structural style of Kuqa foreland fold belt
Internal deformation features of detachment layers in the front of the Kuqa forland fold-thrust belt
Thrust and fold tectonics and the role of evaporites in deformation in the Western Kuqa Foreland of Tarim Basin, Northwest China
Oil exploration breakthrough in the Wensu salient, northwest Tarim Basin and its implications
Distribution of earth stress in Kuche thrust belt, Tarim Basin
An analysis of the Mesozoic2Cenozoic Tectonic Stress Field in Kuqa Depression, Tarim Basin
Balingshan-Huayuan multilayer salt and salt mud tectonics in Jiangling Depression and its formation mechanism
New discovery of oil and gas in the flank of Balingshan-Huayuan anticline structure in the recent years makes it necessary to have a further understanding of its structural nature. Based on the interpretation of seismic profiles, it is considered that K2y-Ex is the superimposition of salt and mud tectonics, and can be divided into salt domesalt pillar multilayered superimposed structure, salt mud domesalt mud pillar structure and salt mud dome structure. The formation of salt mud tectonics was the superposition effect of plasticized salt mud stone bedding creep which led to thickening of the single layer and the multilayer cumulation. Reverse fault was formed by the salt mud intrusion along the early hanging wall of fault and the diapirism, thus the fault had the characteristics of the upper bed showing reverse and the lower showing normal. Differential loading and volcanic thermal convection were the dominant dynamic mechanisms. The salt dome-salt pillar of K2yLower Es occurred at the Middle Eocene with the main formation stage of the Late Oligocene, the salt mud tectonics of upper Es-Ex occurred at the Late Oligocene, and both of them finalized basically in Pleistocene. The salt mud tectonic wing strata-salt mud sealing barrier trap and the lithologic updip pinch outsalt mud sealing barrier trap are the potential oil and gas reservoir exploration types.
Characteristics of salt structures and links to Pb-Zn mineralization of the Jinding Deposit in Lanping Basin, Western Yunnan
Passive-margin salt basins: Hyperextension, evaporite deposition, and salt tectonics
DOI:10.1111/bre.12043
URL
[Cited within: 1]

Passive-margin salt basins are classified as prerift, syn-stretching, syn-thinning, and syn-exhumation. Prerift salt, such as the Triassic Keuper in the Western Pyrenees, undergoes thick-skinned extension, first decoupled and then coupled, along with its substrate and cover. The base salt develops significant relief, is attenuated on the largest faults, and ends up distributed across the entire margin. Syn-stretching salt, such as along the Iberian and Newfoundland margins, is deposited during early rifting and is thus concentrated in proximal areas with variable thickness and extent, with decoupled and coupled thick-skinned deformation dominant. Syn-thinning salt, such as in the northern Red Sea, is also deposited during extension, with the base salt unconformably above proximal stretching faults but offset by distal thinning faults. Both thick-skinned and gravity-driven thin-skinned deformation occur, with the latter strongly influenced by the ramp-flat geometry of the base salt. Syn-exhumation salt, such as in the Gulf of Mexico and South Atlantic salt basins, is deposited as part of the sag basin with broad distribution and a generally unfaulted base. Conjugate syn-exhumation salt basins are originally contiguous, form partly over exhumed mantle on magma-poor margin segments, and are commonly flanked by magma-rich segments with volcanic highs (seaward-dipping reflectors) that isolate the salt basin from marine water. Salt tectonics is characterized by gravitational failure of the salt and overburden, with proximal extension and distal contraction, and the development of allochthonous salt that includes frontal nappes that advance over newly formed oceanic crust.
ABAQUS Abaqus user guide and help documentation
The role of pore fluid overpressure in the substrates of advancing salt sheets, ice glaciers, and critical-state wedges
DOI:10.1002/2014JB011326 URL [Cited within: 5]
Application of the critical taper model in the subsalt structural wedges: Example from Kelasu structure belt of Kuqa Depression
Structural fracture distribution and prediction of the Lower Jurassic Ahe Formation sandstone in the Yinan-Tuzi Area, Kuqa Depression
DOI:10.1002/(sici)1097-0134(19991201)37:4<592::aid-prot10>3.0.co;2-2
URL
PMID:10651275
[Cited within: 2]

A new method for the homology-based modeling of protein three-dimensional structures is proposed and evaluated. The alignment of a query sequence to a structural template produced by threading algorithms usually produces low-resolution molecular models. The proposed method attempts to improve these models. In the first stage, a high-coordination lattice approximation of the query protein fold is built by suitable tracking of the incomplete alignment of the structural template and connection of the alignment gaps. These initial lattice folds are very similar to the structures resulting from standard molecular modeling protocols. Then, a Monte Carlo simulated annealing procedure is used to refine the initial structure. The process is controlled by the model's internal force field and a set of loosely defined restraints that keep the lattice chain in the vicinity of the template conformation. The internal force field consists of several knowledge-based statistical potentials that are enhanced by a proper analysis of multiple sequence alignments. The template restraints are implemented such that the model chain can slide along the template structure or even ignore a substantial fraction of the initial alignment. The resulting lattice models are, in most cases, closer (sometimes much closer) to the target structure than the initial threading-based models. All atom models could easily be built from the lattice chains. The method is illustrated on 12 examples of target/template pairs whose initial threading alignments are of varying quality. Possible applications of the proposed method for use in protein function annotation are briefly discussed.
Rock mechanical properties and brittleness evaluation of shale reservoir
Rock mechanical properties of shale gas reservoir are vitally important for exploitation. It is necessary to conduct laboratory study on mechanical properties and brittleness evaluation of shale, which can provide technical support for drilling and fracturing design. Experimental investigations show that compressive strength has positive correlations with Young's modulus and confining pressure. Volume change of rocks before and after fracturing increases with decreased Young's modulus and increased Poisson's ratio. Failure mode under low confining pressure is predominantly splitting failure, while shear failure mode is dominant under high confining pressure. Brittleness of shale has close relations with shale elastic parameters and mineral constituent. Based on numerical modeling and experimental measurement, in combination with elastic parameters method and mineral constituent method, a new brittleness evaluation method is proposed, and brittleness evaluation of single wells is realized which has better effect. Brittleness evaluation is useful for understanding reservoir mechanics and selecting fracture section.
Spatial-temporal migration of earthquakes in the northeastern Tibetan Plateau: Insights from a finite element model
Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion
Stability analysis of deviated boreholes using the Mogi-Coulomb failure criterion, with applications to some oil and gas reservoirs
Near-salt stress and wellbore stability: A finite-element study and its application
Coupling geomechanical modeling with seismic pressure prediction
Lessons learned in the planning and drilling of deep, subsalt wells in the deepwater Gulf of Mexico
Challenges of drilling an ultra-deep well in deepwater-spa prospect
Geomechanics considerations for through and near-salt well design
Influence of temperature perturbation on borehole wall stabilization and oil field development