Introduction
Gas condensate initially exists in gas phase in a reservoir when the reservoir pressure is above the dew-point pressure (DPP). When the reservoir pressure drops below the DPP, liquid oil starts to drop out, forming a condensate ring around the wellbore which would block the flow of natural gas and thus lead to the reduction of gas effective permeability. When the reservoir pressure drops below the DPP, the gas productivity will decrease rapidly[1]. Moreover, a substantial amount of condensate remains in the reservoir, and is difficult to recover. Calculating the DPP accurately is particularly important for the development of gas-condensate reservoirs.
DPP can be measured most accurately by constant composition expansion experiments. But the experiment takes money and time; the effect of the experiment also depends on whether there is a large enough sample, and human error is hard to eliminate when recombining separator oil and gas samples. Therefore, it is necessary to find a simple and accurate method for DPP calculation.
Some mathematical methods have been previously proposed for predicting DPP when reliable samples are unavailable, or when performing pressure-volume-temperature (PVT) experiments is difficult[1-2] . In general, they include two kinds: equations of state (EOS) and empirical correlations. Many studies on using different EOS to characterize fluid behavior in condensate gas reservoirs have been conducted[3,4,5,6,7]. Of these methods, the EOS proposed by Soave[3], and Peng and Robinson[5] are regarded as the most reliable for calculating the properties of reservoir fluids[8-9] . However, the predictions of EOS are not unique because the EOS schemes splitting fractions, and characterization methods of fractions, and binary interaction coefficients that used in the prediction may be different[1]. Empirical correlations are an alternative approach for DPP calculation. However, the application of an empirical correlation is limited to the range of data used in its development. Of the two types of empirical correlations, one depends on the composition and properties of the heptane-plus fraction, and the other depends on production data. In the well-known first type of correlation, DPP is expressed as a function of composition and reservoir temperature[1,10-15]. In the second type of empirical correlations, DPP is expressed as a function of production data and reservoir temperature[16,17,18,19,20] .
In this study, the accuracy and applicable scope of previously published methods for DPP calculation have been evaluated, a new correlation for the estimation of DPP of gas-condensate reservoirs has been established and compared with the correlations and EOS published before.
1. Methods
1.1. Workflow
A large amount of data was collected from various sources, and a large data bank was built. On this basis, the EOSs and correlations published before were evaluated, and a new mathematical correlation was developed to improve DPP estimation in the absence of reliable samples or when experimental work cannot be performed.
1.2. Measurement of dew-point pressure
The DPPs of six gas condensate samples were measured using the automated mercury-free PVT cell fluid evaluation analyzer (VINCI) at the Petroleum Fluid Research Center, Kuwait University. Of them, some were taken from well bottom, and the others from surface separators. The DPP, initial composition, and gas/oil ratio of the samples taken from well bottom were measured by the constant composition expansion test (also known as constant mass depletion (CMD)) and the flash vaporization method. The oil and gas samples taken from separators were recombined based on the initial gas/oil ratio, and the composition was checked against the samples taken from well bottom. The CMD test was performed using the Macro Software, in which each sample was put at the reservoir temperature first; secondly, the pressure was adjusted to the initial reservoir pressure; thirdly, the pressure was reduced further until retrograde condensed liquid came up, and then the DPP was measured. A gas chromatograph (Agilent 7890B) was used to test the compositions of the separator gas and oil samples that were to be recombined based on the field gas/oil ratio, and the reservoir fluid composition was calculated. Table 1 shows the tested composition, relative molecular weight, and relative density of C7+ wellbore fluid, and the DPP of the wellbore fluid.
Table 1 Experimental data of the six gas condensate samples.
| Sample No. | Molar fraction of each component/% | Reservoir temperature/°C | C7+ relative molecular weight | C7+ relative density | DPP/ MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | |||||
| a | 73.40 | 9.40 | 3.72 | 1.92 | 0.85 | 0.84 | 1.62 | 0.80 | 7.44 | 0 | 137 | 147.55 | 0.765 87 | 31.7 |
| b | 69.05 | 6.36 | 6.22 | 4.41 | 1.90 | 2.47 | 8.32 | 0.27 | 1.00 | 0 | 113 | 142.84 | 0.757 90 | 37.3 |
| c | 87.10 | 6.52 | 2.02 | 1.09 | 0.48 | 0.46 | 1.23 | 0.51 | 0.59 | 0 | 99 | 128.90 | 0.768 58 | 23.8 |
| d | 70.89 | 7.71 | 4.32 | 3.35 | 2.96 | 4.81 | 4.92 | 0.59 | 0.45 | 0 | 80 | 118.61 | 0.762 28 | 18.3 |
| e | 71.45 | 10.85 | 5.07 | 2.59 | 1.35 | 1.37 | 3.29 | 0.17 | 3.67 | 0 | 154 | 135.58 | 0.768 10 | 42.9 |
| f | 78.00 | 8.69 | 5.42 | 2.88 | 1.13 | 0.93 | 1.47 | 1.12 | 0.36 | 0 | 81 | 126.76 | 0.763 10 | 13.9 |
2. Data gathering and screening
In this study, most of the data were collected from existing literatures. A total of 925 samples were gathered from previous research (579 samples from Nemeth and Kennedy[13] and 340 unpublished samples from Elsharkawy[1]). In addition, six samples were measured by us at the Kuwait University Research Center. The collected data were screened to remove repeated and defective samples. During the screening process, the sum of the mole fractions (which should be 1.0), relative molecular weight, C7+ mole fraction, and C1 mole fraction were checked.
2.1. Identification of gas condensate
It can be seen from Table 2 that the identification criteria proposed by different researchers have significant differences in GOR and relative density. According to the identification method proposed by Lake and Holstein[23] based on composition and molecular weight (Table 3), the identification criteria in Table 2 could wrongly take other reservoir fluids as gas condensate. It is important to note that most of the published literatures have no GOR and relative density data.
Table 2 Identification criterion of gas condensate based on gas-oil ratio (GOR), relative density, and mole fraction of C7+.
Table 3 Identification criteria of reservoir fluids based on molecular weight and C7+ mole fraction (Lake and Holstein[23]).
| Identification criterion | Initial fluid molecular weight | C7+ mole fraction/% |
|---|---|---|
| Heavy oil and tar | >210 | >50 |
| Black oil | 70-210 | 35-50 |
| Volatile oil | 40-70 | 10-30 |
| Gas condensate | 23-40 | 1-6 |
| Wet gas and dry gas | <23 | 0-1 |
2.2. Removal of repeated and faulty samples
First, the repeated samples were removed. Then, the samples for which the sum of the mole fractions was not equal to one ($\sum$Zi$\ne$1) were eliminated. These abnormal samples could be the result of reporting errors during the measurement of composition or typing errors in the published studies.
2.3. Relative molecular weight (MWt=$\sum$ZiMWi)
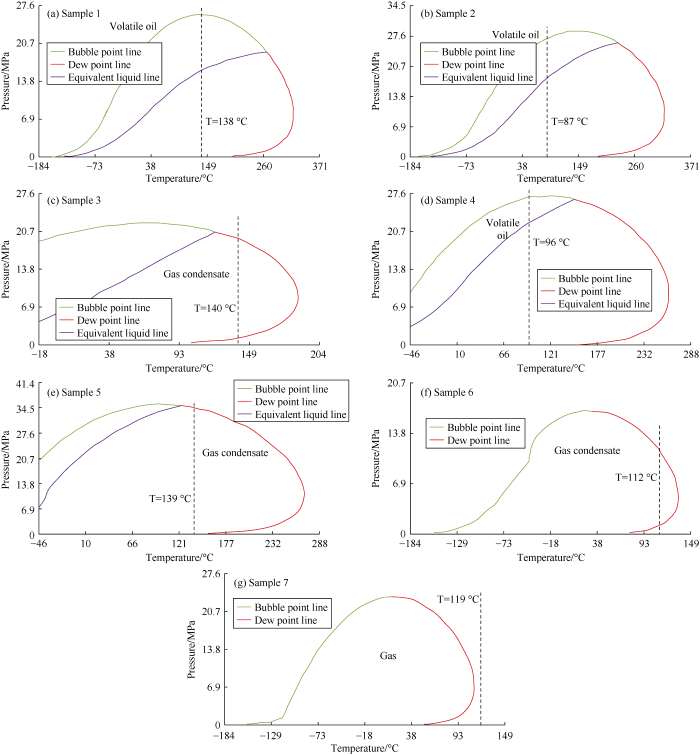
According to Table 3, typical gas-condensate has a relative molecular weight from 23 to 40. The phase envelopes of all the samples were plotted with PVTi software. It is found that the samples with relative molecular weight of more than 40 show features of volatile oil, so they were eliminated. Then the envelops of samples with relative molecular weight of less than 40 were checked one by one. It was found that some samples with molecular weight ranging from 35 to 40 had features of gas condensate, while others had features of volatile oil. Therefore, for the samples with relative molecular weight of 23-40, the samples with phase envelop showing volatile oil features were screened out too. The samples with a molecular weight of less than 23 were checked with the same method. The screening process of samples according to relative molecular weight and phase envelop are shown in Table 4 and Fig. 1.
Table 4 Samples used in the screening process according to relative molecular weight criterion.
| Sample No. | Reservoir temperature/°C | Mole fraction of each component/% | Relative molecular weight | Fluid type | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | ||||
| 1 | 138 | 55.8 | 9.3 | 5.9 | 3.7 | 2.6 | 2.2 | 17.2 | 0.5 | 2.8 | 0 | 54 | Volatile oil |
| 2[13] | 87 | 58.5 | 13.4 | 7.3 | 4.0 | 2.0 | 1.6 | 11.9 | 0.4 | 0.9 | 0 | 42 | Volatile oil |
| 3[13] | 140 | 39.7 | 9.4 | 6.6 | 6.3 | 4.2 | 3.4 | 8.9 | 10.9 | 5.1 | 5.5 | 39 | Gas condensate |
| 4[13] | 96 | 60.0 | 14.5 | 7.6 | 4.0 | 2.2 | 1.4 | 9.4 | 0.6 | 0.3 | 0 | 37 | Volatile oil |
| 5 | 139 | 68.6 | 7.3 | 4.0 | 2.4 | 1.5 | 1.3 | 8.6 | 0.9 | 5.4 | 0 | 35 | Gas condensate |
| 6[13] | 112 | 96.7 | 1.2 | 0.3 | 0.2 | 0.3 | 0.1 | 0.6 | 0 | 0.6 | 0 | 18 | Gas condensate |
| 7[13] | 119 | 95.4 | 0.8 | 0.5 | 0.4 | 0.2 | 0.1 | 1.0 | 0.3 | 1.3 | 0 | 18 | Wet gas |
Fig. 1.
Fig. 1.
Phase envelops of selected samples based on relative molecular weight (MWt).
2.4. Mole fraction of Heptane-Plus (C7+)
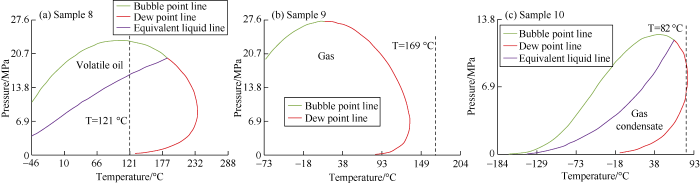
After filtering based on the relative molecular weight, the samples were screened based on the mole fraction of C7+. According to Table 3, gas condensate has mole fraction of C7+ from 1% to 6%, whereas volatile oil has mole fraction from 10% to 30%. However, Table 2 shows that the gas condensate samples have C7+ mole fractions below 12.5% in general, and as high as 15% in exceptional cases. Samples with a mole fraction of C7+ greater than 11% were rejected because their phase envelopes show volatile oil features. Among the samples with a mole fraction of C7+ ranging from 6% to 11%, some show behavior of gas condensate, and some show behavior of volatile oil. When the mole fraction of C7+ is more than 1%; most of the samples show the behavior of gas condensate. Only a few samples show the behavior of wet gas. For example, sample 9 has C7+ mole fraction of 0.4% and falls within the wet-gas region at the given reservoir temperature. In contrast, even with zero C7+ mole fraction, sample 10 has phase envelope of gas condensate features. Examples of the screening process are shown in Table 5 and Fig. 2.
Table 5 Examples of samples screened based on the C7+ mole fraction criterion.
| Sample No. | Reservoir temperature/°C | Mole fraction of each component/% | Relative molecular weight | Fluid type | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | ||||
| 8 | 121 | 63.4 | 4.6 | 3.2 | 3.8 | 3.7 | 4.5 | 14.5 | 1.5 | 0.8 | 0 | 43 | Volatile oil |
| 9 | 169 | 79.1 | 1.5 | 0.4 | 0.2 | 0.1 | 0.1 | 0.4 | 11.6 | 6.5 | 0.1 | 20 | Wet gas |
| 10[13] | 82 | 58.3 | 2.7 | 1.0 | 37.4 | 0 | 0 | 0 | 0.3 | 0.3 | 0 | 32 | Gas condensate |
Fig. 2.
Fig. 2.
Phase envelop of samples screened based on mole fraction of C7+.
2.5. Mole fraction of methane (C1)
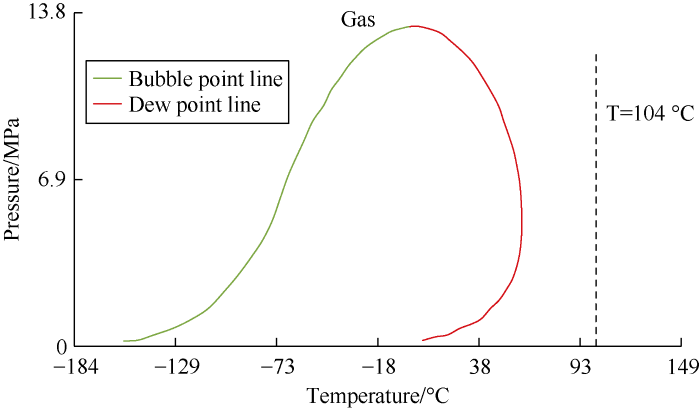
Finally, the samples were screened according to the mole fraction of C1. Gas samples generally have high C1 content; therefore, the phase envelopes of samples with a C1 mole fraction of greater than 90% were examined by using PVTi. For example, sample 11 has mole fractions of C1 and C7+ of 94.5% and 1.6%, respectively (Table 6). The reservoir temperature of the sample is 104 °C, higher the critical condensation temperature (49 °C). Phase envelope of the sample exhibits wet-gas features (Fig. 3). Phase envelop of Sample 7 also shows characteristics of wet gas. Samples with a low mole fraction of C1 can also exhibit gas condensate behavior. For example, sample 10, even though with C1 content of 58% and C7+ content of 0%, still show features of gas condensate in phase envelop (Fig. 2c).
Table 6 Examples of samples by the C1 mole fraction criterion.
| Sample No. | Reservoir temperature/°C | Mole fraction of each component/% | Relative molecular weight | Fluid type | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | ||||
| 7[13] | 119 | 95.4 | 0.3 | 0.5 | 0.4 | 0.2 | 0.1 | 1.1 | 0.3 | 1.3 | 0 | 18 | Wet gas |
| 11 | 104 | 94.5 | 1.7 | 0.9 | 0.6 | 0.3 | 0.3 | 1.6 | 0 | 0.1 | 0 | 20 | Wet gas |
Fig. 3.
Fig. 3.
Phase envelope of Sample 11.
After screening with the above methods, the number of samples was reduced from 925 to 715. Statistical analysis was done on the 715 samples (Table 7). The results of sample screening show that the margins stated in Tables 2 and 3 are not necessarily accurate. Therefore, we recommend that the classification of reservoir fluids should not be based on production data such as GOR and relative density, nor on the mole fraction of heptane-plus, but should be based on the phase envelope of reservoir fluid.
Table 7 Statistical description of the dataset used in this study.
| Index | Reservoir temperature/°C | Mole fraction of each component/% | C7+ relative molecular weight | C7+ relative density | DPP/ MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | |||||
| Max | 164 | 96.6 | 14.8 | 12.3 | 37.5 | 13.5 | 6.1 | 10.8 | 43.2 | 16.2 | 29.9 | 253.0 | 0.93 | 81.6 |
| Min | 4 | 33.3 | 0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10.8 |
| Average | 96 | 80.2 | 5.8 | 2.9 | 2.3 | 1.2 | 0.9 | 3.6 | 1.1 | 1.3 | 0.6 | 142.7 | 0.70 | 32.4 |
3. Evaluation of published correlations and equations of state
The empirical correlations with compositional data as inputs and the uncorrected PR equation of state were evaluated in this study. This type of correlations commonly used include those proposed by Nemeth and Kennedy[1], Elsharkawy[11], Shokir[13], and Godwin[26]. Because all these correlations take heptane-plus components as one group, it is logical to compare the performance of these correlations with the uncorrected EOS.
3.1. Statistical evaluation of the accuracy of published correlations and EOS
The average absolute error (AAE), average relative error (ARE), root mean square error (RMSE), and R-squared (R2) parameters were used to statistically evaluate the above-mentioned correlations and the uncorrected Peng-Robinson EOS[5], and the results are shown in Table 8. It can be seen from Table 8 that among all the correlations considered, the Nemeth and Kennedy correlation[13] has the highest accuracy. This finding is not surprising because most of the data used in this study were used in the development of the Nemeth and Kennedy correlation. In general, the Nemeth-Kennedy correlation is applicable across the entire range of input parameters. However, it can underestimate the DPP of some samples with low mole fractions of intermediate components (C2, C3, C4, and C5). The low fractions of intermediate components are counterbalanced by high mole fractions of C1 or nonhydrocarbons. Statistically, the Elsharkawy correlation[1] shows the second-best accuracy and can give good predictions for most of the data range except for the samples with very high and very low C1 mole fractions, and high nitrogen and hydrogen sulfide mole fractions. The Godwin correlation[11] is the third-best in terms of accuracy. It underestimates the DPP of samples with a very low mole fraction of C1 and no C7+. In addition, it yields DPP with large errors for samples with high mole fractions of non-hydrocarbons and/or intermediate components (accompanied with relatively low C1 content). The Shokir correlation[26] is the least accurate. A negative R2 value means that its prediction results are not reliable and invalid. Our explanation for the high errors of the Shokir correlation is that it cannot predict the DPP of samples with no C7+ components. For such samples, the DPPs calculated by Shokir correlation are negative, which is physically impossible. In addition to these four correlations, the uncorrected Peng-Robinson EOS was also used to estimate the DPPs for the dataset with the PVTi software. In the solution of PR EOS, the splitting scheme used was lumped C7+; the relation between critical pressure and critical temperature, and the relation of deviation factor used were all Kesler-Lee correlation. Table 8 shows that Nemeth-Kennedy and Elsharkawy correlations have higher accuracy than Peng-Robinson EOS in estimating the DPPs of the samples considered in this study. Among the six statistical errors reported in Table 8, the average absolute error (AAE) is the most conclusive index to judge the accuracy of each method.
Table 8 Statistical evaluation results of published correlations and PR- EOS.
| Correlation | AAE/ % | Max AAE/% | Min AAE/% | ARE/ % | RMSE | R2 |
|---|---|---|---|---|---|---|
| Nemeth and Kennedy | 8.79 | 55 | 0.03 | -4.88 | 666 | 0.83 |
| Elsharkawy | 12.53 | 115 | 0.00 | 6.07 | 791 | 0.77 |
| Shokir | 27.84 | 1421 | 0.02 | -3.12 | 2270 | -0.92 |
| Godwin | 19.61 | 96 | 0.05 | 19.61 | 1100 | 0.55 |
| PR EOS | 20.76 | 80 | 0.13 | 19.81 | 1416 | 0.26 |
3.2. Analysis of equation of state
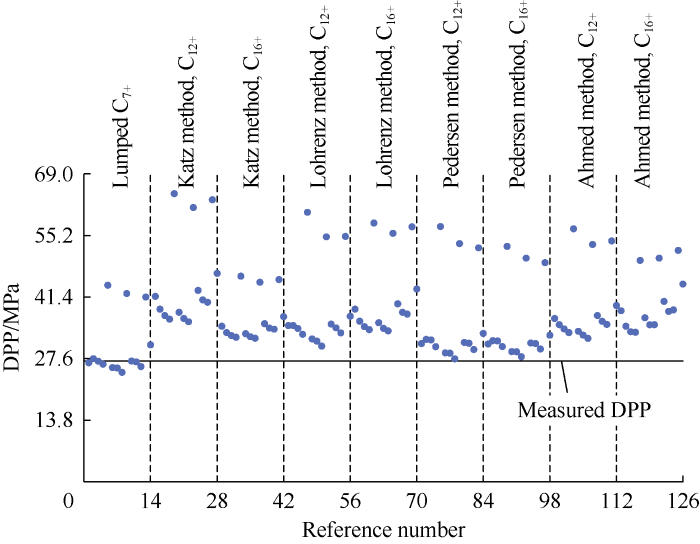
It has been stated previously that the DPP from EOS is not unique and depends on the number and division of pseudo- fractions. In this section, we show how the number and division of subfractions affect the DPP value calculated from EOS. The changing parameters considered in the analysis were the C7+ characterization correlation and splitting scheme (Table 9), while the binary interaction coefficients were kept constant. In each scheme, two cases of splitting C12+ and C16+ from C7+ fraction were considered (evaluated as two cases), and the PVTi software was used to run the three-parameter Peng-Robinson EOS with its built-in set of plus fraction characterization correlation considered. In sample 12, the mole fractions of C1, C2, C3, C4, C5, C6, C7+, N2, CO2 and H2S are 81.3%, 4.8%, 2.3%, 1.7%, 1.3%, 1.4%, 4.3%, 1.9%, 1.1% and 0 respectively. This sample has a C7+ relative density of 0.74, C7+ relative molecular weight of 139.9, reservoir temperature of 54 °C, and DPP of 27.0 MPa.
Table 9 Splitting schemes and characterization methods considered in this study.
A total of 126 possible combinations were obtained by changing these parameters, and thus 126 values of DPP were calculated (Fig. 4).
Fig. 4.
Fig. 4.
Results of EOS calculation.
Fig. 4 shows the EOS has no unique solution. In this example, it has 126 results. The complexity further increases if the binary interaction coefficient changes. Moreover, fine-tuning a customized EOS for a certain sample is complex, time-consuming, and not necessarily accurate.
4. Development of a new correlation
First, the published correlations were improved by refitting their coefficients. Next, a new correlation for DPP estimation was built.
4.1. Improving the accuracy of published correlations
The Nemeth and Kennedy, Elsharkawy, Shokir, and Godwin correlations have several constant coefficients. These coefficients were numerically derived based on the data used for developing each correlation. Our data bank was utilized to modify the four correlations by updating their coefficients and minimizing error.
Table 10 shows the accuracy of the correlations before and after modification. The Nemeth and Kennedy correlation shows the minimum improvement after modifying the coefficients. This is because most of the samples collected for this study are those used when Nemeth and Kennedy correlation is developed[13]. The modified Elsharkawy correlation has a small improvement after modification, because the rest of the data used in this study are the unpublished data provided by Elsharkawy, whereas Shokir and Godwin correlations have noticeable improvements in accuracy after modification.
Table 10 Statistical parameters of the original and modified correlations.
| Correlation | AAE/% | Max AAE/% | RMSE | R2 | |
|---|---|---|---|---|---|
| Nemeth and Kennedy | Original | 8.79 | 55 | 666 | 0.83 |
| Modified | 7.95 | 54 | 611 | 0.86 | |
| Elsharkawy | Original | 12.53 | 115 | 791 | 0.77 |
| Modified | 9.62 | 83 | 677 | 0.83 | |
| Shokir | Original | 27.84 | 1421 | 2271 | -0.92 |
| Modified | 14.41 | 242 | 890 | 0.71 | |
| Godwin | Original | 19.61 | 96 | 1100 | 0.55 |
| Modified | 10.75 | 85 | 763 | 0.78 | |
4.2. Development of new correlation
First, the input and output parameters were analyzed to find out the relationships between them and the possibility of grouping these parameters. Table 11 shows the correlation coefficients between DPP and other parameters. It can be seen from the table that the DPP decreases as the mole fraction of intermediate components increases, but is in positive correlation with mole fraction, relative molecular weight, and relative density of C7+. Compared with other variables, the non-hydrocarbon has less effect on DPP. These observations are in good agreement with the findings of Elsharkawy[1] and Shokir et al.[26]. The correlation between DPP and mole fraction of C1 in Table 11 is also consistent with the Shokir correlation.
Table 11 Correlation coefficients between DPP and the parameters.
| Parameter | Correlation coefficient with DPP | Parameter | Correlation coefficient with DPP |
|---|---|---|---|
| Reservoir temperature | 0.483 | C7+ mole fraction | 0.283 |
| C1 mole fraction | 0.229 | N2 mole fraction | -0.124 |
| C2 mole fraction | -0.115 | CO2 mole fraction | 0.006 |
| C3 mole fraction | -0.195 | H2S mole fraction | -0.105 |
| C4 mole fraction | -0.275 | C7+ relative density | 0.423 |
| C5 mole fraction | -0.310 | C7+ relative mo- lecular weight | 0.776 |
| C6 mole fraction | -0.264 |
The initial equation was adjusted by changing the grouped components and/or adding new parameters. After evaluating several regression scenarios and testing many possible combinations, the final correlation was obtained and is expressed as Equation (2).
where
$I_{1}=B_{1}+B_{2}(1.8T+32)$
$I_{2}=B_{3}F_{C_{1}}+B_{4}(F_{C_{2}}+F_{C_{3}})+B_{5}F_{C_{4}}+B_{6}(F_{C_{5}}+F_{C_{6}})$
$I_{3}=B_{7}F_{CO_{2}}+B_{8}F_{H_{2}S}+B_{9}F_{N_{2}}$
$I_{4}=B_{10}(\gamma_{C_{7+}}M_{C_{7+}})+B_{11}(F_{C_{7+}}\gamma_{C_{7+}}M_{C_{7+}})+B_{12}\frac{M_{C{7+}}}{\gamma_{C{7+}}+0.00001}+B_{13}\lgroup\frac{M_{C{7+}}}{\gamma_{C{7+}}+0.00001}\rgroup$
$I_{5}=B_{14}\frac{F_{C_{1}}}{F_{C_{7+}}+0.00001}+B_{15}\frac{F_{C_{1}}}{I_{2}-B_{3}F_{C_{1}}}+B_{16}\frac{M_{C_{7+}}}{F_{C_{2}}+F_{C_{3}}+F_{C_{4}}+F_{C_{5}}}$
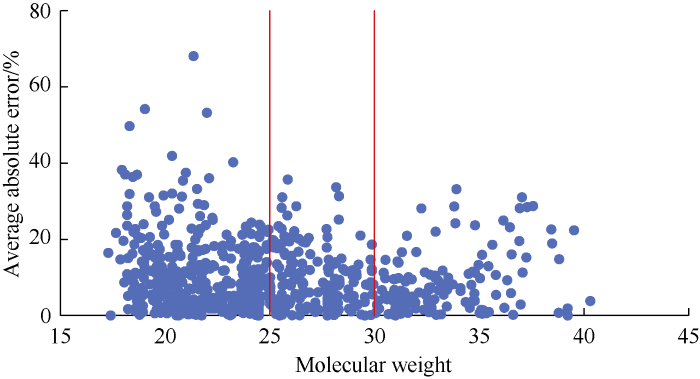
It can be seen from Fig. 5 that the error tends to decrease with the increase of total molecular weight, except some scattering abnormal points. Samples with a relative molecular weight less than 25 and higher than 30 have errors of high dispersion.
Fig. 5.
Fig. 5.
Average absolute error (AAE) versus relative molecular weight (MWt) of the new correlation before grouping the dataset.
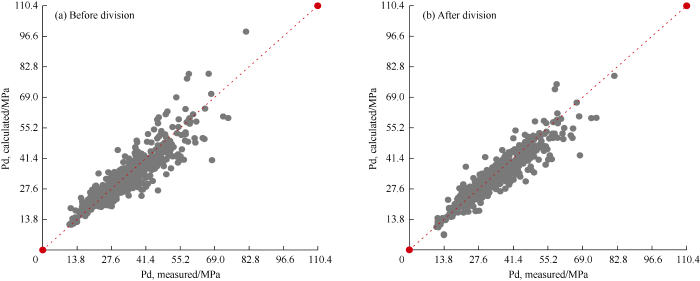
The correlation can be improved if the data set is divided into three groups based on the total molecular weight: the first with relative molecular weight below 25, the second between 25 and 30, and the third greater than 30. It can be seen from Table 12 and Fig. 6 that after regrouping, the new correlation improves significantly in accuracy, with AAE reducing from 10.03% to 7.58%, RMSE dropping from 705 to 588, and R2 increasing from 0.81 to 0.87. After regrouping, the correlation is the same as equation 2 in structure, only the coefficients were refitted (Table 13).
Table 12 Statistical parameters of the new correlation before and after regrouping the dataset.
| Condition | AAE/ % | Max AE/ % | Min AE/ % | ARE/ % | RMSE | R2 |
|---|---|---|---|---|---|---|
| Before regrouping | 10.03 | 68.06 | 0 | -0.62 | 705 | 0.81 |
| After | 7.58 | 48.90 | 0 | -1.31 | 588 | 0.87 |
Fig. 6.
Fig. 6.
Cross plots of the calculated DPPs with the new correlation before and after dividing the dataset and experimental DPPs.
Table 13 Refitted coefficients of the new correlation after regrouping the dataset.
| Coefficient | Fitted value of the coefficients | ||
|---|---|---|---|
| The group with relative molecular weight of less than 25 | The group with relative molecular weight of 25-30 | The group with relative molecular weight of more than 30 | |
| B1 | 2089.21 | -1693.97 | -898.81 |
| B2 | -0.295 4 | 0.603 4 | 0.301 3 |
| B3 | 2402.75 | 6190.56 | 4822.22 |
| B4 | -407.29 | -242.33 | -1.43 |
| B5 | -26905.44 | 1913.25 | -2.26 |
| B6 | -2451.66 | 6851.58 | -6.71 |
| B7 | -607.18 | -4593.62 | 4046.66 |
| B8 | -2020.02 | 2385.59 | 3683.02 |
| B9 | 2443.30 | 10489.60 | 7935.42 |
| B10 | 79.41 | 84.71 | 63.82 |
| B11 | 428.70 | 87.66 | 43.70 |
| B12 | -74.98 | -77.91 | -54.22 |
| B13 | 0.136 6 | 0.149 0 | 0.099 1 |
| B14 | -0.014 5 | -0.021 5 | -0.017 3 |
| B15 | 206236.66 | 95999.67 | -857.83 |
| B16 | 0.242 8 | -0.029 3 | -0.766 5 |
5. Comparison of the new correlation with published correlations
5.1. Statistical comparison
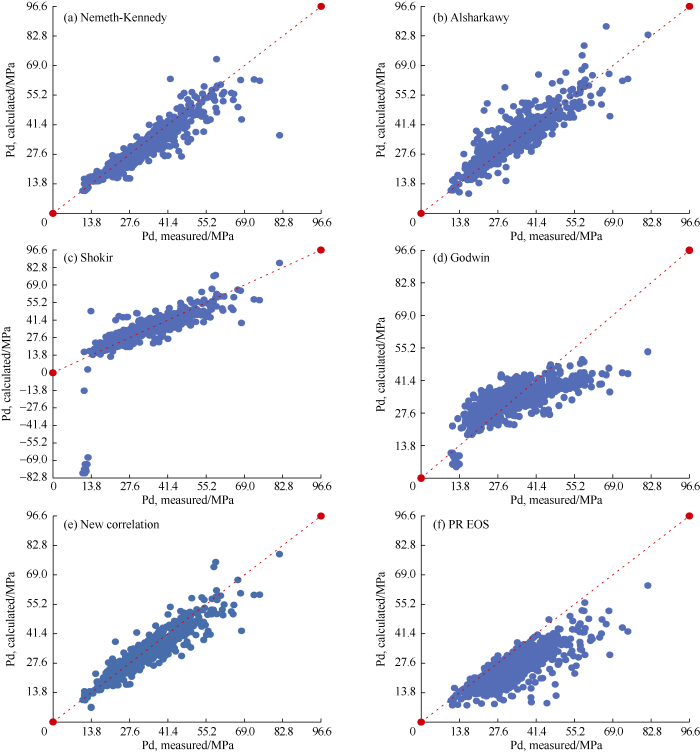
The statistical parameters of the four published correlations in Table 10 were compared with the statistical parameters of the new correlation after regrouping of the dataset in Table 12, and the results show that the new correlation has the highest accuracy. By making cross plots of the experimental and calculated DPPs (Fig. 7), we also found that the DPP values calculated with the new correlation match best with the experimental DPP values. Because the new correlation divides the dataset into three groups based on the total molecular weight, it is necessary to compare its performance with the published correlations by each group of the dataset. It can be seen from Table 14, for the first group (MWt < 25 lb./lb.-mole), the new correlation resulted in the lowest AAE and highest R2. For the second group (25 lb./lb.-mole < MWt < 30 lb./lb.-mole), the new correlation resulted in the lowest AAE (7.2%), while the Nemeth and Kennedy correlation resulted in the highest R2 (0.89). Finally, for the third group (MWt > 30 lb./lb.-mole), results from the new correlation had the lowest AAE and highest R2.
Fig. 7.
Fig. 7.
Cross plots of experimental and calculated DPPs.
Table 14 Comparison of the new correlation after dataset regrouping with all the other correlations considered in this study.
| Relative molecular weight | Correlation | AAE/% | R2 |
|---|---|---|---|
| <25 | Nemeth-Kennedy | 9.700 | 0.810 |
| Elsharkawy | 16.370 | 0.637 | |
| Shokir | 13.605 | 0.609 | |
| Godwin | 20.146 | 0.514 | |
| New correlation | 8.815 | 0.847 | |
| 25-30 | Nemeth-Kennedy | 8.295 | 0.890 |
| Elsharkawy | 8.688 | 0.872 | |
| Shokir | 49.812 | -2.848 | |
| Godwin | 18.858 | 0.612 | |
| New correlation | 7.209 | 0.867 | |
| >30 | Nemeth-Kennedy | 6.951 | 0.782 |
| Elsharkawy | 7.343 | 0.897 | |
| Shokir | 37.055 | -1.620 | |
| Godwin | 19.180 | 0.485 | |
| New correlation | 4.769 | 0.933 |
5.2. Sensitivity of the correlations to different input parameters
After statistical evaluation, the sensitivity of the published correlations and the new proposed correlation to parameters such as temperature, methane mole fraction, heptane-plus mole fraction, and molecular weight of heptane plus were analyzed.
5.2.1. Sensitivity to temperature
For the dataset in the study, many samples were experimentally tested at several temperatures. The correlations and the untuned Peng-Robinson EOS were applied to these samples, and the predicted trends of DPP vs. temperature were compared with those of experimental data. Two samples (samples 13 and 14) were selected to illustrate temperature sensitivity of the correlations. Table 15 shows the compositions of these two samples.
Table 15 Samples used for temperature sensitivity analysis.
| Sample No. | Mole fraction of each component/% | C7+ relative molecular weight | C7+ relative density | Relative molecular weight | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | ||||
| 13[13] | 85.35 | 4.77 | 2.39 | 1.08 | 0.59 | 0.46 | 1.09 | 4.17 | 0.10 | 0 | 123.0 | 0.754 9 | 20.18 |
| 14 | 83.16 | 4.79 | 2.22 | 1.50 | 1.03 | 1.06 | 3.17 | 1.99 | 1.08 | 0 | 139.9 | 0.740 0 | 23.75 |
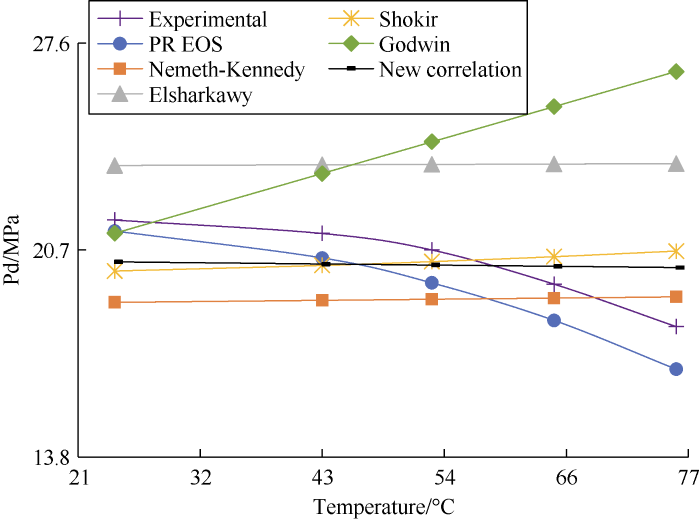
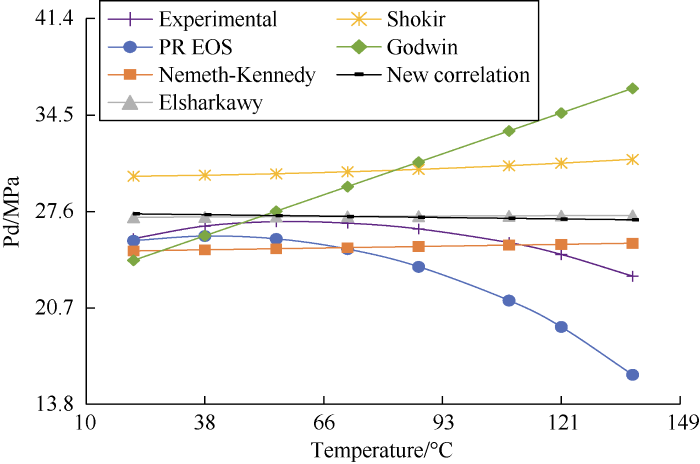
On a typical gas condensate phase envelope, the DPP increases with temperature until the cricondenbar value is reached, then it starts decreasing. Fig. 8 shows the tested DPP and the DPP calculated with the untuned PR EOS both have a clear decreasing trend as the temperature increases. The DPP values calculated by the new correlation show a slight decrease. The DPP values calculated by Nemeth and Kennedy, Elsharkawy, and Shokir correlations show a slight increase as the temperature increases. The DPP values calculated by Godwin correlation show a relatively sharp increase with the increase in temperature. Therefore, all the correlations fail to capture the actual variation trend of DPP with temperature.
Fig. 8.
Fig. 8.
Temperature sensitivity analysis results of sample 13.
Fig. 9 show that as temperature increases, the DPP tested by experiment and DPP calculated by untuned PR EOS increase to a maximum value (the temperature at the cricondenbar) and then start to decrease. All the correlations are unable to capture the actual trend of DPP with temperature. Therefore, we do not recommend the use of any DPP correlation to construct the phase envelope for a gas condensate reservoir.
Fig. 9.
Fig. 9.
Temperature sensitivity analysis results of sample 14.
Both Figs. 8 and 9 show that the DPP calculated by the new correlation has a slight decrease trend as temperature increases, which is what we expected, because the temperature is negatively correlated with the DPP for some samples, as shown by Equation (2) and Table 13 (B2 is negative). Although the decreasing trend in the figures is minor, the new correlation is the only one to reflect it.
5.2.2. Sensitivity to mole fractions of C1 and C7+
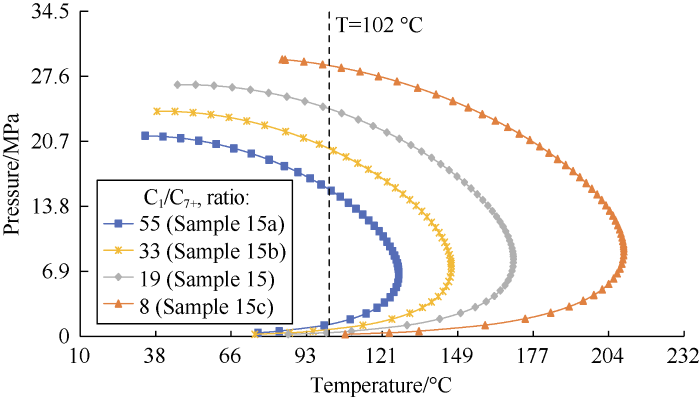
No experimental data in the dataset shows the sensitivity of DPP to variations of the C1 and C7+ mole fractions. In this study, several synthetic samples were generated by changing the C1/C7+ mole ratio of an original sample. Sample 15 was selected to analyze sensitivity of the correlations to methane and heptane-plus mole fractions. The compositions of the original sample (sample 15) and the synthetic samples (sample 15a, 15b and 15c) are shown in Table 16. Only the original sample has one experimental DPP; therefore, the variation trend of DPP with C1 and C7+ mole fractions predicted by the EOS was taken as a reference. The PVTi software was used to generate phase envelopes for the samples in Table 16. The dew point lines of these samples are shown in Fig. 10. It can be seen the reservoir temperature line intersects with the dew point lines of all samples; and with the increase of C1 and C7+ mole fractions, the phase envelops contract and move toward left.
Table 16 Samples used for the sensitivity analysis of methane and heptane-plus mole fractions.
| Sample No. | Reservoir temperature/°C | Mole fraction of each component/% | C7+ relative density | C7+ relative molecular weight | C1/C7+ mole ratio | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7+ | N2 | CO2 | H2S | |||||
| 15a | 102 | 84.0 | 4.8 | 2.3 | 1.7 | 1.3 | 1.4 | 1.5 | 1.9 | 1.1 | 0 | 0.74 | 139.9 | 55.336 |
| 15b | 102 | 83.0 | 4.8 | 2.3 | 1.7 | 1.3 | 1.4 | 2.5 | 1.9 | 1.1 | 0 | 0.74 | 139.9 | 32.963 |
| 15[13] | 102 | 81.2 | 4.8 | 2.3 | 1.7 | 1.3 | 1.4 | 4.3 | 1.9 | 1.1 | 0 | 0.74 | 139.9 | 19.108 |
| 15c | 102 | 76.0 | 4.8 | 2.3 | 1.7 | 1.3 | 1.4 | 9.5 | 1.9 | 1.1 | 0 | 0.74 | 139.9 | 7.985 |
Fig. 10.
Fig. 10.
DPP lines of samples with different C1/C7+ mole ratios predicted by the Peng-Robinson EOS.
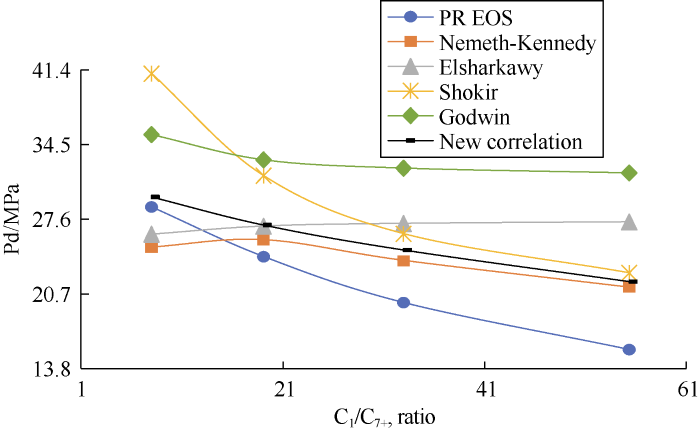
Fig. 11 shows the DPP calculated by PR EOS decreases with the increase of C1/C7+ mole ratio. The Nemeth and Kennedy, Shokir, and Godwin correlations, as well as the new correlation, capture this trend, whereas the Elsharkawy correlation results in an opposite trend.
Fig. 11.
Fig. 11.
Results of sensitivity analysis of methane and heptane- plus mole fractions.
5.2.3. Sensitivity to C7+ molecular weight
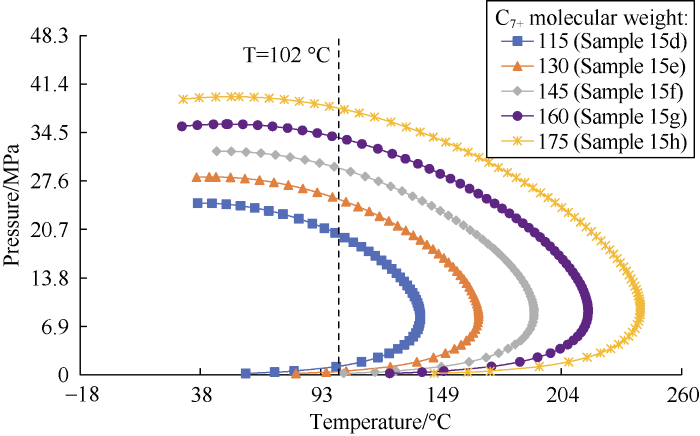
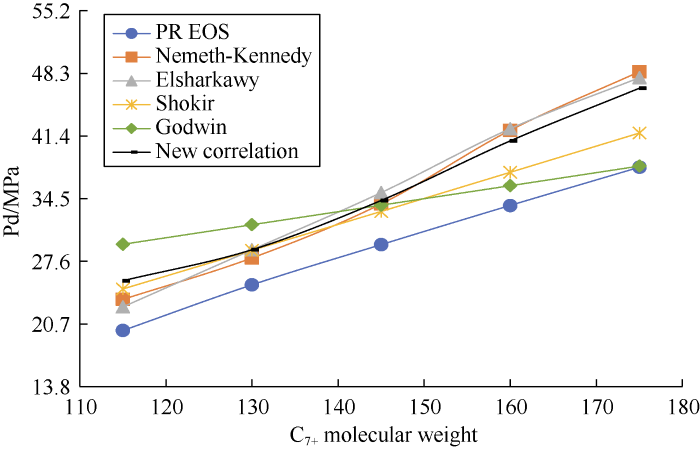
The sensitivity of the DPP predicted by the correlations to the molecular weight of C7+ was analyzed by varying the C7+ molecular weight of Sample 15 and generating 5 synthetic samples (with no change in composition). Fig. 12 shows the dew-point lines of the samples. According to this figure, as MWC7+ increases, the phase envelope becomes flatter and shifts toward the right.
Fig. 12.
Fig. 12.
Dew-point lines of the synthetic samples with different MWC7+ generated by the Peng-Robinson EOS.
Fig. 13 shows that the DPP values calculated by the four correlations, the new correlation and the PR EOS tend to increase with the increase of molecular weight of C7+.
Fig. 13.
Fig. 13.
Analysis of sensitivity to the molecular weight of heptane plus.
6. Conclusions
Gas condensate samples measured experimentally and collected from literatures were screened rigidly to remove the defective and unreliable ones. It is found during the screening that the industrial standards for identifying gas condensate reservoirs based on relative molecular weight and heptane plus content are not accurate. Four previously published empirical correlations, the Nemeth and Kennedy, Elsharkawy, Shokir, and Godwin correlations, as well as the untuned Peng-Robinson EOS, were applied to the filtered dataset to test their accuracy. The results show that the Nemeth and Kennedy correlation is the most accurate, followed by the Elsharkawy and Godwin correlations.
The Shokir correlation has the lowest accuracy because it cannot be used to samples with no C7+ components. DPP calculated by EOS is not unique and not necessarily accurate. The four previous correlations were modified, and a new correlation was worked out based on the data bank collected. The new correlation is better than the former four correlations according to statistics.
The sensitivity analysis results show that the PR EOS can reflect the variation trend of DPP with reservoir temperature, while all correlations cannot. The PR EOS, and Nemeth and Kennedy, Shokir, and Godwin correlations can reflect the decrease trend of DPP with the increase of C1/C7+, while the Elsharkawy correlation cannot. The PR EOS and all the correlations can reflect the increase trend of DPP with the increase of C7+ relative molecular weight.
Finally, a new correlation was presented based on the large data bank. The new correlation yields an AAE of 7.5% and a correlation coefficient of 0.87, which is statistically superior to all other published correlations. Moreover, the new correlation successfully captured the physical trends in DPP when the temperature, C1/C7+, and molecular weight of the heptane plus fraction were varied.
Nomenclature
A1—A10, B1—B16—coefficient;
FC1—FC6—mole fractions of C1—C6 , %;
FC7+—mole fraction of C7+, %;
FCO2—mole fraction of CO2, %;
FH2S—mole fraction of H2S, %;
FN2—mole fraction of N2, %;
MC7+—relative molecular weight of C7+;
pd—dew point pressure, MPa;
T—temperature, °C;
γC7+—relative density of C7+.
Reference
Predicting the dew point pressure for gas condensate reservoirs: Empirical models and equations of state
DOI:10.1016/S0378-3812(01)00724-5 URL [Cited within: 8]
EOS simulation and GRNN modeling of the constant volume depletion behavior of gas condensate reservoirs
DOI:10.1021/ef970135z URL [Cited within: 1]
A new cubic equation of state for reservoir fluids
DOI:10.1016/j.fluid.2005.10.013 URL [Cited within: 2]
A new cubic equation of state for fluids and fluids mixtures
DOI:10.1016/0009-2509(82)80099-7 URL [Cited within: 1]
A new two constants equation of state
DOI:10.1021/i160057a011 URL [Cited within: 3]
On the thermodynamics of solutions. V: An equation of state. Fugacities of gaseous solutions
URL PMID:18125401 [Cited within: 1]
Equilibrium constants from a modified Redlich Kwong equation of state
DOI:10.1016/0009-2509(72)80096-4 URL [Cited within: 1]
Applications of equations of state in the oil and gas industry: MORENO J C. Thermodynamics-kinetics of dynamic systems
Prediction of gas condensate properties by Esmaeilzadeh-Roshanfekr equation of state
Critical properties of volatile hydrocarbon mixtures. Trans
A correlation of dewpoint pressures with fluid composition and temperature
Volumetric and phase behavior of oil and gas from Paloma Field
Prediction of saturation pressures for condensate-gas and volatile oil mixtures
Volumetric and viscosity studies of oil and gas from a San Joaquin valley Field
Volumetric behavior of oil and gas from Louisiana Field
PVT and phase behavior of petroleum reservoir fluids
Gas production operations
5th ed.
Equations of state and PVT analysis
Dewpoint pressure model for gas condensate reservoirs based on genetic programming
Calculating viscosities of reservoir fluids from their compositions
Phase equilibria and separation process. Lyngby, Denmark: Institute for Kemiteknik,
Improved prediction of enthalpy of fractions
Characterization parameters for petroleum fractions
Physical data for distillation correlations: Vapor-liquid equilibrium: Proceedings of the 27th Meeting
Simplified monographic presentation, characterization of petroleum fractions
Applied hydrocarbon thermodynamics. Part 4. Compressibility factors and equations of state