Introduction
Microscale gas flow simulation research has greatly promoted scientific and technological progress and profoundly affected development in fields such as micro-electromechanical systems (MEMS), biopharmaceuticals, instrumentation, semiconductor materials, and aerospace[1,2]. In recent years, the efficient development of unconventional natural gas resources such as shale gas, coalbed methane, and tight sandstone gas has attracted wide attention. As this kind of reservoir rock is tight, gas flow spaces in them are mostly micro-nano meter channels, and the flow mechanisms of gas in them are complex[3,4,5,6,7], conventional physical experiments and numerical simulation methods cannot reveal the details of microscale gas flow in them. Hence, researchers began to use microscale simulation technology to simulate the flow of unconventional natural gas[7,8,9,10,11].
In the micro-nano channel, the number of gas molecules is too small to support the continuum hypothesis. What’s more, there is compression effect and slippage phenomenon in the process of gas flow, and the boundary Knudsen layer near the wall surface also has an important influence on the flow, endowing the microscale gas flow with characteristics different from the conventional macroscale flow. The Knudsen number (Kn), as the control parameter of gas flow characteristics, is defined as the ratio of the mean free path of the gas molecule to the flow characteristic length. According to Kn, gas flow can be divided into continuum flow (Kn≤0.001), slip flow (0.001<Kn≤0.1), transition flow (0.1<Kn≤10), and free molecular flow (Kn>10)[12]. In the continuum flow regime, the continuum hypothesis holds, and the gas flow satisfies the Navier-Stokes equation. In the slip flow regime, the continuum hypothesis is basically valid, and the Navier-Stokes equation considering the boundary slip correction is regarded as a feasible method for simula-tion[13,14,15]. In the transition flow regime, the continuum hypothesis fails, and the gas flow can be described by the Burnett equation. In the free molecular flow regime, the molecular dynamics method is usually used in flow simulation. In the microscale complex flow system, the channels vary widely in size, so all the above flow states may exist simultaneously. In theory, the direct simulation Monte Carlo (DSMC) method and molecular dynamics method can simulate all flow states, but their computational cost is too high. Considering the applicable conditions of different simulation methods, some researchers adopted different methods for coupling calculations of mixed flow. However, such methods are difficult and complicated, and the accuracy of the simulation results is not guaranteed. Hence, the lattice Boltzmann method (LBM) may be a good choice for simulating fluid flow and transport phenomenon[7-8, 16]. Different from the traditional computational fluid dynamics method, the lattice Boltzmann method is based on microscopic particles and mesodynamic equations, has a clear physical background, is easily programmable, and has natural parallelism. Moreover, it can address complex boundaries and has great advantages in studying microscale unconventional natural gas flow, so it has been widely used[11, 16-27].
When the lattice Boltzmann method is adopted to simulate microscale gas flow, the selection of dimensionless relaxation time and boundary conditions are crucial[28]. At present, the relationship between the dimensionless relaxation time and Kn is established through the derivation of molecular dynamics theory, and then Kn is used to determine the dimensionless relaxation time under simulated conditions[28,29]. As different calculation accuracy and physical parameter calculation expressions were adopted by predecessors in the formula derivation process, many relations between Kn and dimensionless relaxation time were come up[14-15, 28, 30-35], and the dimensionless relaxation time was modified by taking into account the influences of different factors[36,37,38,39,40,41,42]. All researchers deduced the expression of the dimensionless relaxation time based on the molecular dynamics theory previously, there is no report of calculating the dimensionless relaxation time by using other ideas. On the basis of previous studies, considering the similarity criterion and gas true physical property parameters, a new microscale flow simulation model suitable for unconventional natural gas under high temperature and high pressure conditions has been established in this study.
1. Microscale flow simulation model based on the LBM
1.1. Basic model theory of LBM
In 1992, Qian et al.[43] put forward the basic model of the lattice Boltzmann method, the DnQm model, which has been widely used. In the simulation of unconventional natural gas flow, the single relaxation lattice Boltzmann model with the BGK approximate collision term[44] is often adopted, which is also known as the LBGK model. The LBGK model is a special discrete form of the continuous Boltzmann-BGK equation, and the continuous Boltzmann-BGK equation is a simplification of the continuous Boltzmann equation. A complete LBGK model should include an evolution equation, an equilibrium distribution function, and a lattice model, among them, the evolution equation is expressed as follows:
In the simulation of flow in two-dimensional space, the nine-velocity discrete D2Q9 lattice model is often adopted. In this model, the equilibrium distribution function is expressed as:
where $c_{S}=\frac{c}{\sqrt{3}} \quad c=\frac{\delta X}{\delta t} \quad \rho=\sum_{i=0}^{8} f_{i}$
The momentum in the lattice space is expressed as:
In the D2Q9 lattice model, the weight coefficient $\omega_{i}$ and discrete lattice velocity c are respectively expressed as:
In addition, the kinematic viscosity and dimensionless relaxation time in the lattice space satisfies the following equation[45]:
The above kinematic viscosity treatment method gives the calculation in the LBGK model second-order accuracy. In the lattice space, the pressure of single-component single-phase gas is expressed as[28]:
The discrete expression of the force is[28]:
1.2. Dimensionless relaxation time
In the simulation of macroscopic liquid flow, the Reynolds number is usually considered as the control parameter of flow characteristics, and the dimensionless relaxation time can be determined by Reynolds number. In the simulation of microscale gas flow, Kn is the control parameter of flow characteristics, so the dimensionless relaxation time needs to be modified or redefined. Researchers have made considerable efforts in this regard before, usually the relationship between Kn and dimensionless relaxation time was established (Table 1) and then Kn was used to determine the dimensionless relaxation time. In 2002, Nie et al.[30] and Lim et al.[15] derived expressions of dimensionless relaxation time respectively.
Table 1 Relationships between the dimensionless relaxation time and Kn.
| Reference | Relational expression |
|---|---|
| Nie et al.[30] | $ \tau=1 / 2+K n H \rho / a$ |
| Lim et al.[15] | $\tau=\operatorname{Kn} N$ |
| Niu et al.[14] | $\tau=\sqrt{6 / \gamma \pi} \mathrm{Kn} \mathrm{H}$ |
| Lee et al.[31] | $\tau=1 / 2+K n N$ |
| Tang et al.[33], Zhang et al.[34] | $\tau=1 / 2+\sqrt{3 \pi / 8} \operatorname{Kn} N$ |
| Guo et al.[35] | $\tau=1 / 2+\sqrt{6 / \pi} \operatorname{Kn} N$ |
| Guo et al.[32] (The influence of Knudsen layer is considered) | $\tau=1 / 2+\sqrt{6 / \pi} \operatorname{Kn} N \psi(K n), \psi(K n)=(2 / \pi) \arctan \left(\sqrt{2} K n^{-3 / 4}\right)$ |
| Li et al.[38] (The influence of Knudsen layer is considered) | $\tau=1 / 2+\sqrt{6 / \pi} \operatorname{Kn} N \psi(K n), \psi(K n)=1 /(1+2 K n)$ |
| Zhang et al.[40] (The influence of Knudsen layer is considered) | $\tau=1 / 2+\sqrt{3 \pi / 8} \operatorname{Kn} N /\left\{1+0.7\left[\mathrm{e}^{-C y / \lambda}+\mathrm{e}^{-C(H-y) / \lambda}\right]\right\}$ |
| Tang et al.[41] (The influence of Knudsen layer is considered) | $\tau=1 / 2+\left(\lambda / \lambda_{0}\right) \sqrt{\pi / 8}\left(c / c_{\mathrm{s}}\right) \operatorname{Kn} N$ |
| Guo et al.[42] (The influence of Knudsen layer is considered) | $\tau=1 / 2+\sqrt{6 / \pi} K n N\left[1+(y / \lambda-1) \mathrm{e}^{-y / \lambda}-(y / \lambda)^{2} \operatorname{Ei}(y / \lambda)\right]$ |
But the two expressions have obvious difference. The former has the parameter "1/2", indicating that the model has second-order accuracy[28], while the latter does not. In the expression of dimensionless relaxation time deduced by Niu et al.[14], the specific heat capacity of the simulated gas is 5/3, with τ≈Kn H, and apparently this method does not have second-order calculation accuracy. According to the inference of Guo et al.[28], the dimensionless relaxation time can be expressed as $\tau=1 / 2+(c / \bar{c}) \operatorname{Kn} N$. Different literatures have different choices for the mean velocity of particles ($\overline{\mathcal{C}}$), resulting in different expressions of dimensionless relaxation time. In the expression derived by Lee et al.[31], the mean velocity of particles is selected to approximate the lattice speed, but according to the research of Guo et al.[32], this treatment method does not satisfy the consistency condition. The expressions derived by Tang et al.[33] and Zhang et al.[34] select the mean velocity of particles as $\bar{c}=\sqrt{8 R T / \pi}$. Based on the molecular dynamics theory, Guo et al.[32, 35] approximately deduced the expression of the mean velocity of particles as $\sqrt{\pi R T / 2}$, and then obtained the expression of dimensionless relaxation time. At present, researchers usually directly apply the expressions derived by Tang et al.[33], Zhang et al.[34] or Guo et al.[32, 35], or make improvements on them. For example, under the condition of high temperature and high pressure, Shi et al.[36] took into account the influence of gas denseness on gas viscosity and made corresponding corrections to the dimensionless relaxation time. In this case, the expression of dimensionless relaxation time proposed by Tang et al.[33], Zhang et al.[34] and Guo et al.[35] can be modified as $\tau=1 / 2+\sqrt{3 \pi / 8} \operatorname{Kn} N\left[1+2 b \rho_{\mathrm{r}} \chi /(D+2)\right]^{2} / \chi$ or $\tau=1 / 2+\sqrt{6 / \pi} \operatorname{Kn} N\left[1+2 b \rho_{\mathrm{r}} \chi /(D+2)\right]^{2} / \chi$, where $\chi=1+ (5 / 8) b \rho_{\mathrm{r}}+0.2869\left(b \rho_{\mathrm{r}}\right)^{2}+0.1103\left(b \rho_{\mathrm{r}}\right)^{3}+0.0386\left(b \rho_{\mathrm{r}}\right)^{4}$, and $b=2 \pi d_{\mathrm{r}}^{3} / 3 m_{\mathrm{r}}$.
In microscale flow simulation, the influence of boundary Knudsen layer should also be considered. The existence of solid wall truncates the mean free path of the gas molecule near the wall, which affects the motion law of gas molecules within a certain range (i.e. the Knudsen layer)[8, 11]. When the characteristic length of the flow channel is large, the Knudsen layer takes up a small proportion in the whole flow channel, and its influence on the flow can be ignored. However, as the characteristic length of the flow channel decreases, the proportion of Knudsen layer in the flow channel gradually increases, and its influence on the flow also increases[8], resulting in microscale flow characteristics. Therefore, the researchers modified the dimensionless relaxation time accordingly. In general, the influence of the boundary Knudsen layer is represented by modifying the mean free path of the gas molecule. Some researchers regarded the reduction of the mean free path of the gas molecules in Knudsen layer to the reduction of the mean free path of the gas molecules of the entire flow field. Stops et al.[37] proposed the correction formula $\lambda_{\mathrm{e}}=\lambda \psi(K n)$ for the mean free path of the gas molecule under two-dimensional plate flow. However, the correction coefficient $\psi(K n)$ is too complicated to be used in actual calculation. Guo et al.[32] proposed a new correction coefficient on this basis. Based on the direct proportion relationship between the dynamic viscosity and the mean free path of the gas mole-cule, Li et al.[38] used the Bosanquet-type correction coefficient proposed by Michalis et al.[39] Zhang et al.[40], Tang et al.[41] and Guo et al.[42] modified the mean free path of the gas molecule at different positions in the flow field by considering the distance between different positions and the wall surface, and deduced the corresponding dimensionless relaxation time.
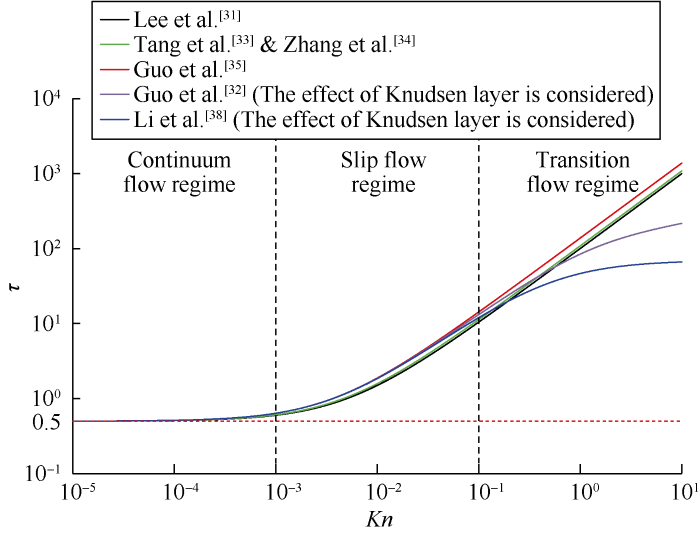
The above dimensionless relaxation time expressions are all derived from molecular dynamics theory and are widely used in microscale flow simulation. Some relationships between dimensionless relaxation time and Kn in Table 1 were drawn in Fig. 1. It can be seen that under the same mesh number and Kn, the values of dimensionless relaxation time from them have some differences, especially in the transition flow regime. The dimensionless relaxation time has a strong influence on the simulation results of microscale gas flow, and small difference in the dimensionless relaxation time may lead to differences in simulation results and deviations from the correct values.
Fig. 1.
Fig. 1.
Comparison of dimensionless relaxation time at different Kn (N=100).
According to previous studies, the relationship between the mean free path of the gas molecule, relaxation time and mean velocity of particles can be expressed as[36]:
The relationship between dynamic viscosity, pressure and relaxation time can be expressed as[32] :
When considering the correction of non-ideal gas denseness under high temperature and pressure, the dynamic viscosity can be modified as[36]:
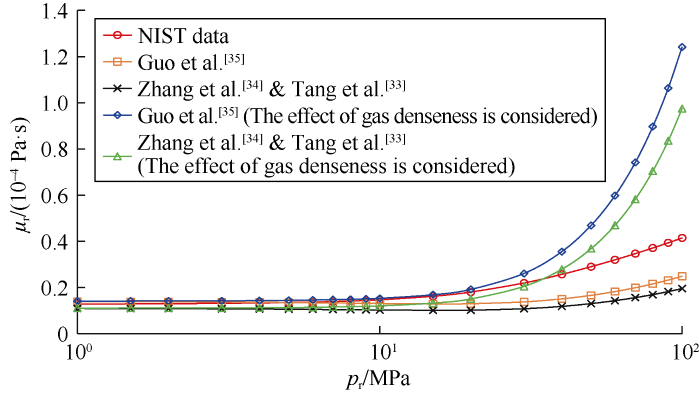
Not considering the effect of solid wall, the relationship between dynamic viscosity and pressure (1-100 MPa) of methane molecule in the real physical space corresponding to above equation (11) at 350 K was plotted (Fig. 2) and compared with the data from the National Institute of Standards and Technology (NIST) standard reference database. It can be seen from Fig. 2, when the pressure is higher than 20 MPa, the dynamic viscosities of methane molecule calculated by the expressions have considerable deviations from the data in the NIST standard reference database. That is to say, the above dimensionless relaxation time expressions can’t reflect the true situation of gas.
Fig. 2.
Fig. 2.
Variation of dynamic viscosities of methane with pressure calculated by different expressions.
In microscale flow simulation, the simulated quantities in the lattice space and real physical space should meet similarity criterion[46,47], such as Mach number, Knudsen number and Reynolds number, to truly reflect the real flow situation and reveal objective laws. In macroscopic liquid flow simulation, researchers consider that the Reynolds number under the numerical simulation conditions is the same as that under the real flow conditions, which satisfies that the ratio of inertia force to friction force in the lattice space is the same as that in the real physical space. It is worth noting that the compressibility of liquid can be ignored for macroscopic large-scale liquid flow, but for microscale gas flow, the compressibility of gas should be considered. Also, the Mach number under the simulation condition and the real flow condition should be strictly equal, that is, the ratio of the inertial force and elastic force under the two conditions should be equal.
The Reynolds number, Knudsen number, and Mach number in the lattice space are equal to that in the real physical space, which is:
Combining equations (6) and (12)-(14), the following expression can be obtained:
Substituting $\lambda=\operatorname{Kn} H, \quad H=N \delta_{X}$ and $c_{\mathrm{s}}=\frac{c}{\sqrt{3}}$ into
equation (15), we can get:
The mean free path of the gas molecule in the real physical space is calculated by:
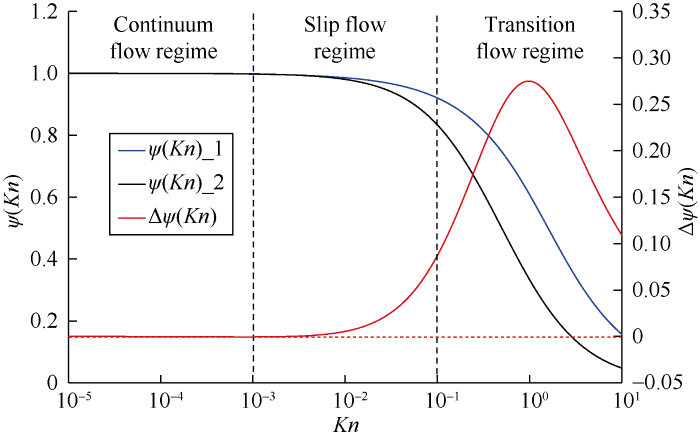
To facilitate the simulation calculation, $\psi(K n)= (2 / \pi) \arctan \left(\sqrt{2} K n^{-3 / 4}\right)$ proposed by Guo et al.[32] or $\psi(K n)=1 /(1+2 K n)$ proposed by Michalis et al.[39] is considered as ψ(Kn)_1 and ψ(Kn)_2 respectively, for the correction coefficient ψ(Kn) in the above equation. The calculated values of the above two correction coefficients within the range of 1×10-5-10 are plotted in Fig. 3. It can be seen that there are obvious differences between the two correction coefficients. In the continuum flow regime, the two correction coefficients basically remain unchanged, and ψ(Kn)_1≈ψ(Kn)_2≈1.0. In the slip flow and transition flow regimes, the correction coefficients begin to drop, and the falling speed first increases and then decreases. The difference between the correction coefficients mainly occurs in the slip flow and transition flow regimes, and ψ(Kn)_1>ψ(Kn)_2 in these two regimes. If we define $\Delta \psi(K n)=\psi(K n)_{-} 1-\psi(K n)_{-} 2$, it can be seen that there is a maximum difference Δψ(Kn)max near Kn≈1.0. Since the gas kinematic viscosity in equation (18) can be queried from the NIST standard reference database based on temperature and pressure, there is no need to modify the gas denseness separately. As slight difference in the dimensionless relaxation time will lead to significant difference in simulation results, affecting whether the flow simulation can correctly capture physical phenomena at microscale, so the correction coefficient for dimensionless relaxation time needs to be optimized.
Fig. 3.
Fig. 3.
Values and differences of correction coefficients under different Knudsen numbers.
1.3. Boundary conditions and key parameters
In micro-scale simulation, when periodic gas flow in a microchannel is considered, the periodic boundary condition is usually adopted at the inlet and outlet of the microchannel[47]. When gas flows in a microchannel driven by the inlet and outlet pressure difference, the pressure boundary condition proposed by Zou et al.[48] or the nonequilibrium extrapolation boundary condition proposed by Guo et al.[49] can be adopted at the inlet and outlet. In comparison, the boundary conditions at the upper and lower walls of the microchannel are more difficult to handle. By using reasonable boundary conditions at the wall surface, phenomena such as boundary slippage can be effectively captured.
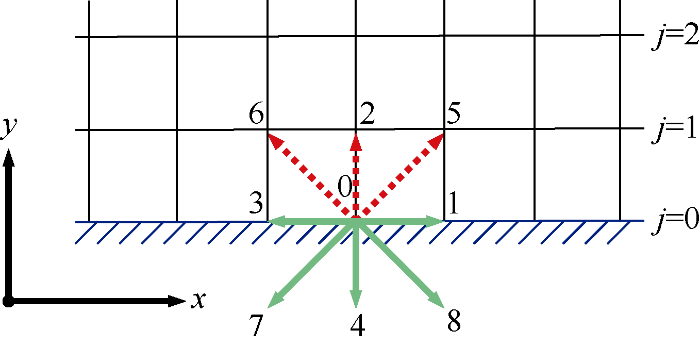
Researchers usually adopt two kinds of boundary conditions when addressing microscale gas flow[7, 35], i.e., the combined bounce-back/specular-reflection (CBBSR) boundary condition and discrete Maxwell (DM) boundary condition. The above two boundary conditions are equivalent in essence, and the CBBSR boundary condition is adopted in this paper[35]. Take the lower boundary of the two-dimensional microchannel as an example, the grid division is shown in Fig. 4. In this paper, setting the grid nodes at the position of the wall boundary can directly capture the boundary slip velocity. After the collision and migration steps, the unknown particle distribution functions f2, f5, and f6 can be obtained as follows:
Fig. 4.
Fig. 4.
Schematic diagram of the grid division (The number represents the direction of the discrete velocity).
In microscale flow simulation, the value of combination coefficient r directly affects the boundary slip velocity obtained by the simulation, and the differences in simulation conditions cannot be reflected if r is set as a fixed value[50]. To eliminate the effect of numerical discreteness and make the simulation meet the second-order slip boundary condition, the expression for the combination coefficient can be derived according to the theory of Guo et al.[35] and the dimensionless relaxation time proposed in this paper as:
Guo et al.[51] give the following expression in the generalized second-order slip boundary condition:
$ A_{1}=\frac{2-\sigma}{\sigma}(1-0.1817 \sigma) \quad A_{2}=\sigma^{2}\left(\frac{1}{\pi}+\frac{1}{2} A_{1}^{2}\right)$
where $ \sigma=\left(2-\sigma_{\mathrm{v}}\right) / \sigma_{\mathrm{v}}$
2. Validation of the model
2.1. Simulation of gas flow in a microchannel with infinite length
First, the flow of methane driven by the body force in a microchannel with infinite length under isothermal conditions was simulated to verify the model. Gas flow in the microchannel can be equivalent to flow in an infinite long microchannel by setting periodic boundary condition at the inlet and outlet[47]. In general, the pressure gradient is considered as a small constant[38], and the external force term in the entire flow field is unified As $ \boldsymbol{F}=\left(F_{X}, F_{y}\right)$. In this work, Fx was 10-6 and Fy was 0. In this case, the gas pressure changes very little along the flow direction. Thus the macroscopic physical property parameters difference of the gas can be ignored. The dimensionless relaxation time in the whole flow field was set as constant, and the effect of compression could be ignored. Only the slippage effect of the gas and the influence of the boundary Knudsen layer need to be considered. The grid was divided as Nx×Ny=30×300. Due to the use of periodic flow boundary condition, the number of grids in the flow direction (i.e., x-direction) was less. All the physical property parameters of methane involved in equations (18) and (20) were obtained from the NIST standard reference database. Different Kn values and its corresponding dimensionless relaxation time and combination coefficients were obtained by changing the spacing (Hr) between the upper and lower wall surfaces of the simulated microchannel. As the flow under high Kn needed to be simulated, in order to ensure that the channel characteristic length is nano-scale, the simulated pressure should not be too high, so the Tr and the pr were set as 400 K and 0.1 MPa, respectively.
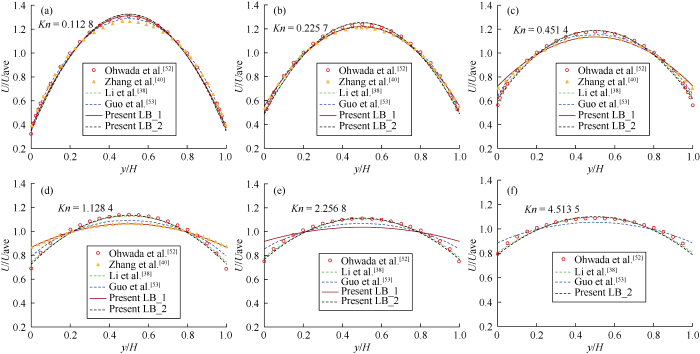
Ohwada et al.[52] simulated the gas flow in a two-dimensional microchannel by directly solving the linearized Boltzmann equation, and researchers usually use their results to verify the accuracy of microscale flow models[38, 40, 51, 53]. The model proposed in this paper was used for simulation to obtain the dimensionless velocity profiles U/Uave at the outlet with different Kn values, where $ U_{\text {ave }}=(1 / H) \int_{0}^{H} U \mathrm{~d} y$. When different correction coefficients ψ(Kn)_1 and ψ(Kn)_2 were adopted, the corresponding simulation results were marked as "Present LB_1" and "Present LB_2", respectively. The simulation results were compared with those of Ohwada et al. to verify the model accuracy and optimize the correction coefficient. Meanwhile, the simulation results were also compared with the simulation results of Zhang et al.[40], Li et al.[38] and Guo et al.[53] (Fig. 5).
Fig. 5.
Fig. 5.
Dimensionless velocity profiles at the outlet of the methane flowing in the microchannel periodically.
It can be seen from Fig. 5, the calculation accuracy of the model in this paper varies with Kn when $ \psi(K n)=\psi(K n)_{-} 1$. When Kn=0.112 8, the simulation results of the model presented in this paper are consistent with those obtained by Ohwada et al. from directly solving the linearized Boltzmann equation. However, the dimensionless velocity calculated by the model in this paper at the center line position is greater than those of Zhang et al. and Guo et al. With the increase of Kn, the simulation results of the model in this paper gradually deviate from the results of Ohwada et al., specifically, the dimensionless velocity at the boundary is larger, while the dimensionless velocity in the middle of the channel is smaller, presenting a good consistency with the calculated results of Zhang et al. It is worth noting that when $Kn>2.5$, the simulation does not converge. When $\psi(K n)=\psi(K n)_{-} 2$, the simulation results of the model in this paper are always in consistent with the simulation results of Ohwada et al., indicating that the model has a higher calculation accuracy and can effectively capture the microscale gas flow boundary slippage phenomenon within a larger variation range of Kn. In addition, the simulation results in this paper have a high consistency with the simulation results of Li et al. (Li et al. used the same correction coefficient $\psi(K n)_{-} 2$), indicating that the $\psi(K n)=\psi(K n)_{-} 1$ has an important influence on the accurate capture of boundary slip velocity. There is always a deviation between the simulation results of the model in this paper and those of Guo et al., and the deviation is very obvious when Kn is relatively large. With the increase of Kn, the boundary slip velocity increases significantly, and the effect of slippage on gas flow becomes more and more obvious.
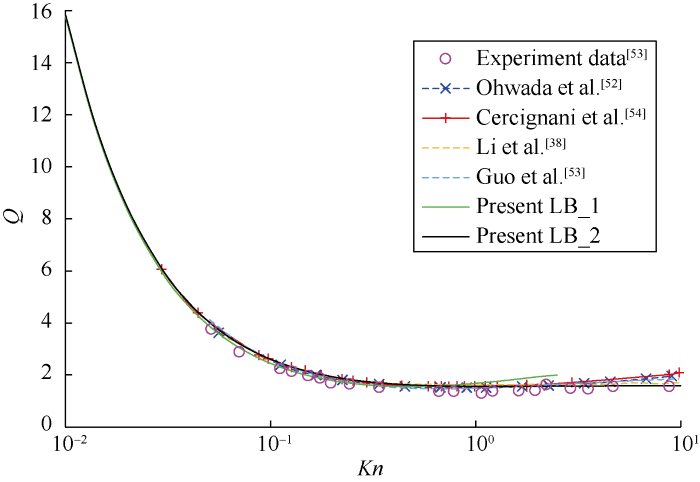
To further verify the correctness of the model in this paper and optimize the correction coefficient, the dimen-
sionless flow rates[38] $Q=\int_{0}^{H} u \mathrm{~d} y /\left(F_{X} H^{2} \sqrt{R T / 2} / p\right)$ in the microchannel under different Kn were calculated, and the simulation results were compared with the data in the literatures (Fig. 6). It can be seen that when $\psi(K n)= \psi(K n)_{-} 1$ and $Kn<1.0$, the simulation results of the model in this paper are highly consistent with the simulation results of Ohwada et al.[52], Cercignani et al.[54], Li et al.[38] and the experimental data of real gas flow[53]. However, with the increase of Kn, the simulation results of the model in this paper gradually increase and deviate from the simulation results in the above literatures. Moreover, when $Kn>2.5$, the simulation does not converge. When $\psi(K n)=\psi(K n)_{-} 2$, the simulation results of the model in this paper are in good agreement with the simulation results and experimental data in the above literatures within the whole range of Kn, thus verifying the correctness of the model. By comparing the simulation results under different correction coefficients, it can be seen that using correction coefficient $\psi(K n)=\psi(K n)_{-} 2$ can make the model in this paper higher in calculation accuracy and wider in application range.
Fig. 6.
Fig. 6.
Dimensionless flow rates of the methane flowing in the microchannel periodically with Kn.
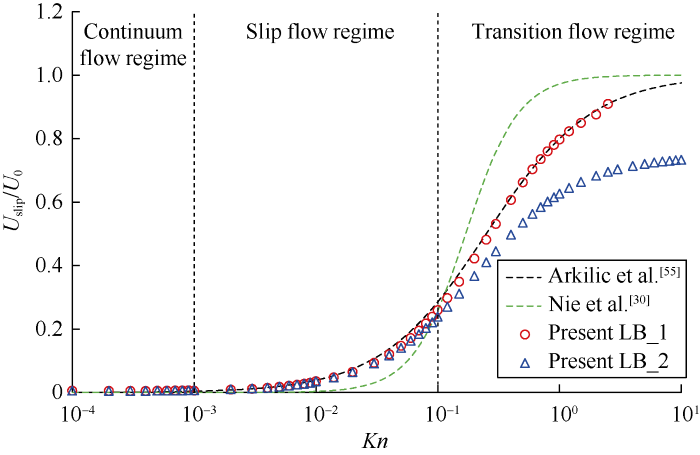
With the above two correction coefficients, the normalized boundary slip velocities $U_{\text {slip }} / U_{0}$ at the outlet of the microchannel under different Kn were calculated, and the simulation results were compared with the analytical solutions obtained by Arkilic et al.[55] considering the first-order slip boundary condition and the results obtained by Nie et al.[30] (Fig. 7). It can be seen from Fig. 7 that the simulation results obtained by adopting the two correction coefficients are similar in the slip flow regime, and the gap between them gradually turns up with the increase of Kn. In the transition flow regime, the difference between them increases further. What’s more, when $\psi(K n)=\psi(K n)_{-} 1$, the simulation results of the model in this paper have better consistency with the analytical solutions of Arkilic et al., within the whole range of Kn. In fact, only first-order slip boundary condition is considered in the derivation process of Arkilic et al., so when $\psi(K n)_{-} 1$ is adopted, the model presented in this paper only has first-order calculation accuracy. In the study of Nie et al., simple bounce-back boundary condition is adopted. It can be seen that in the slip flow regime, the simulation results of Nie et al. are smaller than the results of the other three models, while in the transition flow regime it is the opposite. When $\psi(K n)=\psi(K n)_{-} 2$, the simulation results of the model in this paper are smaller than the other three results in the transition flow regime, indicating that the adoption of $\psi(K n)_{-} 1$ results in the calculated boundary slip velocity larger than the actual boundary slip velocity in the transition flow regime.
Fig. 7.
Fig. 7.
Variation of normalized boundary slip velocities of the methane flowing in the microchannel periodically with Kn.
2.2. Gas flow in a long microchannel driven by pressure difference
Next, the model in this paper was used to simulate the methane flow driven by the pressure difference between the inlet and outlet in a long microchannel. For microscale gas flow, the temperature and pressure change slightly within the study range, and the gas flow velocity is slow, representing typical low Mach number flow. Although microscale gas flow can be regarded as incompressible in theory, compressibility exists objectively on the whole macroscopic scale, and there must be errors in the simulation ignoring compression effect. When studying such problems, all the impacts of compression effect, slippage effect and of boundary Knudsen layer should be considered. Due to the compressibility of gas, the pressure distribution along the flow direction in the microchannel is nonlinear. The simulation results in this paper were compared with the calculation results of the DSMC and information preservation-DSMC (IP-DSMC) methods, the LBM simulation results of Li et al.[38], Guo et al.[53] and Shen et al.[56], and the analytical solutions of Arkilic et al.[55] to verify the accuracy of the model. In the above literatures, the inlet/outlet pressure ratio is 1.4∶1.0 or 2.0∶1.0. Considering that the simulated pressure gradient can’t be too large, the outlet pressure was set at 0.01 MPa and the simulated temperature was kept constant at 400 K. Flow simulations under different Kn were realized by changing the space between upper and lower walls of the microchannel. As the pressure changes along the direction of the flow passage, the macroscopic physical property parameters of methane in the whole flow field will also change accordingly. According to equations (18) and (20), it can be seen that the dimensionless relaxation time, Kn and combination coefficient at different positions are different, and the variations of them with position need to be considered in simulation. The Kn at any point in the flow field is expressed as $\operatorname{Kn}(x, y)=K n_{\text {out }} \rho_{\text {out }} / \rho(X, y)$. It is worth noting that $v_{\mathrm{r}} / c_{\mathrm{sr}}$ isinvolved in the calculation of dimensionless relaxation time and combination coefficient, and corresponding pretreatments are required. By inquiring in the NIST standard reference database, a series of discrete values of $v_{\mathrm{r}} / c_{\mathrm{sr}}$ and $\rho_{\mathrm{r}}$ within the range of the inlet and outlet pressure were obtained, and then the relationship between them was fitted as $v_{\mathrm{r}} / c_{\mathrm{sr}}$=3×10-8/ρr. In the actual simulation, the density in the lattice space was set equal to that in the real physical space numerically, and then the dimensionless relaxation time and the combination coefficient at any position were calculated by using the above relation.
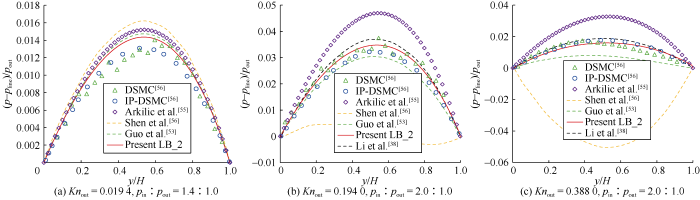
Setting $\psi(K n)=\psi(K n)_{-} 2$, the model in this paper was used to calculate the dimensionless pressure deviation $\left(p-p_{\text {line }}\right) / p_{\text {out }}$ along the microchannel at $Kn_{\text {out }}$ of 0.019 4, 0.194 0 and 0.388 0, respectively. The grid was divided as Nx×Ny=2000×20, consistent with the reference [55].
It can be seen from Fig. 8 that the results obtained by using the model in this paper are obviously better than those obtained by Arkilic et al., Shen et al., and Guo et al., and are similar to those obtained by Li et al. But the results of the model in this paper are more consistent with those of DSMC and IP-DSMC, indicating that the model in this paper can capture the compression effect of microscale gas more accurately.
Fig. 8.
Fig. 8.
Comparison of dimensionless pressure deviation of methane flow in a long microchannel calculated by the model in this paper with other references data.
3. Conclusions
Compared with the traditional computational fluid dynamics method based on the continuum hypothesis, the lattice Boltzmann method has more advantages in microscale gas flow simulation due to its mesoscopic characteristics and natural parallelism. However, the gas viscosity recovered by the widely used lattice Boltzmann model is greatly different from the real gas viscosity under high temperature and pressure, which may lead to deviation of simulation results from the correct value.
The model in this paper can effectively characterize the slippage effect and compression effect of microscale gas, and accurately capture the influence of boundary Knudsen layer. The simulation results of the periodic flow of methane in a microchannel show that the Bosanquet-type viscosity correction coefficient proposed by Michalis et al. makes the model in this paper higher in calculation accuracy and wider in application range. This way, the dimensionless boundary slip velocity and dimensionless flow rate calculated by the model in this paper are in good agreement with the data in the literatures. The simulation results of the flow of methane driven by pressure difference between the inlet and outlet in a long microchannel show that the proposed model in this paper can effectively characterize the compression effect of microscale gas. Compared with the micro-nano scale models commonly used in literatures, this model can more accurately capture the effects of boundary slip velocity and gas compression effect.
The dimensionless relaxation time expression proposed in this paper includes not only the Kn but also the real kinematic viscosity, sound speed and mean free path of the gas molecule under simulated temperature and pressure conditions, so it can more comprehensively reflect the real state of unconventional natural gas in microscale flow space under reservoir conditions. In addition, combined with other boundary conditions such as adsorption/desorption and surface diffusion, the model presented in this paper can be extended to more applications.
Nomenclature
A1, A2—coefficients related to the gas-solid interactions in the second-order slip boundary condition;
a—constant;
C—empirical parameter;
c—the lattice speed;
ci—the discrete velocity in the i-direction of the lattice space;
cs—the sound speed in the lattice space;
csr—the sound speed in the real physical space, m/s;
$\bar{c}$—the mean velocity of particles in the lattice space;
D—the dimension of the simulated space;
dr—the diameter of a gas molecule in the real physical space, and dr=0.414×10-9 m is taken for methane;
F—the external force in the lattice space;
Fx—the component of the force in the x-direction of the lattice space;
Fy—the component of the force in the y-direction of the lattice space;
Fi—the discrete force in the i-direction of the lattice space;
fi(X,t)—the particle distribution function;
fi,eq(X,t)—the equilibrium particle distribution function;
$\bar{f}_{i}$—the particle distribution function at the wall node after the streaming step;
H—the characteristic length of the flow domain in the lattice space;
Hr—the characteristic length of the flow domain in the real physical space, m;
i—the discrete velocity direction, i=0, 1, …, m-1;
I—the second order unit tensor;
j—the grid number in the y-direction;
Kn—Knudsen number, dimensionless;
Knout—Knudsen number at the outlet of the microchannel, dimensionless;
m—the number of discrete velocities;
mr—the mass of the gas molecule in the real physical space, and mr=2.664×10-26 kg is taken for methane;
N—the number of grid occupied by the characteristic length;
Nx—the number of grids in the x-diretion;
Ny—the number of grids in the y-direction;
n—the dimension of space;
p—the pressure in the lattice space;
pline—the linear pressure distribution in the lattice space;
pin—the pressure at the inlet of microchannel in the lattice space;
pout—the pressure at the outlet of microchannel in the lattice space;
pr—the pressure in the real physical space, MPa;
Q—the dimensionless flow rate in the lattice space;
R—the gas constant in the lattice space;
r—the combination coefficient, which controls the ratio of the bounce-back to the specular-reflection, and 0<r<1;
T—the temperature in the lattice space;
Tr—the temperature in the real physical space, K;
t—the time in the lattice space;
U—the velocity along the fluid flow direction at the microchannel outlet in the lattice space;
Uave—the average velocity along the fluid flow direction at the outlet of microchannel in the lattice space;
Uslip—the slip velocity at the outlet of microchannel in the lattice space;
U0—the velocity at the outlet centerline of microchannel in the lattice space;
u—the macroscopic velocity vector in the lattice space;
u—the macroscopic velocity scalar in the lattice space;
ur—the velocity in the real physical space, m/s;
X—the position in the lattice space;
x—the distance from the inlet of microchannel;
y—the distance from the lower wall of microchannel;
γ—the specific heat capacity of the gas in the lattice space;
δt—the time step in the lattice space;
δx—the grid spacing in the lattice space, and usually take δx=δt;
λ—the mean free path of the gas in the lattice space;
λe—the effective mean free path of the gas in the lattice space;
λr—the mean free path of the gas in the real physical space, m;
ρ—the macroscopic density in the lattice space;
ρout—the macroscopic density at the outlet of microchannel in the lattice space;
ρr—the gas density in the real physical space, kg/m3;
ρ—momentum accommodation coefficient in the flow direction;
σv—the tangential momentum accommodation coefficient, and usually take σv=1.0;
τ—the dimensionless relaxation time;
τs—the relaxation time in the lattice space;
μ—the dynamic viscosity in the lattice space;
μr—the dynamic viscosity in the real physical space, Pa•s;
ν—the kinematic viscosity in the lattice space;
$V_{\mathrm{r}}$—the kinematic viscosity in the real physical space, m2/s;
ωi—the weight coefficient in the i-direction;
χ—the correction coefficient of the gas denseness, dimensionless;
ψ(Kn)—the correction coefficient of the mean free path of the gas;
Δψ(Kn)—the correction coefficient difference.
Reference
Physics and applications of microfluidics in biology
DOI:10.1146/annurev.bioeng.4.112601.125916 URL [Cited within: 1]
Recent trends in mechanical micropumps and their applications: A review
Review of micro seepage mechanisms in shale gas reservoirs
Numerical solution of fractured horizontal wells in shale gas reservoirs considering multiple transport mechanisms
DOI:10.1088/1742-2140/aa93b2 URL [Cited within: 1]
Well production performance analysis for shale gas reservoirs
Controlling factors of marine shale gas differential enrichment in southern China
A lattice Boltzmann model for simulating gas flow in kerogen pores
DOI:10.1007/s11242-014-0401-9 URL [Cited within: 4]
Microscale shale gas flow simulation based on lattice Boltzmann method
Investigation of methane adsorption and its effect on gas transport in shale matrix through microscale and mesoscale simulations
DOI:10.1016/j.ijheatmasstransfer.2016.03.039 URL [Cited within: 1]
Study on the adsorption phenomenon in shale with the combination of molecular dynamic simulation and fractal analysis
DOI:10.1142/S0218348X18400042 URL [Cited within: 1]
Effect of pore throat structure on micro-scale seepage characteristics of tight gas reservoirs
Lattice Boltzmann method for fluid flows
DOI:10.1146/annurev.fluid.30.1.329 URL [Cited within: 1]
A lattice Boltzmann BGK model for simulation of micro flows
DOI:10.1209/epl/i2003-10307-8 URL [Cited within: 4]
Application of lattice Boltzmann method to simulate microchannel flows
DOI:10.1063/1.1483841 URL [Cited within: 4]
Microscale effect of microvadose in shale reservoirs
There are abundant nanopores in the organic matter of shales. Gas flow in nano-pores leads to micro-scale effect that can't be described by flowing law of macro fluid. The Lattice Boltzmann Method was applied to simulate gas flow in the nano-channels of organic matter and the effect of slippage, diffusion and adsorption/desorption were considered. The simulation result shows that the compressibility effect of gas leads to the nonlinear pressure distribution along the channels, and the larger the pressure difference, the more serious the nonlinear distribution. To some extent, the enhancement of rarefaction effect weakens nonlinear degree caused by the compressibility effect. With increasing Knudsen number and the pressure differential on the two ends, the slip velocity on the boundary increases, and the velocity vertical to the channel is not zero, increasing the exchange of kinetic energy between gas molecules in channels and molecules at boundary. Slippage effect and adsorption/desorption effect have a significant contribution to the gas mass flow in nano-channels of organic matter.
Numerical modeling of slippage and adsorption effects on gas transport in shale formations using the lattice Boltzmann method
A research method for coal and rock permeability based on lattice Boltzmann method
In order to get the permeability rapidly and exactly under different stress state, a method that combined lattice Boltzmann with uniaxial compression test is proposed to study the rock and coal permeability. Firstly, a destructive compression test was made on the coal-rock, and the stress-strain curve is obtained. And the coal-rock crack images under different stress levels are recorded during the process of compression. Then a simulation program of pore scale lattice Boltzmann is written and verified by Grenoble test. This program can read the crack images and simulate the flow of fluid in the crack, obtain the fluidity pressure and flow velocity. The value of permeability of different crack images can be calculated on the basis of Darcy equation. As a result, the relation curve of the stress-strain and coal-rock permeability is obtained. Through data fitting, we get the strain - permeability relationship, which is compared with the strain - permeability relationship in the literature.
Micro-scale effect in tight gas reservoir based on lattice Boltzmann method. Fault-Block Oil &
Investigation on permeability of shale matrix using the lattice Boltzmann method
Numerical simulation of shale gas flow based on the lattice Boltzmann method at REV scale
Simulation of microscopic gas flowing in shale based on LBM
Pore-scale lattice Boltzmann simulation of micro-gaseous flow considering surface diffusion effect
DOI:10.1016/j.coal.2016.11.013 URL
Analysis on slippage effect in shale gas reservoir based on lattice Boltzmann method
REV-scale simulation of gas transport in shale matrix with lattice Boltzmann method
DOI:10.1016/j.jngse.2018.07.008 URL
Pore scale characteristics of gas flow in shale matrix determined by the regularized lattice Boltzmann method
DOI:10.1016/j.ces.2018.03.056 URL
Pore-scale lattice Boltzmann simulation of two-component shale gas flow
DOI:10.1016/j.jngse.2018.11.011 URL [Cited within: 1]
The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: A review
DOI:10.1016/j.ijheatmasstransfer.2015.12.009 URL [Cited within: 1]
Lattice-Boltzmann simulations of fluid flows in MEMS
DOI:10.1023/A:1014523007427 URL [Cited within: 4]
Rarefaction and compressibility effects of the lattice-Boltzmann-equation method in a gas microchannel. Physical Review E: Statistical, Nonlinear,
Physical symmetry, spatial accuracy, and relaxation time of the lattice Boltzmann equation for microgas flows
DOI:10.1063/1.2185839 URL [Cited within: 8]
Lattice Boltzmann method for gaseous microflows using kinetic theory boundary conditions
DOI:10.1063/1.1897010 URL [Cited within: 4]
Lattice Boltzmann simulation of rarefied gas flows in microchannels. Physical Review E: Statistical, Nonlinear,
Discrete effects on boundary conditions for the lattice Boltzmann equation in simulating microscale gas flows. Physical Review E: Statistical, Nonlinear,
Lattice Boltzmann simulation of dense gas flows in microchannels. Physical Review E: Statistical, Nonlinear,
The mean free path of gas molecules in the transition regime
DOI:10.1088/0022-3727/3/5/307 URL [Cited within: 2]
Lattice Boltzmann modeling of microchannel flows in the transition flow regime
DOI:10.1007/s10404-010-0693-1
URL
[Cited within: 10]

Owing to its kinetic nature and distinctive computational features, the lattice Boltzmann method for simulating rarefied gas flows has attracted significant research interest in recent years. In this article, a lattice Boltzmann (LB) model is presented to study microchannel flows in the transition flow regime, which have gained much attention because of fundamental scientific issues and technological applications in various micro-electro-mechanical system (MEMS) devices. In the model, a Bosanquet-type effective viscosity is used to account for the rarefaction effect on gas viscosity. To match the introduced effective viscosity and to gain an accurate simulation, a modified second-order slip boundary condition with a new set of slip coefficients is proposed. Numerical investigations demonstrate that the results, including the velocity profile, the non-linear pressure distribution along the channel, and the mass flow rate, are in good agreement with the solution of the linearized Boltzmann equation, the direct simulation Monte Carlo (DSMC) results, and the experimental results over a broad range of Knudsen numbers. It is shown that taking the rarefaction effect on gas viscosity into consideration and employing an appropriate slip boundary condition can lead to a significant improvement in the modeling of rarefied gas flows with moderate Knudsen numbers in the transition flow regime.
Rarefaction effects on gas viscosity in the Knudsen transition regime
DOI:10.1007/s10404-010-0606-3 URL [Cited within: 3]
Capturing Knudsen layer phenomena using a lattice Boltzmann model
DOI:10.1103/PhysRevE.74.046704 URL [Cited within: 5]
Lattice Boltzmann modelling Knudsen layer effect in non-equilibrium flows
An extended Navier-Stokes formulation for gas flows in the Knudsen layer near a wall
DOI:10.1209/0295-5075/80/24001 URL [Cited within: 3]
Lattice BGK models for Navier-Stokes equation
DOI:10.1209/0295-5075/17/6/001 URL [Cited within: 1]
A model for collision processes in gases. I. Small amplitude processes in charged and neutral one: Component systems
DOI:10.1103/PhysRev.94.511 URL [Cited within: 1]
Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation
DOI:10.1103/PhysRevE.56.6811 URL [Cited within: 1]
Lattice Boltzmann simulation of immiscible displacement
On pressure and velocity boundary conditions for the lattice Boltzmann BGK model
DOI:10.1063/1.869307 URL [Cited within: 1]
Non-equilibrium extrapolation method for velocity and boundary conditions in the lattice Boltzmann method
DOI:10.1088/1009-1963/11/4/310 URL [Cited within: 1]
Lattice Boltzmann method for simulating gas flow in microchannels
DOI:10.1142/S0129183104005747 URL [Cited within: 1]
Generalized second-order slip boundary condition for nonequilibrium gas flows
DOI:10.1103/PhysRevE.89.013021 URL [Cited within: 2]
Numerical analysis of the shear and thermal creep flows of a rarefied gas over a plane wall on the basis of the linearized Boltzmann equation for hard‐sphere molecules
DOI:10.1063/1.857304 URL [Cited within: 2]
Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow
DOI:10.1103/PhysRevE.77.036707 URL [Cited within: 4]
Gaseous slip flow in long microchannels
DOI:10.1109/84.585795 URL [Cited within: 2]
Examination of the LBM in simulation of microchannel flow in transitional regime
DOI:10.1080/10893950490516983 URL [Cited within: 1]