Introduction
Coal seams are both source rocks and reservoirs of coalbed methane (CBM). Unlike conventional natural gas, CBM is mainly stored in an ads orbed state in pores of the coal reservoir matrix. Coal reservoirs in China have generally low permeability, (0.3-0.5) × 10-3 μm2 on average, and low porosity and pressure besides[1]. For most coalbed methane wells, without stimulation measures, many wells don’t even have industrial development value[2]. Hydraulic fracturing is one of the major CBM recovery techniques. Through hydraulic fracturing, the free and absorbed gases in coal reservoirs would enter the well along fractures to achieve large-scale mining[3,4]. The study of crack initiation and damage mechanisms of CBM reservoirs can guide the design and construction of hydraulic fracturing, and improve the productivity of individual wells[5].
The crack initiation strength and damage strength are important parameters in the reservoir failure process[6]. The crack initiation strength of the coal reservoir refers to the critical strength at which cracks begin to sprout in the reservoir. And the damage strength indicates the strength of coal reservoir when a large number of cracks are interconnected, and is the starting point for the unsteady expansion of cracking. It can be seen that crack initiation strength and damage strength have important guiding significance for the parameter design of reservoir hydraulic fracturing. They are affected by many factors. The effects of a variety of factors on crack initiation and crack propagation of coal reservoirs, such as water saturation[7,8], carbon dioxide saturation[9,10], liquid nitrogen cooling[11], temperature[12], and confining pressure[13], have been studied experimentally. Yang et al.[14] and Feng et al.[15] studied the evolution of acoustic emission events during crack initiation in, and damage to, coal reservoirs with a uniaxial compression test system. Jiang et al.[16] studied the influence of the direction of maximum horizontal principal stress on the form of propagation of hydraulic fractures in coal seams with large inclination by physical simulation experiments. Zhang et al.[17] analyzed the influences of geological factors such as in-situ stress conditions, coal structure, and roof and floor lithology on hydraulic fracturing effect of coal reservoir. Fan et al.[18] studied the influences of fracturing fluid and fracturing technology on hydraulic fractures in coal seam.
The structural characteristics of coal reservoir are also an important factor affecting the hydraulic fracturing effect. Coal reservoirs are typical heterogeneous porous media, with many bedding planes, pores, cleats, and other structurally weak surfaces. The bedding is the first weak joint surface of the coal reservoir, and the cleat is the two sets of natural open fracture systems that are mutually perpendicular and perpendicular to the bedding planes in the coal reservoir. The one that extends longer is face cleat, while the one that is perpendicular and ends at the face cleat is the butt cleat. According to previous studies, the unique fracture system of coal reservoir has important effects on the mechanical properties and permeability of coal reservoir[19,20], and the anisotropy evaluation of coal reservoir is particularly important[21]. Ranjith et al.[22] studied the effects of cleat density and direction on the strength of coal reservoir. Zhang et al.[23], Kossovich et al.[24], Zhao et al.[25], and Liu et al.[26] conducted experimental studies on coal reservoirs with different bedding angles, and found that the coal reservoir exhibits strong anisotropy in uniaxial compressive strength, elastic modulus, dynamic indirect tensile strength, and acoustic emission characteristics. Hao et al.[27] studied the influences of bedding and cleats on the strength of coal reservoir and found that the strength of coal reservoir is mainly affected by bedding, but the effect of cleats cannot be ignored. The current researches on the effects of bedding and cleats on the mechanical properties of coal reservoir mainly focus on uniaxial compressive strength, tensile strength, elastic modulus, and so on. There is hardly any research on the effect of bedding and cleats on the crack initiation strength and damage strength.
The hydraulic fracturing technology for CBM development mainly draws on the hydraulic fracturing technology of conventional petroleum reservoirs[28], but the mechanical properties of coal reservoirs are quite different from those of conventional petroleum reservoirs[4]. Compared with other reservoirs, coal reservoirs not only have lower strength and elastic modulus, a longer non-linear compaction stage, but also have many weak structural surfaces such as bedding and cleats, and feature significant anisotropy in mechanical properties. Because of these differences, coal reservoirs have hydraulic fracturing mechanisms different from conventional petroleum reservoirs, and more complex mechanisms of crack initiation and damage[29]. This makes the current theoretical calculation results of hydraulic fracture initiation of coal reservoirs deviate considerably from the real situation and unable to predict and design the crack initiation strength of hydraulic fracture in coal reservoirs.
In this work, the anisotropy of crack initiation strength and damage strength of coal reservoirs is studied, which is helpful for us to understand the crack initiation strength and damage strength of coal reservoirs with different bedding and cleat angles. The research results provide guidance for the prediction and design of hydraulic fracture initiation pressure, help us understand the occurrence and development direction of hydraulic fractures in coal reservoirs with different bedding and cleat directions, and provide guidance for the optimization of full-scale hydraulic fracturing.
1. Experiment
1.1. Coal seam
The coal reservoir samples used in this work were taken from the 14# coal seam in the Xinzhouyao mine of Datong city. The Xinzhouyao mine has high CBM content, with a CBM emission of 32.55 m3/t. The 14# coal seam belongs to the Jurassic Datong Formation, with a buried depth of 350 m, a coal thickness of 0 to 4.62 m, and an average coal thickness of 1.44 m. The coal belongs to bituminous coal. The 14# coal consists of bright coal and dark coal, with a hard texture, high fracture flatness, and a Protodyakonov coefficient of 3.0 to 4.5.
With widely distributed endogenous fissures, the matrix of the 14# coal seam has significant bedding and cleat structures. To further understand the bedding characteristic of the coal reservoir, the ultrahigh-resolution field emission scanning electron microscope (HIACHISU8010) of China University of Petroleum (Beijing) was used to scan the coal samples, the scanning results are shown in Fig. 1. It can be seen that compared with other reservoirs, the coal reservoir has a large number of weak structural planes such as cleats, and cracks developed inside, and is badly fractured. The beddings are uniform and parallel, and about 80 μm from each other. The break direction of the bedding is basically perpendicular to the direction of the bedding distribution. The direction of cleat is basically perpendicular to the direction of bedding. The cracks in the coal sample are irregularly distributed: most are parallel to the bedding planes, while a small number are at angles with the bedding. The cracks vary in size, and can be up to 100 μm or only a few microns long. From the microscopic point of view, the existence of these bedding planes, cleats, and cracks inside the coal reservoir is bound to lead to anisotropy in the macroscopic mechanical properties of the coal reservoir.
Fig. 1.
Fig. 1.
SEM scanning results of bedding and cleat characteristics of coal reservoir samples.
1.2. Experimental scheme
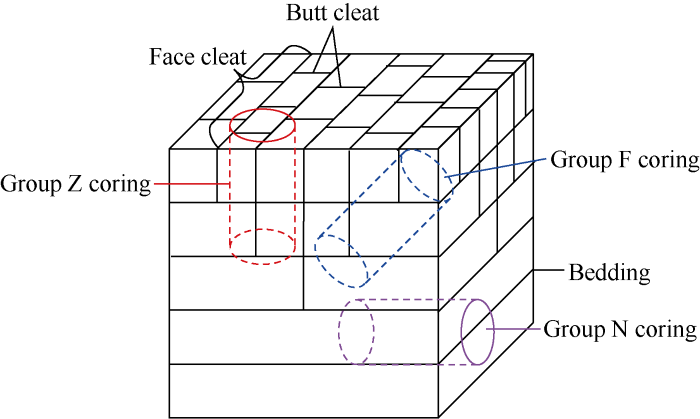
To reduce the discreteness of the samples, the coal reservoir samples were all taken from the same location in the 14# coal seam. According to the method and specification for rock mechanics samples recommended by the International Society of Rock Mechanics, the coal reservoir was sampled as shown in Fig. 2. When drilling samples with different bedding angles, the side parallel to the bedding was fixed to ensure that the direction of the bit and the bedding direction were at an angle, and finally the samples were processed into φ 25 mm × 50 mm standard ones with different bedding angles. After drilling, the fracture network system angles of the three sets of coal reservoir samples are: when the bedding was at any inclination and the inclination angle of 0°, the face cleat was 0° in inclination and 90° in inclination angle, and the butt cleat was 90° in inclination and inclination angle; when the bedding was 0° in inclination and 45° in inclination angle, the face cleat was 180° in inclination and 45° in inclination angle, and the butt cleat was 90° in inclination and 90° in inclination angle; when the bedding was 0° in inclination and 90° in inclination angle, the face cleat was at any angle in inclination and 0° in inclination angle, and the butt cleat was 90° in inclination and 90° in inclination angle. Fig. 2 shows that the beddings, face cleats, and butt cleats are perpendicular with each other. When the bedding angle is determined, the angles of face cleat and butt cleat are determined, therefore, only the bedding angle (0°, 45°, 90°) is used to describe the fracture network system of the coal reservoir. Six samples at each bedding angle were prepared, making a total of 18 samples. Among them, the coal reservoir samples with a bedding angle of 0° (horizontal bedding) are recorded as Z group; the coal reservoir samples with a bedding angle of 45° are recorded as F group; the coal reservoir samples with a bedding angle of 90° (vertical bedding) are recorded as N group. Each sample was cut and polished after drilling to ensure that the parallel deviation between the two ends of the sample was no more than 0.05 mm, the size deviation of two ends was no more than 0.2 mm, the end surface was perpendicular to the sample axis, and the maximum angular deviation didn’t exceed 0.25°.
Fig. 2.
Fig. 2.
Schematic diagram of the internal structure and sample coring of coal reservoir.
To compare the discreteness of coal reservoir samples, the axial longitudinal wave velocities of the 18 samples were tested. The test results are shown in Table 1. It can be seen from the table that the wave velocities of samples are mainly affected by the bedding angle. Because the wave velocities of samples F5 and N5 differ widely from the wave velocities of other samples at the same bedding angle, samples F5 and N5 were eliminated.
Table 1 Test results of axial longitudinal wave velocities of coal reservoir samples.
| Bedding angle/(°) | Sample No. | Wave velocity/(km·s-1) |
|---|---|---|
| 0 | Z1 | 1.15 |
| Z2 | 1.14 | |
| Z3 | 1.13 | |
| Z4 | 1.16 | |
| Z5 | 1.13 | |
| Z6 | 1.09 | |
| 45 | F1 | 1.18 |
| F2 | 1.20 | |
| F3 | 1.19 | |
| F4 | 1.17 | |
| F5 | 1.07 | |
| F6 | 1.18 | |
| 90 | N1 | 1.17 |
| N2 | 1.18 | |
| N3 | 1.21 | |
| N4 | 1.25 | |
| N5 | 1.10 | |
| N6 | 1.26 |
1.3. Experimental equipment
The coal reservoir samples were loaded in an MTS815.04 rock mechanics testing machine at Wuhan Institute of Coal and Rock Mechanics, Chinese Academy of Sciences, and uniaxial compression testing was conducted under strain control. The loading rate was 5.0 × 10-6 mm/s. The DISP acoustic emission signal acquisition system produced by PAC Company was used to study the evolution of acoustic emission events of coal under uniaxial loading. In the process of the experiment, the loading and the monitoring of acoustic emission were carried out simultaneously.
2. Results and discussion
2.1. Results of crack initiation strength and damage strength
The methods used to determine the crack initiation strength and damage strength of coal reservoir include crack volume strain method, acoustic emission parameter value method, lateral strain and volume strain curve observation method, and moving point regression method. Crack volume strain method is the most commonly used at present. Therefore, crack volume strain method was used to determine uniaxial crack initiation strength and damage strength of coal reservoirs in this study.
By subtracting the elastic volume strain from the volume strain, the crack volume strain reflecting crack closure and opening during loading can be obtained. The elastic volume strain and crack volume strain are calculated by the following formulas:
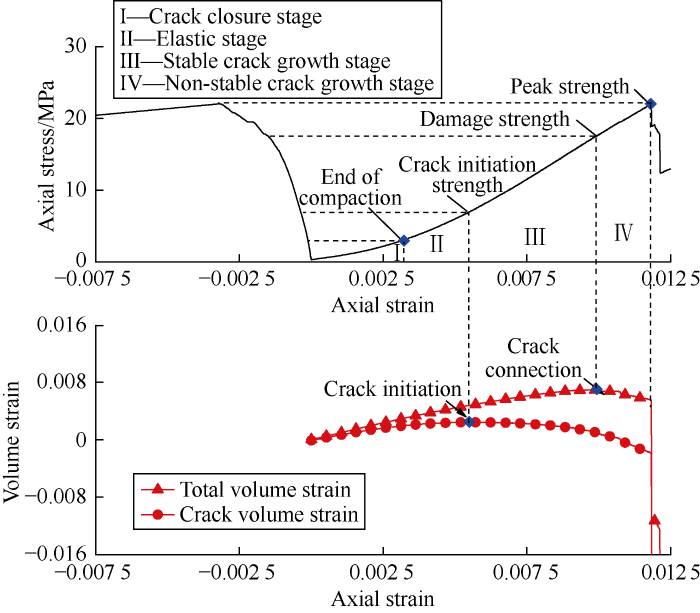
The typical crack volume strain curve of the coal reservoir sample under uniaxial compression is shown in Fig. 3. The coal reservoir sample is the F1 sample with a bedding angle of 45°. In crack closure stage (Stage I), the crack volume strain is positive and the slope of the curve is positive, which indicate that the volume of the coal reservoir sample is decreasing; in the elastic stage (Stage II), theoretically, the increment of coal volume strain is equal to the increment of elastic volume strain, but there is a little difference between the two because coal has a non-linear elastic stage; in stable crack growth stage (Stage III) and non-stable crack growth stage (Stage IV), the total volume strain includes the volume increase caused by crack opening, leading to a negative slope of the crack volume strain curve. Therefore, the stress corresponding to the inflection point where the slope of the crack volume strain curve is zero is the crack initiation strength; the stress corresponding to the point where the slope of the total volumetric strain curve is zero is the damage strength. Accordingly, the F1 sample is determined to have a crack initiation strength of 6.9 MPa and damage strength of 17.5 MPa.
Fig. 3.
Fig. 3.
Crack volume strain diagram of coal reservoir sample F1.
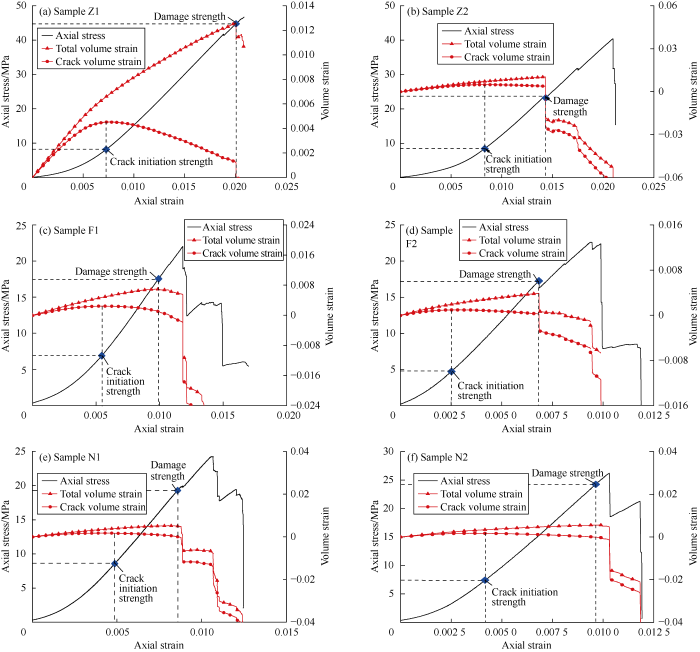
Fig. 4 shows the examples of crack volume strain curves of coal reservoir samples with different bedding angles. Due to sensor failure, the parameters of sample N6 were not obtained. According to the above method, it can be concluded that the samples have crack initiation strength between 4.7 and 10.4 MPa and damage strength between 7.8 and 47.6 MPa. It can be seen that the strength of coal reservoirs shows significant anisotropy due to the influence of fracture network systems such as bedding and cleats in them. The index used to measure the anisotropy of rock strength is the degree of anisotropy[33]:
Fig. 4.
Fig. 4.
Typical crack volume strain curves of coal reservoir samples with different bedding angles.
Through calculation, the degree of anisotropy of uniaxial compressive strength of the coal reservoir is 1.94. Similarly, the degree of anisotropy of crack initiation strength is 1.49 and the degree of anisotropy of damage strength is 2.31.
2.2. Anisotropy of crack initiation and damage strengths
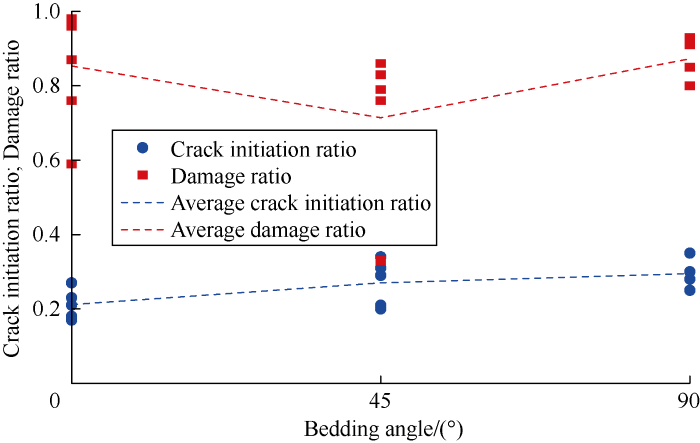
To analyze the anisotropy of crack initiation strength and damage strength, the variations of crack initiation strength, damage strength, compressive strength, crack initiation ratio (the ratio of the crack initiation strength to the compressive strength), and damage ratio (the ratio of the damage strength to the compressive strength) with bedding angle were studied (Figs. 5 and 6).
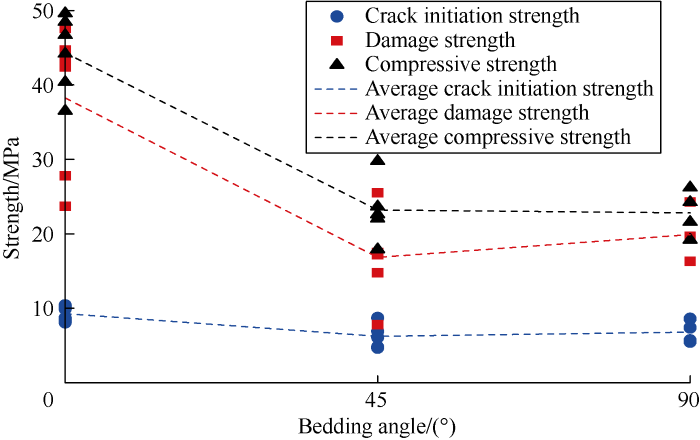
It can be seen from Fig. 5 that the crack initiation strength first decreases and then increases with the increase of bedding angle. When the bedding angle is 0°, the average value of the crack initiation strength is the largest (9.28 MPa); when the bedding angle is 45°, the average value of the crack initiation strength significantly reduces (6.24 MPa); when the bedding angle is 90°, the crack initiation stress is not much different from that at the bedding angle of 45°, with an average of 6.80 MPa. The damage strength also shows the similar variation trend. The compressive strength decreases with the increase of the bedding angle, but the compressive strength at the bedding angle of 45° is not much different from that at the bedding angle of 90°.
Fig. 5.
Fig. 5.
The variations of crack initiation strength, damage strength and compressive strength with bedding angle.
It can be seen from Fig. 6 that the crack initiation ratio values range from 0.17 to 0.35, with an average of 0.25. With the increase of the bedding angle, the crack initiation ratio increases in general. The damage ratio values range in a large span from 0.33 to 0.98, with an average of 0.81. With the increase of the bedding angle, the damage ratio decreases first and then increases. At the bedding angle of 45°, the damage ratio is the smallest.
Fig. 6.
Fig. 6.
The variation trends of crack initiation ratio and damage ratio with bedding angle.
3. Anisotropy of acoustic emission (AE) in coal reservoirs
3.1. Acoustic emission characteristics of coal reservoir under uniaxial compression
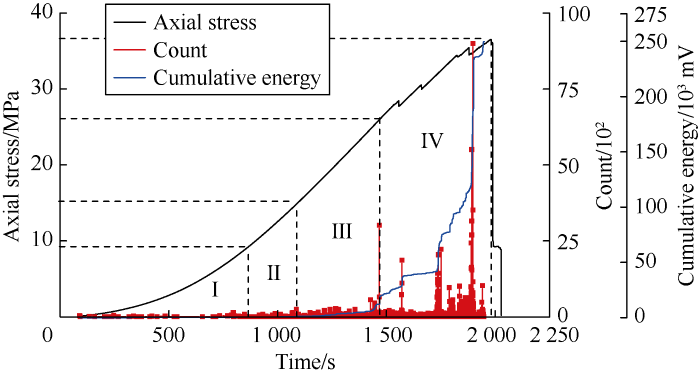
The variation of acoustic emission event count and cumulative energy with time during the uniaxial compression of a typical coal reservoir sample Z5 with a bedding angle of 0° is shown in Fig. 7. In the crack closure stage (Stage I), some AE events occurred, indicating that some crystals in the CBM reservoir had friction and
extrusion when the cracks closed, producing a small number of low energy AE events. In the elastic stage (stage II), the AE events of the CBM reservoir sample were more than that in stage I, but still low in energy. In the stage of stable crack growth (Stage III), the AE counts and cumulative energy began to rise gradually, indicating that microcracks began to appear inside the CBM reservoir sample in this stage. In the stage of instable crack growth (Stage IV), the AE count and cumulative energy increased significantly, indicating that the cracks in the CBM reservoir sample rapidly expanded and connected with each other. When the stress approached the compressive strength, the AE events were very active. With the penetration of the macroscopic cracks, the AE count reached the maximum at the peak compressive strength.
Fig. 7.
Fig. 7.
Variations of acoustic emission cumulative energy, count and axial stress of sample Z5 with time under uniaxial compression.
3.2. The bedding effect of acoustic emission count and energy
The variation trends of cumulative count and cumulative energy of acoustic emission with the bedding angle are shown in Fig. 8. It can be seen that the AE characteristics also have recognizable bedding effect. The cumulative count of the samples with a bedding angle of 45° is slightly larger than the samples with a bedding angle of 0°. The samples with a bedding angle of 90° have the least cumulative count. The results indicate that the samples with a bedding angle of 45° had the most frequent AE activities during the uniaxial compression process, followed by the samples with a bedding angle of 0°, and the samples with a bedding angle of 90° had the fewest. This indicates that the samples with the bedding angle of 45° had the most frequent crack generation and propagation under the same stress conditions. But from the cumulative energy, the coal reservoir samples with a bedding angle of 0° had the largest cumulative energy released on average. These results may be attributed to the fact that AE events occurred throughout the whole compression process of the samples with the bedding angle of 0°, resulting in a relatively large number of AE counts. The failure is mainly caused by the fracture of the matrix in the coal reservoir, so these samples had the largest cumulative energy released. But for the coal samples with the bedding angle of 45°, the slip failure occurred along the bedding plane during the loading process, so there was more friction between bedding planes, and the cumulative count was the largest. However, slip failure between the bedding planes took dominance, and so the cumulative energy released was smaller. For the samples with the bedding angle of 90°, the bedding direction was consistent with the loading direction. When the stress was low, the bedding planes were not squeezed, so the count and energy were less. When the stress was high, microcracks began to occur in the samples, so the cumulative count and cumulative energy began to increase. The failure is mainly induced by tensional failure between bedding planes with less energy released, so the cumulative count and cumulative energy were both small.
Fig. 8.
Fig. 8.
The relationships between cumulative count and cumulative energy of acoustic emission events and bedding angle.
3.3. The bedding effect of crack initiation strength and damage strength based on AE count
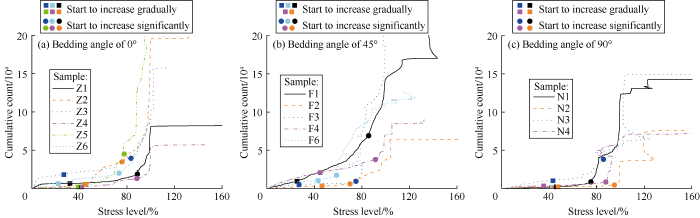
The variation curves of AE cumulative count with stress level (ratio of axial stress to compressive strength) of the samples are shown in Fig. 9. The part of the abscissa where the stress level that exceeds 100% represents the stress level after reaching the peak strength, for example, 120% on the abscissa represents the stress level of 80% after reaching the peak strength. It can be seen from Fig. 9 that the samples with different bedding angles had different stress levels corresponding to the gradual and significant increases of the cumulative count of AE. During the uniaxial compression of coal reservoir samples, AE signals are generated when the cracks initiate and grow. The gradual increase of AE activities indicates that microcracks began to turn up inside the coal reservoir sample. The stress at this point is the crack initiation strength. The significant increase of AE activity marks the rapid propagation and connection of cracks in the coal reservoir sample. The stress at this point is the damage strength. For the samples with the bedding angle of 0°, the stress level at which the cumulative count of the AE starts to gradually grow is between 22% and 45%, mostly below 40%, and on average 34.47%. The stress level at which the cumulative energy of AE starts to grow significantly is between 73% and 88%, on average 81.18%. For the samples with the bedding angle of 45°, the stress level at which the cumulative count of the AE starts to gradually grow is between 25% and 46%, on average 37.38%. The stress levels at which the cumulative count of the AE starts to significantly grow are more discrete, with the minimum of 59%, the maximum of 91%, and an average of 76.17%. For the samples with the bedding angle of 90°, the stress level at which the cumulative count of the AE starts to gradually grow is between 35% and 48%, on average 43.04%. The stress level at which the cumulative count of the AE starts to grow significantly is between 75% and 95%, on average 85.85%. These results show that the crack initiation ratio of coal reservoirs determined by the cumulative count of the AE increases with the increase of bedding angle, while the damage ratio determined by the cumulative count decreases firstly and then increases with the increase of bedding angle, and is the smallest at the bedding angle of 45°. This is consistent with the previous conclusion obtained by the crack volume strain method.
Fig. 9.
Fig. 9.
The variations of AE cumulative count with stress level of coal reservoir samples with different bedding angles.
3.4. The bedding effect of crack initiation strength and damage strength based on AE energy
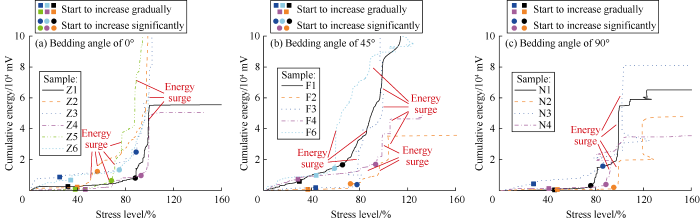
Fig. 10 shows the curves of AE cumulative energy with stress of the samples. It can be seen that the samples with different bedding angles differ in stress levels corresponding to the gradual and significant growth of the cumulative energy of AE too. For the samples with the bedding angle of 0°, the average stress levels at which the cumulative energy starts to grow gradually and then significantly are 36.01% and 78.28%, respectively. For the samples with the bedding angle of 45°, the average stress levels at which the cumulative energy starts to grow gradually and then significantly are 36.48% and 73.63%, respectively. For the samples with the bedding angle of 90°, the average stress levels at which the cumulative energy starts to grow gradually and then significantly are 41.11% and 86.71%, respectively. These results show that the crack initiation ratio of coal reservoir (as determined by the cumulative energy of AE) increases with increase of bedding angle. The damage ratio determined by cumulative energy first decreases, then increases with the increase of bedding angle and is the smallest at the bedding angle of 45°. This is consistent with the conclusion based on the acoustic emission count.
Fig. 10.
Fig. 10.
The variation curves of AE cumulative energy with stress level of coal reservoir samples with different bedding angles.
It can also be seen from Fig. 10 that some samples with the bedding angles of 0° and 45° had several energy surges before the peak compressive strength. This may be because the direction of bedding is inconsistent with the loading direction, so the bedding inhibits the growth of vertical cracks, and it is difficult for the cracks to penetrate the samples at once. In contrast, the samples with a bedding angle of 90° had only one energy surge before the peak compressive strength. This is because the direction of the bedding of these samples is parallel to the loading direction, and the bedding cannot inhibit the growth of the vertical cracks, so the vertical cracks rapidly penetrate the samples and release most energy.
3.5. Anisotropic of acoustic emission amplitude
The amplitude of an AE event can be used to describe the intensity of the AE event. Analysis of the amplitude distribution of the AE events during the axial compression process of the coal reservoir samples can give up a better understanding on the process of crack initiation and damage in the CBM reservoirs.
The amplitude distribution of the AE events can be described by the parameter b. Parameter b was originally used in the field of earthquake. Gutenberg and Richter proposed the Gutenberg-Richter (G-R) relation in 1941[34]:
At present, research on the parameter b is not limited to the field of earthquakes. There are many calculation methods for the value of b, such as the least square and maximum likelihood estimation methods[35]. In this study, the maximum likelihood estimation method was used to calculate the value of b:
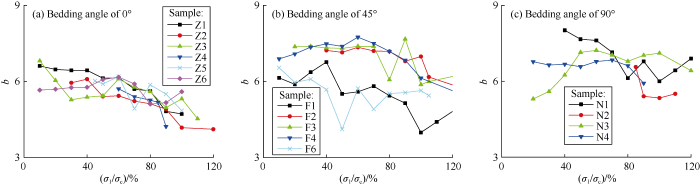
The b-value during the uniaxial compression of each sample was calculated by Eq. (6), and the calculation results are shown in Fig. 11. The dynamic characteristics of the b-value have specific physical meaning. The increase of b-value means the proportion of small-scale events increases, and the cracking is dominated by small-scale fractures. The b-value keeping constant indicates that the large- and small-scale AE events are relatively stable in proportion. The decrease of b-value means that the proportion of large-scale events increases, and the cracking is dominated by large-scale fractures. Fluctuation of the b-value in a small range indicates that the cracks propagate slowly and steadily. Sudden leap of b-value a large range means a sudden change of failure process and represents suddenly instable propagation.
Fig. 11.
Fig. 11.
Dynamic characteristics of b-values of coal reservoir samples with different bedding angles.
It can be seen from Fig. 11 the dynamic variations of the b-values of the coal reservoir samples with different bedding angles have some common characteristics. The samples have higher b-values before reaching the peak compressive strength, which indicates that when the stress level is relatively low, the cracks turning up are largely small ones. When the stress level increases, the value of b decreases, which indicates that the large number of small-scale fractures connect with each other and go through the coal sample, and the cracking is dominated by large-scale fractures at this point. The dynamic changes of b values of the coal reservoir samples with different bedding angles also show some different characteristics. The samples with a bedding angle of 0° have steady decrease of b variation magnitude with the increase of stress level, indicating that the failure of the samples with a bedding angle of 0° is mainly steady propagation of large-scale fractures. Out of the samples with the bedding angle of 45°, some (F2, F4) have drop of b-values when the stress is higher, suggesting that these samples have stable micro-cracks in the initial stage of loading, then when the stress level is high, cracks connect with each other and go through the samples, resulting in instable propagation, which is a process of steady propagation of fractures. The b-values of the remaining samples (F1, F3, F6) fluctuate in a large range in all the stages of uniaxial compression, indicating that these samples have unstable proportions of large- and small-scale fractures at all stages, and the failure of this type of sample is due to sudden-instability of fractures. The samples with the bedding angle of 90° have b-values fluctuating in a large range. For these samples, the fractures at different scales are relatively stable in the initial stage of loading, but when the stress reaches peak, the cracks rapidly propagate along the bedding plane. The cracks in this type of sample propagate quite violently, resulting in sudden failure of the samples.
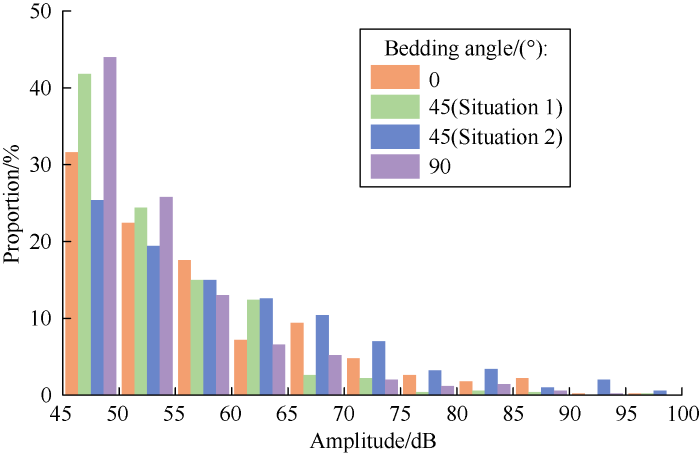
Fig. 12 shows the proportions of AE events of different amplitude segments of the samples with different bedding angles at peak strength. It can be seen that the coal reservoir samples with a bedding angle of 90° have much less large amplitude AE events than the samples with a bedding angle of 0°. The samples with a bedding angle of 45° show two different situations, some have more small- amplitude events, while the others have more large-amplitude events.
Fig. 12.
Fig. 12.
Proportions of AE events in different amplitude segments of the samples with different bedding angles at peak stress.
Based on the above analysis, the coal reservoir samples with the bedding angle of 90° have sudden failure and a lower proportion of large-scale fractures. In comparison, the coal reservoir samples with the bedding angle of 0° have failure caused by steady propagation of fractures and higher proportion of large-scale fractures. The coal reservoir samples with the bedding angle of 45° have two types of failure, one type features the steady propagation of fractures and larger proportion of small-scale fractures; the other type features sudden instability and larger proportion of large-scale fractures. This is because the bedding angle of these samples is in a certain angle with the loading direction, both some small-scale fractures between the bedding and some large-scale cracks along the bedding planes may turn up.
4. Discussion
4.1. The applicability of identifying the crack initiation strength and damage strength of coal reservoirs based on acoustic emission
Hydraulic fracturing is an important technique that can increase permeability and production during the development of CBM. Micro-seismic monitoring technology and AE are often used to monitor cracking initiation and propagation in deep strata. It can be seen from the previous results that the AE activities in the coal samples show different characteristics when the cracks initiate and propagate in the samples. AE can also be used to determine the crack initiation strength and damage strength of the coal reservoir. However, the applicability of AE count and AE energy in assessing the crack initiation and damage of the coal reservoir with bedding has not been discussed before. Therefore, in this work, the crack initiation strengths and damage strengths calculated by the crack volume strain method and the acoustic emission method were compared and analyzed. It can be seen from Table 2, for most samples, the crack initiation strength and damage strength obtained from the cumulative AE counts are relatively close to that obtained from the cumulative AE energy. This is because during uniaxial compression of the coal reservoir, crack initiation and propagation are accompanied by AE events. As the number of AE events increases, a large amount of energy is usually released. However, the results of some samples are quite different, for example, the sample F4.
Table 2 Crack initiation strengths and damage strengths of coal reservoir samples from different methods.
| Sample No. | Crack initiation strength/MPa | Crack initiation ratio | Damage strength/MPa | Damage ratio | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Crack volume strain method | AE method | Crack volume strain method | AE method | Crack volume strain method | AE method | Crack volume strain method | AE method | |||||
| AE count | AE energy | AE count | AE energy | AE count | AE energy | AE count | AE energy | |||||
| Z1 | 8.1 | 14.96 | 14.96 | 0.17 | 0.320 3 | 0.320 3 | 44.7 | 41.44 | 41.17 | 0.96 | 0.887 3 | 0.881 6 |
| Z2 | 8.4 | 18.14 | 16.07 | 0.21 | 0.449 0 | 0.397 8 | 23.7 | 30.61 | 22.84 | 0.59 | 0.757 8 | 0.565 5 |
| Z3 | 10.2 | 11.88 | 11.14 | 0.23 | 0.268 8 | 0.252 1 | 42.4 | 36.84 | 39.27 | 0.96 | 0.833 8 | 0.888 8 |
| Z4 | 8.7 | 20.35 | 22.55 | 0.18 | 0.419 8 | 0.465 3 | 47.6 | 42.83 | 45.05 | 0.98 | 0.883 6 | 0.929 5 |
| Z5 | 9.9 | 14.21 | 13.92 | 0.27 | 0.389 0 | 0.381 1 | 27.8 | 28.33 | 24.94 | 0.76 | 0.775 8 | 0.683 0 |
| Z6 | 10.4 | 10.98 | 17.06 | 0.21 | 0.221 3 | 0.343 8 | 43.3 | 36.35 | 37.15 | 0.87 | 0.732 5 | 0.748 6 |
| F1 | 6.9 | 5.59 | 6.54 | 0.31 | 0.253 6 | 0.296 8 | 17.5 | 18.89 | 14.48 | 0.79 | 0.856 9 | 0.656 8 |
| F2 | 4.7 | 10.51 | 8.33 | 0.21 | 0.465 0 | 0.368 3 | 17.2 | 15.83 | 16.36 | 0.76 | 0.700 3 | 0.723 4 |
| F3 | 6.1 | 4.86 | 7.78 | 0.34 | 0.271 2 | 0.434 3 | 14.8 | 13.44 | 13.93 | 0.83 | 0.750 6 | 0.777 7 |
| F4 | 4.8 | 10.60 | 6.78 | 0.20 | 0.448 1 | 0.286 7 | 7.8 | 21.62 | 22.07 | 0.33 | 0.913 7 | 0.933 0 |
| F6 | 8.7 | 12.83 | 13.04 | 0.29 | 0.431 0 | 0.437 9 | 25.5 | 17.47 | 17.58 | 0.86 | 0.586 8 | 0.590 5 |
| N1 | 8.6 | 11.15 | 11.17 | 0.35 | 0.459 7 | 0.460 7 | 19.3 | 18.23 | 18.49 | 0.80 | 0.751 6 | 0.762 6 |
| N2 | 7.4 | 12.46 | 12.70 | 0.28 | 0.475 3 | 0.484 7 | 24.3 | 24.88 | 25.00 | 0.93 | 0.949 1 | 0.953 8 |
| N3 | 5.7 | 7.64 | 8.92 | 0.25 | 0.353 9 | 0.413 0 | 19.7 | 18.92 | 19.19 | 0.91 | 0.876 5 | 0.888 9 |
| N4 | 5.5 | 8.31 | 5.49 | 0.30 | 0.432 8 | 0.286 1 | 16.3 | 16.45 | 16.57 | 0.85 | 0.856 9 | 0.863 1 |
Taking the results of the crack volume strain method as the reference, the results obtained from the cumulative AE count and cumulative energy were compared, as shown in Fig. 13. It can be seen from Fig. 13(a), the average difference between the crack initiation strengths obtained by the cumulative count and crack volume strain method is 55.7%, the average difference between the crack initiation strengths obtained by the cumulative energy and crack volume strain method is 53.1%. It can be seen from Fig. 13(b), the average difference between the crack initiation strengths obtained by the cumulative count and crack volume strain method is 7.8%, the average difference between the crack initiation strengths obtained by the cumulative energy and crack volume strain method is 4.9%. The above results show that the results calculated by the cumulative energy method are closer to those of crack volumetric strain method than the cumulative count method. When the acoustic emission parameters are used to determine the crack initiation and penetration of coal reservoirs, the results obtained by the cumulative energy method are more accurate.
Fig. 13.
Fig. 13.
Comparison of crack initiation strengths and damage strengths from cumulative AE count and cumulative AE energy methods and crack volume strain method.
4.2. The intrinsic mechanism of anisotropy of crack initiation strength and damage strength anisotropy
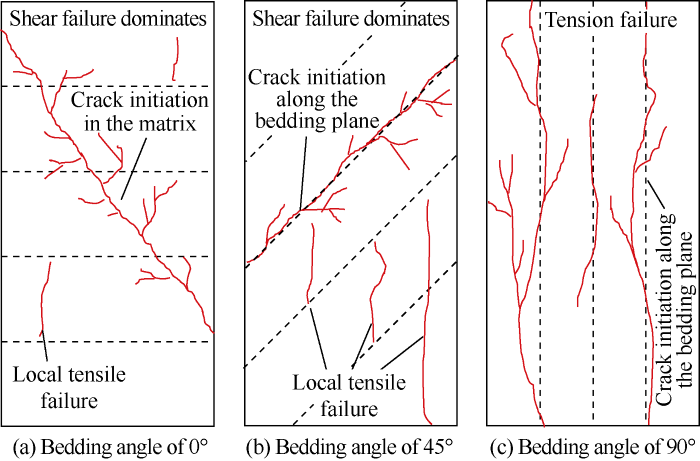
When the bedding angle of the coal reservoir sample is 0°, the bedding plane is perpendicular to the applied stress. According to the Jager failure criterion, the cracks will gradually expand and penetrate the rock matrix, as shown in Fig. 14(a). In this case, the bedding has no effect on the crack propagation and failure of the coal reservoir matrix. Therefore, when the bedding angle is 0°, the crack initiation strength and damage strength are both larger.
Fig. 14.
Fig. 14.
Crack initiation and propagation models of coal reservoir samples with different bedding angles.
When the bedding angle of the coal reservoir sample is 45°, as the bedding plane and the loading direction intersect obliquely, the cracks would initiate and propagate almost along the bedding plane. At the same time, due to the complexity of the fracture system (as exemplified by the bedding and cleats of the coal reservoir), local tensile failure would appear (Fig. 14b). The strength of the coal reservoir is manifested as the strength of the bedding plane, and the strength of the bedding plane is much smaller than the matrix strength of the coal reservoir, which leads to smaller crack initiation strength and damage strength of the coal reservoir with a bedding angle of 45°. When the bedding angle of the coal reservoir sample is 90°, the bedding plane is parallel to the loading direction. Due to the presence of bedding planes, the coal reservoir samples are prone to tensile fracturing due to the lateral strain exceeding its limiting value (Fig. 14c). The cracks of this type of sample gradually turn up along the outer edge and propagate constantly toward the inner coal reservoir. Due to the low tensile strength of the coal reservoir bedding plane, the crack initiation strength and damage strength of coal reservoir with a bedding angle of 90° are also smaller.
Compared with the sample with a bedding angle of 90°, the crack initiation strength and damage strength of the sample with a bedding angle of 45° are lower. This is because, although the failures of samples with bedding angles of 45° and 90° are both closely related to bedding, according to the previous analysis of AE cumulative event count, cumulative energy, and failure mode, it can be seen that, only when the stress is quite high, cracks in the sample with a bedding angle of 90° begin to propagate rapidly, therefore, the crack initiation strength and damage strength of the sample with a bedding angle of 90° are slightly larger than that of the sample with a bedding angle of 45°.
5. Conclusions
The mechanical properties of coal reservoirs show obvious anisotropy. For the coal reservoir samples taken from 14# coal seam in Xinzhouyao of Datong city, the degree of anisotropy of uniaxial compressive strength of the coal reservoir is 1.94, the degree of anisotropy of crack initiation strength is 1.49, and the degree of anisotropy of damage strength is 2.31. The compressive strength decreases with the increase of bedding angle, but the compressive strength of the sample with a bedding angle of 45° is not much different that with a bedding angle of 90°. Both crack initiation strength and damage strength first decrease and then increase with the increase of bedding angle. When the bedding angle is 0°, the crack initiation strength and damage strength are the highest, followed by those at 90°, and those at 45° are the lowest. The crack initiation strength of the sample with a bedding angle of 0° is 1.49 times that of the sample with a bedding angle of 45° and 1.37 times that of the sample with a bedding angle of 90°. The damage strength of the sample with a bedding angle of 0° is 2.31 times that of the sample with a bedding angle of 45° and 1.92 times that of the sample with a bedding angle of 90°.
The coal reservoir samples with the bedding angle of 90° have the smallest cumulative count and cumulative energy of AE events under uniaxial compression, and have only one energy surge before the compressive strength The coal reservoir samples with the bedding angle of 45° have the largest cumulative count of AE events. The coal reservoir samples with the bedding angle of 0° have the largest cumulative energy of AE. The coal reservoir samples with the bedding angles of 0° or 45° have several energy surges before the compressive strength.
The failure of the coal reservoir samples with the bedding angle of 0° is the process of steady fracture propagation dominated by large-scale fractures. The failure of the samples with the bedding angle of 90° is mainly due to sudden instability of fractures, with a lower proportion of large-scale ones. The coal reservoir samples with the bedding angle of 45° have two types of failure, one type is the result of steady propagation of fractures, mainly small-scale ones; the other type of failure is the result of sudden instability of fractures, mainly large-scale ones.
Compared with the cumulative AE event count, the cumulative energy of AE events is more suitable for determining the crack initiation strength and damage strength of coal reservoir.
In addition to bedding and cleats, coal reservoirs may also have natural fractures, which will affect their mechanical properties. The effects of natural fractures on crack initiation strength and damage strength of coal reservoirs will be researched further.
Nomenclature
a, b—constant;
Ai—the amplitude of the i-th acoustic emission event;
Amin—the minimum amplitude of the AE events;
E—elastic modulus obtained from the experimental stress- strain curve of the linear elastic stage of the sample, MPa;
Rc—anisotropy degree, dimensionless;
M—magnitude;
N—the number of earthquakes in the range of M+ΔM;
n—the total number of AE events;
ε1—axial strain, dimensionless;
ε3—circumferential strain, dimensionless;
εv—volume strain, dimensionless;
εvc—crack volume strain, dimensionless;
εve—elastic volume strain, dimensionless;
σ1—axial stress, MPa;
σc—compressive strength, MPa;
σcmax, σcmin—maximum and minimum values of average uniaxial compressive strength of samples at different bedding angles, MPa;
υ—Poisson’s ratio obtained from the experimental stress-strain curve of the linear elastic stage of the sample, dimensionless.
Reference
The classification and model of coalbed methane reservoirs
DOI:10.1111/acgs.2004.78.issue-3 URL [Cited within: 1]
Relationship of the permeability and geological strength index (GSI) of coal reservoir and its significance
Progress and application of hydraulic fracturing technology in unconventional reservoir
Experimental investigation on fracture initiation and non-planar propagation of hydraulic fractures in coal seams
Hydraulic fracturing simulation test and fracture propagation analysis of large-scale coal rock under true triaxial conditions
The effects of crack openings on crack initiation, propagation and coalescence behavior in rock-like materials under uniaxial compression
DOI:10.1007/s00603-016-0998-9 URL [Cited within: 1]
An experimental investigation on behaviour of coal under fluid saturation, using acoustic emission
DOI:10.1016/j.jngse.2014.12.020 URL [Cited within: 1]
Effects of water intrusion on mechanical properties of and crack propagation in coal
Effects of saturation medium and pressure on strength parameters of Latrobe Valley brown coal: Carbon dioxide, water and nitrogen saturations
DOI:10.1016/j.energy.2011.09.026
URL
[Cited within: 1]

Adsorption of carbon dioxide (CO2) into coal matrix causes significant change in its chemical and physical structure, resulting in negligible permeability values and overall strength reduction. The main objective of this study is to investigate the effects of water, nitrogen (N-2) and CO2 saturations at different saturation pressures on the strength of brown coal using uniaxial experiments. A series of uniaxial experiments was conducted on 38 mm diameter by 76 mm height Latrobe Valley brown coal samples with different saturation media (water, N-2, CO2) and pressures (1, 2 and 3 MPa). According to the test results, water and CO2 saturations cause the uniaxial compressive strength (UCS) of brown coal to be reduced by about 17% and 10% respectively. In contrast, N-2 saturation causes it to increase by about 2%. Moreover, Young's modulus of brown coal is reduced by about 8% and 16% due to water and CO2 saturations respectively, and is increased up to 5.5% due to N-2 saturation. It can be concluded that CO2 and water saturations cause the strength of brown coal to be reduced while improving its toughness, and N-2 saturation causes the strength of brown coal to increase while reducing its toughness. The fracture propagation pattern of each sample was then observed using advanced acoustic emission (AE). Findings indicate that CO2 saturation causes early crack initiation due to the CO2 adsorption-induced swelled layer and early crack damage and failure points due to lower surface energy. In contrast, N-2 saturation causes delays in crack initiation, damage and failure due to the removal of both water and naturally available CO2 from the coal mass during the saturation. (C) 2011 Elsevier Ltd.
The effect of CO2 saturation on mechanical properties of Australian black coal using acoustic emission
DOI:10.1016/j.fuel.2010.03.025
URL
[Cited within: 1]

Abstract
Acoustic emission (AE) methods are now widely used for damage evaluation. For a better understanding of the damage mechanics of materials such as rocks, AE has been used to monitor stresses which induce crack closure, crack initiation and crack damage. In the present study, an AE system was used to study the damage behaviour of some Australian black coal samples subjected to uniaxial compression. Several samples were left in a container filled with 100% carbon dioxide (CO2) at a certain pressure for 72 h prior to testing. The results were compared with samples which had only been exposed to the atmosphere to see if CO2 had any adverse effect on the strength of coal. Strain gauges were installed on the samples and the measured axial and volumetric strains were studied in conjunction with the AE counts.
The AE method was successfully used for detecting the onset of crack initiation and the crack damage stress threshold of the black coal samples. Of the coal samples examined, crack initiation and crack closure of the samples subjected to saturation with CO2 occurred at stress corresponding to a higher percentage of the peak strength when compared to the samples which had only been exposed to atmospheric conditions. However, crack damage occurred at a higher percentage of peak strength and the average peak strength showed a higher value for samples in atmospheric condition when compared to CO2 saturated samples. The results show that sorption of CO2 can cause a reduction in strength of the black coal samples when tested under uniaxial compression. As the coal samples were highly inhomogeneous more tests are required in order to be able to confirm whether the adsorption of CO2 will cause strength reduction in coal and to identify the actual underlying mechanisms.
Research of fracturing mechanism of coal subjected to liquid nitrogen cooling
Crack closure and initiation stresses of coal subjected to thermo-gas-mechanical coupling
DOI:10.2298/TSCI17S1301G URL [Cited within: 1]
Estimation of crack initiation and propagation thresholds of confined brittle coal specimens based on energy dissipation theory
DOI:10.1007/s00603-017-1317-9 URL [Cited within: 1]
Study on acoustic emission evolution characteristic of plastic and brittle coal failure process
Strength restoration of cracked sandstone and coal under a uniaxial compression test and correlated damage source location based on acoustic emissions
Experimental investigation on hydraulic fracture geometry in high-dip coal seam
Influence of geological factors on hydraulic fracturing effect of coalbed methane wells in Shizhuangnan block, Qinshui Basin
Influence of injection rate and fracturing fluid viscosity on hydraulic fracture geometry in coal
Coal cleat system characteristics and formation mechanisms in the Qinshui Basin
As the source rock and reservoir of coalbed methane (CBM), coal bed is different from conventional gas reservoirs in its dual porosity rock composed of matrix pore and fracture and being of its unique cleat system. The size, shape, porosity and connectivity of matrix pore and cleat determine accumulation, migration and production of CBM, with cleat system being most important for CBM production. Taken the Qinshui coal field as an example, this paper focuses on the type of coal cleats and fillings, fillings way, and formation age of authigenic minerals of coal cleat. Based on formation age of filling and burial history of coal bed, three formation mechanisms of cleat were proposed: buried pressurization mechanism; magma induced mechanism; uplift depressurized mechanism.
Progress of the research on coal-bed gas reservoir permeability
Anisotropy interpretation and the coherence research between resistivity and acoustic anisotropy in tight sands
Effects of cleat performance on strength reduction of coal in CO2 sequestration
DOI:10.1016/j.energy.2012.05.041
URL
[Cited within: 1]

The natural cleat system in coal is highly important in the CO2 sequestration process as injected CO2 first moves through the cleat system, which eventually changes the coal's permeability and strength. The main objective of this study is to investigate the effects of cleat density and direction on the strength reduction of coal with CO2 adsorption. A series of strength experiments was conducted on non-CO2-saturated and CO2-saturated (1, 2, 3 and 16 MPa) coal samples with two different cleat densities (low-rank lignite and high-rank bituminous) and two different cleat angles (around 20 and 70 to the loading directions). According to the experimental results, CO2 saturation, at up to 3 MPa saturation pressure, causes up to 4.5 times higher strength reduction in bituminous coal (43%) compared to lignite (9.6%). The compressive strength reduction percentage in coal shows a linearly increasing trend with CO2 saturation pressure (1-3 MPa), where the slope is significantly higher for bituminous coal (15.3) compared to lignite (3.2). When the cleat direction reduces from 70 to 20, the CO2 adsorption (at 16 MPa) induced UCS strength reduction in bituminous coal reduces by around 20%. It is interesting to report that cleat density and direction do not exhibit a significant influence on elastic modulus reduction in coal compared to the strength reduction. (C) 2012 Elsevier Ltd.
The effect of bedding structure on mechanical property of coal
DOI:10.1016/j.mser.2015.04.001
URL
PMID:27134415
[Cited within: 1]

Over the past century, hydrogels have emerged as effective materials for an immense variety of applications. The unique network structure of hydrogels enables very high levels of hydrophilicity and biocompatibility, while at the same time exhibiting the soft physical properties associated with living tissue, making them ideal biomaterials. Stimulus-responsive hydrogels have been especially impactful, allowing for unprecedented levels of control over material properties in response to external cues. This enhanced control has enabled groundbreaking advances in healthcare, allowing for more effective treatment of a vast array of diseases and improved approaches for tissue engineering and wound healing. In this extensive review, we identify and discuss the multitude of response modalities that have been developed, including temperature, pH, chemical, light, electro, and shear-sensitive hydrogels. We discuss the theoretical analysis of hydrogel properties and the mechanisms used to create these responses, highlighting both the pioneering and most recent work in all of these fields. Finally, we review the many current and proposed applications of these hydrogels in medicine and industry.
Mechanical properties of coal microcomponents under continuous indentation
DOI:10.1134/S1062739116041382 URL [Cited within: 1]
Effects of bedding on the dynamic indirect tensile strength of coal: Laboratory experiments and numerical simulation
DOI:10.1016/j.coal.2014.08.007
URL
[Cited within: 1]

Dynamic indirect tensile tests were carried out by using a Split Hopkinson Pressure Bar (SHPB) for coal sampled from the Datong mine in China. The principal purpose was to explore the influence of bedding structure in the coal on its dynamic indirect tensile strength. However, to resolve some contradictions, X-ray micro CT, high speed optical imaging and a discrete element based modelling approach were combined to analyze the test results. The X-ray micro CT was used to detect the actual bedding structure in the coal; the high speed imaging captured failure patterns of the specimens with different bedding directions; and the numerical modelling was utilized to investigate the influence of different bedding structures on dynamic strength. The SHPB and numerical results illustrate that dynamic indirect tensile strength reliably correlates with impact velocity. In addition, the dynamic indirect tensile strength is not only influenced by the bedding direction but also by the roughness and discontinuity of the bedding. Based on these findings, a method is developed to further process the test data including a model to describe the dynamic indirect tensile strength of Datong coal. (C) 2014 Elsevier B.V.
Different bedding loaded coal mechanics properties and acoustic emission
DOI:10.1007/s12665-017-7169-5 URL [Cited within: 1]
Influence of bedding and cleats on the mechanical properties of a hard coal
A hydraulic fracture height mathematical model considering the influence of plastic region at fracture tip
Hydraulic fracturing accelerates coalbed methane recovery
The progressive fracture of Lac du Bonnet granite
Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations
DOI:10.1016/j.ijrmms.2004.02.001
URL
[Cited within: 1]

Abstract
The rock mass failure process is characterized by several distinct deformation stages which include crack initiation, crack propagation and coalescence. It is important to know the stress levels associated with these deformation stages for engineering design and practice.
Extensive theoretical, experimental and numerical studies on the failure process of intact rocks exist. It is generally understood that crack initiation starts at 0.3 to 0.5 times the peak uniaxial compressive stress. In confined conditions, the constant-deviatoric stress criterion was found to describe the crack initiation stress level.
Here, generalized crack initiation and crack damage thresholds of rock masses are proposed. The crack initiation threshold is defined by σ1−σ3=Aσcm and the crack damage threshold is defined by σ1−σ3=Bσcm for jointed rock masses, where A and B are material constants and σcm is the uniaxial compressive strength of the rock masses. For a massive rock mass without joints, σcm is equal to σcd, the long-term uniaxial strength of intact rock. After examining data from intact rocks and jointed rock masses, it was found that for massive to moderately jointed rock masses, the material constants A and B are in the range of 0.4 to 0.5, 0.8 to 0.9, respectively, and for moderately to highly jointed rock masses, A and B are in the range of 0.5 to 0.6, 0.9 to 1.0, respectively. The generalized crack initiation and crack damage thresholds, when combined with simple linear elastic stress analysis, assist in assessing the rock mass integrity in low confinement conditions, greatly reducing the effort needed to obtain the required material constants for engineering design of underground excavations.
The influence of rock fabric on excavation damage in the Lac du Bonnett granite
DOI:10.1016/j.ijrmms.2004.09.013
URL
[Cited within: 1]

Abstract
This paper documents the contribution of rock fabric on excavation damage development in the granite of the Lac du Bonnet Batholith (LDBB). It is concluded that the LDBB contains structural elements and distinct textural varieties which differ significantly in their response to rock properties testing and to excavation. Data collected in this study demonstrate the highly heterogeneous internal structure characteristic of apparently homogenous batholiths, and the influence of this heterogeneity on rock mass response. Evidence for anisotropy of the rock mass is demonstrated to have occurred on the geological time-scale, and its influence is still present in recent excavations. This anisotropy exists at a wide range of scales, from the localization of fault zones along low-dipping layering at the kilometre-scale, to the localization of failure around tunnels by separation along this and other weakness directions.
A modified Hoek-Brown failure criterion for anisotropic intact rock
DOI:10.1016/j.ijrmms.2007.05.004
URL
[Cited within: 1]

Abstract
The Hoek–Brown criterion parameters (σci, mi and s) are significantly influenced by the strength anisotropy of intact rock. In the present study, the criterion was modified by incorporating a new parameter (kβ) to account for the effect of strength anisotropy, thus being able to determine the strength of intact anisotropic rock under loading in different orientations of the plane of anisotropy. The range of the parameter (kβ) for the rocks tested has been analytically investigated by carrying out triaxial tests, in different orientations of the foliation plane. The proposed modification was studied for metamorphic rocks (gneiss, schist, marble), but could also be applied to other rock types exhibiting “inherent” anisotropy, e.g. sedimentary as well as igneous rocks. The proposed modified criterion is intended for use for prediction of strength of intact rock, but can also be extended to rock masses.
Frequency of earthquakes in California
Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value