Introduction
The matrix permeability of deep complex carbonate, volcanic and tight clastic reservoirs in China is generally low, and fractures play a leading role in oil and gas flow in these reservoirs. Accurate identification and quantitative evaluation of fractures are of great significance for oil and gas exploration[1,2,3,4]. The main fracture evaluation methods include dual lateral resistivity difference method, high-resolution electrical imaging method and Stoneley wave attenuation method[5,6,7,8,9,10,11]. With respect to the dual lateral logging response characteristics of fractured reservoirs, researchers have carried out many theoretical and numerical simulations and proposed a quantitative fracture evaluation method based on the difference of dual lateral resistivity[5,6,7]. Because the difference of dual lateral resistivity is affected not only by fractures, but also by formation water salinity, resistivity of drilling fluid, and matrix permeability etc., the accuracy of the fracture quantitative evaluation by the difference of dual lateral resistivity is low. High-resolution electrical imaging logging has been widely used in reservoir fracture evaluation[8,9,10]. However, in the cases that the reservoir has argillaceous interlayers or fractures are filled with low resistivity materials, it is difficult to identify true and false fractures and tell the effectiveness of fractures by electrical imaging logging. In addition, electrical imaging logging also faces challenges in the evaluation of micro-fracture and fracture radial extension. Stoneley wave attenuation is widely used in quantitative evaluation of reservoir fractures. Li first carried out the phase relation study of first arrival waves of different modes through full wave measurements and found that the phase of first arrival Stoneley wave is the same as that of the first arrival P-wave, but opposite to that of the first arrival S-wave[11]. The results provided a solid foundation for the extraction of Stoneley first arrival wave amplitude and further evaluation of fractures by using Stoneley wave. Hornby et al. proposed fracture width evaluation method by Stoneley wave based on simplified flat fracture model[12]. Kostek et al. further studied the characteristics of Stoneley wave reflections to fractures with different widths under the condition of borehole enlargement[13,14]. Tang et al. proposed a Stoneley wave field separation method and analyzed the influence of reservoir permeability on the attenuation of Stoneley wave[15,16]. However, due to the difficulty of low-frequency Stoneley wave excitation, the experimental study of Stoneley wave attenuation is still very limited.
A shock tube is an experimental device which is used to measure the acoustic properties of full diameter core in the tube by exciting shock wave. The acoustic waves excited by the shock tube device cover a broad frequency band (0.5-160.0 kHz). The measured waveforms include the main borehole mode waves of acoustic logging, especially the low-frequency Stoneley wave. The shock tube provides a reliable experimental means for the study of Stoneley wave attenuation law[17]. Smeuders et al. studied the acoustic characteristics of partially and fully water saturated rock samples by using the shock tube device[18]. Fan et al. studied the influence of fractures in water saturated cores on Stoneley wave[19]. However, they all used artificial cores in their experiments. Li et al. carried out shock tube experiments and theoretical analysis on real carbonate cores to figure out the influence of horizontal fractures with different widths on Stoneley wave[20]. In order to further simulate the real underground formation condition, this paper introduces a modified shock tube experimental device and a manufacture method of complex fracture model. Through the shock tube experiments of Stoneley wave under different fracture conditions, the influences of fracture width, dip angle, extension and filling material on Stoneley wave attenuation are studied.
1. Experiments
1.1. Experimental device
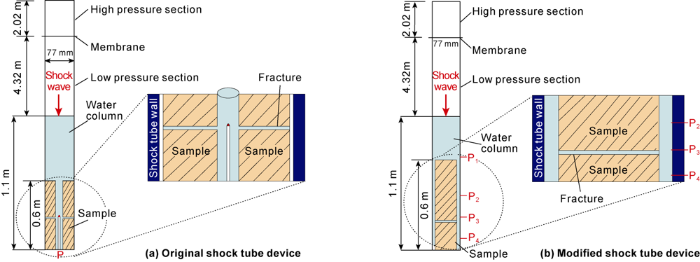
The original shock tube device is shown in Fig. 1a. The core sample with a borehole in the center is placed at the bottom of the shock tube. The Stoneley wave is measured by the movement of a mobile probe in the borehole. There are two difficulties in the original device: firstly, it is difficult to drill a borehole in the middle of the real carbonate core, as the core can break during the borehole drilling; secondly, there is only one measuring probe in the borehole, which may not calibrate and correct the measured data, resulting in large error. To solve these problems, a modified shock tube device has been introduced in this paper (Fig. 1b): a screw gear with the system accuracy of 0.1 mm is installed at the bottom of the core sample to accurately control the movement of the core up and down; four fixed probes P1, P2, P3 and P4 are installed on the wall of the shock tube, among which P2, P3 and P4 are used to measure Stoneley wave signals at different positions of the core. The distance between P1 and P2 is 30 cm. The distances between P2 and P3, P3 and P4, are both 20 cm. In the experiment, probe P1 is always located at the shock tube wall above the core sample, while probes P2, P3 and P4 are located at the shock tube wall on lateral side of the core sample. The measurement signal of probe P1 can be used to correct the time and amplitude of Stoneley waves measured by probes P2, P3 and P4, to effectively improve the signal-to-noise ratio of the first arrival Stoneley wave and the measurement accuracy. The core sample position is changed by the screw gear in the modified device, so it is not necessary to drill the borehole in the core sample, and it is convenient to manufacture the fracture models for the experiments which has a beneficial for Stoneley wave measurement of real cores. In order to ensure that the probe P3 can measure the Stoneley waves above and below the fracture, the height of the sample is set to 60 cm, and the distance between the fracture center and the sample top is set to 40 cm.
Fig. 1.
Fig. 1.
Schematic diagram of shock tube experimental device.
During the experiment, degassed water was filling into the shock tube to form a water column with a height of 1.1 m, and a Polyethylene terephthalate (PET) membrane was installed at 4.32 m above the water surface to separate the upper high-pressure air section and the lower atmospheric air section (Fig. 1). Then the whole system was standing still for 2-5 d. When the core was completely saturated with water, the experiment could be started. During the measurement, the membrane was ruptured by an electrified metal ring, so that the high- pressure air section and the atmospheric air section were connected instantaneously to generate the shock wave. The shock wave went onto the upper water column to generate a uniform and stable plane wave. When the plane wave propagated downwards, part of it reflected from the top surface of the sample, the rest of the energy went into the annulus between the sample and the shock tube wall to generate Stoneley wave (Fig. 1b). Probes P1, P2, P3 and P4 recorded the pressure varying with time at four different positions. By rotating the screw gear, the piston pushed the core sample moving up 5 mm. The membrane was replaced and the experiment procedure was repeated. Another four series of signals were recorded by the four probes. By moving the core sample several times, the fractures in the sample could gradually pass through the probe P3, and multiple sets of measurement signals could be obtained. The number of times for the core moving upwards depended on the size of the core. In this paper, all the samples moved upwards for 15 times. In addition, the probe P3 could obtain measurement signals below and above the fracture to record the waveforms of Stoneley wave before and after passing through the fracture. The waveforms obtained by P3 were the keys in this paper.
1.2. Manufacture of fracture models
1.2.1. Fracture models with different widths
Superposition method is an important method to make fracture model. However, the support occupies a large proportion of fracture space in the model made by this method, and the support itself has a great influence on the Stoneley wave measurement results. Therefore, this paper proposed a method of making fracture models with different widths by using point supports. For the fracture small in width, small balls were used as the supports, and the diameter of the small ball was equal to the fracture width (Fig. 2a). For the fracture large in width, a cylinder in the middle and two hemisphere at both ends were used as supports. The fracture models with specific widths were made by adjusting the height of the middle cylinder (Fig. 2b). When there was no support in the middle of the fracture, the fracture was closed and was approximately zero in width. In this paper, six horizontal fracture models with widths of 0, 2, 4, 6, 10 and 30 mm were made by using full diameter carbonate cores. The above method of making fracture models with different widths could not only ensure the point contact between the supports and the two surfaces of the fracture, minimize the volume of the supports and their effects on the experimental results, but also maintained the stability of the model and the consistency of the fracture width at different positions by determining the proper number and position of supports.
Fig. 2.
Fig. 2.
Fracture models with different widths made by using point supports.
1.2.2. Fracture models with different dip angles
In order to quantify the effect of fracture dip angle on Stoneley wave attenuation, three fracture models with dip angles of 0°, 16° and 70° were manufactured. The full diameter carbonate sample with two natural fractures was used as the fracture models with dip angles of 0° and 16°. The fracture model with dip angle of 70° was made from the same carbonate sample artificially.
For the fracture model with low angle, three small balls were selected as supports. The diameter of the ball was the same as the width of the fracture. Fig. 3a shows the low angle fracture model with a dip angle of 16° and a width of 6 mm made from the full diameter carbonate rock sample with a natural fracture. The fracture model with high angle was difficult to make if small balls were used as supports for stable problem. Two gaskets were used to support the fracture in the model. The thickness of the gasket was equal to the width of the fracture. The diameter of the gasket was 5 mm. Fig. 3b shows the high angle fracture model with the dip angle of 70° and width of 6 mm.
Fig. 3.
Fig. 3.
Fracture models with the same width and different dip angles.
1.2.3. Fracture models with different extension lengths
The extension length of different fractures in formations is different. In order to determine the effect of fracture extension length on Stoneley wave attenuation, three fracture models with the same fracture width of 2 mm and different extension lengths of 4, 14 and 24 mm were made using full diameter carbonate cores. Fig. 4 shows a fracture model with the fracture width of 2 mm and extension length of 14 mm. Because the diameter of the core used in this paper is 68 mm, the horizontal fracture model with fracture width of 2 mm can be regarded as a fracture model with 2 mm in fracture width and 34 mm in fracture extension length during data analysis.
Fig. 4.
Fig. 4.
Fracture model with width of 2 mm and extension length of 14 mm.
1.2.4. Fracture models with different filling materials
Fractures in reservoirs are usually filled with argillaceous, calcareous or other mineral components at different degrees. Different fillings have different influences on fracture effectiveness. In order to study the effects of different filling materials on Stoneley wave attenuation, a full-diameter carbonate core was used to make fracture models with different filling materials and carried out shock tube experiments.
In order to measure the effect of different filling materials on attenuation of Stoneley wave amplitude accurately, it is necessary to ensure that the matrix and other fracture parameters of different fracture models are consistent. For this reason, the following manufacturing methods are proposed. Firstly, an annular filling material with an inner diameter of 44 mm, outer diameter of 68 mm and width of 6 mm was made (Fig. 5a). Secondly, a cylindrical shim with diameter of 44 mm and width of 6 mm was made from the carbonate rock core and placed in the center of the annular filling material to form an assembly. Finally, the above combination was embedded into the fracture of carbonate rock core to form a fracture model with specific filling material as shown in Fig. 5b. In our experiments, Bentheimer sandstone, Felser sandstone and PVC (polyvinyl chloride) materials were used to manufacture three different filling fracture models. In order to investigate the influence of filling permeability, the porosities of the two kinds of selected sandstones are both 21%. The permeability difference was three orders of magnitude, specifically, the permeabilities of the Bentheimer sandstone and Felser sandstone were 1001.3×10-3 μm2 and 1.802×10-3 μm2 respectively.
Fig. 5.
Fig. 5.
Fracture model with filling materials.
In this way, 21 sets of fracture models with different parameters were manufactured using full diameter carbonate cores (Table 1). In Table 1, A1-A6 models represent horizontal fractures models with different widths. B1-B3 models represent fracture models with 2 mm width and different dip angles. C1-C3 models represent fracture models with 6 mm width and different dip angles. D1-D5 models represent fracture models with different extensions. E1-E4 models represent fracture models with different filling materials.
Table 1 21 sets of fracture models and main parameters.
| Model No. | Dip angle/(°) | Width/ mm | Extension/ mm | Filling material |
|---|---|---|---|---|
| A1 | 0 | 0 | Breakthrough | Water |
| A2 | 0 | 2 | Breakthrough | Water |
| A3 | 0 | 4 | Breakthrough | Water |
| A4 | 0 | 6 | Breakthrough | Water |
| A5 | 0 | 10 | Breakthrough | Water |
| A6 | 0 | 30 | Breakthrough | Water |
| B1 | 0 | 2 | Breakthrough | Water |
| B2 | 16 | 2 | Breakthrough | Water |
| B3 | 70 | 2 | Breakthrough | Water |
| C1 | 0 | 6 | Breakthrough | Water |
| C2 | 16 | 6 | Breakthrough | Water |
| C3 | 70 | 6 | Breakthrough | Water |
| D1 | 0 | 2 | 0 | Water |
| D2 | 0 | 2 | 4 | Water |
| D3 | 0 | 2 | 14 | Water |
| D4 | 0 | 2 | 24 | Water |
| D5 | 0 | 2 | Breakthrough | Water |
| E1 | 0 | 6 | 12 | Water |
| E2 | 0 | 6 | 12 | Bentheimer sandstone |
| E3 | 0 | 6 | 12 | Felser sandstone |
| E4 | 0 | 6 | 12 | PVC |
2. Data processing
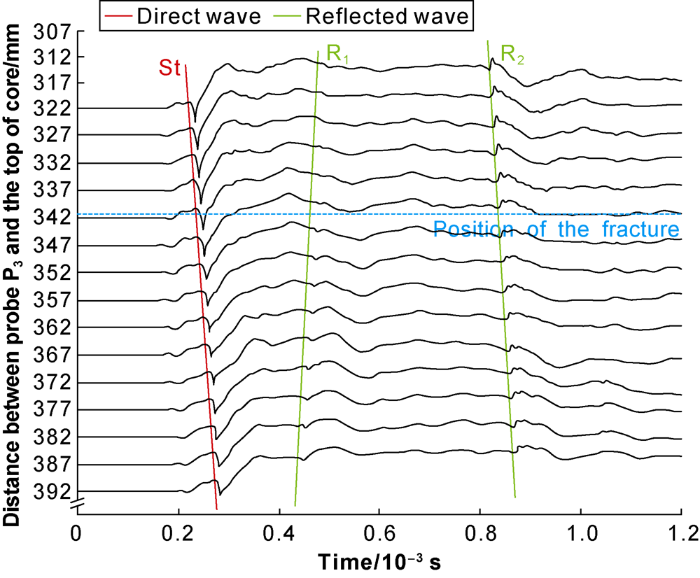
Stoneley wave measurements were carried out on 21 groups of carbonate fracture models in Table 1 by using the modified shock tube experimental device in Fig. 1b. Fig. 6 shows the 15 waveforms of model A4 recorded by probe P3. All the measured signals have been corrected in time, for each channel the record time begins when the sound wave first reaches the top of the core. According to the sequence of arrival time, the direct Stoneley wave (St) and reflected Stoneley wave (R1, R2) can be observed in the figure. The reflected Stoneley wave R1 is from the bottom of the core sample. The reflected wave R2 is the Stoneley wave generated by the expansion wave reflected downward from the water-air interface. The direct Stoneley wave St is focused and discussed in this paper.
Fig. 6.
Fig. 6.
Waveforms of the horizontal fracture model with 6 mm wide measured by probe P3.
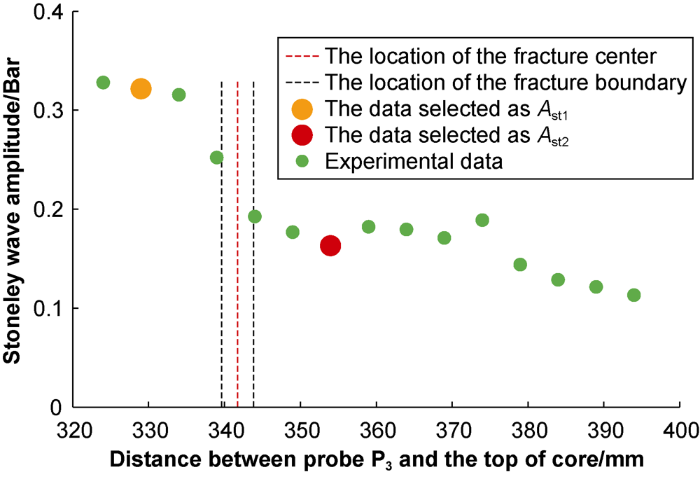
It can be seen from Fig. 6 that the amplitude of Stoneley wave decreases significantly after passing through the fracture. In this paper, the amplitude of Stoneley wave is defined as the difference between the wave peak and the wave trough. The Stoneley wave amplitudes of the 15 waveforms in Fig. 6 are shown in Fig. 7. In Fig. 7, the data points on the left side of the red dotted line are the amplitudes of Stoneley wave above the fracture (that is before Stoneley wave passes through the fracture). The data points on the right side of the red dotted line are the amplitudes of Stoneley wave below the fracture (that is after Stoneley wave passes through the fracture). Fig. 7 shows that Stoneley wave attenuates before reaching and after passing a certain range of the fracture. In other words, the influence of the fracture on Stoneley wave is not limited to the location of the fracture, but exists in a region near the fracture.
Fig. 7.
Fig. 7.
Variations of Stoneley wave amplitudes at different distances.
In order to quantitatively describe the attenuation law of Stoneley wave, the relative amplitude of Stoneley wave is defined:
Rst eliminates the interference factors (such as the difference of core matrix properties) and can reflect the influence of fracture on Stoneley wave more accurately. The closer the Rst value to 1, the smaller the attenuation of Stoneley wave caused by the fracture is. The closer the Rst value to 0, the larger the attenuation of Stoneley wave caused by the fracture is.
Accurately determining the amplitudes Ast1 and Ast2 is crucial to quantitative calculation of the relative amplitude Rst by using Eq. (1). For a horizontal fracture, the analysis results of experimental data show that it is appropriate to take the amplitude of Stoneley wave at the 10 mm above the upper end of the fracture as Ast1, and the amplitude of Stoneley wave at the 10 mm below the lower end of the fracture as Ast2. In Fig. 7, the red dotted line is the location of the fracture center, the blue dotted lines on both sides are the location of the fracture boundaries. The orange and red data points on the left and right sides of the fracture represent the Ast1 and Ast2 determined according to the proposed method.
For an inclined fracture, the amplitude at 10 mm above the upper end of the fracture is still taken as the amplitude Ast1. But as the amplitude decreasing of Stoneley wave after passing through the fracture is related to the fracture dip angle, Ast2 cannot be fixed as the amplitude at 10 mm below the lower end of the fracture. The experi-mental data analysis shows that the calculated Ast2 is most reasonable when the distance L between the position where Ast2 is obtained and the lower end of the fracture satisfies the following equation:
If there is no measurement point at the position L below the lower end of the fracture, the value of point nearest to this position is selected as Ast2.
3. Data analysis
3.1. The influence of fracture width
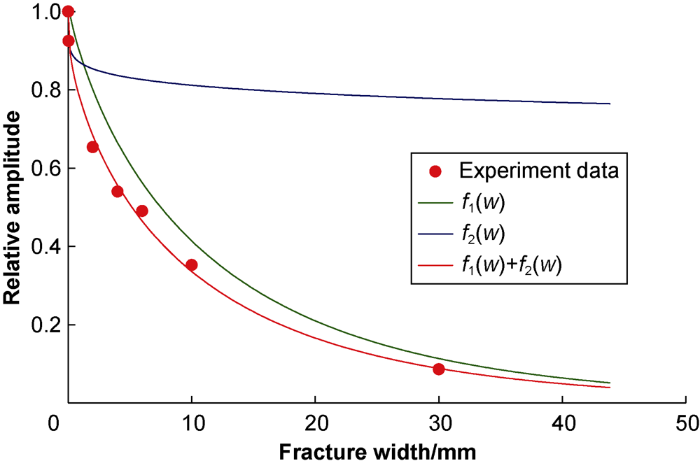
Fig. 8 shows the variations of the relative amplitude of Stoneley wave under different fracture widths. It can be seen from this figure that with the increase of fracture width, the Stoneley wave decreases in relative amplitude after passing through the fracture, but the decreasing rate gradually slows down. For example, the relative amplitude of Stoneley wave drops by 0.648 when the fracture width goes up from zero to 10 mm. It means that the relative amplitude decreases by 0.064 with the increase of unit fracture width (1 mm). When the fracture width goes up from 10 mm to 30 mm, the relative amplitude of Stoneley wave drops by 0.266, which means that the relative amplitude only decrease by 0.013 with the increase of unit fracture width (1 mm).
Fig. 8.
Fig. 8.
Variations of Stoneley wave relative amplitude at different fracture widths.
The experimental data show that the relation between the relative amplitude of Stoneley wave Rst and fracture width Wf is:
The constant a1 is 1.021, b1 is -0.143, n1 is 0.810, n2 is 0.170. The red solid line in Fig. 8 is plotted according to Eq. (3). It can be seen that almost all the experimental data points are on the red curve, indicating that Eq. (3) accurately describes the influence of fracture width on Stoneley wave amplitude. There are two items in the exponential part of Eq. (3), the Eq. (3) can be re-written as:
Eq. (4) shows that the effect of fracture width on Stoneley wave attenuation consists of two parts ${{f}_{1}}\left( w \right)$ and ${{f}_{2}}\left( w \right)$, where${{f}_{1}}\left( w \right)={{a}_{1}}{{\text{e}}^{-0.143{{w}^{0.81}}}}$ and ${{f}_{2}}\left( w \right)=$ ${{\text{e}}^{-0.143{{w}^{0.17}}}}$ in this paper. The variations of ${{f}_{1}}\left( w \right)$ and $f_{2}(w)$ with fracture width are plotted as the green and blue solid lines in Fig. 8, respectively. It can be seen from this figure, the $f_{1}(w)$. represents the main part of the fracture's influence on Stoneley wave, which decays exponentially with the increase of fracture width. The $f_{2}(w)$ represents the relatively small influence of fracture on Stoneley wave, and its value tends to be stable with gradual increase of fracture width.
3.2. The influence of fracture dip angle
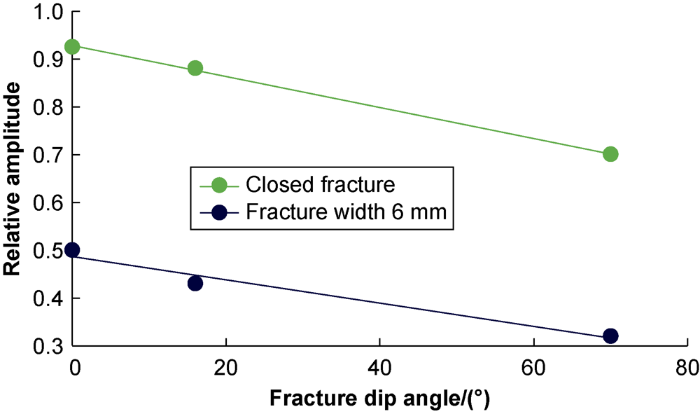
Fig. 9 shows the relative amplitudes of Stoneley wave after passing a closed fracture and 6 mm wide fracture at three different dip angles of 0°, 16° and 70°. It can be seen for either the closed fracture or the fracture of 6 mm wide, the relative amplitude of Stoneley wave after passing through the fracture decrease linearly with the increase of dip angle. The reason is that when the fracture dip angle increases, the fracture cross-sectional area also becomes larger, so the energy diffusion of Stoneley wave caused by the fracture increases, the attenuation of Stoneley wave becomes stronger, and the relative amplitude of Stoneley wave decreases.
Fig. 9.
Fig. 9.
Variations of Stoneley wave relative amplitude with different fracture angles.
The experimental results show that the linear relation between the relative amplitude of Stoneley wave and fracture dip angle is as follows:
For the fracture models of full diameter carbonate rock core used in this paper, a2 is -0.003 and c2 is 0.928 in Eq. (5) when the fracture is naturally closed (width is 0); a2 is -0.002 and c2 is 0.487 in Eq. (5) when the fracture width is 6 mm. The results show that, the values of a2 of different-width fracture models with the same matrix are very similar. In other words, with the increase of fracture dip angle, the slopes of linear decrease of relative amplitude are basically the same. The value of c2 is the same as the relative amplitude of Stoneley wave after passing through the horizontal fracture with the same width.
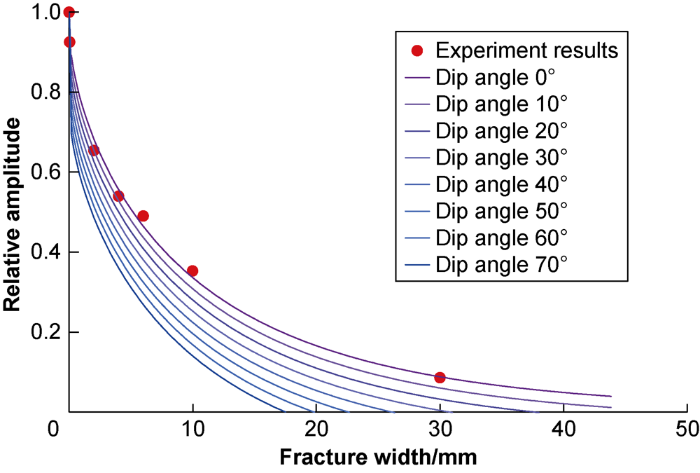
By using Eq. (5), the experimental results of Stoneley wave relative amplitude of horizontal fractures with different widths in Fig. 8 can be interpolated to get the relative amplitudes of Stoneley wave after passing through fractures with different widths and different dip angles. The interpolation results are plotted in Fig. 10. The abscissa is the width of the fracture, the ordinate is the relative amplitude of Stoneley wave. The curves in different colors represent the relative amplitudes of Stoneley wave at different fracture dip angles.
Fig. 10.
Fig. 10.
Relative amplitudes of Stoneley wave at different widths and dip angles of fractures.
3.3. Effect of fracture extension length
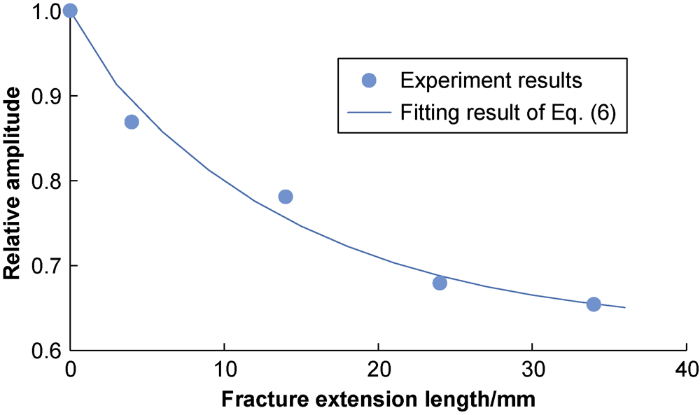
Due to the influence of formation lithology, in-situ stress and other factors, the radial extension lengths of fractures in reservoirs are different. The experimental results of the influence of fracture extension length on Stoneley wave attenuation is plotted in Fig. 11. It can be seen that: (1) with the increase of fracture extension length, the Stoneley wave decreases in relative amplitude and increases in attenuation degree; (2) with the increase of fracture extension length, the decreasing speed of the Stoneley wave relative amplitude reduces. The experimental data analysis shows that the relation between the relative amplitude of Stoneley wave and the fracture extension length is:
Fig. 11.
Fig. 11.
Variation of relative amplitude of Stoneley wave at different fracture extension lengths.
When the fracture extension length d is zero, the Rst is 1.0, the parameters a3 and c3 are not independent in this case, and the sum of them is 1.0. For the fracture models with different extension lengths, the parameters a3, b3 and c3 are 0.364, -0.072 and 0.636 respectively.
3.4. Influence of fracture filling material
In order to study the influence of fracture filling material on Stoneley wave attenuation, Stoneley waves passing four fracture models with different filling materials were measured (Table 1). Model E1 represents the case that the fracture with no solid filling material but full of water. In this case, the fracture has the highest permeability. Models E2 and E3 represent the cases of fractures filled with Bentheimer sandstone (with the permeability of 1001.305× 10-3 μm2) and Felser sandstone (with the permeability of 1.802×10-3 μm2), respectively. Model E4 represents the case with the fracture filled with non-porous PVC material near zero in permeability. Table 2 shows the relative amplitudes of Stoneley waves after passing through the fractures in 4 cases. The Stoneley wave decrease in relative amplitude gradually and increases in attenuation gradually with the increase of filling material permeability. The reason is that, as the filling material permeability goes up, the energy diffusion of Stoneley wave passing through the fracture increases, and the attenuation of the Stoneley wave caused by the fracture increases. Therefore in the actual formations, if a fracture is unfilled or partially filled and thus high in permeability, its influence on Stoneley wave is significant. If a fracture is completely filled by tight material (such as calcium), it has little influence on Stoneley wave amplitude.
Table 2 Experimental results of Stoneley wave after passing fractures filled by different materials.
| Model No. | Filling material | Permeability/ 10-3 μm2 | Relative amplitude |
|---|---|---|---|
| E1 | Water | 0.597 | |
| E2 | Bentheimer sandstone | 1 001.305 | 0.709 |
| E3 | Felser sandstone | 1.802 | 0.769 |
| E4 | PVC | 0.835 |
3.5. Influence intensities of different fracture factors
The experimental results show that the relative amplitude Rst of Stoneley wave exponentially decreases with the increase of fracture width and extension length, and the quantitative relationships between them meet the Eq. (3) and Eq. (6) respectively. In Eq. (3), parameter b1 reflects the influence intensity of fracture width on the relative amplitude of Stoneley wave, while parameter b3 in Eq. (6) reflects the influence intensity of fracture extension length on the relative amplitude of Stoneley wave. The experimental results show that the absolute value of parameter b1 is much larger than that of parameter b3, so the effect of fracture width on Stoneley wave is more significant than the extension length.
In order to compare the relative influence intensity between fracture filling material and fracture extension length, it is assumed that there is a single fracture in the model. When the fracture extension length becomes the largest and there is no filling material, the relative amplitude of Stoneley wave after passing through the fracture is Rst. If the fracture extension length is zero or the fracture is completely filled by impermeable material, the relative amplitude of Stoneley wave is 1. Therefore, the maximum variations of Stoneley wave relative amplitudes caused by extension length and filling material of the fracture are both (1-Rst), and the influence intensities of them are similar.
With the increase of fracture dip angle, the relative amplitude of Stoneley wave decreases linearly according to Eq. (5), and the slope (parameter a2) of the linear decrease is not affected by fracture width. The maximum variation of Stoneley wave relative amplitude is only 0.27 when the fracture dip angle changes from 0° to 70°. The influence intensity of fracture dip angle on Stoneley wave attenuation is the lowest compared with other fracture parameters.
Based on the above analysis, the fracture width has the greatest influence on the relative amplitude of Stoneley wave, followed by the fracture extension length and permeability of filling material, and finally the fracture dip angle.
4. Conclusions
The Stoneley wave measurements of full diameter core with different fracture conditions are carried out by using the improved shock tube device. The signal-to-noise ratio of the first arrival Stoneley wave and the measurement accuracy can be effectively improved. The influence of fracture on Stoneley wave exists in a certain range before and after the Stoneley wave reaches the fracture. The relative amplitude defined in this paper can accurately characterize the attenuation of Stoneley wave after passing through different fractures. The relative amplitude of Stoneley wave decreases exponentially with the increase of fracture width. The influence of fracture width on the relative amplitude of Stoneley wave can be expressed as two parts. The first part is the primary part of the influence of fracture on Stoneley wave, and the second part has less influence on Stoneley wave. With the increase of fracture dip angle, the relative amplitude of Stoneley wave decreases linearly. With the increase of fracture extension length, the relative amplitude of Stoneley wave decreases exponentially. The relative amplitude of Stoneley wave decreases with the increase of filling material permeability. Among the four factors, fracture width, dip angle, extension length and filling material, the fracture width has the greatest influence on the relative amplitude of Stoneley wave, followed by the fracture extension length and permeability of filling material, and finally the fracture dip angle.
Nomenclature
a1, a2, a3, b1, b3, c2, c3—constants, dimensionless;
Ast1—the amplitude of Stoneley wave before passing the fracture, Bar;
Ast2—the amplitude of Stoneley wave after passing the fracture, Bar;
a1, a2, a3, b1, b3, c2, c3—constants, dimensionless;
d—fracture extension length, mm;
f1(w)—the main part of the fracture's influence on Stoneley wave;
f2(w)—the second part of the fracture's influence on Stoneley wave;
L—the distance between the position where Ast2 was read and the lower end of the fracture, mm;
Rst—the relative amplitude of Stoneley wave, dimensionless;
w—fracture width, mm;
θ—fracture dip angle, (°).
Reference
Production prediction for fracture-vug carbonate reservoirs using electric imaging logging data
Grading evaluation and prediction of fracture-cavity reservoirs in Cambrian Longwangmiao Formation of Moxi Area, Sichuan Basin, SW China
Prediction of gas production in carbonates based on CT analysis and nuclear magnetic resonance (NMR) logging
The dual laterolog response in fractured rocks
Experimental studies and investigations on the dual lateral log response of near borehole fractures
Simulation and quantitative evaluation of dul-laterolog responces of fracture in low resistivity carbonate reservoir
Quantitative characterization of volcanic fracture distribution based on electrical imaging logging: A case study of Carboniferous in Dixi Area, Junggar Basin
Quantitative fracture evaluation method based on core-image logging: A case study of Cretaceous Bashijiqike Formation in KS2 well area, Kuqa Depression, Tarim Basin, NW China
Extracting fracture-vug plane porosity from electrical imaging logging data using dissection of wavelet-transform-based image
Interpretation of the experimental phenomena about the P and S head wave phase relations, and its significance to full wave logging
Fracture evaluation using reflected Stoneley-wave arrivals
The interaction of tube waves with borehole fractures, Part I: Numerical models
The interaction of tube waves with borehole fractures, Part II: Analytical models
Quantitative borehole acoustic methods
Fast inversion of formation permeability from Stoneley wave logs using a simplified Biot Rosenbaum Model
Measurement of shock-induced guided and surface acoustic waves along boreholes in poroelastic materials
Wave propagation in porous media containing a dilute gas-liquid mixture: Theory and experiments
Shock-induced borehole waves and fracture effects
Shock-induced Stoneley waves in carbonate rock samples