Introduction
Since Strebelle boosted the efficiency of multi-point geostatistics modeling by means of search tree[1], the multi-point geostatistics has been widely applied in reservoir modeling. With the advantages of conditionalization of two-point statistics and morphologization of modeling target, this method has achieved good modeling effect[2,3,4,5,6,7,8,9]. On this basis, many scholars have conducted research and improvement of this method. Arpat came up with pattern-based geostatistical sequential simulation (Simpat)[10], Zhang et al. brought forward Filtersim algorithm[11] to increase the computational efficiency; Honarkhah et al. proposed Dispat algorithm[12] by way of K-means clustering; and Mariethoz et al. came up with the DS algorithm by replacing the 1st pattern living up to error expectations as the optimal pattern based on the idea of the most similar matching[13]. As the core input parameter, the training image directly determines the accuracy of geological model[14,15,16]. Nevertheless, in practical application, it is difficult to acquire a 3D training image displaying the structure of actual underground reservoir as well as its distribution characteristics, and currently, it is also a hot issue in the research on multi-point geostatistics[17,18,19,20,21]. In the course of geological research, it has become a conventional method to build a reservoir pattern to guide the dissection of underground reservoir by integrating all sorts of geological information, this method can interpret and analyze the 2D distribution of reservoirs from the perspective of sedimentology pretty well, and meet the actual data simultaneously. After digitizing, the 2D cross-sections become 2D training images of multi-point geostatistics. Thus, how to re-build a 3D geological model with 2D training images has become a research direction of multi-point geological modeling[22,23,24,25,26,27,28]. Okabe et al. aggregated the 2D thin slice information of carbonate rocks by linear pooling formula, and reproduced the 3D pore model with macro scale[22,23]. On this basis, quite a number of researchers tried to directly re-build 3D models with low-dimensional data[24,25,26]. Comunian et al.[25] proposed a 2D sequential simulation method (s2Dcd) in 2012. In 2018, Chen et al. brought forward a local search strategy on the basis of s2Dcd method[28], which searched the sub-sections near the simulation points for estimation, with fairly good results achieved. However, for the reservoir with unstable distribution, the repeatability of spatial pattern decreases with the shrinkage of sub-section. In practical application, it is rather difficult to acquire a stable probability distribution, so the sampling uncertainty increases. Although the stability of probability distribution can be enhanced by adding slices, this also increases the workload simultaneously. To address this issue, this thesis improves the local search method and simulation strategy holding the idea of adaptive spatial resampling in seismic inversion[29]: in the first step, re-build the simulation path with reference to conditional data, and give priority to the areas with much conditional data; next, analyze the sampling confidence of the previous simulation results, retain some credible data and add them to the conditional data, and re-simulate the areas outside the conditional data, in a bid to boost the accuracy of model prediction. After testing the improved method with theoretical model, it is applied to a block in Canada, and the geological model of lateral accumulation layer of meandering river under the influence of tide is set up, and the modeling results are compared with the actual data and geological analysis results.
1. Principle and improvement of the method
In 2012, Comunian et al. came up with the method of re-building a 3D model on the basis of 2D cross-section[25]. The idea is to scan several orthogonal 2D training images to acquire statistical information in all directions, and then get a 3D probability distribution by taking a fusion strategy, to finally fulfill the purpose of re-building a 3D model. On the basis of this method, Chen et al. narrowed the area of training image to a sub-area[28], and increased the constraint of position on depositional pattern to meet the requirement of local stability.
1.1. Method of reconstructing 3D model with 2D cross-section
1.1.1. Probability fusion
In mathematical statistics, many researchers have studied the method of probability fusion of 2D orthogonal cross-sections into 3D probability. Allard et al. divided the probability fusion mechanism into two: addition-based fusion and multiplication-based fusion[30]. As adjacent cross-sections in the same direction are similar in pattern, two independent parallel sections are fused by the addition formula of linear pooling, while the probabilities of sections in different directions are fused with multiplication formula of log-linear pooling to reflect anisotropy. For a point to be estimated, there are slices in m (1≤m≤3) directions and n (1≤n≤2) adjacent sections in each direction. For instance, the point X to be estimated in Fig. 1, first get conditional data events in a certain direction, scan the adjacent training images in this direction to acquire the matching data events, update the conditional probability density function of this point, and then obtain the fusion probability in this direction via the addition formula, as shown by equation (1).
where ${{\omega }_{i,j}}=\frac{{{l}_{i,j}}}{\sum\limits_{j=1}^{n}{{{l}_{i,j}}}}$
After getting the fusion probability in the corresponding direction, fuse the conditional probabilities in all orthogonal directions by multiplication formula to get the final conditional probability density function, as equation (2).
In equation (2), P0[Z(X)] is a priori probability. When $\sum\limits_{i=1}^{m}{{{w}_{i}}}=1$, the distribution of priori probability has no impact on the probability aggregation. The weight values in different directions can be the same or different. In practical application, the weighting of inverse distance is taken as the basis of its value, and the formula is as follows:
where ${{L}_{i}}=\text{min}\left( {{l}_{i,1}},{{l}_{i,2}},\cdots ,{{l}_{i,n}} \right)$
Fig. 1.
Fig. 1.
Schematic diagram of the distances between the point to be estimated and the cross-sections.
1.1.2. 2D conditional probability
In s2Dcd method, when estimating an unknown point, search the adjacent training image cross-sections in three directions, and integrate the two-dimensional probabilities in different directions to form three-dimensional conditional probabilities by means of probability fusion. The method of calculating the conditional probabilities on two-dimensional slices is consistent with the SNESIM method of multi-point statistics. For any direction, first get the conditional data points in this direction through the two-dimensional data template, that is, the two-dimensional data events; then, scan the 2D training images in the same direction, determine the matching data pattern, and count the number of repetition times of different data events at the point to be estimated, i.e. the number of occurrence times Ri,j(Zk) of different sedimentary facies Zk, and use the repetition frequency of data events to approximate the 2D conditional probability of the point to be estimated, namely:
1.1.3. Local search and pattern distance
In s2Dcd method, as every scan is to search the whole cross-section, it is possible to copy the pattern far away from the point to be estimated. These patterns are only restricted by a few conditional points, and thus may be different from local features. Chen et al. came up with a local search strategy[28]. As shown in Fig. 2, six cross-sections in 3 directions divide the space into 27 sub-areas, with 2 cross-sections in each direction. Each sub-area is surrounded by N sub-sections (3≤N≤6), and some sub-areas may not be closed. For any point to be estimated in a sub-area, the statistical information is only gained from the N sub-sections surrounding the sub-area in the search pattern. The local search strategy ensures the close distance between the sampled pattern and the point to be estimated, so the statistical information is more reasonable and credible. Apart from that, the statistical information comes from local part, which is similar to the search range of correlation of reservoir for variogram in two-point geological modeling, so the local search strategy also takes into account the statistical stationarity assumption.
Fig. 2.
Fig. 2.
Schematic diagram of spatial segmentation of local search strategy (revised from Reference [28]).
Taking into account that local slicing may result in low repetition rate of data events and unstable probability function, and thus increase the uncertainty of random sampling, Chen et al.[28] used the pattern distance threshold to get more data events and more stable conditional probabilities. The pattern distance d is usually adopted to characterize the similarity between conditional data events and models in training images. The smaller the pattern distance, the higher the similarity. For a complex reservoir, there are few data events in perfect matched pattern. Thus, in practical application, the minimum pattern distance threshold t is set in most cases. When d<t, the pattern is considered to be matched, and then the probability density function at the point to be estimated is updated. The pattern distance at the point to be estimated can be expressed as:
where ${{a}_{e}}=\left\{ \begin{align} & 0\quad Z\left( {{X}_{e}} \right)=Z\left( {{Y}_{e}} \right) \\ & \text{1}\quad Z\left( {{X}_{e}} \right)\ne Z\left( {{Y}_{e}} \right) \\ \end{align} \right.$
1.2. Improvement and testing of the method
1.2.1. Simulation based on adaptive spatial sampling
The research shows that although the local search strategy increases the constraint of sedimentary location and gives equal consideration to the non-stationary characteristics of reservoir, the simulation results are smoother and the reservoir from simulation has little variation. The reason is that the closer the distance, the smaller the variation of the sedimentary characteristics of local slice is; the similar sedimentary patterns result in high repeatability of a few data events, while the repeatability of data events reflecting local variation decreases, and finally obtained non-representative fusion probability distribution. In the course of simulation, the random sampling decreases in confidence and can’t reflect the variation of local reservoir, so the accuracy of simulation results is low. The essence is that it is difficult to estimate the posterior conditional probability distribution for conditional simulation with a small amount of data.
In seismic inversion, to acquire the posterior probability distribution of actual variables, ISR (Iterative Spatial Resampling) method of multi-simulation and multi- sampling is often used to achieve the stationarity of statistical sampling, i.e., stationary Markov chain, and it is taken as posterior probability distribution to guide the prediction of reservoir with seismic data. Mariethoz et al.[31] put forward an optimized ISR method, in which the data in the previous simulation results are re-sampled as new condition points to enhance the accuracy of the next simulation. But in ISR method, the data points sampled from the simulation results are random. If the sampling points themselves have large errors, the later iterative simulation with the sampling points as constraint conditions would have deviations inevitably, the iterative sampling would take longer time, and even result in local optimum but iterative inversion failure. To address this issue, Jeong et al.[29] put forward ASR (Adaptive Spatial Resampling) method, which does not carry out random resampling, but directly samples in areas with small errors and re-simulates areas with large errors. Practice proves that this method not merely accelerates the inversion process, but enhances the accuracy of prediction results.
In seismic inversion, the method of retaining points with smaller errors to increase conditional data to constrain and guide inversion has achieved fairly good effect. This idea can be borrowed to form a multi-point geostatistical simulation method based on adaptive spatial sampling. Before simulation, the end threshold of iteration is set, which can be the proportion of target lithofacies or the number of iterations. At the beginning of iteration, some points are sampled from the confidence region in the previous simulation results as additional conditional data in this iteration, to achieve the purpose of iterative re-sampling. Confidence region is defined as a point set with small pattern distance and significant pattern fusion probability, and significant pattern fusion probability means that a certain lithofacies has a high proportion of fusion probability among all types of lithofacies. Taking any point as an example, its pattern distance is d, its fusion probability is Pf, and the number of candidate facies is r, then the confidence region of the point can be expressed as:
The above formula means that in the simulation result, a point with a pattern distance of less than 5% and a fusion probability of one lithofacies of greater than 75% is regarded with the confidence of 1, otherwise the point is 0 in confidence. All the point sets with the confidence of 1 are regarded as confidence regions and are retained as conditional data to constrain and guide the next iteration statistics. Certainly, in consideration of different geological conditions, the definition standard of confidence region can be adjusted based on actual needs.
1.2.2. Simulation process
After adding adaptive spatial sampling to the local search method, the simulation steps of the new method are as follows: (1) determine simulation parameters such as the maximum search radius, maximum number of conditional points, iteration termination threshold and upper limit of iteration sampling data, etc.; (2) acquire conditional data events in all directions at simulation points, search matched patterns in sub-sections in corresponding directions, and update probability density functions in all directions based on pattern distances; (3) if there are two adjacent sub-sections in the same direction of the simulation point, then the fusion probability in this direction is gained by the linear pooling addition formula, then the fusion probability in all directions is obtained by the logarithmic pooling multiplication formula, and finally the simulation value of this position is determined; (4) if all nodes are simulated, skip to step (5), otherwise, turn to the next node and skip to step (2); (5) judge whether the simulation result is within the iteration termination threshold, if so, skip to step (6), otherwise, add some data points sampled from the confidence region in the previous simulation result to the original condition points, and skip to step (2); (6) get the final simulation results. Fig. 3 is the flow chart of the new method.
Fig. 3.
Fig. 3.
Flow chart of the new method.
1.2.3. Testing of the method
The study target stratum is meandering river deposition influenced by tides, and the lateral accumulation layers in point dams are well developed. Accurate prediction of lateral accumulation layer distribution is of crucial significance to oil reservoir development. Thus, the conceptual model of lateral accumulation layer is designed to test the algorithm. The grid number of the model is 90×74×100. In the model, the number of lateral accumulation layer strips is large, the vertical changes are fast, there are multiple lateral accumulation layer directions, the pattern structure is complex, with certain unstable characteristics (Fig. 4). A total of 11 sections (3 sections in xy direction, 4 sections in xz direction and 5 sections in yz direction) are taken as 2D training images on the 3D model, and the original local search method and the improved new method are compared and tested respectively.
Fig. 4.
Fig. 4.
Slices of training images.
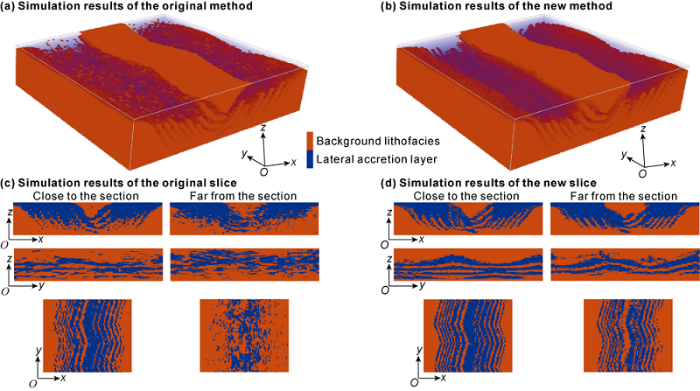
The same search strategy is adopted, with search radius set at 10, scanning ratio at 0.8, and upper limit of the number of conditional points at 70. In iterative sampling, the number of iterations is set at 2, and the standard of confidence region is that the pattern distance is less than 3%, the fusion probability is greater than 80%, and the sampling point data takes up 30% of the confidence region. The model is re-built by two methods, and the simulation results are shown in Fig. 5. The simulation results from the original method have the lateral accretion layers reproduced well near the corss-sections but gradually blurring away from the cross-sections (Fig. 5c). The reason is that when far away from the corss-sections, there are few conditional data of the lateral accretion layers, the condition data of river channels takes a high proportion, the models to be selected that accurately reflect the overlapping pattern take a small proportion, while other models to be selected that meet the conditions are large in number, which ultimately results in poor reproduction of the pattern. In the new method, simulation points with high confidence are retained as conditional data, which increases the amount of data information and enhances the identifiability of the pattern. The 3D probability distribution constructed by the new method is clearer. Thus, the sampling is more reasonable, and the pattern of the lateral accumulation layer can still be reproduced at a position far away from the section (Fig. 5d), which suggests that the method based on adaptive spatial sampling enhances the simulation accuracy and can be applied for practical modeling.
Fig. 5.
Fig. 5.
Comparison of simulation results by the two methods.
2. Geological characteristics of the research area
2.1. Overview of the area
The research area is situated in Alberta, Canada, and the oil sand reservoir of McMurray Formation was formed in the Early Cretaceous, and belongs to meandering river deposits influenced by tides in the estuary background[32,33]. The research area of about 12 km2 has 78 data wells in total, including 67 cored wells. Influenced by tides, the river water rises in level during the flood tide. During the ebb tide, the river water drops in level, accelerates in flow velocity and becomes shallower, resulting in extensive erosion and mud conglomerate and bottom conglomerate. During flat tide, the river flow velocity is slow and is only affected by the tide, leading to development of lateral accretion layers. But unlike the normal meandering river, the tide would still carry a small amount of sandy materials, so the lateral accretion layers formed are not pure mudstone, but interbedded silty mudstone and argillaceous siltstone alternating in high frequency. Meanwhile, the sand bodies intersect with each other due to the migration and swing of river channels, resulting in complex internal structure of the reservoir, which will seriously affect the later development effect.
2.2. Dissection of the reservoir
Based on the information of sand body distribution, variations of stratum thickness, lithofacies transition, plane distribution of dip and so on, the distribution of point bars in the meandering river is determined. Guided by Miall's order classification scheme[34], the fifth-order structural interface in the research area is defined as a single river channel interface, with scouring surface at the bottom. A thick layer of mudstone conglomerate with poor sorting and roundness on the scouring surface, gradually transits upward to relatively pure coarse sandstone and lateral accretion layer section, with occasional argillaceous deposit at the top, reflecting gradual weakening of hydrodynamic force. This set of deposit appears as bell or box shape on GR (natural gamma) and SP (natural potential) curves. The fourth-order interface is the point-bar interface in the river channel unit, which takes on bell shape on GR and SP curves. The third-order interface corresponds to the lateral accretion layer in the point bar, with high GR curve value and obvious return. Due to the double influences of water flow and tide, lateral accretion layers develop frequently and with thin thickness, which is the main factor affecting the development of oil sand. With reference to the investigation of outcrop near the research area[35,36,37], combined with the rich coring data, dip logging and lithologic combination characteristics of the research area, four kinds of point bar identification marks, namely, logging shape, rock facies change, dip combination change and sand body thickness distribution, have been set up, thus realizing the characterization of point bars. On this basis, according to the mudstone position interpreted by logging and the shale layer dip direction observed on the core, the extension direction of lateral accumulation layer is determined, and then the fine characterization of lateral accumulation layer is completed combined with the scale statistics of existing outcrop data (Fig. 6), and accurate characterization data of lateral accumulation layer is gained (Table 1), which lays a foundation for the establishment of training images.
Fig. 6.
Fig. 6.
Fine dissection of lateral accretion layers in point bar.
Table 1 Characteristic parameters of lateral accretion layers in each sublayer.
| No. of sublayer | Thickness/m | Lateral span/m | Extension/m | Dip angle/(°) | ||||
|---|---|---|---|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | Maximum | Minimum | |
| asm4 | 4.30 | 0.10 | 2592.76 | 749.13 | 665.58 | 186.34 | 6.5 | 2.6 |
| asm3-2 | 2.86 | 0.12 | 1001.71 | 335.78 | 532.27 | 196.37 | 7.6 | 2.4 |
| asm3-1 | 3.83 | 0.13 | 1224.13 | 297.64 | 198.30 | 82.90 | 7.8 | 2.0 |
| asm2 | 1.26 | 0.15 | 1316.70 | 219.00 | 169.16 | 72.84 | 7.8 | 2.1 |
3. Modeling of sedimentary facies
The lateral accumulation layer in the research area has multiple tendencies and the dip angle varies extensively, so the modeling of such lateral accumulation layer is not easy to be realized by the traditional geostatistical method. Despite that the multi-point geostatistical method has been successfully applied in characterizing lateral accumulation layers[38], it is a difficult point to build a 3D training image conforming to underground characteristics. In this thesis, in the idea of hierarchical modeling[38,39,40,41], the model of muddy lateral accumulation layer is built first by a new method, and then the modeling of sedimentary facies is completed on the basis of the lateral accumulation layer model. Considering comprehensively the thickness and average well spacing of lateral accumulation layers in the research area, it is determined that the step size of plane grids in the research area is 20 m×20 m, the longitudinal thickness of grids is 0.2 m, and the number of grids is 174×251×262.
3.1. Establishment of 2D training images
The 2D training images are derived from all sorts of transverse and longitudinal cross-sections and 2D plane sedimentary facies maps in geological analysis. Limited by the requirement of probability fusion in the algorithm, the slices must intersect vertically, so the 2D training images used must be orthogonal. But the geological well logs aren’t necessarily orthogonal, so it is essential to adjust the position of training image of vertical cross-section in consideration of the actual situation. Based on the idea of hierarchical modeling, the first layer focuses on the characterization of lateral accretion layer, so lateral accretion layer is taken as the characterization object, and other facies are taken as the background. Fig. 7 shows the digitizing results of a well log, which is approximately parallel with the cross-section of training image (Fig. 8). The possible shapes of lateral accretion layers at the position of training image are deduced based on the extension characteristics of the lateral accretion layers on the well logs. In addition, since the well logs do not run through the research area, it is necessary to complete the cross-section of training image, which can be inferred with reference to the results of plane interpretation and experience. Of course, the case that the cross-section of training image and the well logs are in an oblique state is inevitable, it is required to project the interpretation results of the well logs onto the cross-section of training image to determine its pattern form on the training image.
Fig. 7.
Fig. 7.
Interpretation of lateral accretion layers on the well logs and cross-section of digital training image.
Fig. 8.
Fig. 8.
Sedimentary facies map of asm4 sublayer (a) and digital slice training image (b).
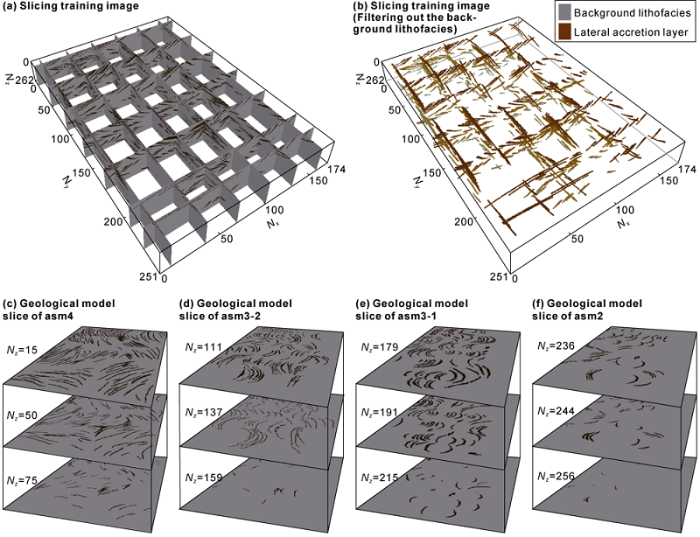
For horizontal slices, 3 horizontal slices (top, middle and bottom) are generally taken in each sublayer to reflect the vertical variations. The idea of establishing the horizontal slices is consistent with that of conventional research on sedimentary microfacies. Taking asm4 sublayer as an example, the training images of horizontal slices are based on sedimentary facies map (Fig. 8a). Firstly, the well point data on the slices of this layer and the section training image data established before are obtained; then, the lithofacies data of each well in the sublayer is divided based on the position of slice, and the dominant facies information of well point at horizontal slice is obtained; finally, combining with the quantitative parameters such as width, radian, extension length and interval distance of the lateral mass gained in the configuration dissection in the horizontal direction, the extension form of the lateral mass at known points on the slice is finally determined, and the training image of horizontal slices is established (Fig. 8b)
In consideration to the characteristics of the research area, the training images of 7 EW slices and 6 NS slices are built (Fig. 9a, 9b). Most of the slices pass through the target geological body and can reflect the crpss-section shapes of lateral accretion layers, including the changes in inclination and thickness. The horizontal slices of each sublayer reflect the vertical gradual changes of lateral accretion layers on the basis of the sedimentary facies map, with dense lateral accretion layers at the top and less and less toward the bottom (Fig. 9c-9f).
Fig. 9.
Fig. 9.
2D training image.
3.2. Modeling of lateral accretion layers
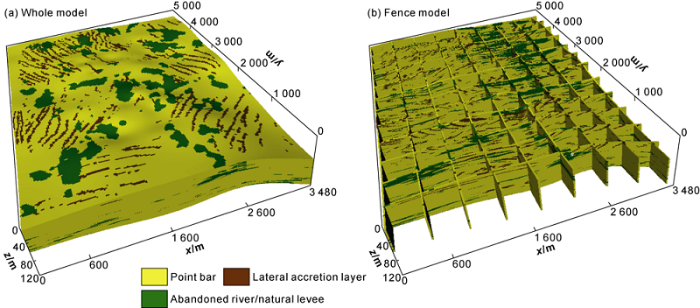
As the muddy lateral accretion layers are characterized by narrow width, thin thickness and long lateral extension, once the search range is too large, the ratio of the lateral accretion layer to the background facies will decrease significantly within a template range. Finally, the search radius is 3×3×3, the upper limit of the number of conditional points is 80, and the scanning ratio of sub-section is 80%. The standard of confidence region is that the pattern distance is less than 5%, the fusion probability is greater than 75%, the sampling point data takes up 35% of the confidence region, and the iteration termination condition is that the lateral accretion layer accounts for more than 6%. It is worth noting that the 2D cross-section in simulation is both training image and conditional data. Under this parameter setting, a new method is applied to simulate the lateral accretion layers of each sublayer, and the obtained model is shown in Fig. 10, with the lateral accretion layer accounting for 6.5%. From the cross-section (Fig. 10b), the lateral accretion layers have good continuity, and are similar in shape to geological dissection, and gradually become thinner from top to bottom, and in the same point bar, the lateral accretion layers are basically consistent in dip. From the plane (Fig. 10c), the lateral accretion layers have obvious zoning features, and the closer to the training image, the better the model reproduces. The model can reflect the vertical change of lateral accretion layers, and the lateral accretion layers decrease gradually from top to bottom in a sublayer. This suggests that the new method works well in multi-directional modeling of lateral accretion layers, and reflect the non-stationary characteristics of lateral accretion layers from top to bottom.
Fig. 10.
Fig. 10.
Model of lateral accretion layers.
3.3. Validation of the lateral accretion layer model
3.3.1. Validation with wells not participating the model building
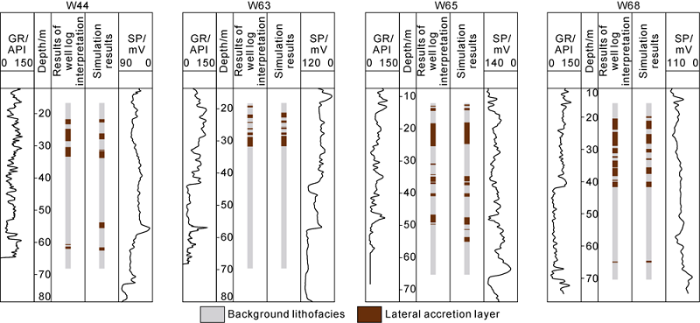
Two cross-sections are selected in the research area, and two wells on each cross-section are not involved in the model building of lateral accretion layers in the research area; the lateral accretion layer model is built with the remaining wells to predict the lateral accretion layers at the wells not included in the model building to test the accuracy of the model. Statistics show that the new method can accurately predict the distribution of lateral accretion layers, and the lateral accretion layers at the removed wells (W44, W63, W65 and W68) are basically reproduced (Fig. 11). Comparing the prediction results of lateral accretion layers at the four wells with the original interpretation results shows the prediction errors of the ratio of lithofacies at the four wells are -12.10%, 4.45%, 4.44%, and -16.91% respectively, and the average accuracy of lithofacies prediction at the wells is 90.5% (Table 2). Further, the prediction results are carefully compared point by point and grid by grid, and the average prediction accuracy at the four wells is as high as 88.8%. Without considering the background lithofacies, the lateral accretion layers in the target stratum are compared point by point with a correct ratio of 74.5%. Clearly, the new method can not only accurately reflect the proportion of sedimentary facies, but accurately predict the spatial positions of lateral accretion layers and reveal the structure of reservoir, showing strong prediction capability.
Fig. 11.
Fig. 11.
Validation with wells removed from model building.
Table 2 Prediction of lateral accretion layers in removed wells.
| Well | Point-to-point correct ratio (target interval)/% | Correct ratio of lateral accretion layer prediction/% | Cumulative thickness of lateral accretion layers | ||
|---|---|---|---|---|---|
| Interpretation/m | Predicted/m | Error/% | |||
| W44 | 87.21 | 73.33 | 9.42 | 8.28 | -12.10 |
| W63 | 92.37 | 78.91 | 6.29 | 6.57 | 4.45 |
| W65 | 88.55 | 76.52 | 14.63 | 15.28 | 4.44 |
| W68 | 87.02 | 69.04 | 16.68 | 13.86 | -16.91 |
3.3.2. Validation with horizontal wells
Two new horizontal wells (PW1 and PW2) were drilled in the research area lately, and the drilling results of the two horizontal wells are compared with prediction results from the simulation to verify the accuracy of the model. Fig. 12 shows the projections of the lateral accretion layer model on the trajectory plane of the two wells based on their trajectories, which are compared with the sandstone and mudstone layers interpreted by horizontal well logging. On the whole, the lateral accretion layers obtained by simulation can basically match with the logging interpretation results. Horizontal well PW1 cuts through a point bar, and is perpendicular to the flow direction of river channel. The cross-section shows obvious lateral accretion. Based on the law from geologic understandings, three lateral accretion layers are interpreted on the cross-sections of two vertical wells (W43, W44) near PW1. In the simulation results, the lateral accretion layers near the wells are reproduced better and can match with the horizontal well, but those between the wells in local parts haven’t been reproduced. The horizontal well PW2 is consistent with the flow direction of the river channel, and the cross-section shows the upward convex shape of lateral accretion layer. The approximate position of lateral accretion layer in the simulation results is consistent with that of the horizontal well. Comparing with the interpretation results of lateral accretion layers in the two horizontal wells point by point shows, the prediction results have an accuracy rate up to 80%. The horizontal sections of wells in the research area are all in asm3-1 and asm2 sublayers at the bottom of the target stratum. Due to strong hydrodynamic force, the lateral accretion layers in these sublayers are poorly remained and strong in randomness. But the validation results of the horizontal wells suggest that the prediction results of the new method accurately reflect the distribution characteristics of lateral accretion layers, and the models have fairly high accuracy.
Fig. 12.
Fig. 12.
Comparison of interpretation results of horizontal wells with models.
3.4. Sedimentary facies model
On the basis of lateral accretion layer model, the sequential simulation method is applied to conduct the 2nd-level modeling to simulate other geological masses in the background facies. Based on the well point condition data and the large-scale distribution of geological masses, the variogram model of different sedimentary facies in each sublayer is set up, and the distribution of point bars (sandstone and conglomerate), natural dikes and abandoned river channels is predicted by using the constraint of vertical probability distribution (Fig. 13), which provides the facies model constraint for physical property distribution and calculation of reserves.
Fig. 13.
Fig. 13.
Sedimentary facies model.
3.5. Calculation of reserves
The scale of reserves is the comprehensive performance of porosity, water saturation, net-gross ratio and other parameters, and the accuracy of reserve calculation can be taken as the standard to test geological model and physical property model. On the basis of geological model, the effective porosity model and water saturation model of the research area are built by means of simulation of facies controlled sequential indicators. The effective porosity in the research area is concentrated between 20% and 35%, and the water saturation covers a wide range from 10% to 100%. Based on the coverage of 5 development well groups in the research area, 5 blocks are divided; the average physical properties and reserves of different blocks in the model are calculated and compared with the average physical properties and predicted reserves of well groups (Table 3). The error of reserves is less than 10%, indicating that the geological model has relatively high accuracy.
Table 3 Statistics on reserves of the development blocks.
| Block | Porosity | Water saturation | Reserves | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Well group/% | Model/% | Error/% | Well group/% | Model/% | Error/% | Well group/104 m3 | Model/104 m3 | Error/% | |
| A | 31 | 28.40 | -8.4 | 34.9 | 32.20 | -7.7 | 177.44 | 165.6 | -6.7 |
| B | 31 | 27.44 | -11.5 | 30.6 | 33.36 | 9.0 | 314.88 | 293.7 | -6.7 |
| C | 29 | 25.65 | -11.6 | 29.0 | 26.28 | -9.4 | 216.76 | 197.2 | -9.0 |
| D | 27 | 25.64 | -5.0 | 39.0 | 39.28 | 0.7 | 290.53 | 293.2 | 0.9 |
| E | 33 | 31.31 | -5.1 | 25.0 | 32.16 | 28.6 | 221.42 | 201.3 | -9.1 |
3.6. Verification with dynamic data
The geological model is verified by numerical simulation, a horizontal development well group (Block D) is selected, and the grid of the geological model is adjusted to 2 m×50 m×1 m, the data of productivity of well groups and wellhead pressure are fitted historically, and the difference between simulated data and actual production data is compared, the model is adjusted accordingly and the fitting effect is analyzed as well. Statistics show that out of the 6 oil production wells in Block D, the fitting errors of 5 wells are less than 5%, suggesting that the geological model has relatively high confidence.
4. Conclusions
In this thesis, a multi-point geostatistical simulation method based on adaptive spatial sampling to re-build a 3D model from 2D cross-sections is presented. In this method, the sampling points with high confidence in the previous simulation are taken as additional conditional points in the present simulation to eliminate the poor simulation effect resulting from the scarcity of well point data in the traditional modeling method; meanwhile, transforming geological sections into training images and building 3D geological models can avoid the dependence of traditional multi-point geostatistics method on 3D training image. In the modeling of actual blocks, for the narrow and thin lateral accretion layers, this method can also well reproduce the spatial form of lateral accretion layers. Validation with wells not participating the simulation shows a correct ratio of over 85%, and the coincidence rates between results of log interpretation and prediction of lateral accretion layers reach up to 80%.
This method needs to be further perfected in three aspects. (1) Since the positions of slices have a strong impact on the simulation results, once the adjacent slices do not pass through the target geological mass, it is hard to reflect the shape of the target, and the slice density needs to be increased. In practical application, it is required to select appropriate locations to build 2D cross-section training images in line with the overall characteristics of the research area. With regard to selecting the number of slices, analyzing the scale and variability of the reservoir is a good approach. For areas with large scale and small variability, a small number of slices can be used, on the contrary, more slices are needed. (2) Currently, the 2D slice training images used must be orthogonal, so the interpretation results of well logs can’t be directly digitized into training images, and projection conversion is needed, the accuracy of which will inevitably affect the prediction results of the model. (3) The method of adaptive iterative sampling comes from seismic inversion, which can effectively make use of the original seismic records, and select areas with small errors by comparing with synthetic seismic records. In this method, as there is no target reference, the significance of pattern probability and pattern distance are used as standards for screening. Although the simulation results with high sampling probability are more likely to be saved, local special events may be lost, which could affect the accuracy of the model. It is a vital research direction to make use of seismic record constraints in the simulation in the future.
Nomenclature
C—confidence area;
d—pattern distance;
e—the sequence number of the conditional data point in the pattern;
i—serial number in the slice direction;
j—serial number of adjacent cross-section in the same direction;
k—serial number of facies;
l—distance from the point to be estimated to the adjacent parallel cross-section;
L—the minimum distance from the point to be estimated to the adjacent parallel cross-section;
m—number of section directions;
n—the number of adjacent sections in the same direction;
N—number of sub-sections;
Nx, Ny, Nz—grid numbers in x, y, z directions;
P—pattern probability of adjacent parallel cross-sections;
P0—prior probability;
Pf—fusion probability of the point to be estimated;
Pi,j—probability of occurrence of a facies in the j-th cross- section in the i-th direction;
Pt—fusion probability of adjacent parallel cross-sections;
q—the number of conditional data points in the pattern;
r—number of candidate facies;
Ri,j—the occurrence times of a facies in the j-th cross-section in the i-th direction;
t—acceptance threshold of pattern distance;
v—number of facies types;
w—fusion weights of cross-sections in different directions;
x, y, z—rectangular coordinate system, m;
X, Y—points to be estimated;
Zk—facies type at the point to be estimated;
Z(X)—pattern value at point X to be estimated;
ω—fusion weight of adjacent parallel cross-sections.
Reference
Conditional simulation of complex geological structures using multiple-point statistics
The progress of reservoir stochastic modeling
Research achievements on reservoir geological modeling of China in the past two decades
Progress and prospect of multiple-point geostatistics
Preliminary study on a depositional interface-based reservoir modeling method
Perspective of development in detailed reservoir description
A pattern-based multiple point geostatistics method
Stochastic modeling for characteristics of petroleum reservoir constrained by facies
A review of development course and prospect of petroleum reservoir characterization and stochastic modeling
Sequential simulation with patterns
Filter-based classification of training image patterns for spatial simulation
Stochastic simulation of patterns using distance-based pattern modeling
Reconstruction of incomplete data sets or images using direct sampling
A training image evaluation and selection method based on minimum data event distance for multiple-point geostatistics
A training image optimization method in multiple-point geostatistics and its application in geological modeling
A training image optimal selecting method based on composite correlation coefficient ranking for multiple-point geostatistics
Improving the accuracy of geological model by using seismic forward and inversion techniques
Generation and application of three-dimensional MPS training images based on shallow seismic data
Regionalized multiple-point stochastic geological modeling: A case from braided delta sedimentary reservoirs in Qaidam Basin, NW China
Application of multi-point geostatistics in deep-water turbidity channel simulation: A case study of Plutonio oilfield in Angola
Establishment of training images of turbidity channels in deep waters and application of multi-point geostatistical modeling
Prediction of permeability for porous media reconstructed using multiple-point statistics
Pore space reconstruction of vuggy carbonates using microtomography and multiple-point statistics
Research on the reconstruction method of porous media using multiple-point geostatistics
3D multiple-point statistics simulation using 2D training images
Digital core modeling based on multiple-point statistics
Review of digital core modeling methods
Locality-based 3-D multiple-point statistics reconstruction using 2-D geological cross-sections
A fast approximation for seismic inverse modeling: Adaptive spatial resampling
Probability aggregation methods in geoscience
Bayesian inverse problem and optimization with iterative spatial resampling
Architectural analysis of compound point-bar sandbody in inner estuary of the Lower Cretaceous McMurray Formation in Kinosis area, Athabasca, Canada
Fine dissection of meandering river point bars based on shallow seismic data: A case study of Mcmurray reservoir in a block, Canada
Architectural-element analysis: A new method of facies analysis applied to fluvial deposits
DOI:10.1016/0012-8252(85)90001-7 URL [Cited within: 1]
Differential entrapment of charged oil: New insights on McMurray Formation oil trapping mechanisms
DOI:10.1016/j.marpetgeo.2012.05.004
URL
[Cited within: 1]

The Lower Cretaceous McMurray Formation is the primary host of the Athabasca oil sands deposit, one of the largest petroleum deposits in the world. Regional studies show that within the McMurray Formation, bitumen-saturated reservoir sands are encountered within the western, central and northeastern sections of the northeastern Athabasca deposit, while the southeastern part of the deposit has never been charged by petroleum, and that, the lateral contact between petroleum- and water-saturated reservoir sands is in some instances characterized by rapid changes in bitumen saturation, even between closely spaced wells. In the literature, a number of petroleum entrapment schemes have been proposed to explain how the bitumen accumulated through different trapping mechanisms, however controversy remains.
This paper investigates the concept of inter-compartmental petroleum "fill and spill" charge and entrapment in a setting where compartments are clearly defined by mud-filled channel deposits. Classical molecular maturity parameters based on gas chromatography - mass spectrometric analysis of hydrocarbon compounds that are extracted from the bitumen show notable changes in composition between the geologically defined reservoir compartments. Relatively higher maturity sourced oil resides in the western compartment while maturity decreases to the eastern most compartment suggesting that the eastern compartment was filled by petroleum of lower maturity which has been displaced via fill and spill as petroleum migration from an increasing maturity source enters compartments to the west. Oil saturation and hydrocarbon geochemistry results also suggest the oil charge was very limited locally and individual compartments located towards the eastern edge of the Athabasca may not have seen the multiple charges evident in the oil sands to the west.
The concept of inter-compartmental fill-and-spill provides new insights regarding the often over-looked intra-formational geological controls on reservoir charge in the McMurray Formation. The concept explains that apparently sharp lateral oil-water contacts are in fact due to mud-filled channel deposits which at least locally serve as lateral seals. This concept should be applicable to other meandering fluvial belt reservoirs worldwide and suggests a necessity to revise existing stratigraphic trap schemes by including the point bar stratigraphic play type of trap as one of the trapping mechanisms. Additionally, geochemical gradients can be used as a tool for defining the presence and extent of individual compartments as well as the level of fluid communication as an aid to well placements. (c) 2012 Elsevier Ltd.
Reservoir characterization and multiscale heterogeneity modeling of inclined heterolithic strata for bitumen-production forecasting, McMurray Formation, Corner, Alberta, Canada
DOI:10.1016/j.marpetgeo.2017.02.003 URL [Cited within: 1]
Unsuccessful cut offs - origin and partial preservation of enigmatic channel fills encased within a large-scale point-bar deposit: The McMurray Formation type section, Alberta, Canada: GHINASSI M, COLOMBERA L, MOUNTNEY N P, et al. Fluvial meanders and their sedimentary products in the rock record
A new stochastic modeling method for 3-D forecasting lateral accretion beddings of point bars in meandering rivers
Hierarchy analysis in reservoir researches
Hierarchical modeling method and its application in the construction of fluvial architectural elements model
3-D Hierarchical modeling of the braided channel reservoir of Saertu oilfield