Introduction
After more than ten years of exploration, shale oil reservoirs in multiple formations and multiple areas of China have made breakthroughs in the production, making shale oil a significant replacement for conventional oil and gas[1]. Drawing on the experiences of large oil and gas fields abroad, oil and gas developers in China have carried out technology exploration and field trials about volume fracturing and achieved a prosperous production[2]. However, continental shale oil reservoirs usually have multiple layers uneven in thickness and weak surfaces between the layers, which are difficult to penetrate by hydraulic fractures (HFs), so it is difficult to realize large-scale and high-efficiency development. Cross-layer fracturing is an efficient way to connect multiple production layers in shale oil reservoirs and enhance the utility of the oil resource in thin interbed.
Many scholars in China and abroad have studied cross-layer fracturing. Shale oil reservoirs often have rock layers of different lithologies stacking over each other and natural structural planes like muddy lamina of sandstone and shale bedding etc. Hence, it is important to find out the communication rules between HFs and natural structural planes to realize cross-layer fracturing[3,4,5,6,7]. Previous researchers have studied cross-layer fracturing in multi-lithologic combination strata, put forward the evaluation system of cross-layer fracturing effect of shale gas reservoirs, and established the HF height control method of shale gas reservoir[8,9,10,11,12,13,14,15,16]. They found that horizontal stress difference, interface strength, and lamina thickness were the internal factors affecting the ability of HFs to penetrate natural fractures (NFs)[17,18,19,20,21,22,23,24], while the displacement and viscosity of fracturing fluid were the external factors affecting the interaction between HFs and NFs[25,26,27,28,29,30]. The previous studies focused on the fracture height control of shale and carbonate reser-voirs with single lithology but seldomly involved in the study of cross-layer fracturing of shale oil reservoirs with layers of multiple lithologies.
Shale oil was found in the Paleogene Sha-3 Formation in the Dongpu Sag, Bohai Bay Basin. However, the reservoir is tight, with low natural productivity, and the lacustrine shale reservoir has strong longitudinal heterogeneity, weak cementation planes between layers, and large horizontal stress difference[31,32,33]. The selecting of fracturing stratum and construction parameters is the key to realizing cross-layer fracturing of this section. Aiming at the volumetric fracturing in the shale oil reservoir in the Dongpu sag, this paper uses downhole cores to carry out physical simulation experiments of fracturing in different layers to find out the correlations between typical fracture patterns and construction parameters in shale oil reservoirs. Combining the numerical simulation method of embedding global cohesive elements, we analyze the propagation law of HFs through layers.
1. Physical simulation of hydraulic fracturing in shale oil reservoirs
1.1. Physical simulation
Well Pu 165 well is located in the south of Dongpu sag with a drilling depth of 3707 m, and the target horizon is the lower sub-member of the Sha-3 Formation. Six cores taken from the shale oil reservoir at a depth of 3400- 3660 m in well Pu 156 were taken for physical simulation experiments of hydraulic fracturing (Fig. 1). The 1# to 6# cores were taken from 3420, 3422, 3424, 3656, 3659, and 3663 m respectively, among which 3# to 6# cores meet the standard of favorable shale formation in TOC and Ro[34]. The 1# and 2# cores have no NFs, and only black banded thin interbeds with a thickness of 1-2 mm; the 3# core has obvious bedding with weak interlayer cementation; the 4# core and 6# core have no obvious NFs; the 5# core has a group of high angle NFs filled by calcite about 0.5 mm wide.
Fig. 1.
Fig. 1.
Photos of cores taken from the shale oil reservoir in the lower sub-member of Sha-3 Formation in Well Pu 156.
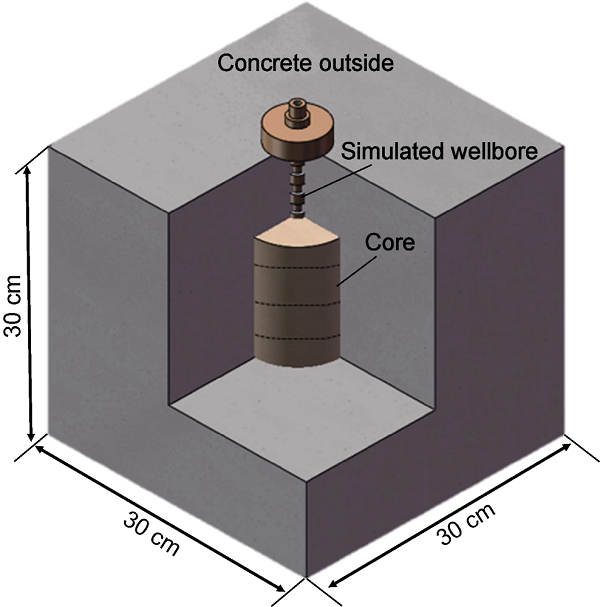
Each full diameter core was wrapped with concrete into a sample of 30 cm×30 cm× 30 cm. The core was kept in the middle of the sample during the pouring process (Fig. 2). After curing for 48 h, drilling down about 15 cm from the surface of each sample to the middle of the core, and then cementing with epoxy resin glue. Physical simulation experiments of hydraulic fracturing were carried out by a true triaxial fracturing system.
Fig. 2.
Fig. 2.
Schematic diagram of a full-diameter core of shale oil reservoir wrapped in concrete.
The Kessel experiments were carried out on samples having similar depths with 3# to 6# cores, and the experimental results are shown in Table 1. Took the averages of the two sets of Kessel experiment results, the indoor experimental three-dimensional stresses were calculated based on the similarity criterion[6]: the overburden stress of 38.3 MPa, the horizontal maximum principal stress of 37.1 MPa, and the horizontal minimum principal stress of 32.4 MPa. Through similar scale coefficients and similar criterion conditions composed of single-valued condition quantities[6], the displacement values of the true triaxial physical simulation experiments were determined to be 35 mm3/min (corresponding to the site displacement 4.5 m3/min) and 50 mm3/min (corresponding to the site displacement 6.7 m3/min). The viscosities of fracturing fluid were 3 mPa·s and 10 mPa·s, respectively. Applied overlying ground stress along the wellbore direction to simulate straight hole fracturing. A slickwater fracturing fluid system was used in the experiments, and the fluorescent agent was added for tracing. The experimental parameters and the types of HFs after fracturing are shown in Table 2.
Table 1 Ground stresses measured by Kessel experiments.
| Lithology | Depth/ m | Confining pressure/ MPa | Maximum horizontal principal stress/MPa | Minimum horizontal principal stress/MPa |
|---|---|---|---|---|
| Dark gray siltstone | 3655.3 | 36 | 76.46 | 65.63 |
| Light gray siltstone | 3661.5 | 36 | 77.80 | 65.63 |
Table 2 Experimental parameters and results of true triaxial fracturing on shale oil reservoir cores.
| Core No. | Displacement / (mm3·min-1) | Fracturing fluid viscosity/(mPa·s) | HFs shape after fracturing |
|---|---|---|---|
| 1# | 35 | 10 | Cross pattern |
| 2# | 35 | 3 | Cross pattern |
| 3# | 35 | 3 | Ladder pattern |
| 4# | 50 | 3 | Cross pattern |
| 5# | 35 | 3 | Straight line |
| 6# | 50 | 10 | Cross pattern |
1.2. Results and discussion
1.2.1. Typical HF patterns of shale oil reservoir cores
After the fracturing experiments, the cores in the cement samples were observed. It was found that the HFs in the cores were mainly divided into cross-pattern fractures, ladder fractures, straight-line fractures. The cores corresponding to the three fracture patterns, in turn, were sandstone without high-angle NFs, shale rock, and sandstone with high-angle NFs (Fig. 3). In the 2# purple siltstone core with 2 laminae (Fig. lb), the HFs started to develop in the direction of the maximum horizontal principal stress, penetrated the two laminae when growing longitudinally, and diverted at the second lamina, forming a cross pattern fracture. In the 3# dark gray shale with obvious horizontal bedding, the HFs started to develop in the direction of the maximum horizontal principal stress, were obstructed after penetrating two beddings longitudinally and turning to the third bedding, forming ladder fractures. Apparently, the longitudinal extension of HFs in the 3# shale core was restricted by beddings. In the 5# gray siltstone core with a group of high-angle NFs filled with calcite, the fracturing fluid leaked along the high-angle NFs, and the HF mainly spread along the high angle NFs, forming a straight line shape fracture.
Fig. 3.
Fig. 3.
The shapes of HFs under the influence of structural planes (red dashed lines represent structural planes, yellow dashed lines represent artificial fractures).
Different lithology and NF patterns caused differences in HFs in shale oil reservoirs. The HFs in the sandstone layer without NFs are cross-shaped, the HFs in the shale layer with obvious bedding are ladder-shaped, and the HFs in sandstone with NFs are straight-line shape. The HFs in the sandstone layer extend longitudinally in strips (such as 2# core). In contrast, the HFs in the shale layer are likely to propagate laterally induced by bedding (such as 3# core).
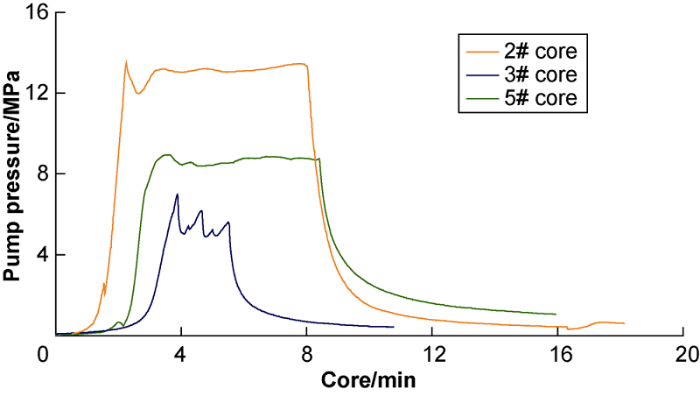
It can be seen from the pump pressure curves (Fig. 4) that: The 2# core is tight and the fracture initiation is difficult, and the fracture pressure is up to 13.7 MPa; the curve has an obvious fluctuation at 2.5 min, indicating the fracture growth was hindered by the lamina. The high-angle NFs in 5# core provided channels for fracturing fluid leak, and the fracture pressure reduced to 8.8 MPa; the pump pressure curve was flat after the fracture initiation, indicating that the extension process of the HF was not significantly hindered, and only one main fracture along the high-angle NF was formed. In the 3# core with weakly cemented bedding, the HFs were easy to initiate, and the fracture pressure was the smallest (7.1 MPa); the curve fluctuated at 4.8 min and 5.6 min, respectively, which corresponded to the obstruction of shale beddings twice during the longitudinal expansion of HFs. The fracture pressures decline successively in order of tight sandstone, fractured sandstone, and shale rock in shale oil reservoir of sub-member of Sha-3 Formation.
Fig. 4.
Fig. 4.
The influences of structural planes in different cores on the pump pressure curves.
1.2.2. The influence of fracturing fluid viscosity and displacement on HFs
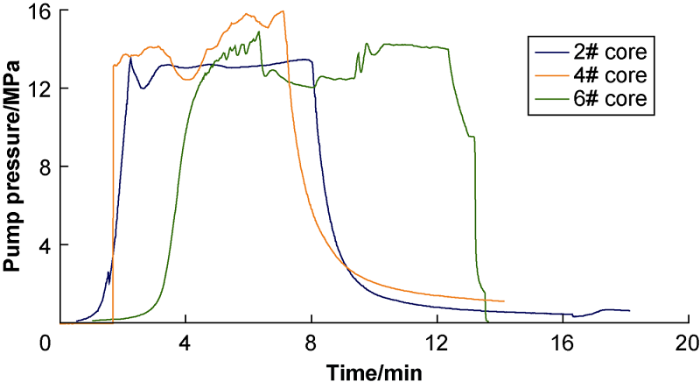
Due to the low permeability and strong heterogeneity of shale oil reservoirs, the viscosity and displacement of fracturing fluid would affect the shape of HFs. The 2# core and 4# core are both tight sandstone, and they were fractured at lower displacement (35 mm3/min) and higher displacement (50 mm3/min), respectively. The HFs in 2# core started to expand in the direction of the maximum principal stress, penetrated and opened a horizontal lamina, forming a cross-shaped fracture. The HFs in 4# core started to expand in two directions of the maximum principal stress and the minimum principal stress around the well; the main fracture in the direction of the maximum principal stress crossed and opened a lamina, forming 3 intersecting HFs (still regarded as cross-shaped fractures, but more complicated in shape in this paper). Compared with 2# core, the HFs in the 4# core are more complicated under the effect of larger displacement. From the pump pressure curves, the fracture pressure of the 4# core (13.8 MPa) is slightly higher than that of the 2# core (13.5 MPa) (Fig. 5). The curve of 2# core had a pressure buildup at 2.5 min, corresponding to the blocking of HFs propagation by the lamina. The 4# core pump pressure curve showed a significant decrease at 3.1 min and 5.9 min, corresponding to the process of HF initiation and communication with the horizontal lamina.
Fig. 5.
Fig. 5.
The influence of fracturing fluid parameters on the pump pressure curves.
The 4# core and 6# core were both tight sandstone, fractured with low viscosity (3 mPa·s) and high viscosity (10 mPa·s) slickwater, respectively. The HFs in the 6# core started to develop along the direction of the maximum principal stress and penetrated the lamina vertically to form cross-shaped fractures. Three intersecting HFs were formed in 4# core, and the shape of HFs was more complex (Fig. 6). It can be seen from the pump pressure curve that the fracture pressure of the 6# core was 14.5 MPa, and the pressure built up again at 9.2 min, correspondeding to the opening of the lamina by HFs.
Fig. 6.
Fig. 6.
HF morphology under the influences of different fracturing fluid parameters (red dotted line represents structural plane, yellow dotted line represents artificial fracture).
2. Numerical simulation of the cross-layer fracturing of shale oil reservoirs
Through true triaxial physical model experiments on cores from different shale oil layers, a preliminary understanding of fracture propagation laws in different reservoirs through vertical well fracturing was obtained and found that whether HFs penetrate the bedding determines the shape of the fracture. However, it is impossible to quantify the influence of factors such as interface strength on fracture height through laboratory experiments only. For this reason, this paper used a numerical simulation method to study the propagation of HFs in shale oil reservoirs with multi-lithologic layers stacking over each other.
2.1. Globally embedding cohesive element method
The software used in the numerical simulation is the 2017 version of ABAQUS, which uses the global embedding cohesive element method based on the finite element method. The cohesive model can simulate the separation of two interfaces at the crack tip and defines the plasticity and softening effects of the fracture tip in a semi-brittle material like shale. Compared with the linear elastic mechanical model, the cohesive model can get a more accurate fracture shape. This study adopted the globally embedding cohesive element method, in which the cohesive elements were embedded between the element grids in batches, and the fractures developed along the edges of the elements[35].
2.1.1. Cohesive element constitutive model
A linear elastic constitutive model based on the traction-separation law is used to describe the hydraulic fracture propagation, and the cohesive units satisfied the linear elastic relationship before damage:
2.1.2. Hydraulic fracture initiation criterion
The initiation of the fracture follows the maximum principal stress criterion, and it fails when the normal tensile stress or tangential stress reaches the maximum strength:
where $\left\{ \begin{array}{*{35}{l}} \left\langle {{\sigma }_{n}} \right\rangle =0\text{ }{{\sigma }_{n}}<0 \\ \left\langle {{\sigma }_{n}} \right\rangle ={{\sigma }_{n}}\text{ }{{\sigma }_{n}}\ge 0 \\\end{array} \right.$
2.1.3. Hydraulic fracture propagation criterion
The propagation of the fracture after initiation is based on the damage evolution criterion of effective displacement, and the damage variable D is defined:
2.2. Model parameters setting
According to the stratigraphic conditions in the study area, a pseudo-three-dimensional HF propagation model is established, with the model size of 10 m×5 m, and the longitudinal lithology combination is shown in Fig. 7a. The layer ①, layer ⑤, and layer ⑨ of sandstone were set as production layers. Also, a group of conjugate weak planes with high permeability was set in layer ⑨ to represent the NFs. The quadrilateral grid was adopted for local grid refinement in the fracture propagation area, and the grid unit size was 0.15 m×0.15 m (Fig. 7b). Mechanics parameters of sandstone and shale samples similar in depth with cores in the fracturing experiments above were measured by triaxial tests (Table 3). Three-dimensional ground stresses were set regarding the in-situ stress measurement results of Kaiser experiments (Table 1). To ensure the longitudinal extension of HFs, two initial damage units were set above and below the perforation point.
Fig. 7.
Fig. 7.
Schematic diagram of model grid division and lithology combination.
Table 3 Rock mechanic parameters of different core samples.
| No. | Elastic modulus/ GPa | Poisson's ratio | Compressive strength/MPa | Cohesion/MPa | Internal friction angle/(°) |
|---|---|---|---|---|---|
| Sandstone 1# | 32.03 | 0.280 | 261.73 | 25.14 | 38.65 |
| Sandstone 2# | 25.62 | 0.290 | 280.44 | ||
| Sandstone 3# | 24.87 | 0.270 | 267.74 | ||
| Mean | 27.50 | 0.280 | 269.97 | ||
| Shale 1# | 34.41 | 0.280 | 274.66 | 17.45 | 34.23 |
| Shale 2# | 21.26 | 0.290 | 261.81 | ||
| Shale 3# | 24.30 | 0.280 | 208.65 | ||
| Mean | 26.66 | 0.283 | 248.37 |
Bedding planes (dotted line in Fig. 7a) were set in shale layers of the model, and a lithologic interface was set at sandstone-shale contact (Table 4), considering the existence of abrupt lithologic interface between sandstone and shale. To quantitatively characterize interface strength, dimensionless interface strength was defined according to the relationship between cohesive unit strength values of reservoir and interface layer, namely:
Table 4 Key parameters of cohesive units in numerical simulation of cross-layer fracturing in shale oil reservoir.
| Element type | Parameter | Value/MPa |
|---|---|---|
| Cohesive elements not at interface or beddings | Normal stress | 6.0 |
| First tangential stress | 20.0 | |
| Second tangential stress | 20.0 | |
| Cohesive elements at sandstone-shale interface | Normal stress | 1.2 |
| First tangential stress | 4.0 | |
| Second tangential stress | 4.0 | |
| Cohesive elements of shale bedding | Normal stress | 2.0 |
| First tangential stress | 10.0 | |
| Second tangential stress | 10.0 |
Three variables, namely fracturing location, fracturing fluid displacement, and dimensionless interface strength, were set for numerical simulation.
2.3. Numerical simulation results
In the shale oil reservoir simulated in this paper, shale and sandstone layers alternate in the longitudinal direction. HFs had different shapes when propagating in different lithologic strata during fracturing. Fig. 8 shows a cloud atlas of displacement after fracturing when the perforation is located in the sandstone layer, at a displacement of 1.8 m3/min and dimensionless interface strength of 0.4. Comparing Fig. 8 with Fig. 3 shows that the fracture morphology obtained by numerical simulation is consistent with the typical fracture morphology from true triaxial fracturing experiments on cores. It can be seen that HFs had different shapes when extending to different horizons. When HFs extended to the shale stratum with developed beddings, they were ladder-shaped; when HFs extended to tight sandstone stratum, they were cross-shaped; when HFs met NFs in fractured sandstone stratum, they were in straight line (Fig. 8).
Fig. 8.
Fig. 8.
Displacement cloud atlas atdifferent times during fracturing in sandstone stratum.
The MMIXDME data (M) of the fracture type of damaged cohesive units was extracted. The M value of 1 means that the unit had shear damage, and the M value of 0 means that the unit had tensile damage, and the value between them means tensile-shear mixed damage (Eq. (5)). The location map of damaged units in formation was plotted in Matlab (Table 5).
Table 5 Locations of damage units in simulations of cross-layer fracturing of shale oil reservoirs.
| Fracturing position | Q=0.6 m3/min γ=0.2 | Q=0.6 m3/min γ=0.4 | Q=1.8 m3/min γ=0.2 | Q=1.8 m3/min γ=0.4 |
|---|---|---|---|---|
| Fracturing from a sandstone layer |  |  |  |  |
| Fracturing from a shale layer |  |  |  |  |
| Fracturing from the sandstone and shale layers simultaneously |  |  |  |  |

where ${{G}_{\text{T}}}\text{=}{{G}_{\text{n}}}\text{+}{{G}_{\text{s}}}\text{+}{{G}_{\text{t}}}$
It was found from Table 5 that when HFs expanded inside the sandstone and shale, the M value was closer to 0, and the fracture type was mostly the tensile type. Whether fracturing in sandstone layer or in shale layer, the HFs diverted along with the sandstone-shale interface. Clearly, the sandstone-shale interface inhibited the fracture height extension. However, for the simultaneous fracturing in two layers, the HFs hardly diverted along with the sandstone-shale interface, and the inhibition of the sandstone-shale interface on fracture height growth was not obvious. In general, HFs tend to propagate vertically in sandstone but laterally in shale due to the induction of bedding.
2.3.1. Influence of fracturing location on hydraulic fracture propagation
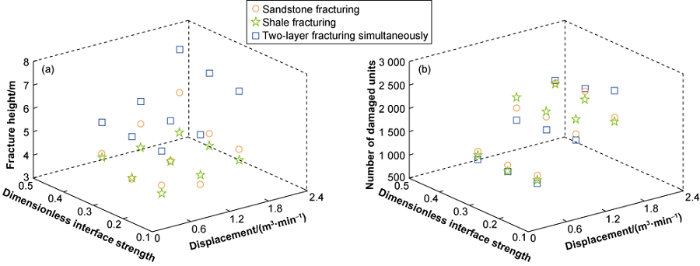
To show the influence of multiple factors more intuitively, the fracture height and number of damage units of each model after fracturing were counted, and the three-dimensional scatter diagram considering multiple factors was drawn in Matlab (Fig. 9).
Fig. 9.
Fig. 9.
Simulation results of fracture heights and number of damage units of different fracturing models of shale oil reservoir.
At a given dimensionless interface strength and fracturing fluid displacement, fracture heights of different fracturing location models from large to small are roughly two-layer simultaneous fracturing, fracturing in sandstone layer, and fracturing in shale layer. The two-layer simultaneous fracturing model was perforated in layers ④ and ⑤, the HFs started to develop from two perforation points, and the fracture height extended the farthest. In the sandstone fracturing model (Model sandstone), fracturing fluid was injected from the sandstone layer, and the HFs started and extended longitudinally from the sandstone with unobvious laminae, and the fracture height was greater than the shale fracturing model. In the shale fracturing model, the shale layer was perforated, the HFs penetrated several beddings vertically in the shale and then were blocked, so the HFs were the smallest in height.
The influence of fracturing position on the number of damaged units varies at different displacements. At low displacement, the numbers of damaged units from high to low are corresponding to sandstone fracturing, shale fracturing, and simultaneous fracturing of sandstone and shale layers. At medium displacement, the numbers of damaged units from high to low are corresponding to shale fracturing, sandstone fracturing, and simultaneous fracturing of two layers. At high displacement, the numbers of damaged units from high to low are corresponding to two-layer simultaneous fracturing, sandstone fracturing, and shale fracturing. In combination with Table 5, it is found that at low displacement, the lateral expansion of fractures in the sandstone fracturing and shale fracturing models increased the total number of damaged units; at high displacement, the expansion of HFs in the fracture height direction in the two-layer simultaneous fracturing model increased the damaged units. The simulations show that using the same fracturing parameters, the simultaneous fracturing of two layers effectively increased the height of HFs. Mutalik et al.[36] analyzed the production data of two-layer simultaneous fracturing in horizontal wells and single-layer fractured wells in the Fort Worth Basin and found that more complex fracture network was formed near the two-layer simultaneous fracturing wells, and the output was greatly improved, which was consistent with the simulation results in this work.
2.3.2. Influence of fracturing fluid displacement on HF propagation
When the dimensionless interface strength and fracturing layer were constant, the fracture height and number of damaged units of the shale oil reservoir increase with the increase of displacement. In combination with Table 5, it is found that with the increase of fracturing fluid displacement, the HFs in the reservoir will penetrate more layers longitudinally and extend farther along the interface. This is because the volume of injected liquid increases per unit time, the energy at the hydraulic fracture tip increases, so the cohesive units are more easily damaged. For the thin and low-permeability layers in shale oil reservoirs, the higher the displacement, the more complicated the connection between HFs and NFs, and the more conducive to fracture extension.
2.3.3. Influence of dimensionless interface strength on fracture propagation
When the fracturing location and fracturing fluid displacement were constant, the fracture height and number of damaged units of the shale oil reservoir models increase with the increase of the interface strength. It is found from Table 5 that when the strength of the sandstone-shale interface increases, the diversion of HFs along the shale bedding decreases, so the HFs vertically extend further and have a better penetration effect, resulting in more damaged units on the whole. This is because as the strength of the interface cohesive units increases, the cohesive elements reaching the initial damage condition decrease, and the fracture is more difficult to divert. At the displacement of 1.8 m3/min, the damaged units of the two-layer simultaneous fracturing model decrease with the increase of interface strength. Under the combined conditions of high displacement and two-layer simultaneous fracturing, with the decrease of the interface strength, the contribution of the fracture diversion along the interface to the number of damaged units compensates the decrease of damaged units due to smaller fracture height, resulting in more damaged units with the decrease of interface strength. Hou et al.[13] found that NFs with weak cementing strength increased the diversion behavior of HFs through a large number of true triaxial physical simulation experiments, and the simulation results in this work are consistent with their physical simulation results.
2.3.4. The number of production layers connected by hydraulic fractures
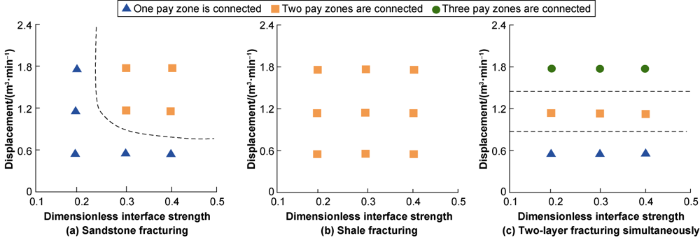
The number of production layers connected was counted under different fracturing locations, fluid displacements, and dimensionless interface strengths, and a control chart was drawn (Fig. 10). During fracturing in sandstone, when the dimensionless interface strength was lower than 0.3 or the displacement was lower than 1.2 m3/min, the HFs could only penetrate one production layer; during fracturing from the shale layer, the fractures connected two production layers; in the two-layer simultaneous fracturing, at the displacements of 0.6, 1.2, and 1.8 m3/min, 1, 2, and 3 production layers were communicated, respectively.
Fig. 10.
Fig. 10.
The influence of interfacial strength and displacement on the number of connected production layers.
Stratum conditions have a great impact on the communication of production layers. The fracture height in the fracturing from the sandstone layer is larger than that of the shale layer. However, it can be seen from Table 5 that when the shale layer was perforated, two pay zones, layer ① and layer ⑤ were connected. In an actual fracturing operation, it is essential to select the appropriate perforation position for connecting the most production layers when perforating in a single position. When perforating in the shale layer in the middle of the upper and lower pay zones, although the fractures are limited in height, it is possible to connect more pay zones.
3. Conclusions
During the fracturing of shale oil reservoirs, the HFs expand in different patterns in different lithologic strata. HFs are straight-line shape in naturally fractured sandstone, cross-shaped in tight sandstone, ladder-shaped in shale rock with beddings. Fracture propagation morphology is closely related to lithology, layer thickness, natural fracture development degree, interface property, and controllable fracturing parameters, etc. Different types of rock layers have different damage characteristics. The HFs in tight sandstone extend vertically in strips, and the HFs in shale are likely to expand laterally induced by bedding.
For shale oil reservoirs in the lower sub-member of Sha-3 Formation in the Dongpu sag, Bohai Bay Basin, the height of HFs are larger when fracturing in the sandstone layer than fracturing in the shale layer, while the height of HFs are even larger when fracturing in the sandstone and shale layers simultaneously than fracturing in the single sandstone layer. Therefore, it is important to analyze the development characteristics of the reservoir during fracturing design. It is preferable to fracturing in two or more layers simultaneously to expand the height of HFs effectively.
According to the geological characteristics of the reservoir, the upper and lower layers adjacent to the pay zone with good cementation can be selected to fracture simultaneously, and fracturing parameters can be adjusted to effectively control the fracture shape, make the fractures connect more production layers, and obtain larger stimulated volume.
Nomenclature
D—damage variable;
E—elastic modulus, Pa;
Gn—Type I tensile fracture energy, J;
Gs—Type II tensile fracture energy, J;
Gt—Type III tearing fracture energy, J;
GT—total fracture energy of fracture unit, J;
i—indicators of first and second tangential stresses, i=1, 2;
M—the value of MMIXDME;
Q—displacement of fracturing fluid, m3/min;
Ss, St—shear strength in the first tangential direction and the second tangential direction, Pa;
T—the tensile strength, Pa;
TI—the tensile strength of the interface layer, MPa;
TR—tensile strength of the reservoir, MPa;
γ—dimensionless interface strength, dimensionless;
δf—effective displacement at failure, m;
δmax—maximum effective displacement during loading, m;
δ0—effective displacement at the initial evolution of damage, m;
ε—strain;
σh—minimum horizontal principal stress, MPa;
σH—maximum horizontal principal stress, MPa;
σn—normal stress, Pa;
σs, σt—shear stress in the first tangential direction and the second tangential direction, Pa;
σv—vertical ground stress, Pa;
τI,i—cohesion in the first or second tangential direction at the interface layer, MPa;
τR,i—cohesion in the first or second tangential direction of the reservoir, MPa.
Subscripts:
n—normal direction;
s, t—two tangent directions.
Reference
Geological characteristics of shale rock system and shale oil exploration breakthrough in a lacustrine basin: A case study from the Paleogene 1st sub-member of Kong 2 Member in Cangdong sag, Bohai Bay Basin, China
Optimization of refracturing timing for horizontal wells in tight oil reservoirs: A case study of Cretaceous Qingshankou Formation, Songliao Basin, NE China
Investigation of hydraulic fracture networks in shale gas reservoirs with random fractures
DOI:10.1007/s13369-015-1829-0 URL [Cited within: 1]
An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials
Influence of geologic discontinuities on hydraulic fracture propagation (includes associated papers 17011 and 17074)
Fracturing mechanism of shale gas reservoir with variable pump rates
Criteria for judging whether hydraulic fractures cross natural fractures in shale reservoirs
Experimental investigation on influence of discontinuities on hydraulic fracture propagation in three-dimensional space
Experimental research on the morphology of hydraulic fractures in deep shale under high difference of in-situ horizontal stresses
Study on fracture propagation behavior in ultra-heavy oil reservoirs based on true triaxial experiments
The effect of argillaceous interlayers on integrative fracturing of sandstone-mudstone interbedding reservoir with huge thickness
An evaluation method of volume fracturing effects for vertical wells in low permeability reservoirs
Experiments on the non planar extension of hydraulic fractures in fractured shale gas reservoirs
Experimental investigation on propagation geometry of hydraulic fracture in compact limestone reservoirs
A novel approach of stimulation based on fracture controlling optimization and design
Experimental investigation on fracture geometry in multi-stage fracturing under tri-axial stresses: 8th Asian Rock Mechanics Symposium
Fracture initiation and propagation in a deep shale gas reservoir subject to an alternating-fluid-injection hydraulic-fracturing treatment
Optimization workflow for stimulation-well spacing design in a multiwell pad
Effects of laminated structure on hydraulic fracture propagation in shale
Study on the mechanism of shale bedding on the vertical propagation of fracturing fractures
Effect of hydraulic fracture and natural fractures interaction in fracture propagation: 13th ISRM International Congress of Rock Mechanics
Interaction between hydraulic fractures and natural fractures: Current status and prospective directions
DOI:10.1007/s13202-019-00778-3 URL [Cited within: 1]
Natural and hydraulic fracture density prediction and identification of controllers
Experimental investigation on fracture geometry in multi-stage fracturing under tri-axial stresses: ISRM International Symposium-8th Asian Rock Mechanics Symposium
Effect of shear slippage of vertically crossed layer interface on hydraulic fracture height growth: 53rd US Rock Mechanics/Geomechanics Symposium
Experimental and numerical study of hydraulic fracture geometry in shale formations with complex geologic conditions
Hydraulic fracture-height containment by permeable weak bedding interfaces
A 3-D hydraulic fracture propagation model applied for shale gas reservoirs with multiple bedding planes
DOI:10.1016/j.engfracmech.2020.106872 URL [Cited within: 1]
The influence of fracture network connectivity on hydraulic fracture effectiveness and microseismicity generation: 47th U.S
Integrating fully coupled geomechanical modeling with microsesmicity for the analysis of refracturing treatment
Genetic connection between mud shale lithofacies and shale oil enrichment in Jiyang Depression, Bohai Bay Basin
Enrichment rules and exploration practices of Paleogene shale oil in Jiyang Depression, Bohai Bay Basin, China
Reservoir potential evaluation of Es3L shale oil in Dongpu Depression
Formation conditions and “sweet spot” evaluation of tight oil and shale oil
Fracture path interaction of two adjacent perforations subjected to different injection rate increments
Case history of sequential and simultaneous fracturing of the Barnett shale in Parker County