Introduction
A common method of oil production from terrigenous reservoirs is reservoir flooding, in which oil from a porous medium is displaced by water or solutions with surfactants or polymer additives. Several works have appeared recently in which nanofluids are proposed to be used as a promising agent for waterflooding and enhanced oil recovery[1,2,3]. A nanofluid is considered to be suspension (usually based on water) with the addition of nanoparticles of various compositions. Their size and concentration, the physical properties of the nanosuspension can vary significantly depending on the substance of the particles. Nanofluids are now used in a large number of different applications[1,2,3,4,5]. Concerning the oil displacement process, the most important physical properties are viscosity, wettability angle and interfacial tension coefficient. These properties of nanosuspensions substantially depend on the type, concentration and size of nanoparticles. This makes it possible to control the properties of the flooding fluid. In this regard, a large number of studies have recently been carried out to study the possibility of using various nanosuspensions to increase oil recovery during waterflooding. Both laboratory experiments[6-8] and various numerical models[9-25] are used for studying the process of waterflooding with the use of nanoparticles.
Models used for numerical simulation of nanosuspension flows during oil displacement from a porous medium can be divided into two groups: one is that rocks are regarded as homogeneous porous media[9-16] and solved based on Darcy's equation; the other is the direct numerical model (pore scale model) based on Navier Stokes equation to describe fluid flow in pore space[17,18,19,20,21,22,23,24,25]. One of the first approaches to modeling nanosuspension flows was developed by Ju et al.[9,10]. A one-dimensional model of flow in a porous medium based on Darcy's law was considered in their work, but did not consider the wettability changes caused by nanoparticles. El-Amin et al.[11,12] extended Ju et al. approach for a two-dimensional case for an anisotropic porous medium taking into account capillary forces and Brownian motion. The wetting effects were also disregarded as well. Feng et al.[13] based on the model developed by El-Amin et al. conducted numerical studies on the influence of such parameters as duration and volume of injection of nanosuspension on the efficiency of oil recovery, but capillary pressure and changes in wettability were not considered. The study of changes in the rock wettability and formation calmatation by nanoparticles using the Darcy model was carried out by Sepehri et al.[14]. Yu et al.[15] simulated the flow of nanofluids in dolomite cores, and found that the salinity of water has a significant effect on the migration of nanoparticles. Rahmani et al.[16] presented a model of the motion of superparamagnetic nanoparticles within the formation for sounding the rock during tracer diagnostics.
Much less work is devoted to the study of oil displacement by nanofluid using pore-scale modeling. In this case, the structure of the porous medium is described by the computational grid. This approach requires significant computing resources. 2D models are mainly used in this direction. However, in this case, there is no need to use such empirical constants as porosity and phase permeability of the medium. Both the mixture model[17-20] and the immiscible fluid model with the calculation of the phase interface[21,22,23,24,25] can be used to describe the multiphase flow of this approach. The equations of conservation of mass, momentum and energy are solved for the entire calculated volume in the mixture model. The physical properties of the liquid in each control volume are determined according to the mixture rule based on the known nanoparticles’ concentration. Gharibshahi et al.[17] studied the influence of pore shape and distribution in two-dimensional microscopic model on oil displacement process through miscible model, and discussed the influence of type, concentration and size of nanoparticles and temperature of injected fluid on oil displacement effect based on this[18], but still did not consider the influence of wettability.
In contrast to the mixture model, the models based on the VOF method directly calculate the interface between the phases of immiscible liquids, hereby allowing for an accurate consideration of the surface tension forces between the two liquids and the contact angle. It is noted in most experimental works that these properties play a key role in increasing oil recovery when injecting nanosuspensions into the reservoir[6,7,8]. It should be noted that the VOF method is very widely used in research related to enhanced oil recovery (injection of surfactants, polymers, CO2, steam). However, there are very few works related to modeling VOF by the method of oil displacement by nanofluid. In this case, either two-dimensional models[21] or simplified models of individual pore channels are used. For example, in the work of Zhao and Wen[22], the displacement of oil by nanofluid from two round pores connected by a narrow channel (throat) was investigated.
In this study, a three-dimensional microscopic core model is used to simulate the oil displacement process of nanofluids. The model is very close to the real core in structure. VOF is used to study the effects of mass fraction and particle size of nanoparticles, flow rate of displacement fluid, oil viscosity and core permeability on oil displacement efficiency of nanofluids.
1. Experiments
Systematic experimental studies of IFT and wettability in nanosuspension-oil-rock systems were carried out to obtain these data for accurate numerical simulation. A detailed description of the results of experiments on the effect of nanoparticles on wettability can be found in our recent work[26]. Light oil (density 0.831 g/cm3, viscosity 7.8 mPa·s) was used in the experiments.
Table 1 Measured particle sizes in the powder (PS), specific surface area (SSA), average particle size (APS) in the suspension, and zeta-potential (ζ) of the NPs used.
| Materials | PS/ nm | Manufacturer | SSA/ (m2•g-1) | APS/ nm | ζ/mV |
|---|---|---|---|---|---|
| SiO2 | 5 | Aerosil | 380 | 12 | -13.9 |
| SiO2 | 18 | Bardakhanov | 149 | 40 | -19.8 |
| SiO2 | 22 | Sigma Aldrich | 110 | 30 | -38.0 |
| SiO2 | 50 | Bardakhanov | 55 | 130 | -37.4 |
The nanopowder of SiO2 was added to the distilled water to prepare nanofluid, after which the resulting suspension was thoroughly mechanically mixed. The average size of nanoparticles (NP) in the powder varied from 5 to 50 nm. The nanoparticle concentration ranged to 1%. The suspension was processed in an ultrasonic dispersant to break down the nanoparticle conglomerates. The stability of the obtained suspension was investigated using the TurbiscanLAB analyzer. It was shown that the studied nanosuspension was stable for ten days from the moment of preparation. The average particle size and zeta-potential in suspensions were measured using an acoustic and electroacoustic analyzer DT1202. This device allows measuring the size of NPs directly in a liquid. Because NPs are subject to aggregation, the particle size in the liquid may differ from the NP size in the original powder. Data on the average size and size distribution of particles in the liquid are shown in Table 1. As is seen, in some cases, the particle sizes in the liquid differ from those in the original powder. However, the size of the particles in the liquid is proportional to the size of the original NPs. For most of the suspensions considered, the absolute value of the zeta-potential exceeds 20, which ensures their high colloidal stability.
Measurement of interfacial tension and the wetting angle was carried out by means of IFT-820-P automatic tensiometer. The operation principle of IFT-820-P tensiometer is based on the hanging drop method, in which the surface tension is determined through measurements of the geometric parameters of the drop of the investigated liquid. The measurement results were processed using the DropImage Advanced software. The final data were obtained by averaging over four independent measurements. Data variances in the experiments did not exceed 5%. The measuring method of the surface tension coefficient was tested on water and ethylene glycol. At that, good agreement with the reference data was obtained[27,28].
The measurement of the nanosuspension viscosity coefficient was carried out using OFITE HPHT viscometer. The viscosity measurement error was about 2%. The density of the nanosuspensions was measured by measuring the mass with a precision balance (Mettler Toledo) and the volume using graduated beakers. The density measurement error was about 1%.
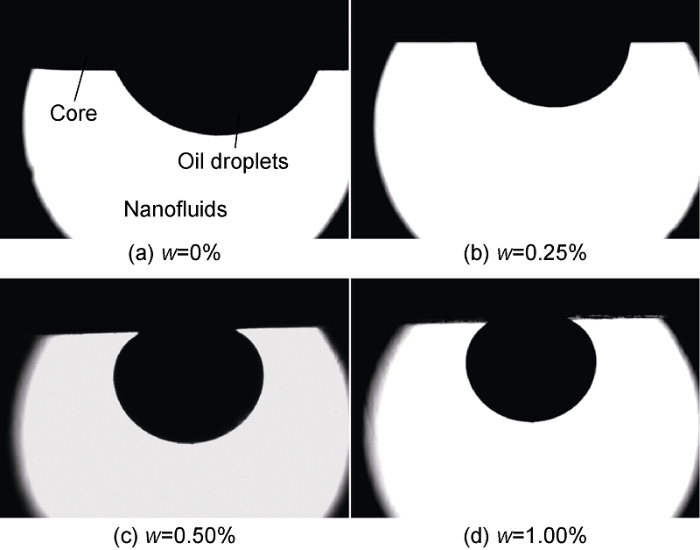
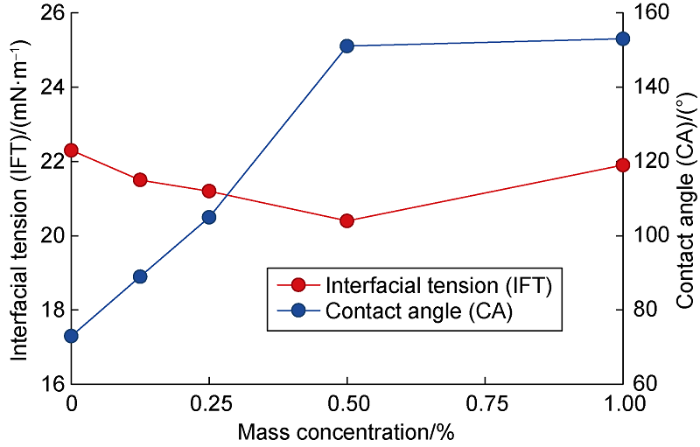
Figs. 1 and 2 show the measurement results for a nanofluid with SiO2 particles with an average size of about 5 nm. It has been shown that the nanoparticles concentration significantly affect the oil wetting characteristics of the rock (Fig. 1). Influence analysis of the nanoparticle additives on the wetting angle has shown that oil contact angle (internal) increases with increasing concentration of nanoparticles and also very significantly, namely, from 73° to 153°. Thus, it was found that the addition of nanoparticles to the liquid significantly worsens the wettability of the rock by oil. In fact, the addition of 1% of nanoparticles to water makes core non-wettable by the oil. It was shown that with an increase of nanoparticle mass fraction IFT changes weakly within a wide range of nanoparticle concentrations (Fig. 2). The maximum reduction of interfacial tension with the addition of 5 nm nanoparticles was about 7%.
Fig. 1.
Fig. 1.
Photos of oil droplets in nanofluids on the surface of core at different nanoparticle concentrations.
Fig. 2.
Fig. 2.
Interfacial tension (IFT) and contact angle (CA) of nanosuspension-oil versus SiO2 nanoparticle mass concentration.
The effect of the NP size on the oil wettability characteristics of a rock in a nanosuspension has been experimentally studied. The addition of SiO2 NPs with average sizes from 5 to 50 nm to water is considered. The NP mass concentration in the measurements was equal to 0.5%. The influence of nanoparticle size on the contact angle and interfacial tension of nanofluid-oil-rock at 25℃ was studied (Table 2). As the NP size decreases, the wetting angle at the oil/nanosuspension/rock boundary increases. Thus, with a decrease in the NP size, the oil-washing ability of the nanosuspension increases. As can be seen, the interfacial tension decreases with increasing nanoparticle size. The IFT between oil and nanofluids decreases about 25% with the increase of nanoparticle size.
Table 2 Measurement results of suspensions containing various sizes of SiO2 Nanoparticles.
| Particle size/ nm | CA/ (°) | IFT/ (mN·m-1) | Viscosity/ (mPa·s) |
|---|---|---|---|
| 5 | 151 | 20.4 | 0.9113 |
| 18 | 117 | 19.3 | 0.9050 |
| 22 | 109 | 17.1 | 0.9034 |
| 50 | 91 | 15.6 | 0.8971 |
At 25 °C, when the mass fraction of 5 nm SiO2 nanoparticles is 0.125%, 0.25%, 0.5%, 1%, the corresponding viscosity of nanofluids is 0.896 4, 0.897 6, 0.911 3, 0.983 6 mPa·s, and the density is 0.997 7, 0.998 4, 0.999 7, 1.002 5 g/cm3, respectively. As can be seen, with the addition of 1% of nanoparticles, the viscosity increases by about 9%. This is significantly higher than the value predicted by the classical viscosity theory for coarse suspensions. For example, Einstein's theory $\mu ={{\mu }_{0}}\left( 1+\frac{5}{2}\varphi \right)$ gives a viscosity increase of about 1% for a particle concentration of 1%. It is known that Einstein's formula describes well the viscosity of coarsely dispersed microsuspensions at low particle concentrations. However, the nanosuspensions’ viscosity behavior is not described by classical theories[23] and this formula gives large errors for nanosuspensions. As the NP size decreases, the viscosity of the nanosuspension increases (Table 2). This is also an important difference between nanosuspensions and classical suspensions for which the viscosity does not depend on the particle size[29]. The obtained experimental data on the interfacial tension coefficient, the contact angle and viscosity of nanosuspension were further used in systematic numerical investigation.
2. Mathematical model and numerical technique
A systematic numerical study of the oil displacement from the 3D porous rock micromodel using nanosuspension was done. Only laminar flows are considered. The VOF method[30] was used to simulate a two-phase flow in a porous medium. This model can simulate immiscible liquid-liquid multicomponent flow by solving conservation of momentum and using the volume fraction of each phases. In the consideration introduces the volume fraction of the displacing fluid α and volume fraction of the oil β. Since α + β =1 it is sufficient to use only the volume fraction of the displacement fluid α. In the first case, water, which poorly wets the rock, displaces the oil, which wets the rock well. In this case, the density and viscosity of the mixture included in the Navier-Stokes equations are determined as follows:
The mass conservation equation in this case has a standard form:
Here v is mixture velocity vector, a single momentum equation is solved to define it:
The following transfer equation is solved to simulate the movement of the interface in the process of oil displacement:
The continuum surface force (CSF) algorithm was used by Brackbill et al.[31] to simulate surface tension. For this method, surface tension effects are modeled by adding a source term in the momentum equation:
where
$k=\nabla \left( \frac{n}{\left| n \right|} \right)$ $n=\nabla \alpha $
On the walls of the computational domain, the normal vector is determined using the following expression:
In the calculations used experimentally measured values of the viscosity, density, interfacial tension and contact angle of nanosuspension depending on particle concentration φ and size. The numeric technique used in this paper and the results of its testing are described in detail in the references [32-33]. To solve the system of nonlinear differential equations (3-5), we used the FVM (Finite-Volume) method. The coupled between the velocity field and pressure is realized using the SIMPLEC (Semi-Implicit Method for Pressure Linked Equations-Consistent) algorithm. The PRESTO (PREssure STaggering Option) scheme for calculation continuity balance was used. A second-order implicit scheme was used to approximate the unsteady terms of the transport equations. A second-order central-difference scheme was used to approximate the convective terms of the Navier-Stokes equations. A TVD scheme with HRIC limiter was used to solve the transport equation (5).
3. Results of numerical research
3.1. Statement model
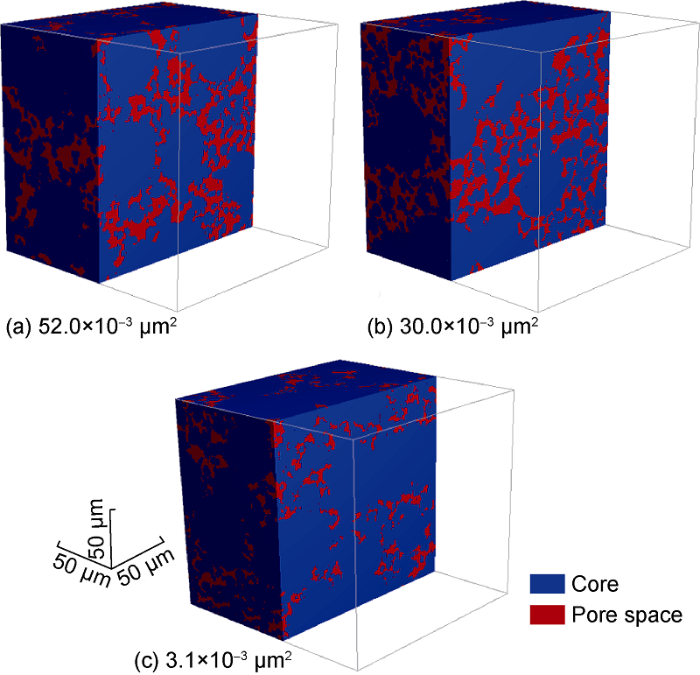
Simulation of oil displacement from the reservoir model by using nanofluid processes has been carried out. This work presents modeling in a three-dimensional setting on digital core models, close to real core samples in their structure. The porosity of the cores was 25, 20 and 7%. Permeability values for digital cores of various types varied in the range from 3.1 to 52×10-3 μm2. The minimum flow pore size was significantly larger than the minimum average nanoparticle size. Therefore, in this study, the effect of nanoparticles on core permeability was neglected. The computational domain was a cube with an edge size of 150 μm. Fig. 3 show core models of different permeability. Here the rock is painted in blue, the pore space in red.
A computational grid consisting of 3 500 000 cells was used for the calculations. A series of methodological
Fig. 3.
Fig. 3.
Digital core model with different permeability.
calculations were carried out in order to determine the influence of the computational mesh detailing on the modeling accuracy. We operated on the experimentally measured data on viscosity, interfacial tension, and contact angle for calculations. Nanosuspensions with silicon oxide particles with an average particle size of 5 nm were used. The mass concentration of particles in the calculations varied from 0 to 1%. The viscosity of the base oil model was set equal to 7.8 mPa∙s; the density was 0.831 g/cm3. The water/oil interfacial tension was measured to be 22.5 mN/m. The following boundary conditions were set for modeling. The displacing fluid’s velocity was set on the upper edge of the computational domain varied from 7.8×10-6 to 2.3×10-1 m/s. The conditions of free exit were set on the lower face of the computational domain. The adhesion conditions were set on the side walls of the computational domain.
The calculation was carried out in a non-stationary setting. At the beginning of the calculation, the pore space was saturated with oil. The initial water saturation was zero. The dynamics of the displacement front advance, the oil breakthrough time, the residual oil saturation, the instantaneous and final value of the ORF and the value of pressure losses at the inlet and outlet from the computational domain were investigated as a result of the simulation.
3.2. The effects of nanoparticle mass fraction
For the study included an investigation of the effect of the particle concentration in nanosuspension on the efficiency of oil displacement, a basic calculation option was considered: core permeability was 3.1×10-3 μm2, oil viscosity was 7.8 mPa∙s, displacement fluid velocity was 7.05×10-4 m/s. Fig. 4 illustrate the process of oil displacement over time for water and nanosuspension with a mass concentration of particles of 1%. The displacement process is shown using isosurfaces of the volume fraction of the displacing fluid on the walls of the porous medium. It can be seen that the hydrophobicity of rock surface changes to hydrophilicity with the increase of particle mass fraction in nanofluid flooding. Analysis of the local displacement front inside the pore channels showed that the water phase moves along the porous medium walls for a water-wet system (w = 1%). As for an oil-wet system (w = 0), the water phase moves along the pore channels’ center, leaving the walls wet with oil. Therefore, the waterflooding front is much more uniform and filling in the cross-section of the pore channels for the nanosuspension in comparison with the displacement by water. The displacement front for nanosuspension is much closer to piston displacement. The proportion of the volume of pore channels occupied by the flow of nanosuspensions also significantly increases. The nanosuspension moves with a more uniform front over the entire core section. Whereas water moves predominantly in one designated direction, leaving large volumes of oil not swept away by movement. This can be clearly seen in Fig. 4. The characteristic water breakthrough time is about 0.013 sec. for this option, while nanosuspension breakthrough time is 0.027 sec.
Fig. 4.
Fig. 4.
Distribution of water and nanosuspension in a porous medium at varied time. Flow direction of displacing fluid from top to bottom.
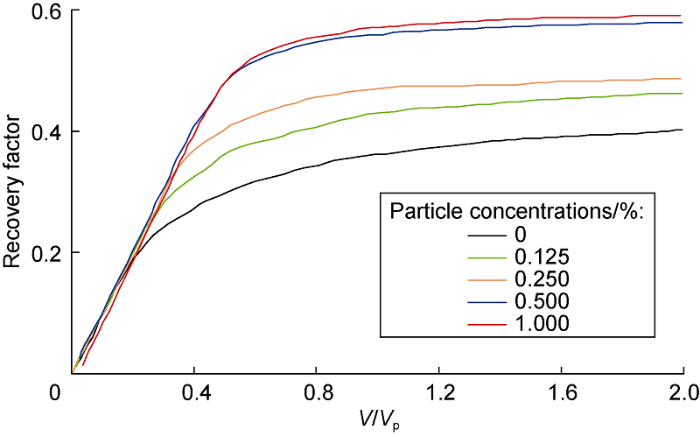
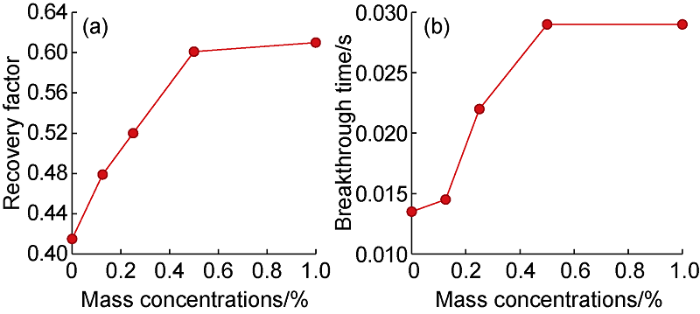
The oil recovery factor for nanosuspensions with different particle concentrations is shown in Fig. 5, where V/Vp is the ratio of the volume of injected fluid to the pore volume. As can be seen, the oil recovery factor increases with an increase in particles’ concentration in the displacing fluid. It is also clearly seen from this graph that the time for stopping oil from leaving the core increases with an increase in particles concentration. This also indicates almost complete washout. The dependence of the final ORF value on the mass concentration of particles is shown in Fig. 6a. The ORF increases with an increase in the mass concentration of particles. Thus, as a result of modeling, it was shown that 0.25% of siliconoxide nanoparticles allows an increase in the recovery factor by about 10% compared to water. An increase in nanoparticles’ concentration to 0.5% allows an increase in oil recovery factor by about 19% compared to water. When the mass fraction changes from 0.5% to 1.0%, the change of contact angle and interfacial tension is not obvious, so increasing the mass fraction of particles will not further increase the oil recovery. As already mentioned, a more uniform oil displacement profile by nanosuspension leads to a noticeable increase in the breakthrough time water. These data are shown in Fig. 6b. This is what determines the additional volume of oil washed out from the porous medium by the nanosuspension.
Fig. 5.
Fig. 5.
ORF for SiO2 nanosuspensions with different particle concentrations.
Fig. 6.
Fig. 6.
Dependence of the final oil recovery factor (a) and the breakthrough time for water (b) on the mass concentration of SiO2 particles.
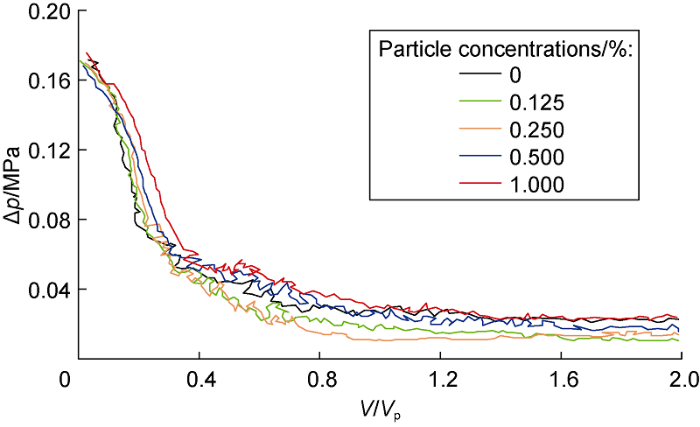
Fig. 7 shows the dependence of the pressure drop between the inlet and outlet from the computational domain on relative volume nanosuspension with different particle concentrations. It is clearly seen that the process of penetration of a displacing fluid into an oil-saturated porous medium is accompanied by pressure pulsations associated with micro-separation of oil from the rock walls. After the displacement fluid completely breaks through to the exit of the computational domain, the pressure drop decreases. Pressure pulsations stop, and the flow becomes quasi-stationary. In this case, although the nanosuspension has a higher viscosity (by about 10%), the value of the pressure drop for the nanosuspension is generally lower than for pure water. This happens because that the addition of nanoparticles reduces capillary pressure by reducing IFT and improving rock’s wettability. But with a further increase in the concentration of nanoparticles, the total pressure increases due to an increase in the interfacial tension and viscosity of displacing fluid.
Fig. 7.
Fig. 7.
Pressure drop during displacement for SiO2 nanosuspensions with different particle concentrations.
3.3. The effects of nanoparticle size
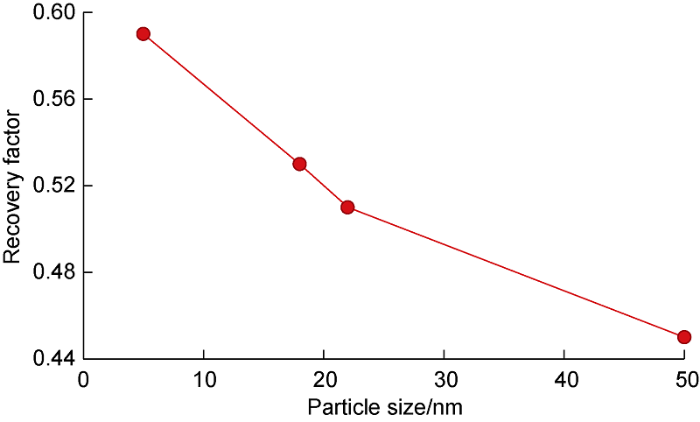
Calculations were performed for silicon oxide suspensions with four different average particle sizes (5, 18, 22, 50 nm). The mass concentration of particles was 0.5%. Experimental data on the contact angle, interfacial tension and viscosity coefficient of nanosuspensions with different particle sizes are given in Table 2. The viscosity and water wettability increase with decreasing nanoparticle size, while the ITF, on the contrary, decreases. In this case, the contact angle changes most significantly with decreasing of the nanoparticle size. Increasing the viscosity and wettability of the drive fluid is beneficial for increasing the ORF. Thus, nanoparticle size is main factor that can control displacement efficiency. It is possible to change the displacement mode from hydrophobic to water-wet by reducing the nanoparticles’ size in the nanosuspension. Numerical simulation results show that this leads to an increase in the volume of displaced oil. The oil recovery factor increases by about 29% as the size of SiO2 nanoparticles decreases from 50 nm to 5 nm. The dependence of the oil recovery factor for nanosuspensions with different particle sizes is shown in Fig. 8. Thus, it is more advantageous to use smaller nanoparticles in order to increase oil recovery. However, it should be noted that a decrease in the NPs size decreases their effect on the IFT value. In this case, the IFT increases by about 30% as the particle size increases. From the point of view of oil recovery, it is more beneficial to reduce the interfacial tension. In this case, it did not have a significant impact. Increasing wettability with decreasing nanoparticle size had a more significant effect on ORF than increasing IFT. However, there should be some optimal nanoparticle size in the general case that would maximize ORF at a given concentration.
Fig. 8.
Fig. 8.
ORF dependence on the particle size.
3.4. The influences of the displacement fluid flow rate
Though the influence of the displacement fluid flow rate on the displacement characteristics is well studied[34,35,36,37], it was shown that the residual oil saturation depends on the value of the capillary number, which plays an important role in the tasks of increasing oil recovery. Here we use the following definition Nco=vμ/σ. Previous studies have shown that the residual oil saturation decreases monotonically, if Nco exceeds the immobilization threshold. It was found in experiments on model cores that the critical value of the capillary number depended on the wettability and ranged from 10-5 to 10-3. A series of calculations was carried out to study this, in which the speed of the displacing fluid varied in the range from 7.8×10-6 to 2.3×10-1 m/s. This corresponds to the capillary number range from 3.6×10-7 to 1.1×10-2. The remaining oil distribution in the core section after water flooding at different displacement rates and nanofluid flooding with 1% particle mass fraction injected 3 times of pore volume is shown in Fig. 9. In the process of nanofluid displacement, because the pore wall is wet, the nanofluid displacement along the pore channel is more uniform and more oil is washed out. At this time, the remaining oil is distributed in the center of the pore channel. During water displacement, the remaining oil is mainly distributed in the retention cavity on the wall of large channel. The action of capillary forces weakens with an increase in the flow rate, and most of the pore channels become available for flow. Therefore, the efficiency of oil recovery is increased.
Fig. 9.
Fig. 9.
The final distribution of the remaining oil for different values of the capillary numbe. Flow direction of displacing fluid is from top to bottom.
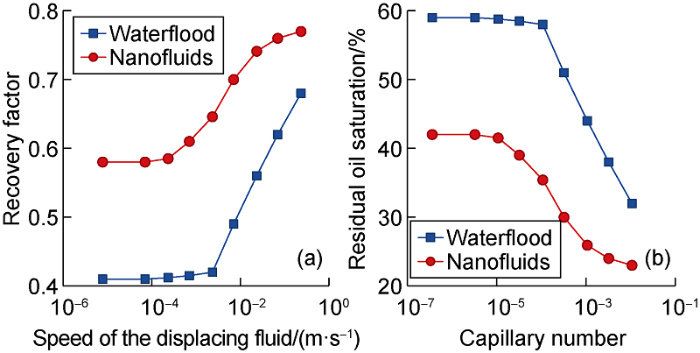
In this study, under the condition of low capillary number, the capillary pressure retained most of the oil in the porous media, so the remaining oil saturation and recovery factor in this model have nothing to do with the displacement rate. When the capillary number reaches the critical value, the remaining oil saturation decreases with the increase of displacement rate, the recovery increases with the increase of displacement rate (Fig. 10). In this mode, the viscous force exceeds the capillary pressure. In the range of displacement speed, the recovery of oil displacement by nanofluids is higher than that of water drive (Fig. 10a). Meanwhile, the influence of nanoparticles on recovery rate decreases with the increase of displacement speed. So, for example, ORF increases by about 1.4 for Nco = 3.6×10-7 (capillary mode) and by 1.14 times for Nco =1.08×10-2 (pressure mode). Thus, the effect of nanoparticles addition on the efficiency of oil displacement is stronger in the capillary mode. Besides, it was found that when nanoparticles are added to the displacing fluid, the immobilization threshold decreases by almost an order of magnitude from about 1×10-4 to 1×10-5 (Fig. 10b). It shows that injection of a small amount of displacement fluid can enhance oil recovery.
Fig. 10.
Fig. 10.
Dependence of the oil recovery factor on the speed of the displacing fluid (a) and the dependence of the residual oil saturation (b) on the capillary number.
3.5. The effects of oil viscosity
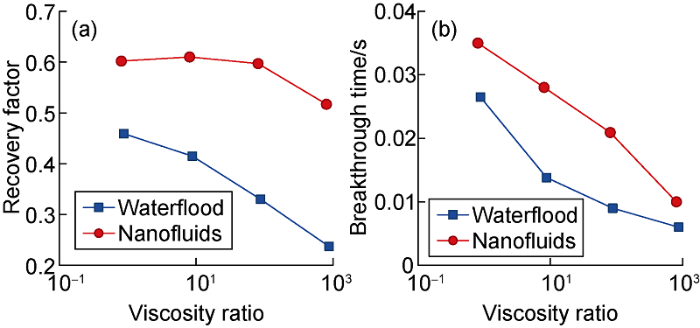
A computational study of oil recovery from a core using nanosuspensions was carried out for oils with different viscosities for the first time. The oil viscosity varied over a wide range of values from 0.00078 to 0.78 mPa s in the calculations. Thus, the ratio of the oil viscosity to the viscosity of the displacing fluid (μr) varied from 0.8 to 800. The mass concentration of silica particles in the suspension was 1%. The calculations were carried out for the displacement fluid flow rate corresponding to the value of the capillary number was 6×10-7 (capillary displacement mode). The core permeability was 3.1×10-3 μm2. Fig. 11 illustrates the process of oil displacement with different viscosities of water and nanosuspensions after injection of three pore volumes. It can be seen that the nanosuspension spreads with a wider displacement front, in contrast to water, which penetrates the core in separate jets. Studies have shown that when high-viscous oil is displaced by water, instability of viscosity is observed. Water displacing high-viscous oil forms local projections at the displacement front, which increase as the oil-water contact moves along the core. This results in “tongues” of flooding, which quickly reach the exit from the core. Also, this leads to a decrease in ORF with increasing viscosity. The movement of the front of the nanosuspension is significantly different. Due to the nanosuspension’s hydrophilic nature, its movement primarily spreads along the walls of the rock. The better wettability of the nanosuspension allows for better washing off the more viscous oil. This makes it possible to achieve an increase in the recovery factor of viscous oil.
Fig. 11.
Fig. 11.
The final distribution of the displacing fluid in the central longitudinal section of the core for different values of the viscosity ratio. Flow direction of displacing fluid is from top to bottom.
Fig. 12a shows that ORF decreases with increasing the viscosity ratio. This is consistent with generally accepted views of references [32-36]. In addition, the graph shows that the 1% addition of nanoparticles to the displacement fluid leads to an increase in the ORF for any viscosity ratio. It was shown that the positive effect of the addition of nanoparticles on ORF increases by increasing the viscosity ratio. So the oil recovery factor for nanosuspension is 1.2 times higher than for water for μr≈0.8, and it is 2.2 times higher for μr≈800. Besides, it is well known that the ORF begins to decline sharply when the viscosity ratio of oil to displacement fluid exceeds 10. Data in Fig. 12a for water confirms this. In this case, as can be seen, such a decrease in ORF begins at μr>100 for nanosuspensions. This means that the injection of nanosuspensions is effective in a broader range of changes in μr. It can be seen from the relationship curve between breakthrough time and viscosity ratio (Fig. 12b) that breakthrough time decreases with the increase of viscosity ratio. Nanofluids have a longer breakthrough time than water and can drive more oil out of the core. Thus, it has been shown that the efficiency of the nanosuspensions use will increase with an increase in the ratio of the viscosities of the oil and the displacing medium.
Fig. 12.
Fig. 12.
Dependence of the recovery factor (a) and breakthrough time on the viscosity ratio μr.
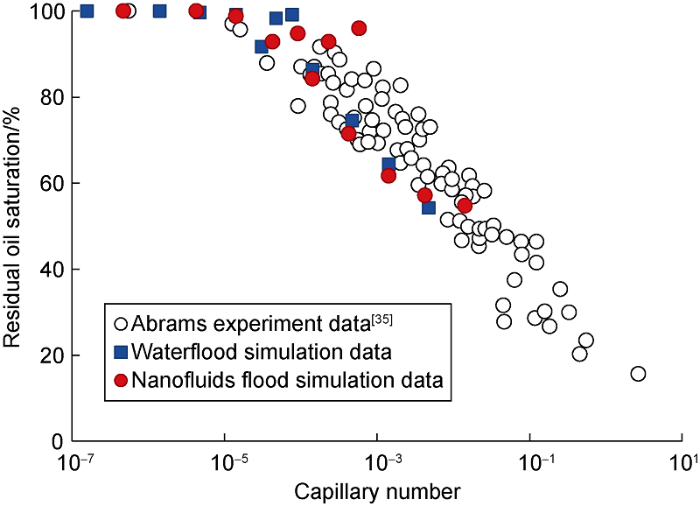
However, there is currently no single universal definition of the capillary number since the residual oil saturation depends on a significant number of factors (displacement rate, fluid viscosity, wettability, porosity, etc.). There are several different approaches for determining the capillary number[34,35,36,37]. The choice of the capillary number essentially determines the critical value of the immobilization threshold for capillary retained oil. Probably the universal approach, generalizing the largest number of various experiments on sandstone, is the determination of the capillary number proposed by A. Abrams[35]:
We used this generalization for our calculated results and compared the normalized residual oil saturation values with the known experimental data. Comparison of the calculated and experimental data is shown in Fig. 13. As can be seen, there is a fairly good agreement between the calculation and experiments, both in the critical value of the generalized capillary number and in the angle of slope of the displacement curve in the pressure section. This demonstrates the reliability of numerical simulations, and, moreover, shows that Abrams' generalization has a fairly universal character.
Fig. 13.
Fig. 13.
Dependence of the normalized residual oil saturation on the generalized capillary number.
3.6. The core permeability influences
Based on the numerical simulation of nanofluid flooding cores with different permeability, considering the low permeability and high permeability reservoir models, the core model permeability is (3.1-52.0)×10-3 μm2. The results show that the number of capillary is 3.6×10-7. The trajectory of nanoparticles in the core model and the three-dimensional distribution of oil after displacement are shown in Fig. 14.
Fig. 14.
Fig. 14.
Trajectories of marker particles colored by the velocity magnitude and final distribution of the oil after flooding with nanosuspension of cores with different permeability. Flow direction is from top to bottom.
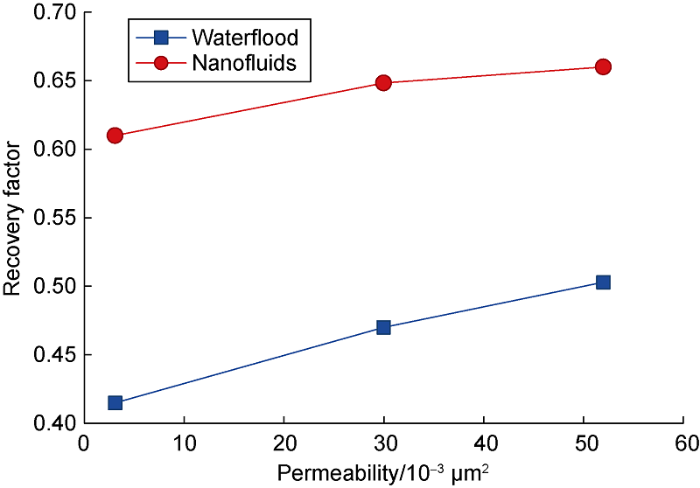
The ORF of reservoir is mainly determined by the property of reservoir, and usually decreases with the decrease of permeability (Fig. 15). This is because the pore channels in the low permeability reservoir model are narrower than those in the high permeability reservoir model. The narrower pore channels and the more remaining oil retained by capillary will make the lower displacement efficiency (Fig. 16).
The effect of nanofluids on oil recovery depends on reservoir permeability, and the performance of adding nanoparticles decreases with the increase of permeability. The results show that compared with water flooding, the oil recovery of nanofluid flooding in low permeability reservoir and high permeability reservoir is increased by 40% and 30%, respectively. The displacing fluid spreads out in a wide front and fills a significant volume of pore space for cores with higher permeability. The nanosuspension effect on the surface wettability characteristics does not play such a significant role on the displacement efficiency there. Oil from wide pore channels is relatively well washed out by water. As for a low-permeable reservoir a large volume of oil is retained by capillary forces in narrow pore channels. The improvement in surface wettability that occurs when nanoparticles are added to the displacing agent begins to play an important role under these conditions. The use of nanosuspensions makes it possible to wash out more of the capillary retained oil (Fig. 16). Thus, it has been shown that nanosuspensions can significantly increase the oil recovery factor for rocks with different permeability values. The effect of using a nanosuspension is enhanced when permeability is decreased.
Fig. 15.
Fig. 15.
Oil recovery factor vs. core permeability.
Fig. 16.
Fig. 16.
The final distribution of the displacing fluid in the central longitudinal section of cores with different permeability. Flow direction of displacing fluid is from top to bottom.
4. Conclusions
The addition of nanoparticles to the displacing fluid significantly affects the process of oil displacement from the porous rock. When the mass fraction of nanoparticles increases to 0.5%, the oil recovery can be increased by about 19% compared with water flooding. The efficiency of oil extraction by nanosuspension depends on the size of nanoparticles. It is found that the ORF value increases with the decrease in nanoparticle size. When nanoparticles are added to the displacing fluid, the oil immobilization threshold decreases by an order of magnitude. The use of nanosuspensions for enhanced oil recovery is most effective in injection modes close to the immobilization threshold. The effect of the addition of nanoparticles on ORF decreases with an increase in the displacement rate. When the viscosity of crude oil is greater and the rock permeability is lower, then the effect of nanofluid flooding on EOR is more obvious.
Nomenclature
Nco—capillary number, dimensionless;
Nco*—capillary number calculated by the method developed by Abrams, dimensionless;
Fs—volume force vector caused by capillary forces, N/m3;
k—curvature of the interface, m-1;
n—normal vector of interface between phases, dimensionless;
nw—normal to the wall vector, dimensionless;
p—static pressure of mixture, Pa;
t—time, s;
v—mixed velocity vector, m/s;
V/Vp—ratio of injected fluid volume to pore volume, dimensionless;
v—fluid velocity in porous media, m/s;
w—mass fraction of nanoparticles, %;
α, β—volume ratio between displacing fluid and oil, dimensionless;
Δp—pressure drop between the inlet and outlet from the computational domain, Pa;
θ(φ)—contact angle at the wall, (°);
μ—viscosity, Pa·s;
μo—oil viscosity, Pa·s;
μr—viscosity ratio between crude oil and displacing fluid, dimensionless;
μw—viscosity of displacingfluid, Pa·s;
μ0—base fluid viscosity, Pa·s;
μ1(φ)—nanofluids viscosity, Pa·s;
ρ—density, kg/m3;
ρ1(φ)—density of nanofluids, kg/m3;
ρ0—density of oil, kg/m3;
σ(φ)—interfacial tension, N/m;
τw—tangential to the wall vector, dimensionless;
φ—volume fraction of nanoparticles, %.
Reference
Recent advancements in PV cooling and efficiency enhancement integrating phase change materials based systems: A comprehensive review
DOI:10.1016/j.solener.2019.11.075 URL [Cited within: 2]
Application of nanotechnology in petroleum exploration and development
DOI:10.1016/S1876-3804(16)30129-X URL [Cited within: 2]
Characteristics and EOR mechanisms of nanofluids permeation flooding for tight oil
Laminar forced convection heat transfer of nanofluids inside non-circular ducts: A review
DOI:10.1016/j.powtec.2020.10.042 URL [Cited within: 1]
Effects of non-uniform suction, heat generation/absorption and chemical reaction with activation energy on MHD Falkner-Skan flow of tangent hyperbolic nanofluid over a stretching/shrinking edge
TORSæTER O. A coreflood investigation of nanofluid enhanced oil recovery
DOI:10.1016/j.petrol.2013.07.003 URL [Cited within: 2]
Experimental investigation of SiO2 nanoparticles on enhanced oil recovery of carbonate reservoirs
DOI:10.1007/s13202-014-0120-3 URL [Cited within: 1]
Core flooding of complex nanoscale colloidal dispersions for enhanced oil recovery by in situ formation of stable oil-in-water pickering emulsions
DOI:10.1021/acs.energyfuels.5b02806 URL [Cited within: 2]
Enhanced oil recovery by flooding with hydrophilic nanoparticles
DOI:10.1016/S1672-2515(07)60232-2 URL [Cited within: 3]
Experimental study and mathematical model of nanoparticle transport in porous media
DOI:10.1016/j.powtec.2008.12.017 URL [Cited within: 1]
Modeling and simulation of nanoparticle transport in multiphase flows in porous media: CO2 sequestration
An iterative implicit scheme for nanoparticles transport with two-phase flow in porous media
DOI:10.1016/j.procs.2016.05.423 URL [Cited within: 1]
A numerical investigation of enhanced oil recovery using hydrophilic nanofluids
DOI:10.7569/JSEE.2017.629505 URL [Cited within: 1]
Experimental study and numerical modeling for enhancing oil recovery from carbonate reservoirs by nanoparticle flooding. Oil & Gas Science Technology-Revue de
Transport study of nanoparticles for oilfield application
Crosswell magnetic sensing of superparamagnetic nanoparticles for subsurface applications
DOI:10.2118/166140-PA URL [Cited within: 2]
Application of CFD to evaluate the pore morphology effect on nanofluid flooding for enhanced oil recovery
DOI:10.1039/C4RA15452E URL [Cited within: 3]
CFD investigation of enhanced extra-heavy oil recovery using metallic nanoparticles/steam injection in a micromodel with random pore distribution
DOI:10.1016/j.petrol.2018.10.051 URL [Cited within: 2]
Micro scale investigation of enhanced oil recovery using nano/bio materials
DOI:10.1016/j.mspro.2015.11.069 URL [Cited within: 1]
CFD simulation of enhanced oil recovery using nanosilica/ supercritical CO2
The effect of nanoparticles on wettability alteration for enhanced oil recovery: Micromodel experimental studies and CFD simulation
DOI:10.1007/s12182-019-0312-z URL [Cited within: 3]
Pore-scale simulation of wettability and interfacial tension effects on flooding process for enhanced oil recovery
DOI:10.1039/C7RA07325A URL [Cited within: 3]
Direct numerical simulations of multiphase flow through porous media
Direct numerical simulation of pore scale particle-water-oil transport in porous media
DOI:10.1016/j.petrol.2019.04.078 URL [Cited within: 2]
Funnel flow of a Navier-Stokes-fluid with potential applications to micropolar media
DOI:10.22190/FUME190401029F URL [Cited within: 3]
Experimental study of nanoparticle size and material effect on the oil wettability characteristics of various rock types
DOI:10.1016/j.molliq.2020.114906 URL [Cited within: 1]
International tables of the surface tension of water
DOI:10.1063/1.555688 URL [Cited within: 1]
Thermophysical properties of glycols and glymes
DOI:10.1021/acs.jced.5b00662 URL [Cited within: 1]
Systematic experimental study of the viscosity of nanofluids
DOI:10.1080/01457632.2019.1685240 URL [Cited within: 1]
Volume of fluid (VOF) method for the dynamics of free boundaries
A continuum method for modeling surface tension
DOI:10.1016/0021-9991(92)90240-Y URL [Cited within: 1]
Numerical algorithm for moving-boundary fluid dynamics problems and its testing
DOI:10.1134/S0965542514100091 URL
Study of flow regimes of viscous immiscible liquids in T-type microchannel
Factors affecting liquid-liquid relative permeabilities of a consolidated porous medium
DOI:10.2118/3039-PA URL [Cited within: 2]
Influence of fluid viscosity, interfacial tension, and flow velocity on residual oil saturation left by waterflood
DOI:10.2118/5050-PA URL [Cited within: 3]
Effect of capillary number and its constituents on two-phase relative permeability curves
DOI:10.2118/12170-PA URL [Cited within: 2]