Introduction
Logging-while-drilling (LWD) and formation evaluation technology are key support technologies of high-precision geosteering drilling. It evaluates the conditions of the drilled formation in real-time through the real-time acquisition of trajectory parameters, geological parameters, and engineering parameters near the drill bit, thereby accurately controlling the drilling tool trajectory to hit the best geological target[1]. Logging-while-drilling technology has obvious effects on distinguishing formation change, determining lithology[2,3,4,5], evaluating mud sand/sand shale content[6], and predicting high-pressure formation[7,8], and can improve the benefit of drilling engineering[9]. However, because the information in real-time data transmission is very limited and difficult to interpret[10], it is of great significance to combine artificial intelligence with the interpretation of logging while drilling to improve the accuracy and efficiency of real- time data processing[11,12,13].
In view of the problems encountered in the interpretation of gamma logging while drilling, we propose a real-time dip interpretation method based on long-term and short-term memory (LSTM) and wavelet transform[14,15,16]. This method first extracts the good horizon features and calculates the dynamic threshold to determine the formation boundary position, then trains the classifier model to screen the actual formation boundary, and finally calculates the relative dip angle and azimuth angle of the formation. The method is described in detail and applied in fields.
1. Interpretation process of azimuth gamma logging while drilling
The pulse signals of drilling fluid transmitted by measurement while drilling (MWD) instruments in real time are decoded to obtain the measurement data of various downhole sensors. And then, coordinate conversion, time-depth conversion and correction of the data are carried out. Finally, the imaging of azimuth gamma is obtained by interpolation of the data. On this basis, the interpretation of azimuth gamma data is carried out, and the process is as follows:
(1) Preliminary division of stratigraphic boundaries. First, to eliminate the subtle and sharp changes in the logging curve caused by random noise that is irrelevant to formation changes[17] and retain the trend characteristics of formation changes, the Lowess (locally weighted regression scatter smoothing method) filtering method is used to filter the azimuth gamma ray (GR) curve. Then, the maximum value points on the logging curve are calculated based on the wavelet transform modulus maximum values, and the Lipschitz index (Lip) is used to characterize the singularity of the maximum points on the logging curve to verify the authenticity of each maximum point to realize preliminary extraction of the layer characteristics of the logging curve.
(2) Calculation of dynamic threshold. According to the characteristics and ranges of different layer sequences on the gamma image, the local thresholds of all layer sequences are calculated with entropy and inter-class difference as the standard.
(3) Stratigraphic identification. According to the local threshold of each sequence, the set of contour points of each sequence is calculated. Taking the set of contour points as the input data, the true and false stratum boundary contours are screened by the LSTM classification model.
(4) Calculation of dip. The non-linear least-squares method is used to fit each set of contour points to a sine curve, and the amplitude, initial phase, angular velocity, and other key information of the sine curve are calculated. The relative dip angle of the formation is calculated by the dip calculation formula, and the true dip angle and azimuth angle of the formation are obtained according to the parameter of well deviation.
2. Key technologies
2.1. Layer feature extraction and dynamic threshold calculation based on wavelet transform
2.1.1. Principle of singularity detection based on wavelet transform
Set the curve function as f(t), and Wf(s,t) is the decomposition of f(t) on the corresponding original wave function ψs(t). s is the scale factor. In practical applications, s=2j(j∈Z)[19] usually, and the choice of scale should be in line with the specific signal, usually j=4 or j=5[20], Wf(s,t) is the convolutional binary wavelet transform of f(t).
Assuming that t0 is the local extreme point of the curve function f(t) at the scale s0, then:
If any point t in a certain neighborhood of t0 satisfies the condition shown in Eq. (2), then t0 is called the modulus maximum point of the wavelet transform, and Wf(s0,t0) is called the modulus maximum value of wavelet transform.
The singular value of the curve function f(t) is calculated based on the wavelet transform modulus maximum value, and the singularity of f(t) at a certain point is characterized by the Lip index. If the curve function f(t) is continuous and differentiable at a certain point, the derivative is bounded and discontinuous, then the Lip index of the point is 1, and the point has no singularity; if f(t) is discontinuous but has boundary, the Lip index of the point is 0, and the point has singularity. The sharpness of f(t) at a certain point increases with the decrease of the Lip index. By calculating the Lip index, the singularity degree of a certain point on f(t) can be known, which can assist in checking the mutation characteristic of the maximum points of the curve.
2.1.2. Horizon feature extraction and threshold calculation
The process of the layer feature extraction and dynamic threshold calculation method based on wavelet transform is as follows: firstly the curve of gamma logging while drilling is filtered, then the sequences of the GR curve are divided according to the wavelet transform modulus maximum values and Lip index, and finally the local threshold is calculated according to the result of dynamic division.
2.1.2.1. Influence and filtering of noise in logging curve
The purpose of smoothing the GR curve is to highlight the great changes in lithology of different layers and weaken the subtle changes in lithology within the same layer, avoid the phenomenon of small-diameter wave crests in the curve caused by the statistical fluctuations of the radioactivity measurement of the gamma logging tool, external interference during data transmission, and gamma fluctuations in the same layer lithology[17] and make the mutation positions of the logging curve for horizon extraction more distinct.
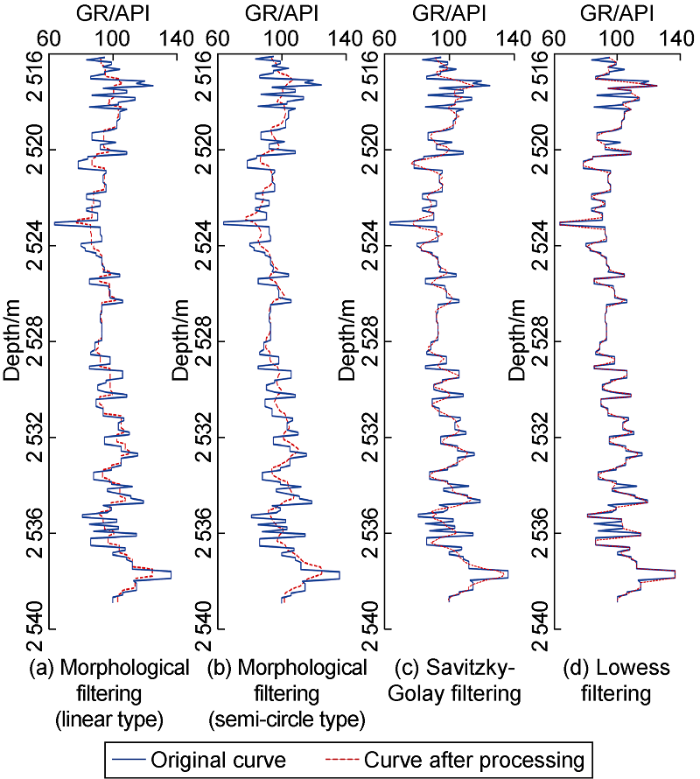
The Lowess filtering method is used to filter the azimuth GR curve, and the basic idea is introduced in reference [21]. Taking the curve of average gamma as an example, the results of smoothing the logging curve by different filtering methods are shown in Fig. 1. Fig. 1 shows that compared with linear morphological filtering and semicircular morphological filtering, Lowess filtering will not lose important curve mutation features; and compared with Savitzky-Golay filtering, the positions with important mutation features retained by Lowess filtering are more consistent with the shape of the original curve.
Fig. 1.
Fig. 1.
Comparison of filtering effects.
2.1.2.2. Sequence division of logging curve
Based on the curve of average gamma after Lowess filtering, the wavelet transform modulus maximum value is used to calculate the singularity, and the Lip index is used to detect the singularity of the points on the curve. Mutation points on the curve are easily detected as singular points, and the locations of the abrupt changes often represent possible stratigraphic changes, as shown in Fig. 2. Therefore, the depths of the formation changes can be located based on the wavelet transform modulus maximum values, which can be used as the basis of calculating the local threshold and the contour points of the formation boundary.
Fig. 2.
Fig. 2.
Diagram of relationship between curve and stratigraphic change.
In light of the characteristics of logging images and the law of stratum distribution, for the stratigraphic boundary point a0, if there are no other boundary points in [a0-C, a0+C], the calculation range of local threshold for a0 is [a0-C, a0+C]; if there are other boundary points in [a0-C, a0] (set the nearest boundary point as a1), and there are no other boundary points in [a0, a0+C], then the calculation range of local threshold for a0 is [(a0-a1)ρ, a0+C]; if there are no other boundary points in [a0-C, a0], but other boundary points in [a0, a0+C] (set a2 as the nearest boundary point), then the calculation range of the local threshold of a0 is [a0-C, (a2-a0)ρ]; if there are other boundary points in both [a0-C, a0] and [a0, a0+C] (set a1 and a2 as the nearest boundary points in two intervals), then the local threshold calculation range of a0 is [(a0-a1)ρ, (a2-a0)ρ]. Among them, C=δ(D+2H)/λ, it is a constant and determines the maximum range of the boundary point a0 when searching for other boundary points. The parameters of δ and ρ are related to the division range when there are no boundary points and there are boundary points. According to the sinusoidal amplitude law of the relative dip angle in the gamma imaging, the values of δ and ρ were respectively set at 20 and 0.85 in this study. H is the imaging depth of the gamma image, which is calculated according to Reference [22] and treated as a constant, and was set at 0.035 m in this study.
According to the boundary points and calculation ranges of their local thresholds, the gamma imaging data can be divided into different layer sequences, and then the local threshold value of each layer sequence can be calculated.
2.1.2.3. The calculation of local threshold
The entropy and inter-class difference are used as indicators to measure the threshold[13]. This indicator comprehensively considers the characteristics of class cohesion and inter-class dispersion. The calculation method of local threshold isn’t elaborated here due to space limit.
2.2. Stratigraphic identification model based on LSTM
The stratigraphic sequences calculated by the extraction of layer features are affected by the curve shape, filtering, algorithm effect, and other factors, which inevitably lead to the extraction of unreal strata, so it is necessary to screen the sequences again. With memory gate structure, the LSTM model is more suitable for solving problems with sequence characteristics[23] and has a wide range of applications in a variety of scenarios[24,25]. The contour data of strata has sequence characteristics, so the LSTM model is used as a classifier of stratigraphic identification.
2.2.1. Classifier design of stratigraphic identification
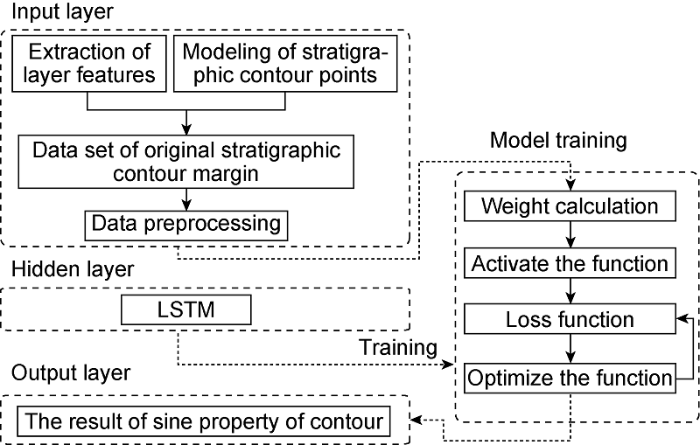
The intersection of the wellbore and the formation boundary is reflected on the gamma image as a curve with sinusoidal characteristic. The screening of a set of contour points can be abstracted as a binary classification of the sine feature in the LSTM network. According to the characteristics of some points in the contour point set and the LSTM design principle, the stratigraphic identification classifier model is constructed as shown in Fig. 3.
Fig. 3.
Fig. 3.
Stratigraphic identification classifier model based on LSTM.
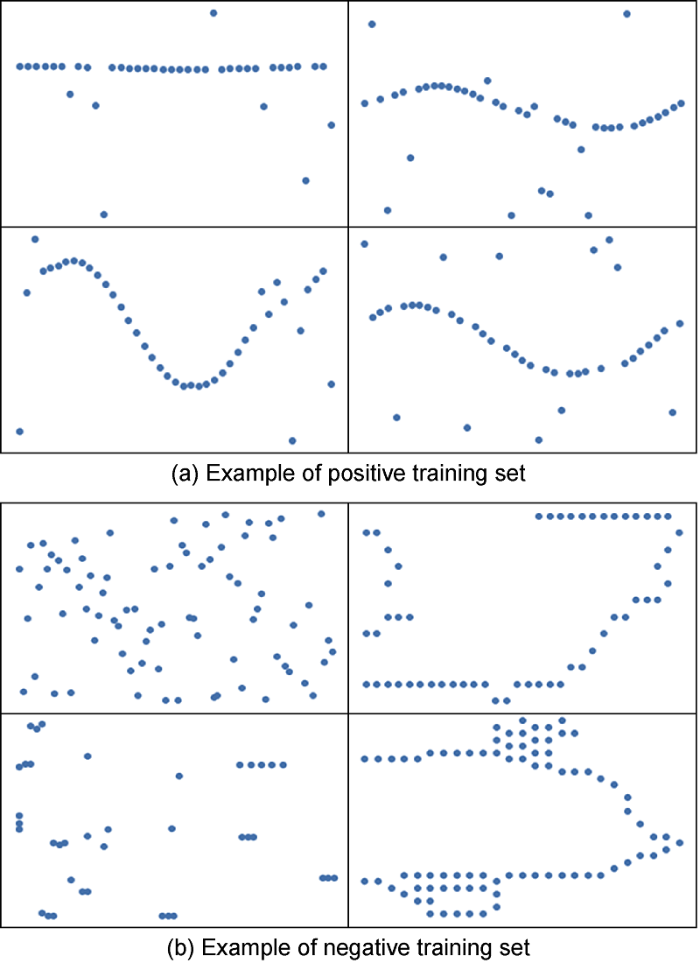
The training set consists of two parts: one part is the sample data, which is interpreted and annotated by artificial log; the other part is the sample data generated by computer according to the characteristics of the formation boundaries. It is defined that, the positive sample is a set of boundary points with sine characteristic, and the negative sample is a set of points without sine characteristic. The training set contains a total of 300 groups of positive samples and 300 groups of negative samples. The number of data points in each group is N (N∈[50, 100]). The range of N is related to the interpolation of azimuth gamma during the preprocessing of gamma image. It can be seen from the results of subsequent classification that the expected accuracy can be achieved by setting the sample size to 600 groups. When designing the training data for positive samples, the characteristics of the sinusoidal curve and stratum edge should be considered. An example of the training data set generated on this basis is shown in Fig. 4. The final output of the model is labeled as 1 or 0, which respectively indicates the presence and absence of the sine feature.
Fig. 4.
Fig. 4.
Example of training data set.
The choice of neurons in the hidden layer of the LSTM model has a greater impact on the training results. The number of neurons is usually determined according to the empirical formula[26] below:
Here, the cross-entropy function is used as the loss function to calculate the error between the result of the classifier and the sample label. Training is carried out through error back-propagation. After the cross-entropy changes stabilize, the Adam gradient optimization algorithm is used to continue the adjustment. Compared with other gradient optimizers, the Adam optimizer is more effective in the actual training of the LSTM model[27].
2.2.2. Model validation and analysis
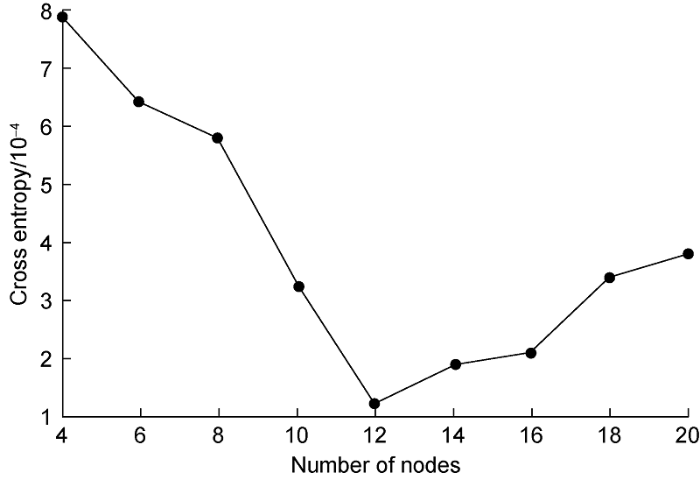
Different numbers of neuron nodes in the hidden layer of the LSTM model were set combined with Eq. (3), the cross-entropy values of different neuron nodes were compared, and the number of nodes with the smallest error was selected as the parameter of the stratigraphic classifier. The cross-entropy values of different neuron nodes are shown in Fig. 5.
Fig. 5.
Fig. 5.
Cross entropy of different numbers of neurons.
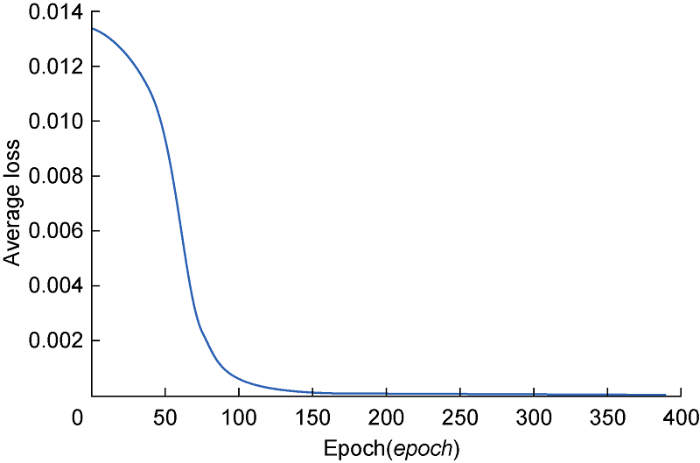
It can be seen from Fig. 5 that the training effect is the best when the number of nodes is 12, and the effect is poor when the numbers of nodes are 4, 6, and 8. The number of neuron nodes in the hidden layer was set at 12 in this study, and the training result of the stratigraphic identification classifier model is shown in Fig. 6. The model training converges around epoch=80, and the average loss value drops to about 1.2×10-4 when epoch=120. The average loss value of the model test set is about 2.3×10-4. The results show that the model can correctly classify the contour points with and without sinusoidal characteristics.
In practice, the local threshold of each layer needs to be calculated firstly, and then the set of contour points in each sequence are obtained. Assuming that the threshold in a sequence is th1, all the data points in the sequence should be checked. If f(xi,yi)=th1, then the position (xi,yi) is marked as a contour point; if the signs of f(xi,yi)-th1 and f(xi+1,yi)-th1 are opposite, the data point with smaller result in them will also be marked as a contour point. Similarly, the contour-point sets of all the layers are calculated and saved to the boundary set. The boundary set is composed of contour point sets. And then the stratigraphic identification classifier model is used to check the sine feature of each contour-point set in the boundary set to remove the contour point sets without sine feature, so the boundary set can reflect the actual formation boundaries.
Fig. 6.
Fig. 6.
Convergence curve of the model.
The above method was used to screen 18 sets of contour points at a certain depth, and the results are shown in Table 1. The results show that the stratigraphic identification classifier based on LSTM after training has the ability to discriminate true and false boundaries between formations.
Table 1 Identification results of contour point sets.
| No. | Contour points | Result | No. | Contour points | Result |
|---|---|---|---|---|---|
| 1 |  | False | 10 |  | False |
| 2 |  | False | 11 |  | True |
| 3 |  | False | 12 |  | True |
| 4 |  | True | 13 |  | True |
| 5 |  | True | 14 |  | True |
| 6 | 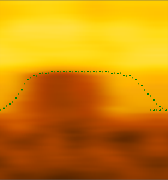 | True | 15 |  | False |
| 7 |  | False | 16 |  | False |
| 8 |  | True | 17 |  | True |

2.3. Calculation of dip
Sinusoidal fitting is performed on the selected contour point sets in the boundary set, to obtain the sine information corresponding to the contour of the formation boundary. The fitting method looking for the local minimum of the function through repeated iterations combined with nonlinear least-squares method, so that the objective function can obtain the optimal solution. Finally, according to the sine information from fitting (Eq. (4)) and the method in Reference [17], the relative dip and azimuth angle of the formation are calculated. The formulas are Eqs. (5) and (6) respectively. See the relevant reference for the derivation process.
3. Method validation and application
In order to verify the feasibility and accuracy of the method presented in this paper, the application and analysis were carried out from two aspects: azimuth- gamma interpretation and real-time data processing while drilling.
3.1. Interpretation of azimuth gamma data
The experimental data is 8-channel azimuth gamma data of 2100 m to 2380 m depth in Well X in China. The azimuth gamma data of the well was well pre-processed and clear in image. By comparing with the results of manual interpretation, the validity and accuracy of the method in this paper in stratigraphic identification and dip angle calculation could be verified.
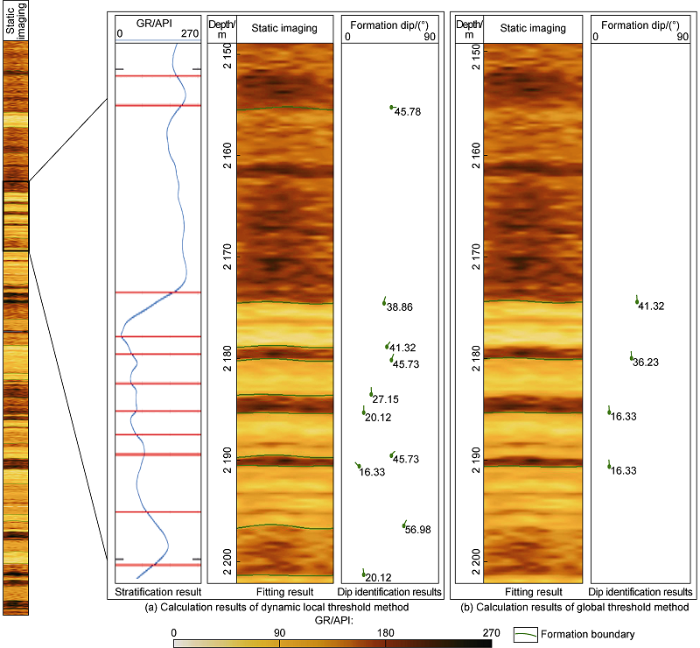
The results of stratigraphic identification, fitting, dip calculation and those of global-threshold method[13] are shown in Fig. 7. It can be seen that the method in this paper has better effects in stratigraphic identification and contour fitting, and can more accurately describe the changes and the boundary contour curves of formations. Compared with the global threshold method, this new method can interpret more formation dip angles. The comparison of formation dip results of local well section from this method and manual interpretation is shown in Table 2. It can be seen that the interpretation result of the new method is close to the manual interpretation result. The well section is 280 m long with 22 400 measurement points. The number of layers from manual interpretation was 50, and the number of layers interpreted by the new method was 46. For longer well sections with more measurement points, the method presented in this paper has a stratigraphic identification rate of 92% and accuracy of dip calculation of 96.6%, proving that the new method is quite accurate.
Fig. 7.
Fig. 7.
Comparison of the results from the method in this paper and global threshold method.
Table 2 Comparison of results of actual azimuth gamma data from this method and manual interpretation.
| Depth/ m | Interpretation results of the method in this paper/(°) | Results of manual interpretation/(°) | Absolute error/(°) |
|---|---|---|---|
| 2 155.0 | 45.73 | 45.13 | 0.60 |
| 2 174.4 | 38.86 | 38.88 | 0.02 |
| 2 178.7 | 41.32 | 41.12 | 0.20 |
| 2 180.0 | 45.72 | 45.70 | 0.02 |
| 2 183.4 | 27.15 | 26.68 | 0.47 |
| 2 185.2 | 20.12 | 20.14 | 0.02 |
| 2 189.4 | 45.73 | 45.72 | 0.01 |
| 2 190.5 | 16.33 | 16.02 | 0.31 |
| 2 196.3 | 56.98 | 57.79 | 0.81 |
| 2 201.2 | 20.12 | 20.12 | 0 |
3.2. Real-time data processing while drilling
Well Y is horizontal well in an oilfield in eastern China. It was drilled to tap the remaining oil in high position of a thin reservoir, further increase the reserves producing degree, and improve the development effect. Its geo-steering service adopted a new type of geo-steering system composed of a domestically-developed near-bit geo-steering system + azimuth gamma while drilling + integrated measurement-while-drilling interpretation system. The well section of geosteering technology service started in front of target A at 2184 m depth to the completed well at depth of 3075 m, with a cumulative footage of 891 m, and took 82 h. The system not only realized the upload of conventional MWD (measurement while drilling) trajectory and attitude measurement parameters, including deviation, azimuth, tool face, and temperature, but also uploaded the near-bit deviation and two gamma (up and down) logs in real-time, which provided a timely and accurate decision-making basis for real-time geological guidance.
The data of this well was used to verify the effect of the method in this paper on interpolation imaging and formation boundary interpretation during real-time drilling. The processing result of this method in this case is shown in Fig. 8. It can be seen that the method obtained clear image of real-time gamma data based on data interpolation; the stratigraphic division by the method based on stratigraphic division and local threshold calculation tallies with the actual situation; and accurate stratigraphic boundaries based on the LSTM classifier model. Especially at the depth of 2440-2450 m in Fig. 8, the classifier model screened out several sets of contour points without sinusoidal features, and the contour points were fitted to the correct positions by the fast sine fitting method. It can be seen from Table 3 that the new method has high accuracy in processing real-time data, and the interpretation results are close to that of manual interpretation. The interpretation time of this section by the new method was about 0.27 s, which is much more efficient than manual interpretation. The analysis of the results shown in Fig. 8 and Table 3 proves that the new method is effective in actual production.
The above calculation results and analysis show that the method in this paper has high accuracy and faster computation speed in automatic stratigraphic identification, and can process real-time LWD data. In practical application, near-bit well inclination measurement is used to ensure the landing of well trajectory into the target and extending along the target. The azimuth gamma data and resistivity data near the bit are processed to judge the horizon being drilled and ensure the drilling rate of target layer.
4. Conclusions
Compared with the global threshold method and fixed threshold method, the dynamic threshold method based on wavelet transform significantly improves the accuracy of formation interface interpretation. When the formation lithology is stable, this method reduces useless calculation, and is also suitable for the situation with rapid changes in the geological structure.
The formation boundary classifier model based on the characteristics of gamma data while drilling was designed by using LSTM, and the feature data set of formation boundaries was established. In the training process, parameters such as the number of neuron nodes and learning rate were adjusted to avoid over/under fitting. Comparison shows that the classifier model can accurately identify the contour with sinusoidal feature and screen out the real formation boundary.
The LWD interpretation method based on artificial intelligence can assist the decision-making of drilling engineers, and provide technical support for real-time geo-steering.
Fig. 8
Fig. 8
Interpretation results of real-time data while drilling at the well site.
Table 3 Comparison of the interpretation results of the formation dip obtained after the interpretation of the real-time data while drilling using the method in this article and the manual method.
| Depth/ m | Interpretation results of the method in this paper/(°) | Results of manual interpretation/(°) | Absolute error/(°) |
|---|---|---|---|
| 2 392.7 | 52.83 | 57.76 | 4.93 |
| 2 395.9 | 60.37 | 58.87 | 1.50 |
| 2 400.4 | 75.29 | 74.40 | 0.89 |
| 2 402.6 | 78.97 | 78.98 | 0.01 |
| 2 418.7 | 75.02 | 74.43 | 0.59 |
| 2 426.0 | 74.13 | 74.44 | 0.31 |
| 2 439.3 | 51.23 | 50.29 | 0.94 |
| 2 445.3 | 69.23 | 70.45 | 1.22 |
| 2 447.5 | 72.38 | ||
| 2 450.2 | 56.98 | 56.45 | 0.53 |
| 2 452.8 | 79.11 | 76.02 | 3.09 |
Nomenclature
a0, a1, a2—stratification points, that is the positions of wavelet transform modulus maximum values in the step of the layer extraction;
A—amplitude;
D—diameter of borehole, m;
f(·)—curve function;
H—imaging depth of gamma image, m;
i—the serial number of the points on the curve;
j—coefficient related to scale factor;
K—constant, K∈[0,10];
m, n—the number of nodes in input layer and output layer;
M—the number of neurons;
N—the number of data points in each group of samples;
s—scale factor;
th1—the local threshold of a sequence;
t—a point on the curve f(t);
t0—the local extremum of the curve function f(t) under the scale of s0;
Wf(s,t)—the decomposition of f(t) on the corresponding original wave function ψs(t);
x—x-axis coordinate, m;
xi, yi—coordinates of a point on the curve, m;
y0—offset, m;
Z—set of integers;
α, β—relative dip angle and azimuth angle of the stratum, (°);
δ—parameters related to the division range when there are no stratification points above and below;
λ—distance between measuring points of logging tool, m;
ρ—parameters related to the division range when there are stratification points above and below;
φ—primary phase;
ψs(t)—original wave function;
ω—angular velocity.
Reference
Well optimization using a LWD spectral azimuthal gamma ray tool in unconventional reservoirs
A method for calculating more accurate stratigraphic positioning of horizontal wells using continuous inclination and azimuthal gamma ray images even while sliding.
Tool design of look-ahead electromagnetic resistivity LWD for boundary identification in anisotropic formation
DOI:10.1016/j.petrol.2019.106537 URL [Cited within: 1]
Comparison and application of neural networks in LWD lithology identification
DOI:10.1088/1755-1315/526/1/012146 URL [Cited within: 1]
Real-time downhole data resolves lithology related drilling behavior.
Laminated sand shale formation evaluation using azimuthal LWD resistivity.
Application of formation pressure prediction while drilling technology in HTHP wells
Enhancing performance and operational safety of Argentinean Vaca Muerta shale wells by drilling high pressure formations using managed pressure drilling.
Optimizing a unique new generation LWD technology for petrophysical evaluation, well-placement, geological mapping and completion design: Carbonate reservoir case study.
Real-time azimuthal gamma and resistivity LWD data used to navigate complex unconventional reservoir: Western US Land.
A deep- learning approach for borehole image interpretation.
Optimizing horizontal well placement through stratigraphic performance prediction using artificial intelligence
Formation lithology classification: Insights into machine learning methods
The study on composite load model structure of artificial neural network
Automatic slicing method of logging curves based on morphological filtering and wavelet transform
Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network
Research and application of data processing method of gamma ray measurement while drilling
A new image enhancement algorithm based on wavelet transform
Research on wavelet transform modulus maximum denoising algorithm
Signal singularity detection based on modulus maxima of wavelet transform
Smoothing reference centile curves: The LMS method and penalized likelihood
DOI:10.1002/(ISSN)1097-0258 URL
Quantitative study of natural gamma ray depth of image and dip angle calculations. New Orleans,
Gas data prediction based on LSTM neural network
Skeleton-based human action recognition with global context-aware attention LSTM networks
DOI:10.1109/TIP.2017.2785279 URL [Cited within: 1]
Ship track prediction model based on LSTM
Fault time series prediction based on LSTM recurrent neural network