Introduction
In volatile oil reservoirs, the gas/oil ratio usually ranges from 267 to 623 m3/m3, and the oil volume factor is greater than 1.8. In the volatile oil reservoir, the oil is highly shrinkable below bubble point pressure. It is generally believed that if production by natural depletion, the recovery factor in the volatile oil reservoir is low, ranging from 19% to 25%[1]. In order to avoid oil shrinkage, during the development of the volatile oil reservoirs, water injection or gas injection pressure-maintaining production or miscible flooding production methods are applicable. A number of field results show that during the production of the volatile oil reservoirs, the oil recovery factor by pressure depletion production is higher than expected. Buck Draw field in the United States is an oil field with weak oil volatility. It was put into production in 1978, and oil production decline was not seriously when production was conducted below bubble point pressure. Li et al.[2] believe that the condensate oil contained in free gas might cause the delay of production decline. The oil field BZ13-1, located in Bohai Bay, was originally under saturated. Limited by offshore platform, this field was developed by pressure depletion. During the production, the gas-oil ratio increased steadily. When the reservoir formation pressure dropped by 40%, the oil recovery factor reached 22%[3], which exceeded the expectation value. The field ZH1-2L is located at the west coast of South China Sea, and the gas-oil ratio did not show increasing trend when production was conducted below bubble point pressure. When reservoir pressure dropped by 35%, the oil recovery factor reached 20%[4]. These field cases suggest that with the traditional prediction methods of the oil recovery factor from the volatile oil reservoirs, there might be some problems.
In oil reservoirs developed by pressure depletion production, the recovery factor is predicted based on the conventional solution-gas drive theory, such as the widely used Muskat[5], Schilthus[6] and Tarner[7] methods. When using these methods, it is assumed that oil and gas phases exist in the reservoir, and mass transfer does not take place between oil and gas phases. In fact, due to high percentage of middle composition in volatile oil, mass transfer will happen during production by pressure depletion. Therefore, the prediction method on the ultimate recovery factor based on traditional solution-gas drive theory should be improved. Researches on the recovery factor in the volatile oil reservoir started in 1974, Cook et al.[8] and Coats[9] proposed the concept of the volatile oil -gas ratio, which can be measured by constant volume depletion experiment for volatile oil. In 1986, Fetkovich and Lu et al.[10,11] applied the concept of volatile oil-gas ratio, and derived the equation for calculation of oil and gas relative permeability ratio from the volatile oil reservoir or condensate gas reservoir. In 1994, Walsh et al.[12,13] conducted further derivation of general material balance equation. Previous study results have laid a certain foundation for the prediction of oil recovery factor from the volatile oil reservoirs, but systematic study approaches have not been established yet.
The physical parameters of crude oil measured by multiple degassing experiment cannot be used directly for prediction of oil recovery factor from the volatile oil reservoirs. The specific reasons are: (1) Tuo et al.[14-16] pointed out that multiple degassing experiment is based on the assumption that oil and gas are in equilibrium state, and there is no mass transfer. However, this experimental principle does not apply to the volatile oil reservoir. (2) Wu et al.[17,18,19] believed that during the process of single degassing or multiple degassing experiment, large pressure drop rate and pressure drop range might occur, causing unbalanced oil and gas separation, resulting in experimental data error. (3) In regard to experiment data error due to the experimental principle, Lu et al.[20] proposed an approach to correct multiple degassing experimental data using constant volume depletion experimental data, and also proposed correcting equation.
In order to describe the complex phase behaviors during the production of volatile oil reservoir, 4 reservoir fluid phases are defined in this study (liquid oil, liquid gas, free gas, and condensate oil). In addition, according to material balance at surface, the separation of production rate and remaining reserve are realized for each phase. Therefore, the influence of the condensate oil from solution gas was taken into account, and the traditional methods based on solution-gas drive theory for prediction of the oil recovery factor in the volatile oil reservoir were improved. Combined with single degassing, multiple degassing and constant volume depletion experiments, correction methods for multiple degassing experiment data have been established.
1. Limitation of conventional reservoir engineering methods
1.1. Limitation of multiple degassing experiment
One oil sample was selected for each well from the following wells, namely BZ13-2 of BZ13-1 field, BZ13-1-A4 of BZ13-1 field, NB19-6-2 in WYT Structure of East China Sea, Akpo-2 of Akpo field in West Africa, CX-4 of CX field in East China Sea, and PVT characteristics of the 5 samples were summarized in Table 1. As indicated by Table 1, the various parameters for each sample are correlated. The higher the solution gas-oil ratio from single degassing experiment, the greater the oil volume factor, and also the higher of the solution gas-oil ratio from multiple degassing experiment. Using solution gas-oil ratio from single degassing experiment as basis, the 5 samples are defined as strong volatile oil reservoir (Sample 1, 2), medium-to-weak volatile oil reservoir (Sample 3, 4) and typical black oil (Sample 5) respectively, and the experiment temperature are 166, 166, 119, 85, 110oC respectively. In general, the more volatile the oil sample is, the greater the difference of oil volume factor and solution gas-oil ratio measured from single degassing and multiple degassing experiments, and the more the volume of condensate oil from constant volume depletion experiment.
Table 1 PVT characteristics of the experiment for typical oil.
| Sample | Pressure/ MPa | Several degassing | Constant Volume Depletion | Single degassing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Solution GOR/ (m3·m-3) | Oil FVF | Liquid viscosity/ (mPa·s) | Gas viscosity/ (mPa·s) | Condensate- gas ratio/ (cm3·m-3) | Gas FVF | Liquid saturation/ % | Solution GOR/ (m3·m-3) | Oil FVF | ||
| 1 | 40.51 | 1 093 | 5.230 5 | 0.057 0 | 100.00 | 761.10 | 3.662 8 | |||
| 34.32 | 336 | 2.123 5 | 0.125 0 | 0.025 9 | 502 | 0.004 690 | 45.81 | |||
| 28.48 | 240 | 1.979 5 | 0.175 0 | 0.023 9 | 379 | 0.005 240 | 36.74 | |||
| 22.56 | 169 | 1.787 1 | 0.218 0 | 0.021 1 | 295 | 0.006 220 | 33.52 | |||
| 16.75 | 116 | 1.630 0 | 0.258 0 | 0.017 7 | 252 | 0.008 190 | 28.43 | |||
| 9.83 | 66 | 1.487 1 | 0.306 0 | 0.016 2 | 231 | 0.013 980 | 25.03 | |||
| 2 | 40.02 | 763 | 3.660 0 | 0.063 0 | 100.00 | 563.42 | 2.710 6 | |||
| 35.00 | 363 | 2.280 0 | 0.110 9 | 0.034 9 | 525 | 0.004 604 | 64.51 | |||
| 30.00 | 232 | 1.820 0 | 0.153 1 | 0.028 8 | 423 | 0.005 068 | 50.46 | |||
| 25.00 | 159 | 1.590 0 | 0.194 5 | 0.024 5 | 349 | 0.005 877 | 44.63 | |||
| 20.00 | 110 | 1.430 0 | 0.240 1 | 0.021 7 | 292 | 0.007 178 | 42.05 | |||
| 15.00 | 73 | 1.320 0 | 0.294 6 | 0.019 7 | 247 | 0.009 454 | 40.07 | |||
| 10.00 | 44 | 1.230 0 | 0.363 1 | 0.018 1 | 214 | 0.014 219 | 36.11 | |||
| 3 | 32.39 | 518 | 2.754 0 | 0.133 3 | 0.031 5 | 100.00 | 448.21 | 2.391 4 | ||
| 27.57 | 325 | 2.093 0 | 0.173 0 | 0.026 5 | 379 | 0.005 060 | 75.14 | |||
| 24.81 | 267 | 1.905 0 | 0.196 1 | 0.024 4 | 324 | 0.005 450 | 69.21 | |||
| 20.67 | 198 | 1.686 0 | 0.233 5 | 0.022 0 | 260 | 0.006 320 | 63.28 | |||
| 16.53 | 148 | 1.534 0 | 0.276 7 | 0.020 2 | 216 | 0.007 750 | 57.24 | |||
| 12.40 | 108 | 1.413 0 | 0.328 2 | 0.018 9 | 193 | 0.010 210 | 53.55 | |||
| 8.26 | 72 | 1.305 0 | 0.391 1 | 0.017 6 | 190 | 0.015 100 | 49.34 | |||
| 4 | 30.72 | 345 | 2.000 0 | 0.150 7 | 100.00 | 319.65 | 1.840 2 | |||
| 27.64 | 271 | 1.820 0 | 0.172 2 | 0.026 6 | 346 | 0.004 130 | 90.50 | |||
| 25.06 | 234 | 1.680 0 | 0.192 8 | 0.024 7 | 308 | 0.004 450 | 85.11 | |||
| 17.89 | 158 | 1.490 0 | 0.262 6 | 0.020 6 | 230 | 0.006 030 | 74.06 | |||
| 11.94 | 105 | 1.360 0 | 0.334 6 | 0.018 7 | 199 | 0.009 140 | 69.20 | |||
| 4.71 | 48 | 1.220 0 | 0.439 3 | 0.018 1 | 197 | 0.024 530 | 63.43 | |||
| 5 | 26.55 | 159 | 1.500 0 | 0.160 0 | 100.00 | 156.37 | 1.484 3 | |||
| 20.00 | 126 | 1.450 0 | 0.210 0 | 0.015 0 | 76 | 0.006 210 | 96.82 | |||
| 15.00 | 93 | 1.410 0 | 0.270 0 | 0.014 8 | 48 | 0.008 160 | 94.09 | |||
| 10.00 | 61 | 1.350 0 | 0.360 0 | 0.014 5 | 31 | 0.012 140 | 90.05 | |||
| 5.00 | 30 | 1.250 0 | 0.540 0 | 0.014 1 | 22 | 0.024 240 | 83.42 | |||
In single degassing experiment, there is no oil loss because all fluid is in PVT cell all the time. In multiple degassing experiment, the condensate oil in the dissolved gas is expelled out of PVT cell together with free gas, and is not included in ultimate recovered oil volume. Therefore, when equilibrium is achieved in experiment under saturation pressure, gas-oil ratio from multiple degassing experiment will be higher than that from single degassing experiment. In actual reservoir production, the condensate oil from the expelled dissolved gas is partly recovered together with free gas, partly vaporized into condensate oil again, and partly remained in reservoir. The results of multiple degassing experiment cannot be straightly applied in prediction of oil recovery factor from the volatile oil reservoirs, and the experiment data needed to be corrected.
1.2. Limitation of the conventional solution-gas drive theory
For the closed oil reservoir with abandon pressure higher than bubble point pressure, there will be no dissolved gas escaping from the formation during production, and the ultimate recovery factor can be calculated by material balance of undersaturated oil reservoir based on oil expansion[21]:
For saturated oil reservoir, due to gas released from oil during production, the ultimate recovery factor is estimated by conventional solution-gas drive theory, which includes 3 basic equations. They are material balance equation of conventional solution-gas drive reservoir, oil saturation prediction equation and instantaneous producing gas-oil ratio prediction equation, presented by Eq. (2-5)
The cumulative gas-oil prediction equation is
Combing Eq. (2), Eq. (3) and Eq. (5) and conducting iteration, with cumulative gas-oil ratio prediction equation as objective, gives prediction of oil saturation.
In the equations of conventional solution-gas drive, there is no condensate oil content in gas phase, indicating that gas released from oil is dry gas. This is not consistent with the fact that there is condensate oil in the dissolved gas extracted from the PVT constant volume depletion experiment of volatile oil. If application of this theory to predict the recovery factor from the volatile oil reservoir, the recovery factor will be underestimated. Therefore, the calculation method needs to be improved. When predicting the oil recovery factor from volatile oil reservoirs with conventional reservoir engineering method, it is necessary to correct the multiple degassing experiment data, and the conventional solution-gas drive theory needs to be improved. The condensate oil contained in dissolved gas should be taken into account.
2. Improvement in the method for prediction of oil recovery factor
Considering the influence of condensate oil content in dissolved gas escaped from volatile oil reservoir on the ultimate oil recovery factor, studies have been conducted in terms of calculation method and experiment data correction. Three basic equations of conventional solution-gas drive theory have been improved, and equation for correcting multiple degassing experiment data has been established.
2.1. Separation of remaining volume and production for each fluid phase
With the production of the volatile oil reservoir, at the time when the formation pressure is below bubble point pressure, the residual hydrocarbon fluid in the reservoir fluid will be transformed from single oil phase into coexisting of free oil phase and free gas phase. In addition, there is solution gas in free oil phase, and condensate oil in free gas phase. Therefore, the produced oil at surface consists of the oil and gas from reservoir, so does the produced gas. In order to clearly describe the phase transformation of reservoir fluids at surface, 4 reservoir fluid phases were defined: liquid oil, liquid gas, free gas, and condensate oil. Liquid oil and liquid gas exist as oil phase in reservoir, while be transformed into oil phase and gas phase at surface; free gas and condensate oil exist as gas in reservoir while be transformed into gas and oil at surface. The volume of the 4 phases are defined at standard condition at surface, and according to volume balance at surface remaining volume and production of each phase are calculated.
2.1.1. Calculation of remaining liquid oil volume and remaining free gas volume
At original reservoir condition, only single oil phase exists in reservoir and original liquid oil volume equals original oil in place Vfoi and original liquid volume equals original solution gas in place, expressed as VfoiRsi. When reservoir pressure drops below bubble point pressure two phases coexist in reservoir, which are remaining liquid oil volume expressed as Vfo, remaining free gas volume Vfg, remaining condensate oil expressed as VfoRs and cumulative gas production expressed as VpRps as cumulative oil production is expressed as Vp.
According to oil and gas material balance at surface: the sum of reservoir remaining liquid oil and reservoir remaining condensate oil equaling the difference of original oil in place and cumulative oil production; the sum of reservoir remaining free gas and reservoir remaining liquid gas equaling the difference of the original liquid gas in place and cumulative gas production, it gives
Combing Eq. (6) and Eq. (7) gives the remaining liquid oil and remaining free gas:
2.1.2. Calculation of instantaneous production of gaseous gas and liquid oil
When reservoir pressure drops below bubble point pressure, qfg denotes free gas transient gas rate and qfo denotes liquid oil transient oil rate, and condensate oil transient rate can be expressed as qfgRv and liquid gas transient rate can be expressed as qfoRs. If measured total gas rate in field is qg and qo for oil, according to material balance at surface, we can have
Combining Eq. (10) and Eq. (11) gives liquid oil and free gas transient rate
2.2. Modification of conventional solution-gas drive theory
2.2.1. Material balance equation for the recovery factor from the volatile oil reservoir
When reservoir pressure is below bubble point pressure, the recovery factor in the volatile oil reservoir obeys the volume balance (closed reservoir without consideration of water influx): original pore volume of hydrocarbon is equal to the sum of current pore volume filled with oil phase and gas phase.
Putting Eq. (8) and Eq. (9) into Eq. (14) yields
where
$F={{V}_{p}}\frac{{{B}_{o}}\left( 1-{{R}_{v}}{{R}_{ps}}^{*} \right)+{{B}_{g}}\left( {{R}_{ps}}^{*}-{{R}_{s}} \right)}{1-{{R}_{v}}{{R}_{s}}}$
${{E}_{o}}=\frac{{{B}_{o}}-{{B}_{oi}}+{{B}_{g}}\left( {{R}_{si}}-{{R}_{s}} \right)+{{R}_{v}}\left( {{B}_{oi}}{{R}_{s}}-{{B}_{o}}{{R}_{si}} \right)}{1-{{R}_{s}}{{R}_{v}}}$
Eq. (15) denotes material balance equation of the recovery factor in the volatile oil reservoir with resemblance of conventional material balance equation by Havlena-Odeh[22,23]. The physical meaning of material balance equation is that original oil expansion accounts for the reservoir volume of produced hydrocarbon. The proposed general material balance equation considers the effect of condensate oil and liquid gas while the conventional material balance equation only considers the effect of liquid gas. Putting F into Eq. (15) and solving for oil recovery factor, we have
Eq. (16) has considered condensate oil in solution gas and improved Eq. (2) for oil recovery prediction by conventional solution-gas dry theory.
2.2.2. Equation of oil saturation prediction of the recovery factor from the volatile oil reservoir
Oil saturation can be expressed as pore volume filled with oil divided by total pore volume:
Putting Eq. (17) and Ro*=Vp/Vfoi into Eq. (17) yields
Eq. (18) has considered the effect of condensate oil from solution gas and improved Eq. (3) for oil recovery prediction by conventional solution-gas dry theory.
2.2.3. Equation of producing gas-oil ratio in the volatile oil reservoir
The instantaneous flow rate of the free oil phase in the reservoir should be equal to the instantaneous liquid oil production multiplying oil volume factor, instead of total oil rate converted from the instantaneous total oil production measured in the field, so is free gas. The ratio of Darcy’s equation for gas and oil phase gives
Putting Eq. (12) and Eq. (13) into Eq. (19) and multiplying qo for nominator and denominator at left hand side of the equation, instantaneous producing gas-oil rate (Rgo*=qg/qo) can be written as
Applying integration to Eq. (20) with respect to oil recovery factor leads to cumulative gas production per unit oil reserve, and therefore cumulative gas-oil ratio can be written as
Eq. (21) is the modification of Eq. (5), which is based on conventional solution-gas drive theory, with the consideration of the influence of condensate oil from solution gas.
Eq. (16), Eq. (18) and Eq. (21) constitute the new equations for prediction of oil recovery factor from the volatile oil reservoir. When reservoir fluid PVT characteristics and oil & gas relative permeability curves are given, oil recovery factor can be estimated by iteration with the following 4 steps: 1) given an initial reservoir pressure drop, calculating reservoir fluid characteristics, with assumption of an Rps*, calculating oil recovery factor Ro*; 2) putting oil recovery factor and assumed Rps* both obtained at last step into Eq. (18), solving for So*; 3) reading the Krg/Kro based on So* obtained in Step 2 and relative permeability curves, along with Eq. (21) acquiring cumulative producing gas-oil ratio; 4) comparing the cumulative producing gas-oil ratio by Step 1 and Step 3, iterating the above process until the difference is small. By the same procedures, oil recovery can be estimated at various levels of reservoir pressure drop.
2.3. Multiple degassing experiment data correction
Multiple degassing experiment was conducted at reservoir temperature, at various level of pressure drops. The oil volume remained in PVT cell and gas volume expelled out of PVT cell were measured. Based on the measured data, the PVT physical properties of crude oil were calculated. Due to the fact that the condensate oil contained in expelled gas is not measured, experiment data-based oil volume factor and solution gas-oil ratio was overestimated. However, along with measured condensate oil volume in constant volume depletion experiment, it is possible to calculate real oil formation factor and solution gas-oil ratio according to volume balance at surface.
Set the initial saturation pressure during the multiple degassing experiment as the 0-level pressure, and set the ultimate residual oil volume at standard condition as 1m3, oil volume in PVT cell Vodb numerically equaled to the oil formation factor at corresponding saturation pressure, and oil formation factor at saturation pressure Bob was obtained by single degassing measurement, and liquid oil volume at saturation pressure was
Hence, at j-th pressure oil volume in PVT cell numerically equals oil formation factor measured by differential liberty, which is denoted by Bo,j, and remaining oil volume is
The released gas volume at the j-th pressure Vsd,j-1-Vsd,j numerically equals the difference of solution gas-oil ratio between the (j-1)-th and j-th pressure, and therefore the released condensate oil is Rv,j×(Vsd,j-1-Vsd,j), with the measured condensed oil by constant volume depletion experiment as Rv,j. The cumulative condensate oil released from o to j-th pressure Vp,j can be mathematically described as
Considering the completion of gas releasing at j-th pressure, without gas in the PVT cell Vfg=0, only condensate oil was produced during the process. The oil volume balance at surface should be: the remaining liquid oil volume is equal to the difference of liquid oil volume at saturation pressure and cumulative released condensate oil volume, which is
Subtracting Eq. (22) to Eq. (24) along with Eq. (25), oil volume factor can be obtained
Replacing Vod,j by Vsd,j in Eq. (26), the corrected solution gas-oil ratio is:
3. Field Application
According to the sample data in Table 1, with the proposed experiment data correction method, the oil volume factor and solution gas-oil ratio from multiple degassing experiment were corrected. The proposed modification method of oil recovery factor prediction is applied to simulate the constant volume depletion experiment, in order to validate the proposed modification method. Finally, three prediction methods, namely “experiment data-conventional method”, “corrected experiment data-conventional method” and “corrected experiment data-corrected method” were used respectively to estimate oil recovery factor, to make clear the influence of the condensate oil content contained in solution gas on the oil recovery factor.
3.1. Experiment data correction
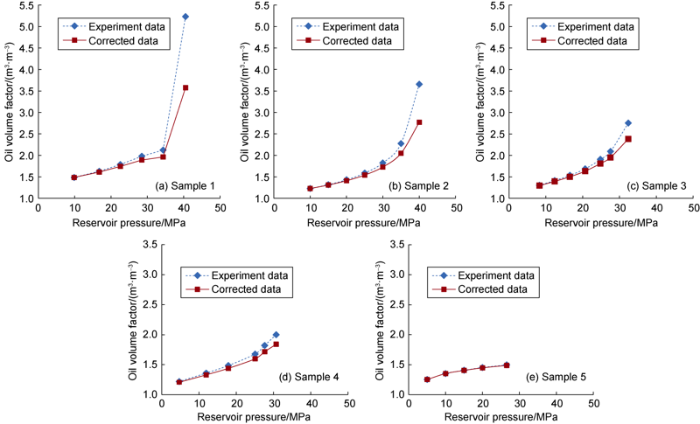
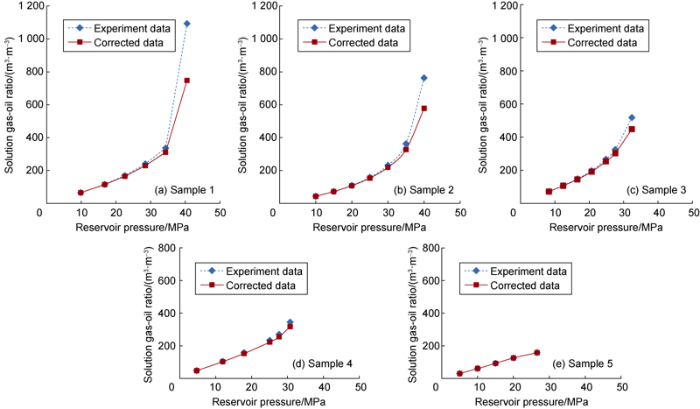
Multiple degassing experiment data was corrected by Eq. (26) and Eq. (27), as shown in Figs. 1 and 2. It can be seen that either oil volume factor or solution gas-oil ratio for typical black oil (Sample 5) barely shows difference before or after correction, while shows apparent difference for weak-to-medium volatile oil reservoir (Sample 3, 4), and the difference is even enlarged for strong volatile oil reservoir (Sample 1, 2). It is suggested by comparison of experiment data that the level of difference of oil volume factor and solution gas-oil ratio before and after data correction is determined by the level of condensate oil contained in solution gas. The more condensate oil in gas phase, the more pronounced the difference for oil volume factor and solution gas-oil ratio before and after data correction.
Fig. 1.
Fig. 1.
Oil volume factor from corrected multiple degassing experiment data.
Fig. 2.
Fig. 2.
Solution gas-oil ratio from corrected multiple degassing experiment data.
3.2. Simulation and method validation
During the PVT constant volume depletion experiment, keep the volume constant, only free gas was expelled out of PVT cell. Therefore, setting Kro=0 and Swi=0 in Eq. (16, 18 and 21), the constant volume depletion experiment can be simulated. For basic experiment fluid parameters, oil volume factor and solution gas-oil ratio were obtained by correction of multiple degassing experiment, and abandon pressure was set as 1/4 of the reservoir pressure.
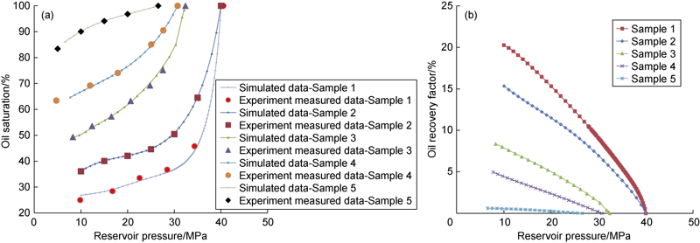
Fig. 3a illustrates the comparison of oil saturation of the 5 samples obtained by proposed method and by experiment measurement. The comparison shows good agreement of the two sets of results, which, to a large extent, validates the proposed method. Fig. 3b illustrates the calculated oil recovery factor of the 5 samples under constant volume depletion condition. It can be seen that even if oil is assumed to be not movable (Kro=0), the ultimate oil recovery factor reaches 20.28%, 15.35% for strong volatile oil reservoir (Sample 1, 2), suggesting the importance of condensate oil contained in dissolved gas produced in volatile reservoirs to oil production.
Fig. 3.
Fig. 3.
Predicted results by improved method of constant volume depletion experiment.
In addition, newly proposed method can be validated by the inheritance of conventional method. Setting Rv=0 in Eq. (16, 18 and 21) gives the same equations, Eq. (2, 3 and 5), as conventional method.
3.3. Comparison of oil recovery factor obtained by different methods
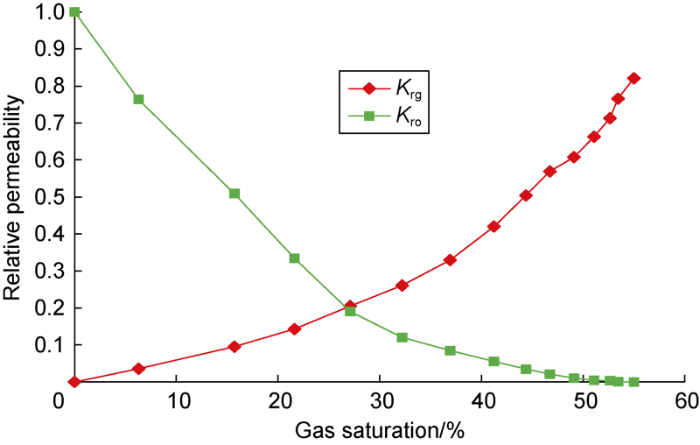
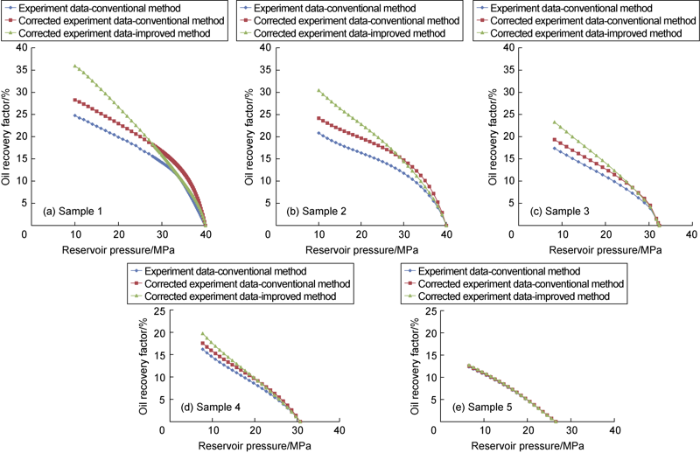
Three methods were used for each oil sample. Method 1: using conventional solution-gas drive theory based on multiple degassing experiment data, named as “experiment data-conventional method”. Method 2: using conventional solution-gas drive theory based on corrected multiple degassing experiment data, named as “corrected experiment data-conventional method”. Method 3: using proposed improved method for oil recovery factor prediction based on corrected multiple degassing experiment data, named as “corrected experiment data-improved method”. All cases use the same relative permeability curves (Fig. 4), and irreducible water saturation was set as 30%, and the abandon pressure was set as 1/4 of the reservoir pressure.
Fig. 4.
Fig. 4.
Oil & gas relative permeability curve.
Fig. 5 presents the oil recovery factor obtained by the three methods versus average reservoir pressure. It can be seen that results obtained by the three method are very close for typical black oil (Fig. 5e), with ultimate oil recovery factor of 12. 34%, 12.52% and 12.74 by “experiment data-conventional method”, “corrected experiment data-conventional method”, “corrected experiment data- improved method” respectively. Results obtained by three methods for weak-to-medium volatile oil reservoir show obvious difference, with ultimate oil recovery factor of 16.21%, 17.57% and 19.74% respectively for Sample 4 (Fig. 5d), and 17.37%, 19.33% and 23.29% for Sample 3 (Fig. 5c). Difference of results obtained by the three method for strong volatile oil reservoir are even pronounced, with ultimate oil recovery factor of 20.82%, 24.16% and 30.45% for Sample 2, and 24.76%, 28.26% and 35.93% for Sample 1 (Fig. 5a). According to the presented results, it is suggested that for typical black oil, with “experiment data-conventional method”, similar results can be obtained with the improved method. For the volatile oil reservoir, it is necessary to correct the experiment data and use the new oil recovery prediction method.
Fig. 5.
Fig. 5.
Oil recovery factor estimated by three methods.
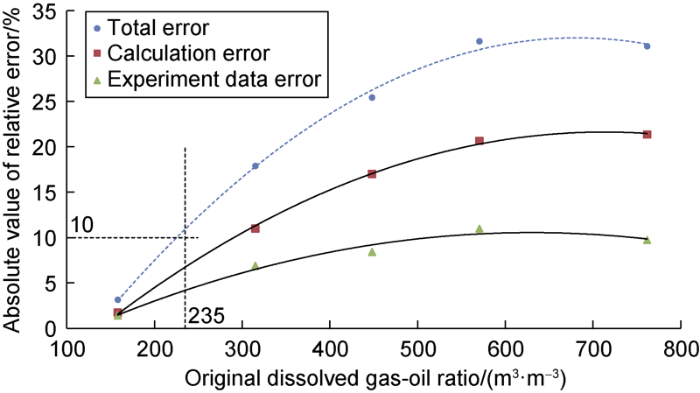
Based on results of ultimate oil recovery factor calculated by “corrected experiment data-improved method”, error resulted from “experiment data-conventional method” and “corrected experiment data-conventional method” is summarized in Fig. 6, with good relation with the original dissolved gas-oil ratio. Within the total error of 10% (in which the error of experiment data accounts for 3.8% and the error by calculation method accounts for 6.2%), if original solution gas-oil ratio is greater than 235 m3/m3, “corrected experiment data-improved method” is recommended. If original solution gas-oil ratio is smaller than 235 m3/m3, “experiment data-conventional method” or “corrected experiment data-conventional method” will not yield great error (within 10%). Due to the complexity of reservoir fluid, including composition, pressure and temperature, whether volatility is strong or not, “corrected experiment data-improved” method is recommended.
Fig. 6.
Fig. 6.
Analysis of error.
Considering multiple degassing experiment and production plan of volatile oil, results calculated by various methods were analyzed. When pressure drops below saturation pressure for either experimenting or reservoir condition, gas started to release from oil, which was a process where liquid gas was transformed into free gas, and liquid oil was transformed into condensate oil. The higher the solution gas-oil ratio and condensate oil in gas phase, the more the original liquid oil transformed into condensate oil (the volume ratio of condensate oil and original liquid oil). For multiple degassing experiment, condensate oil was released along with free gas without being counted as ultimate residual oil. While in reservoir, such amount of oil are produced through two ways: part of it flowing to surface with free gas, and the other was transformed into liquid oil due to pressure drop and flowing to surface. With “Experiment data-conventional method”, condensate oil either in experiment or in reservoir was not taken into account. With “Corrected experiment data-conventional method”, gaseous in experiment was taken into account, but the gaseous in reservoir was ignored. With “Corrected experiment data-improved method”, the influence of condensate oil on oil recovery factor in both experiment and reservoir was taken into account.
According to the results calculated by various methods, the recovery factor in the volatile oil reservoir recovery can reach a comparatively high level by pressure depletion production. Conventional experiences hold the view that, because of the strong contraction of volatile oil, oil recovery level can be quite low. This point of view is concluded by conventional solution-gas drive theory and multiple degassing experiment data. This study, however, indicates that oil contraction is mitigated by experiment data correction and for reservoir production condensate oil provides appreciable contribution.
4. Conclusions
In multiple degassing experiment, the physical properties of crude oil are measured under the condition of complete loss of condensate oil in dissolved gas, which is contradicted with the fact “there is no oil loss from reservoir to surface”. The stronger the oil volatility, the greater the loss of condensate oil. Therefore, due to the multiple degassing experimental principle, the recovery factor in the volatile oil reservoir is underestimated. Conventional method regards the released gas as dry gas. That is, oil production all comes from reservoir liquid oil. While in reality, oil production comes from both oil phase and gas phase. With increasing in oil volatility, the contribution of gaseous oil production also increased. The oil recovery factor is underestimated with the conventional method.
With increasing in oil volatility, the applicability of “experiment data-conventional method” and “corrected experiment data-conventional method” is decreasing, only applicable to typical black oil or weak volatile oil reservoir(with original solution gas-oil ratio lower than 235m3/m3). With “corrected experiment data-improved method”, the influence of gaseous oil in the experimental process and development process has been taken into consideration, and it is not limited by the volatility of crude oil. This study has proved the fact that due to the strong shrinkage of volatile oil, liquid oil is converted into gaseous oil, and produced at surface. The recovery factor in the volatile oil reservoir can also be quite high with pressure depletion production.
Nomenclature
Bg—gas FVF, dimensionless;
Bo—oil FVF, dimensionless;
Bob—oil FVF at saturation pressure from single degassing, dimensionless;
Boi—initial oil FVF, dimensionless;
Bo,j—oil FVF at j-th stage pressure, dimensionless;
Eo—initial oil expansion coefficient, m3/m3;
F—cumulative hydrocarbon production in reservoir, m3;
j—differential liberty pressure stage;
Krg—gas relative permeability, dimensionless;
Kro—oil relative permeability, dimensionless;
qfg—free gas rate, m3/d;
qfo—liquid oil rate, m3/d;
qg—total gas rate, m3/d;
qo—total oil rate, m3/d;
Rgo—instantaneous producing gas-oil ratio by conventional method, m3/m3;
Rgo*—instantaneous producing gas-oil ratio by improved method, m3/m3;
Ro—oil recovery factor by conventional method, %;
Ro*—oil recovery factor by improved method, %;
Rps—cumulative gas-oil ratio by conventional method, m3/m3;
Rps*——cumulative gas-oil ratio by improved method, m3/m3;
Rs—oil solution GOR, m3/m3;
Rsi—initial oil solution GOR, m3/m3;
Rs,j—oil solution GOR at j-th pressure, m3/m3;
Rv—condensate-gas ratio, m3/m3;
Rv,j—condensate-gas ratio at j-th pressure, m3/m3;
So—oil saturation by conventional method, %;
So*—oil saturation by improved method, %;
Swi—initial water saturation, %;
V—original oil in place, m3;
Vfg—remaining free gas volume, m3;
Vfo—remaining liquid oil volume, m3;
Vfoi—initial liquid oil volume, m3;
Vfo,j—initial liquid oil volume at j-th pressure, m3;
Vodb—oil volume in PVT cell in multiple degassing experiment, m3;
Vod,j—oil volume in PVT cell at j-th pressure, m3;
Vp—cumulative oil production, m3;
Vp,j—cumulative condensate oil volume released in multiple degassing experiment, m3;
Vsd,j—total gas volume released at j-th pressure, m3;
Vsd,j-1—total gas volume released at j-1-th pressure, m3;
μg—gas viscosity in reservoir, mPa·s;
μo—oil viscosity in reservoir, mPa·s.
Reference
Methods for determining the type of different oil and gas reservoirs fluid
Fluid and development characteristics of near critical oil and gas reservoirs with high dip angle
Evaluation of development potential of volatile reservoirs in offshore fault block oilfield
The production histories of oil producing gas-drive reservoirs
DOI:10.1063/1.1707566 URL [Cited within: 1]
Establishment of an initial water production evaluation chart for the gas province in the East China Sea
Discussions about experimental analysis standard of volatile oil property
Technologies and practice of CO2 flooding and sequestration in China
Characteristics and exploration direction of volatile oil in Dongpu Depression
A quantitative model for evaluating the impact of volatile oil non- equilibrium phase transition on degassing
DOI:10.1016/S1876-3804(12)60081-0 URL [Cited within: 1]
A new method to correct single flash experiment results of volatile oil
A calculation method of dew-point pressure of gas condensate reservoir
Influences of the new method of PVT data correction on dynamic prediction in volatile oil reservoirs
The material balance as an equation of a straight line
DOI:10.2118/559-PA URL [Cited within: 1]
The material balance as an equation of a straight line: Part II, field cases