Introduction
Carbon dioxide is one of the most common greenhouse gases, countries all over the world are eager to find a way to eliminate its harm to the environment[1,2]. Capturing industrial CO2 and injecting it into deep formation for long-term storage is a promising method to mitigate the greenhouse effect[3]. CO2-EOR technology not only meets this requirement, but also realizes secondary exploitation of the oil field, which can increase oil and gas production to increase economic benefits. The “In Salah” project in Algeria has been successfully injected over 3×104 t of CO2 into fractured sandstone formation in five years, proving the feasibility and considerable economic value of this method[4].
At present, many methods monitoring CO2 storage status have been successfully applied all over the world[5], such as seismic[6,7,8], CT[9] and well temperature logging[10,11], etc. In CO2-EOR technology, CO2 saturation is a key parameter to characterize the distribution and migration of CO2 gas. As an important method of gas saturation evaluation in nuclear geophysical exploration, pulsed neutron logging technology plays an indispensable role in the evaluation of CO2 saturation in the CO2 flooding reservoirs[12,13,14,15,16,17]. In recent years, the Schlumberger company has designed a multifunctional pulsed neutron logging tool, which uses a long source distance YAP (yttrium aluminate) crystal detector combined with a pulsed neutron yield monitor to measure fast neutron scattering cross-section (σf) to quantitatively monitor the gas saturation of the reservoirs[18]. However, characterizing the σf of 14 MeV neutron with inelastic gamma information directly will be affected by the formation lithology to a certain extent, leading to errors in the interpretation of gas saturation.
Aiming at the difference in the deceleration of fast neutrons by CO2, water and heavy oil, based on the theory of fast neutron scattering and secondary gamma distribution and the three-detector pulsed neutron logging technology, this paper proposes a method characterizing σf by the combination of secondary inelastic and capture gamma information to overcome the influence of formation lithology on σf. In view of the presence of shale in the actual reservoirs, the corresponding CO2 saturation interpretation model has been given, and the influences of various factors on the relationship between σf and the formation porosity have been explained. Thus, a more complete quantitative evaluation method for gas saturation of CO2 injection heavy oil reservoirs has been established.
1. Theory and method
The pores of heavy oil reservoirs are generally filled with high-density and high-viscosity heavy oil, and some pores also contain water. In the process of CO2 flooding, the pore fluid is gradually displaced by CO2 gas to form an oil-gas two-phase or oil-gas-water three-phase fluid. CO2 has hydrogen index of zero, and the density, thermal neutron capture cross-section, fast neutron scattering cross-section etc. quite different from formation water and heavy oil. The CO2 injected into the formation will cause great changes in the thermal neutron capture cross-section and fast neutron scattering cross-section of the formation. As a parameter that can provide information independent of the other neutron measurements for formation evaluation[18], the fast neutron scattering cross-section has good performance on monitoring gas saturation of CO2 flooding heavy oil reservoirs quantitatively.
1.1. Fast neutron scattering cross-section of the formation medium
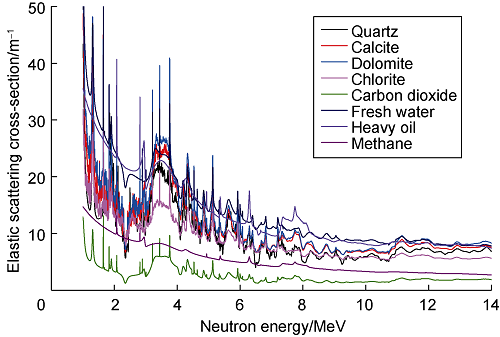
According to the ENDF/B-VII.0 nuclear database[19], the microscopic cross-section of formation elements can be obtained, and then the macroscopic elastic scattering cross-section of the medium can be obtained by the calculation formula. Fig. 1 shows the relationships between the elastic scattering cross-sections of different formation matrix minerals and pore fluids with neutron energy. It can be seen that the elastic scattering cross-section of gas is significantly smaller than that of formation matrix mineral and pore fluids, and this feature of CO2 is particularly obvious. In this paper, the elastic scattering cross-section is taken as σf because of its difference in formation media to evaluate the CO2 saturation quantitatively.
Fig. 1.
Fig. 1.
The relationship between elastic scattering cross- section and neutron energy of different formation media.
The numerical integration method is used to calculate the σf values of formation matrix minerals and pore fluids, and the results are shown in Table 1. It can be seen that the gases, especially CO2, have lower σf, the formation matrix minerals have generally larger σf, and fresh water and heavy oil have even larger and similar σf. Therefore, based on the characteristic of ultra-low elastic scattering cross-section of CO2, the oil-water-gas three- phase fluid in the CO2 flooding heavy oil reservoir can be regarded as gas-liquid two-phase fluid.
Table 1 The σf values of different media with certain densities.
| Medium | Density/ (g∙cm-3) | σf/m-1 | Medium | Density/ (g∙cm-3) | σf/m-1 |
|---|---|---|---|---|---|
| Quartz | 2.65 | 9.64 | Water | 1.00 | 14.00 |
| Calcite | 2.71 | 11.09 | CO2 | 0.50 | 2.53 |
| Dolomite | 2.87 | 11.82 | CH4 | 0.20 | 5.35 |
| Chlorite | 2.76 | 8.64 | Heavy oil | 0.95 | 13.50 |
1.2. Method of characterizing the σf by combining inelastic and capture gamma-ray data
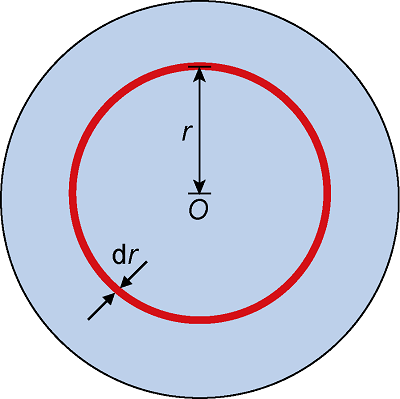
When entering formation, fast neutrons would collide with the formation nuclei and slow down. In this process, secondary inelastic gamma-ray is generated by the inelastic scattering of fast neutrons and formation elements. In the spherical model shown in Fig. 2, the deuterium- tritium neutron source (D-T) located at point O, emitted fast neutrons with an energy of 14 MeV uniformly around, and the spherical surface with a radius of r was used to record the inelastic gamma-ray from the formation.
Fig. 2.
Fig. 2.
Model of infinite and uniform spherical medium.
According to the fast neutron scattering theory[20], the fast neutron flux distribution where inelastic scattering occurs is:
The intensity of inelastic gamma-ray depends on the type of the formation element and its microscopic inelastic scattering cross-section. The number of gamma photons produced by element k in one collision is ik, the corresponding microscopic inelastic scattering cross-section is σk, then the number of gamma rays produced in a spherical shell with a radius of r and a thickness of dr is:
The number of inelastic gamma photons in the sphere model is equal to the integral of dI from r=0 to r=+. With the influence of gamma attenuation considered, assuming that the σf are equal everywhere of the formation, the mass attenuation coefficient (μm) of the formation and the average number of gamma photons (i) generated by the interaction of one fast neutron with the formation elements are constant, ignoring the gamma photon contribution outside the detectors, according to the theory of neutron gamma coupling field[21], the inelastic gamma flux can be expressed as:
Eq. (3) is simplified by Lagrange Mean Value Theorem:
In Eq. (4), α is a proportionality factor related to the source distance, which is a fixed value for a given instrument. It can be seen from Eq. (4) that the inelastic gamma flux is not only related to the value of σf, but also related to the formation density. Therefore, σf can be regarded as a function of inelastic gamma flux and formation density. Based on the multi-detector pulsed neutron logging tool, the formation density can be characterized by the combination of inelastic and capture gamma count ratio of dual-detector[22]:
In Eq. (5), A, B, and C are constants, which are obtained by fitting simulation data or measured data of calibration well.
Combining Eqs. (4) and (5), the quantitative characterization of σf can be realized by the inelastic and capture gamma of the near and far detectors:
where $K=\frac{1}{R\left( \alpha -1 \right)}$ $L=\frac{A\alpha {{\mu }_{\text{m}}}}{\alpha -1}$ $M=\frac{B\alpha {{\mu }_{\text{m}}}}{\alpha -1}$ $N=\frac{C\alpha {{\mu }_{\text{m}}}}{\alpha -1}+\ln \frac{4\pi R}{i{{\sigma }_{\text{in}}}{{\phi }_{\text{0}}}}$
Eq. (6) shows that the σf can be characterized by combining inelastic and capture gamma information of the near and far detectors, and the coefficients K, L, M, and N can be obtained by fitting simulation data or calibrating well measured data.
1.3. Interpretation model of gas saturation in CO2 flooding heavy oil reservoir
σf represents a macroscopic physical characteristic of the reservoir, which follows the physical model of bulk-volume rock. Using Eq. (6) to obtain the value of σf; for sandstone reservoirs filled with CO2 and heavy oil in pores, the σf satisfies the following equation:
Then the gas saturation interpretation model of the reservoir is:
The formation of pure sandstone matrix is an ideal condition, but the actual formation matrix always contains a certain proportion of shale or other solid minerals. Taking the shale-bearing formation as research object, based on the difference in the value of σf of shale and sandstone matrix, σf of the formation satisfies the following equation:
It can be seen from Eq. (9) that the presence of shale will cause changes in the physical model of bulk-volume rock. When the formation contains shale, the shale content at the measurement point and the porosity of the formation need to be combined to correct the sandstone formation model shown in Eq. (7). The interpretation model of gas saturation in shale-bearing reservoir is:
Compared with the gas saturation interpretation model for pure sandstone formation shown in Eq. (8), Eq. (10) takes into account shale-bearing formation conditions. When the formation contains other solid minerals, it is also necessary to modify the gas saturation interpretation model to meet the actual formation matrix conditions.
2. Monte Carlo simulation
Monte Carlo simulation (MCNP) is a random sampling or statistical experiment method. It can be used to simulate neutrons, photons, electrons and their coupled transport processes, which has been widely applied in radioactive logging simulation, response and instrument manufacturing[23]. In this paper, MCNP was used to establish the instrument and formation model to simulate all the processes of fast neutron transport, including fast neutron slowing down to produce inelastic gamma, capture of thermal neutron to produce capture gamma and gamma attenuation. Based on the simulation results, the characterization of σf and gas saturation response were analyzed to realize the quantitative monitoring of gas saturation of CO2 flooding heavy oil reservoir.
2.1. The instrument and formation model
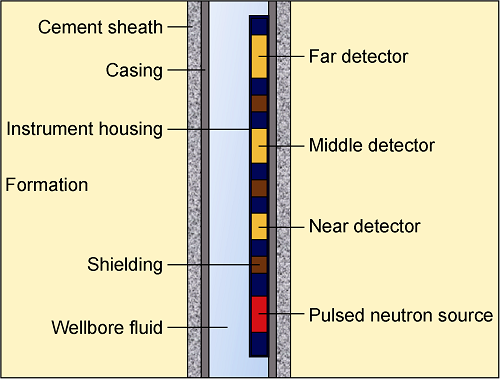
The numerical calculation model built in this study is shown in Fig. 3. The formation model is set up as a casing well with a height of 150 cm and a diameter of 120 cm. The borehole is 20 cm in diameter and filled with fresh water. The formation matrix is sandstone, limestone or dolomite. The casing is 0.7 cm thick stainless steel, and a 3 cm thick CaSiO3 cement filled between the casing and the formation. The reservoir has a porosity changing from 0 to 40% with an interval of 5%, the CO2 saturation changed from 0 to 100%. The formation pressures were set at 35, 50 and 65 MPa, and the formation temperatures were set at 363.15, 393.15 and 423.15 K. The densities of CO2 gas, fresh water and heavy oil were 0.50, 1.00 and 0.95 g/cm3 respectively at the formation pressure of 35 MPa and formation temperature of 363.15 K.
Fig. 3.
Fig. 3.
The model of instrument and formation.
The three-detector pulsed neutron logging tool was used to monitor the CO2 gas saturation with shielding added between the source and each detector. The neutron pulse emission time was designed at 40 μs, and the measurement time of inelastic and capture gamma-ray was 0-40 μs and 50-1000 μs, respectively. The near, middle and far detectors of the logging tool coded 1, 2, and 3, recorded the count of inelastic and capture gamma-ray at the same time. 17-4PH steel was used as the material of the instrument housing, with a thickness of 0.5 cm. The source was a D-T pulsed neutron source, which uniformly emitted high-energy fast neutrons (14 MeV) to the formation. The detector material was LaBr3 crystal, and the source distances of the three detectors were 27.5, 40.0, and 60.0 cm respectively. The crystal of three detectors were 5 cm in diameter and 5, 10 and 10 cm long, respectively.
2.2. Characterization method of fast neutron scattering cross-section
By simulating different reservoirs containing heavy oil and CO2, we obtained the three-detector inelastic and capture gamma counts of different lithologic reservoirs (sandstone, limestone and dolomite) of different porosities (0-30%, interval of 5%) saturated with heavy oil or CO2. The purpose of the combination of inelastic and capture gamma count ratio shown in Eq. (5) is to eliminate the influence of formation density. Considering the counting statistics and accuracy of σf, the gamma information of near and far detectors was selected to quantitatively characterize σf. By Eq. (6) and multiple linear regression method, a equation converting inelastic and capture gamma information to σf has been established:
To verify the applicability of the Eq. (11), the calculated σf values and the theoretical σf values set in the formation model were compared. The error between the calculated and the theoretical values is expressed as:
Table 2 shows the error analysis of the calculated σf and theoretical σf values of the heavy oil saturated and CO2 saturated sandstone reservoirs with different porosities. Table 3 shows the error analysis of the calculated σf and theoretical σf values of the CO2 saturated sandstone, limestone and dolomite reservoirs with different porosities. These calculations were used to verify the accuracy of the characterization equation under different oil-gas- bearing and lithologic conditions. It can be seen that Eq. (11) can characterize the formation σf accurately, and the error between the calculated value and the theoretical value can be controlled within ±2%. Combining inelastic and capture gamma of the pulsed neutron logging can quantitatively characterize the σf of CO2 flooding heavy oil reservoir.
Table 2 Analysis of errors between calculated values and theoretical values of σf of sandstone reservoirs.
| Formation porosity/% | Saturated with heavy oil | Saturated with CO2 | ||||
|---|---|---|---|---|---|---|
| Theoretical σf/m-1 | Calculated σf/m-1 | Error/% | Theoretical σf/m-1 | Calculated σf/m-1 | Error/% | |
| 0 | 9.570 | 9.622 | 0.54 | 9.570 | 9.622 | 0.54 |
| 5 | 9.766 | 9.865 | 1.01 | 9.217 | 9.352 | 1.46 |
| 10 | 9.963 | 10.105 | 1.43 | 8.865 | 8.949 | 0.95 |
| 15 | 10.160 | 10.210 | 0.49 | 8.513 | 8.529 | 0.19 |
| 20 | 10.357 | 10.480 | 1.19 | 8.161 | 8.202 | 0.50 |
| 25 | 10.554 | 10.721 | 1.58 | 7.809 | 7.738 | -0.91 |
| 30 | 10.750 | 10.916 | 1.54 | 7.456 | 7.492 | 0.48 |
Table 3 Analysis of errors between calculated values and theoretical values of σf in three different lithologic reservoirs saturated with CO2.
| Formation porosity/% | Sandstone | Limestone | Dolomite | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Theoretical σf/m-1 | Calculated σf/m-1 | Error/% | Theoretical σf/m-1 | Calculated σf/m-1 | Error/% | Theoretical σf/m-1 | Calculated σf/m-1 | Error/% | |
| 0 | 9.570 | 9.622 | 0.54 | 11.088 | 11.125 | 0.33 | 11.820 | 11.714 | -0.90 |
| 5 | 9.217 | 9.352 | 1.46 | 10.659 | 10.812 | 1.44 | 11.355 | 11.195 | -1.41 |
| 10 | 8.865 | 8.949 | 0.95 | 10.231 | 10.294 | 0.62 | 10.890 | 10.743 | -1.35 |
| 15 | 8.513 | 8.529 | 0.19 | 9.803 | 9.804 | 0.01 | 10.426 | 10.315 | -1.06 |
| 20 | 8.161 | 8.202 | 0.50 | 9.375 | 9.490 | 1.23 | 9.961 | 9.899 | -0.62 |
| 25 | 7.809 | 7.738 | -0.91 | 8.947 | 8.934 | -0.15 | 9.496 | 9.396 | -1.05 |
| 30 | 7.456 | 7.492 | 0.48 | 8.519 | 8.565 | 0.54 | 9.032 | 8.936 | -1.06 |
In actual heavy oil reservoirs, the use of Eq. (11) to characterize the reservoir σf may cause errors because of the influence of factors such as shale content, heavy oil density, formation temperature and pressure, and gas type, etc. The σf obtained by Eq. (11) should be corrected first for the influence of different wellbore-formation factors to ensure the accuracy and realize the universal application of the equation in CO2 flooding effect evaluation.
2.3. Relationship between fast neutron scattering cross-section and CO2 saturation
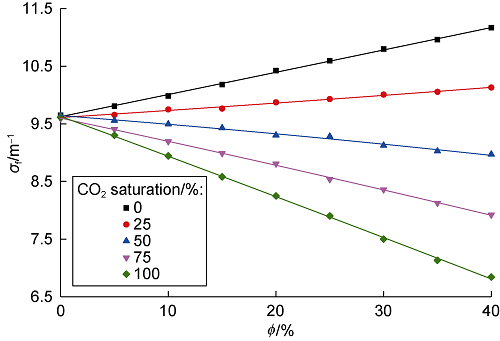
The instrument and formation model shown in Fig. 3 was established based on Monte Carlo numerical calculation method. Under the condition of a sandstone reservoir with the mixed fluid of heavy oil and CO2 in pores, the formation porosity is set to 0-40% with an interval of 5%, and the CO2 saturation is set to 0, 25%, 50%, 75% and 100% respectively. By the characterization equation of σf, the relationship between σf and formation porosity under different CO2 saturations is obtained, as shown in Fig. 4. It can be seen that the CO2 saturation of the reservoir has a great influence on the relationship between σf and porosity. At low CO2 saturation, heavy oil is the main component of pore fluid, except for the formation matrix, the heavy oil dominates the deceleration to neutrons. As the CO2 saturation increases, CO2 in the pores gradually increases, the deceleration of CO2 on neutrons becomes gradually significant and finally dominant. Compared with the formation matrix, heavy oil has higher σf, while CO2 has much lower σf. Therefore, at low CO2 saturations (0 and 25%), σf shows an upward trend with the increase of formation porosity; at high CO2 saturations (50%, 75% and 100%), σf shows a clear downward trend with the increase of formation porosity. It can be seen that the macroscopic σf is determined by porosity and gas saturation in CO2 flooding heavy oil reservoir. The macroscopic σf of formation can be characterized with gamma count, then combined with the physical model of bulk-volume rock, the gas saturation of the CO2 flooding heavy oil reservoir can be quantitatively monitored.
Fig. 4.
Fig. 4.
Relationship between σf and formation porosity.
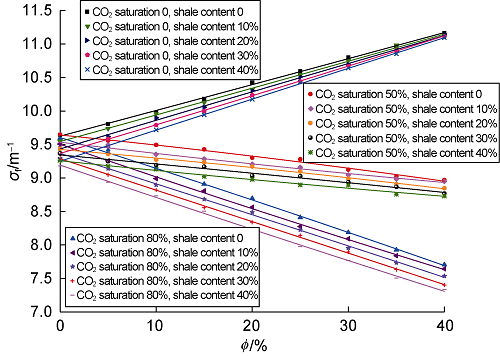
Actual reservoirs often contain different types of shale which affect the deceleration ability of the reservoir to fast neutrons. The CO2 saturation of shale- bearing reservoir should be calculated by Eq. (10). Taking chlorite as the shale component for research, based on the instrument and formation model shown in Fig. 3, the sandstone formation was set at shale contents of 10%, 20%, 30%, and 40%, porosities of 0-40% with an interval of 5%, and CO2 saturations of 0, 50%, and 80%, respectively. The relationships between σf and the porosity of the formation at different shale contents were simulated, and the results are shown in Fig. 5. In general, when the shale is chlorite, the presence of shale makes the calculated values of σf significantly smaller than those of the pure sandstone formation. At high CO2 saturation, the curves of σf with formation porosity at different shale contents are approximately parallel. At low CO2 saturation, with the increase of porosity, the influence of shale content on σf gradually decreases. This means that the change of σf caused by shale is dependent upon the formation porosity and shale content, and in actual reservoirs, it is more reasonable to interpret CO2 saturation of shale-bearing formations by using σf and the physical model of bulk-volume rock jointly.
Fig. 5.
Fig. 5.
Influence of shale content on the relationship between σf and formation porosity.
3. Analysis of influencing factors
This paper proposes a quantitative interpretation method for evaluating the gas saturation of CO2-injected heavy oil reservoirs by using σf. However, in actual CO2-injected heavy oil reservoirs, the gas saturation evaluation method may fail sometimes due to the uncertainty of logging environment. Therefore, it is necessary to analyze and correct the formation influencing factors (such as temperature, pressure and wellbore environment, etc.), which is the basis for ensuring the applicability of monitoring CO2 gas saturation with σf quantitatively.
3.1. Influence of reservoir temperature and pressure
Changes in formation temperature and pressure are the main factors that cause the dissolution of CO2 in heavy oil to form miscible oil for CO2-injected reservoirs. Due to differences in CO2 solubility, the miscible oil varies in density under different temperature and pressure conditions. According to the research of Marra et al.[24], the change in the density of the miscible oil caused by the changes of temperature and pressure can be calculated according to the following equations:
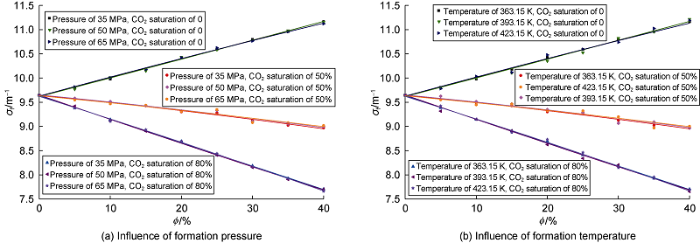
Based on the instrument and formation model shown in Fig. 3, under the condition of a sandstone formation, the formation porosity is set to 0-40% with an interval of 5%, and the CO2 gas saturation is set at 0, 50% and 80%. The formation temperature is set to 363.15 K, and the formation pressure is changed to 35, 50, 65 MPa to study the influence of formation pressure. Similarly, the formation pressure is set to 35 MPa, and the formation temperature is changed to 363.15, 393.15 and 423.15 K to study the influence of formation temperature. It can be seen from Fig. 6 that the formation temperature and pressure conditions have little effect on the CO2 gas saturation calculated with σf. According to calculation by Eqs. (13) and (14), when the formation temperature is 363.15 K and the formation pressure of heavy oil reservoir increased from 35 MPa to 65 MPa, the density of the miscible oil would increase from 0.950 to 0.963 g/cm3. Similarly, at the formation pressure of 35 MPa, when the formation temperature increased from 363.15 K to 423.15 K, the density of the miscible oil would increase from 0.950 g/cm3 to 0.983 g/cm3. Clearly, the variation range of miscible oil density caused by the change of formation temperature and pressure is relatively small, so the deceleration capacity of formation to fast neutrons hardly changes. Together with the formation matrix factor, the deceleration capacity of the reservoir to fast neutrons remains unchanged. Within the studied formation temperature and pressure ranges, the miscible oil density will not change drastically, and the change in heavy oil density caused by changes in reservoir temperature and pressure is not enough to affect the deceleration ability of the formation to fast neutron. Therefore, when evaluating CO2 gas saturation in CO2 flooding heavy oil reservoir with σf, the influences of formation temperature and pressure can be ignored.
Fig. 6.
Fig. 6.
The influences of formation temperature and pressure on the relationship between σf and formation porosity.
3.2. The influence of heavy oil density
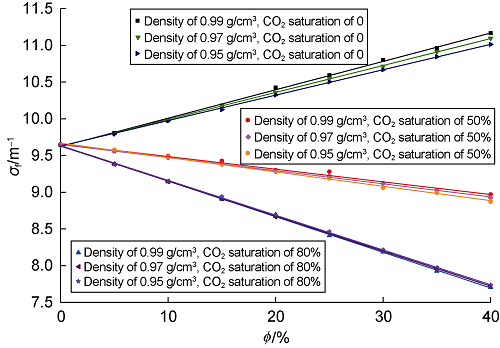
In heavy oil reservoirs developed by CO2 flooding, heavy oil would change in density with certain temperature and pressure range due to the changes of CO2 solubility with temperature and pressure[25]. At the temperature of 333.15 K, when the pressure increases from 35 MPa to 65 MPa, calculation shows the density of heavy oil is 0.94 to 1.00 g/cm3. Based on the instrument and formation model shown in Fig. 3, the relationships between σf and porosity at the heavy oil densities of 0.95, 0.97, and 0.99 g/cm3 were simulated. It can be seen from Fig. 7 that at the low CO2 saturation (0), the density of heavy oil has some influence on σf; with the increase of heavy oil density, the calculated σf shows an increasing trend. But in the reservoir with high CO2 saturation (80%), the influence of heavy oil density is not obvious, the reason is that most of the reservoir fluid has been displaced by CO2. For actual heavy oil reservoirs developed by CO2 flooding, the heavy oil density after multiple cycles of CO2 injection would change in much smaller range than that studied in this work. The changes in heavy oil density after CO2 flooding has a negligible effect on the measurement of CO2 saturation.
Fig. 7.
Fig. 7.
The influence of heavy oil density on the relationship between σf and formation porosity.
3.3. Influence of borehole fluid type
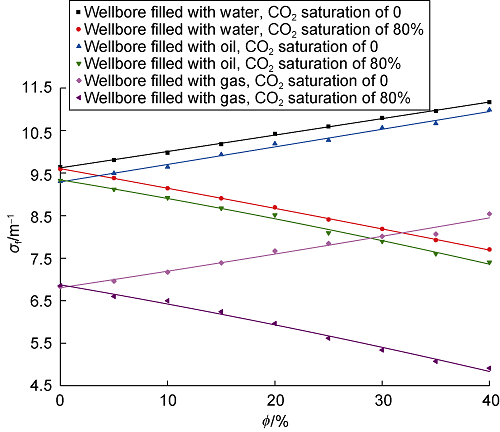
CO2 flooding in heavy oil reservoir often takes multiple cycle injection or alternate water and CO2 injection. Therefore, the fluid in wellbore would change from drilling fluid to heavy oil, CO2 or water. To study the influence of wellbore fluid on the evaluation of CO2 saturation with σf in CO2 flooding reservoir, based on the instrument and formation model shown in Fig. 3, with wellbore fluid set as water, gas, and heavy oil respectively, the relationships between σf and formation porosity under the different wellbore fluids were simulated, and the results are shown in Fig. 8. It can be seen that the curves of σf with formation porosity under different wellbore fluid conditions are parallel. The difference in the deceleration ability of water and oil to fast neutrons is small. The value of σf when the wellbore is filled with oil is slightly smaller than that when wellbore is filled with water. Compared with water and oil, gas has much weaker deceleration capacity to fast neutrons, so the value of σf when the wellbore is filled with gas significantly decreases. Therefore, when evaluating effect of CO2 flooding in heavy oil reservoir with σf, the gas-bearing property needs to be corrected according to the fluid type in the wellbore.
Fig. 8.
Fig. 8.
Influence of wellbore fluid on the relationship between σf and formation porosity.
3.4. Influence of methane content of the reservoir
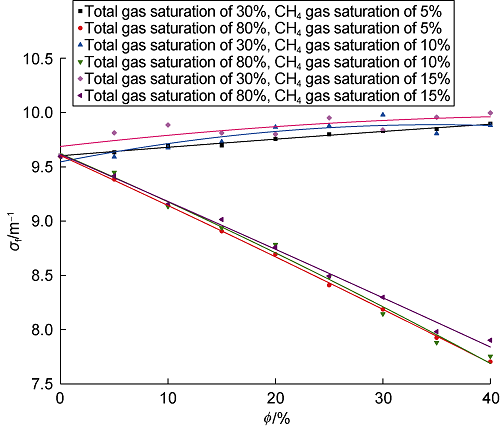
In multiple cycles of CO2 injection in heavy oil reservoir, if the reservoir contains CH4, the injected CO2 would mix with a certain proportion of CH4, and CH4 would accumulate during the CO2 flooding, affecting the evaluation of CO2 saturation. Based on the instrument and formation model shown in Fig. 3, with the total gas saturations (CO2 and CH4) of the formation set at 30% and 80%, and the CH4 saturations set at 5%, 10% and 15% respectively, the relationships between σf and formation porosity under different mixing ratios of the two kinds of gases were simulated, and the results are shown in Fig. 9. It can be seen when the total gas saturation is high, the influence of CH4 content is smaller. When the total gas saturation is low, the influence of CH4 content although increases, is still not obvious. Therefore, it is difficult to distinguish CH4 and CO2 using evaluating CO2 saturation. Compared with the formation matrix, heavy oil and water, CH4 and CO2 both have lower σf values. Although the σf of CH4 is slightly larger than that of CO2, the two kinds of gases take a relatively small proportion of the total volume of the formation, and small amount of CH4 in the pores does not affect the deceleration ability of the formation to fast neutrons. In fact, the calculation result of CO2 saturation is closer to the total saturation of CO2 and CH4. Therefore, it is difficult to eliminate the calculation error in CO2 saturation caused by the presence of CH4 when evaluating the gas saturation of reservoir with σf. To ensure the accuracy of CO2 saturation monitoring during the CO2-EOR project, the CH4 content after multiple cycles of CO2 injection must be strictly controlled.
Fig. 9.
Fig. 9.
Influence of CH4 content on the relationship between σf and formation porosity.
4. Case study
An example was simulated to verify the effectiveness of the method presented in this paper. The formation is 234 m thick in total and separated by clay layers. The pore fluids of the formation are different combinations of heavy oil, fresh water and CO2. Table 4 shows the lithology, porosity, density, shale content, fluid properties and saturation parameters of each reservoir. During the simulation logging process, the tool slided along the wellbore wall from bottom to top to detect and record the inelastic and capture gamma information of the multi-detectors. The information was converted into σf, and combined with gas saturation calculation method and correction method, CO2 saturations of the reservoirs were obtained.
Table 4 Basic parameters of each reservoir in the example.
| Reservoir | Matrix | Porosity/% | Density/(g·cm-3) | Shale content/% | Pore fluid composition |
|---|---|---|---|---|---|
| A | Sandstone | 30 | 2.114 0 | 14 | With CO2 saturation of 20%, water saturation of 30%, and oil saturation of 50% |
| B | Sandstone | 20 | 2.484 0 | 0 | With CO2 saturation of 70%, water saturation of 10%, and oil saturation of 20% respectively |
| C | Sandstone | 35 | 1.941 5 | 15 | With CO2, water, oil and CH4 saturations of 50%, 5%, 25%, and 20% respectively |
| D | Limestone | 25 | 2.182 5 | 0 | With CO2 and oil saturations of 50% and 50% |
| E | Mudstone | 30 | 2.046 6 | 71 | With CO2 and oil saturations of 70% and 30% respectively |
| F | Sandstone | 20 | 2.250 0 | 31 | With CO2 and water saturations of 60% and 40% respectively |
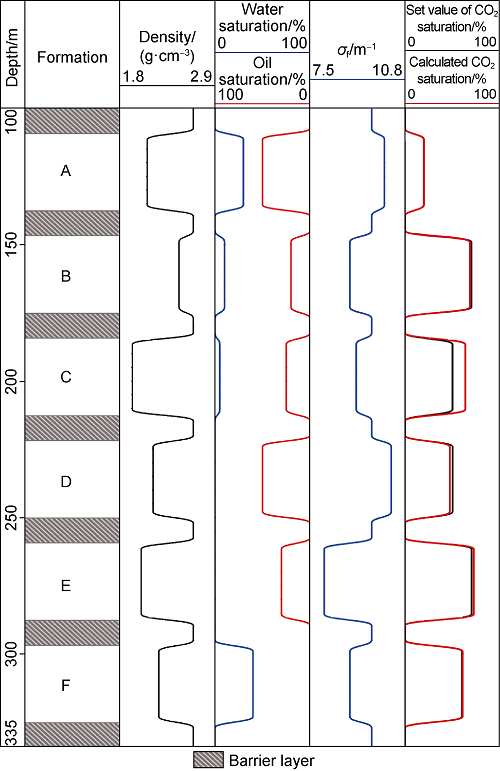
From the interpretation results shown in Fig. 10, it can be seen that the calculation errors of CO2 saturations of layer A to layer F are 0.3%, 1.7%, 13.5%, 2.9%, 2.4%, and 0.6%, respectively. The formation lithology and shale content do not affect the error of the method in evaluating CO2 saturation. No matter whether the formation contains shale, the calculation errors of CO2 saturation can be controlled within 3%. Therefore, monitoring CO2 saturation of heavy oil sandstone reservoir with σf is an effective method. When the formation contains CH4 (layer C), the calculation error of CO2 saturation is larger (13.5% for layer C). This phenomenon also confirms this method has the shortcoming of unable to distinguish CO2 and CH4.
Fig. 10.
Fig. 10.
Interpretation results of the simulation example.
5. Conclusions
CO2 differs widely from oil and water in fast neutron deceleration ability. In this work, the fast neutron scattering cross-section was applied to the quantitative monitoring of gas saturation of CO2 flooding heavy oil reservoir, the gas saturation evaluation model was established to realize quantitative calculation of CO2 saturation. This method provides technical support for gas saturation monitoring in heavy oil reservoir developed by CO2 flooding.
Based on the three-detector pulsed neutron logging technology, the inelastic and capture gamma of the near and far detectors can be combined to realize the characterization of fast neutron scattering cross-section of the reservoir. The shale-bearing reservoir is different from pure lithology reservoir in fast neutron scattering cross- section. Hence, it is more reasonable to evaluate the CO2 saturation by using shale content and physical model of bulk-volume rock of the reservoir. The changes of miscible oil density caused by the variations of formation temperature and pressure are relatively small and don’t affect the deceleration ability of the heavy oil and CO2 miscible fluid to fast neutrons, so the influence of the formation temperature, pressure and heavy oil density to CO2 saturation evaluation can be ignored. Compared with the formation matrix, CH4 and CO2 are both low in values of fast neutron scattering cross-section, the presence of CH4 would cause errors in the evaluation of CO2 saturation. The CH4 content must be controlled strictly when monitoring CO2 saturation. In addition, the type of wellbore fluid greatly affects the measurement of fast neutron scattering cross-section. When using the fast neutron scattering cross-section to judge the effect of CO2-injected heavy oil reservoir, the gas-bearing property must be corrected according to the type of fluid in the wellbore.
The simulation results of an example show that calculated CO2 saturations by this method have errors of less than 3% when there is no CH4 in the reservoir, verifying the effectiveness of the method.
Nomenclature
A, B, C—constants, g/cm3;
i—the average number of gamma photons produced by inelastic scattering of a fast neutron colliding with a formation element;
ik—the number of gamma photons produced by element k in a collision;
p—formation pressure, MPa;
I—the number of gamma rays;
r—the radius of the sphere centered on the neutron source, m;
dr—the thickness of the spherical shell with radius r, m;
R—source distance of detector, m;
Sg—CO2 saturation, %;
T—formation temperature, K;
Vsh—shale content, %;
α—scale factor related to source distance;
ε—the error between the calculated value and the theoretical value of σf, %;
λs—fast neutron scattering free path, m;
μm—mass attenuation coefficient, m2/kg;
ρ—formation density, kg/m3;
Δρp, Δρt—the change in the density of the miscible oil caused by changes of formation pressure and temperature, g/cm3;
ρ0—density of miscible oil under formation pressure of 0.1 MPa and formation temperature of 288.7 K, g/cm3;
σf—fast neutron scattering cross-section, m-1;
σf,cal—calculated value of σf, m-1;
σf,gas, σf,mat, σf,oil, σf,sh—fast neutron scattering cross-section of CO2, formation matrix, oil, and shale, m-1;
σf,real—the theoretical value of σf set in the formation model, m-1;
σk—the micro-inelastic scattering cross-section of element k in a collision, m-1;
σin—the inelastic scattering cross-section of the formation, m-1;
ϕ—formation porosity, %;
ϕ0—neutron source intensity;
ϕf(r)—fast neutron flux, m-2;
ϕin(R)—inelastic gamma flux, m-2;
ϕcap1, ϕcap3—the gamma counts captured by near and far detectors;
ϕin1, ϕin3—the inelastic gamma counts of near and far detectors.
Reference
Greenhouse gas reporting for geologic sequestration of carbon dioxide
Greenhouse gas emissions along the Norwegian gas value chain
Technologies and practice of CO2 flooding and sequestration in China
In Salah CO2 storage JIP: CO2 sequestration monitoring and verification technologies applied at Krechba, Algeria
DOI:10.1016/j.egypro.2011.02.289 URL [Cited within: 1]
Experimental analyses of mass transfer and heat transfer of post-combustion CO2 absorption using hybrid solvent MEA-MeOH in an absorber
DOI:10.1016/j.cej.2014.08.064 URL [Cited within: 1]
DoReMi: A passive, geophysical monitoring technique for CO2 injection
Monitoring CO2 response on surface seismic data; a rock physics and seismic modeling feasibility study at the CO2 sequestration site, Ketzin, Germany
DOI:10.1016/j.jappgeo.2010.05.004 URL [Cited within: 1]
4D seismic or CO2 in formation-fast neutron cross section: SPWLA 25th Formation Evaluation Symposium of Japan
CO2 injection in carbonates
Temperature logging in injection wells
Thermal signature of free-phase CO2 in porous rocks: Detectability of CO2 by temperature logging
Expanding application of multi-detector pulsed neutron instrumentation for quantitative gas saturation monitoring in gas-filled boreholes: SPWLA 58th Annual Logging Symposium
Monte Carlo simulation for determining gas saturation using three-detector pulsed neutron logging technology in tight gas reservoir and its application
DOI:10.1016/j.apradiso.2013.03.092 URL [Cited within: 1]
CO2 sequestration monitoring in a low salinity reservoir
Time-lapse carbon dioxide monitoring with pulsed neutron logging
DOI:10.1016/S1750-5836(07)00071-0 URL [Cited within: 1]
Pulsed neutron monitoring of the first CO2 EOR pilot in the Middle East
Monitoring CO2 saturation using three-detector PNC logging technique for CO2-EOR in heavy oil reservoir: SPWLA 60th Annual Logging Symposium
Fast neutron cross-section measurement physics and applications: SPWLA 57th Annual Logging Symposium
ENDF/B-VII. 0: Next generation evaluated nuclear data library for nuclear science and technology
DOI:10.1016/j.nds.2006.11.001 URL [Cited within: 1]
Theory of neutron logging I
DOI:10.1190/1.1438839 URL [Cited within: 1]
A method to describe inelastic gamma field distribution in neutron gamma density logging
DOI:10.1016/j.apradiso.2017.08.024 URL [Cited within: 1]
Dual-spacing hydrogen index correction method for neutron gamma density measuring in LWD
MCNP: A general Monte Carlo n-particle transport code, version 5
Density of crude oil saturated with CO2
DOI:10.2118/16350-PA URL [Cited within: 1]
CO2 assisted steam flooding in late steam flooding in heavy oil reservoirs