Introduction
Emulsion is the main product of interaction between oil phase and low interfacial tension flooding systems such as surfactant flooding, alkali water flooding and alkali-surfactant-polymer ternary compound flooding in porous media[1,2,3,4]. Lu et al.[5] carried out oil displacement experiment in transparent sand filling pipe, intuitively proved the essence of oil displacement in ultra-low interfacial tension chemical system, that is, the emulsion formed by the interaction of chemical reagent and crude oil displaces the residual oil to form oil wall, and the emulsion is then displaced by subsequent fluid. It is of great significance to study the emulsion flow, occurrence characteristics and conformance control mechanisms in porous media for improving the performance of chemical flooding system represented by surfactant flooding.
Becher et al.[6] first proposed the concept of emulsion displacement in porous media, many scholars then use the traditional laboratory core experiment method to study the flow pressure drop of emulsion, the parameter changes of produced fluid such as viscosity, composition and water cut, and the effect of emulsion displacement on EOR[7,8,9,10]. Kumar et al.[11] analyzed the pressure response and application effect of oil-in-water (O/W) and water-in-oil (W/O) emulsion in the process of core flow, and considered that low viscosity O/W emulsion could inhibit viscous fingering and avoid excessive injection pressure. However, these studies based on macroscopic scale are difficult to investigate the flow and occurrence characteristics of emulsion. In recent years, a large number of microscopic visualization experiments have been carried out to visually present the formation process and flow dynamics of emulsion[12,13,14,15,16,17]. Yu et al.[18], using the microfluidic model, systematically introduced the formation process and mechanism of O/W emulsion and W/O/W complex emulsion formed by strong and weak emulsification systems and crude oil in porous media. Most of the microfluidic models are 2D models with uniform depth, and the pore throat structure is simple. This kind of models weakens the pore-throat jamming effect, which has important influence on the formation of emulsion, thus it is difficult to present the emulsion bands observed by Lu et al.[5]. Xu et al.[19] designed a 2.5 D microfluidic model with continuous depth changes, which strengthens the pore-throat jamming effect and intuitively shows the phenomenon that the emulsion plug high permeability area to make the subsequent injection fluid flow to low permeability area. However, compared with real cores, these studies still have the defects of regular pore throat structure in microfluidic models and smooth surface of manufactured materials[20,21,22,23,24]. Micro computed tomography (Micro-CT) is a high-precision monitoring method which can visually present the occurrence state of multiphase fluid at pore scale. It has been applied to the study of multiphase fluid flow mechanism by domestic and foreign scholars, and has achieved many in-depth research achievements at micro scale in terms of microscopic residual oil occurrence and carbon dioxide burial state[25,26,27]. The establishment of emulsion identification and monitoring methods suitable for Micro-CT scanning, and apply to the study of EOR technology can help to deeply understand the microscopic occurrence characteristics and conformance control mechanisms. In this study, synchronous scanning of core displacement experiment based on Micro-CT is employed to visually present the emulsion occurrence state in artificial sandstone core, and a series of quantitative image processing methods are chosen to systematically evaluate and investigate its occurrence characteristics and conformance control mechanisms at the pore-scale.
1. Synchronous scanning of core displacement experiment based on Micro-CT
1.1. Experimental materials and design
The mineral oil with a kinematic viscosity of 34.5 mm2/s and a density of 0.84 g/cm3 at 25 °C is used in experiments. Pure concentration of surfactant sodium dodecyl sulfate (SDS), cosolvent n-butanol and NaCl for analysis are purchased from Shanghai Aladdin Biochemical Technology Co., Ltd. The specific experiment design is as follows: firstly, add 4% SDS, 4% n-butanol and 2% NaCl to deionized water and stir until the solute is completely dissolved. Then mix aqueous phase with mineral oil at the volume ratio of 1∶1, and carry out the emulsification at 25 °C for 30 min at 6000 r/min with a constant temperature agitator. The prepared emulsion is miscible with water and belongs to O/W. The simulated formation water is replaced with 2% NaCl. Developer CH2I2 with a concentration of 5% is added to the oil phase to enhance the gray difference between oil and water phases, which is more conducive to image segmentation[20].
The cores used in experiments are artificial sandstone cores, and the physical parameters are shown in Table 1. In the E-O group, developer is added into the oil phase of emulsion to identify the emulsion and oil phase, and then the emulsion is distinguished by data analysis. No developer is added in the emulsion of E-W group, and only the remaining oil is identified. In this study, the emulsion formed by the interaction between chemical reagents and oil phase is prepared in advance and then being injected into the core, so as to distinguish the emulsion from oil phase, verify the effectiveness of the emulsion and analyze its effect of EOR.
Table 1 Core parameters and experimental scheme.
| Group | Gas Porosity/% | Gas Permeability/10-3 μm2 | Diameter/mm | Length/mm | Scheme | Development phase |
|---|---|---|---|---|---|---|
| E-W | 27.3 | 230.2 | 7.85 | 50.02 | No developer in emulsion | Oil (Not in emulsion) |
| E-O | 28.1 | 295.7 | 7.96 | 50.08 | Developer in emulsion | Oil (Include oil in emulsion) |
1.2. The procedures
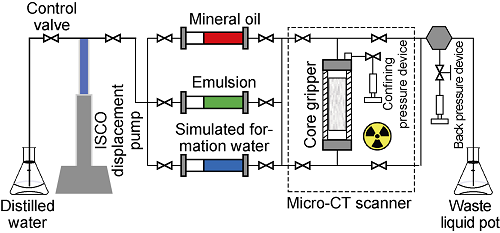
Micro-CT scanning instrument is nano Voxel-3502E of Tianjin Sanying Precision Instrument Co., Ltd., with a resolution of 2.1 μm. Vertically place the core on the sample table, and the flow from core bottom to top is defined as positive direction. The experimental device is shown in Fig. 1. The fluid is injected into the core at a constant rate of 0.02 mL/min. The specific experiment process is as follows: (1) Clean and dry the core, put it into a carbon fiber core gripper[25], add confining pressure to 12 MPa, add back pressure to pore pressure of 8 MPa, and perform CT scan on the dry core; (2) Connect the outlet end of the core holder with the vacuum pump, and vacuum the core for 30 min. Positively inject simulated formation water with 100 times core pore volume (PV), and then place the core for 12h until the ion exchange equilibrium between water phase and pore wall is reached. Inject mineral oil 50 PV in reverse direction, and then scan the core saturated with oil by CT; (3) Carry out forward water flooding over 10 PV until there is no oil phase at the liquid outlet end, and scan the core by CT; (4) Carry out forward emulsion displacement for 2 PV and then scan the core by CT; (5) Carry out forward water flooding for 10 PV and then scan the core by CT. During the whole experiment, keep the position of core holder in CT scanner unchanged, that is, in-situ scanning.
Fig. 1.
Fig. 1.
Schematic diagram of experimental device.
1.3. Image processing
Three-phase segmentation of oil, water phase and rock matrix and the oil-water phase extraction refer to the research of Li et al.[25, 28]. In order to reduce the calculation difficulty and ensure that the data can effectively characterize the core, a series of 3D data (50× 50×50 voxels to 1300×1300×1300 voxels) are segmented, and the porosity and development phase saturation of different scanning data are calculated (Fig. 2). When the voxel is greater than 1×108, the curves of each parameter gradually tend to be flat, that is, the lower limit of the experimental characterization unit volume is 1×108. In this paper, a region with the size of 1200×1200×1000 voxels is selected for study.
Fig. 2.
Fig. 2.
The variation of development phase saturation and porosity with the volume of data.
2. Emulsion occurrence characteristics in porous media
In this study, the occurrence state of the development phase in E-O group is reconstructed (Fig. 3). In the process of saturating oil, the oil phase in each pore is interconnected, occupying most pores in the form of continuous phase (Fig. 3a, 3e). After water flooding, the remaining oil mainly exists in two forms: one is irregularly distributed at pore edge in the swept area of water flooding, the other is contained in the unaffected area and occupies the whole pore (Fig. 3b, 3f). After emulsion flooding, the emulsion enters pore and occupies pore center in spherical form (Fig. 3c, 3g). The subsequent water flooding dilutes the surfactant in emulsion, resulting in a deterioration of the emulsion sphericity (Fig. 3d, 3h). It can be concluded that the emulsion exists in the pores in the form of discontinuous phase and nearly spherical shape.
Fig. 3.
Fig. 3.
Two-dimensional and three-dimensional morphological changes of E-O group.
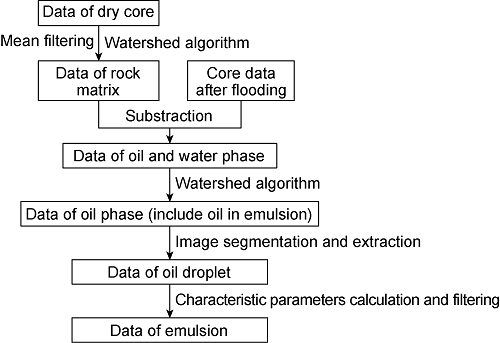
Define sphericity as emulsion morphological characteristic parameter, as shown in Eq. 1. The closer the sphericity value is to 1, the more spherical the droplet is. Identify the development phase in the core and calculate its sphericity data, then screen the development phase with a sphericity of 0.9-1.1, that is, emulsion. Thus, the emulsion identification method and technical flow are established (Fig. 4). According to the technical flow, the emulsion trapped in the core after emulsion flooding is identified, and the results are shown in Fig. 5.
Fig. 4.
Fig. 4.
Flow chart of emulsion identification and extraction.
Fig. 5.
Fig. 5.
The three-dimensional reconstruction of emulsion in E-O group after emulsion flooding (different colors represent discontinuous emulsion).
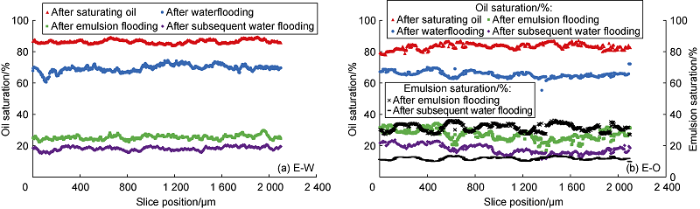
The oil saturation of E-W and E-O groups is calculated, and the emulsion saturation of E-O group is obtained according to its extraction results (Fig. 6). In the stage of saturating oil and water flooding, the trend and average value of the two groups are basically the same, indicating that the parallel experimental design is reasonable. The average oil saturation of E-O group after separating emulsion is similar to that of E-W group, which proves that the sphericity parameter can effectively distinguish residual oil phase and emulsion. In the process of emulsion seepage, the Jiaming effect caused by emulsion droplet changes water phase flow direction, and the residual oil after water flooding is greatly mobilized. The average oil saturation decreases from 69.5% to 25.4%. In the subsequent water flooding process, most of the emulsion outflow from the core outlet, and the average emulsion saturation trapped in the pores decreases from 31.5% to 11.9%.
Fig. 6.
Fig. 6.
Oil and emulsion saturation distribution in different experimental stages (sampling along the displacement direction, slice position 0 indicates sampling position near the displacement entrance end).
2.1. Emulsion occurrence state in pores
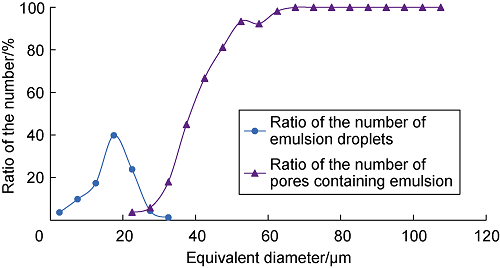
All pores and emulsions are segmented and extracted to obtain their volumes, and the equivalent diameters are calculated according to the spherical volume calculation formula. Taking equivalent diameter 5 μm as step length, the pore is divided into 22 statistical intervals (the equivalent diameter of pore is 0-110 μm), and the emulsion is divided into 8 statistical intervals (the equivalent diameter of emulsion is 0-35 μm). The ratio of emulsion droplet in each emulsion statistical interval to total emulsion droplet after subsequent water flooding is calculated, and the ratio of pore trapping emulsion in each pore statistical interval to total pore is also obtained (Fig. 7). It can be seen that due to the uneven pore distribution, the emulsion shear effect in seepage process is not uniform, resulting in different sizes of emulsion. In the subsequent water flooding stage, the emulsion which is effectively trapped in the pores and produce microscopic flooding effect has similar particle size, and the average equivalent diameter is 15-25 μm. The proportion of pore trapping emulsion starts to increase significantly when the pore equivalent diameter is 30-35 μm, and it reaches more than 90% when the equivalent diameter is 50-55 μm. Therefore, the pore equivalent diameter that can play an effective trapping effect is 30-55 μm. This conclusion provides an experimental basis for the idea of matching emulsion particle size and pore throat in deep conformance control. By controlling particle size, the emulsion can be matched with pore structure, and a part of emulsion can be effectively trapped in the waterflooded area to play the role of plugging, so that the subsequent injection fluid enters the unswept region and then mobilizes the remaining oil.
Fig. 7.
Fig. 7.
Ratio of the number of emulsion droplets and the number of pores trapping emulsion.
The pore occupancy (Eq. 2) is defined as the characterization parameter to quantitatively describe the emulsion occurrence state in the pores. During data processing, the value of water and oil phase is 0, and the value of emulsion is 1:
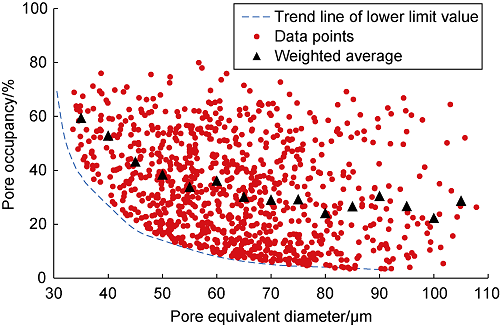
By calculating the emulsion volume ratio in pores, the relationship between emulsion particle size and pore size can be clarified, which provides a reference for emulsion flooding. With the increase of pore equivalent diameter, the pore occupancy of emulsion gradually decreases (Fig. 8). The trapped emulsion in pores has the lower limit of pore occupancy (the blue dotted line in Fig. 8), indicating that the emulsion whose volume is smaller than the product of pore occupancy lower limit and the pore volume will not be effectively trapped in the pore to play a part in conformance control.
Fig. 8.
Fig. 8.
Relationship between emulsion pore occupancy and pore equivalent diameter.
According to the lower limit of pore occupancy, the lower limit design formula of emulsion-pore plugging is obtained (Eq. 3).
The product of pore volume and emulsion occupancy is equal to emulsion volume, thus the lower limit of emulsion particle size is:
The emulsion particle size can be designed according to the above formula, so as to match with the pore throat in the process of conformance control.
2.2. Seepage emulsion flooding
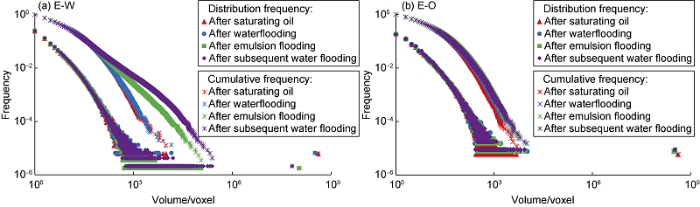
After each displacement stage, the morphology of the trapped fluid in pores is closely related to the flow in displacement process. Blunt et al.[29,30,31] through statistical research shows that the oil phase size distribution in the pore follows the power law relationship, indicating that the seepage process conforms to the classical percolation theory[25,26], which provides a theoretical basis for subsequent numerical simulation based on percolation theory. The development phases volume distribution frequency of the two groups is shown in Fig. 9. To reduce the disturbance error of low-frequency points, high-frequency data points are selected to fit the power-law relation of volume frequency distribution, and the results are shown in Table 2. For E-W group, compared with water flooding, the volume and number of large oil clusters decrease rapidly after emulsion flooding, and the small oil clusters increased sharply. Subsequent water flooding not only mobilizes the residual oil which is not swept by emulsion, but also the emulsion trapped in pores. The emulsion mobilized at this stage may continue to be cut into smaller oil clusters in the flow process, and may also aggregate with other oil clusters. In Fig. 9, both the number of small oil clusters and the volume of some small oil clusters increases. According to the fitting results in Table 2, the volume distribution of oil clusters in each stage is still consistent with the classical percolation theory. The fitting results of the two groups show an increase in the power index, which means that the mobilization of residual oil is more difficult. The classical percolation theory model can not only predict the seepage of oil and water phase at pore-scale, but also predict the volume distribution of oil phase and emulsion in the process of emulsion seepage by selecting different indexes.
Fig. 9.
Fig. 9.
Volume distribution frequency of development phase.
Table 2 Parameters of power law fitting formula of development phase volume distribution frequency.
| Experimental stage | E-W group | E-O group | ||||
|---|---|---|---|---|---|---|
| Coefficient | Power exponent | R2 | Coefficient | Power exponent | R2 | |
| After saturating oil | 1.404 5 | -1.733 | 0.958 6 | 1.144 8 | -1.726 | 0.970 9 |
| After waterflooding | 1.149 3 | -1.676 | 0.968 5 | 1.241 3 | -1.751 | 0.971 1 |
| After emulsion displacement | 1.098 9 | -1.657 | 0.968 7 | 0.997 2 | -1.701 | 0.984 2 |
| After subsequent water flooding | 1.094 9 | -1.660 | 0.967 3 | 1.118 8 | -1.694 | 0.983 3 |
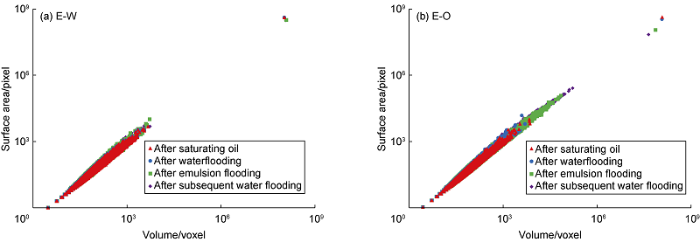
The relationship curves between surface area and volume of development phase in each displacement stage are drawn (Fig. 10) to reveal the changes of remaining oil topological structure. The surface area has a power-law relationship with its volume (Table 3). The fitting results show that the exponent and coefficient of each stage are similar, the exponent is about 1.174 and the coefficient is about 0.265. Eq. 5 is established to estimate the development phase surface area and volume:
Fig. 10.
Fig. 10.
Relationship between development phase surface area and volume.
Table 3 Parameters of power law fitting formula of the relationship between development phase surface area and volume.
| Experimental stage | E-W group | E-O group | ||||
|---|---|---|---|---|---|---|
| Coefficient | Power exponent | R2 | Coefficient | Power exponent | R2 | |
| After saturating oil | 0.263 7 | 1.174 3 | 0.996 7 | 0.265 1 | 1.174 8 | 0.997 2 |
| After waterflooding | 0.263 6 | 1.174 6 | 0.996 7 | 0.263 8 | 1.177 6 | 0.997 1 |
| After emulsion displacement | 0.257 2 | 1.188 7 | 0.996 4 | 0.267 5 | 1.169 4 | 0.997 6 |
| After subsequent water flooding | 0.257 5 | 1.187 6 | 0.996 5 | 0.264 7 | 1.174 6 | 0.997 6 |
3. Microscopic displacement mechanism of emulsion
Three-dimensional reconstruction of microscopic remaining oil images of each displacement stage in E-W group (Fig. 11) intuitively confirms two mechanisms of EOR by emulsion flooding: (1) The blocking effect of emulsion makes the subsequent fluid flow around, and mobilizes the remaining oil in unswept pores (the blue dotted area). (2) Residual oil detaches from rock wall under low interfacial tension system (green dotted line area). Emulsion flooding can simultaneously enlarge pore sweep area and improve oil displacement efficiency at pore-scale. Image processing method is employed to further quantitatively analyze the remaining oil mobilization effect by emulsion flooding: Extract and number the pore structure after scanning the dry core; Superimpose the data of development phase and pore at each flooding stage, and calculate the development phase saturation in different stages; Define the pore whose oil saturation has not changed as unswept pores, and the one that has changed as swept pores, so as to analyze the pore sweep scope and oil displacement efficiency.
Fig. 11.
Fig. 11.
Three-dimensional reconstruction of microscopic residual oil in each displacement stage of E-W group.
3.1. Oil displacement efficiency and sweep scope at pore-scale
The average oil saturation of pores in each statistical interval is counted and calculated (Eq 6). By analyzing the change of average oil saturation in each stage, the swept and unswept pores are distinguished.
In order to further clarify the relationship between displacement efficiency and pore size in each stage, the displacement efficiency is defined as the average pore displacement efficiency in a certain diameter range. The calculation formula is as follows:
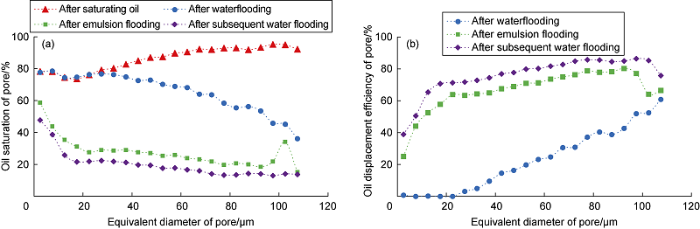
Similarly, with 5 μm as the step size, the statistical interval is divided, and the relationship between the above two parameters and the equivalent pore diameter in each interval of E-W group is calculated (Fig. 12). In the process of saturating oil, the oil saturation is positively correlated with the pore equivalent diameter, that is, the oil phase tends to enter large pores, and the bound water mainly occurs in small pores, which is related to the water-wet nature of the core itself. In water flooding stage, for the pores with equivalent diameter of 30-110 μm, the flooding efficiency is positively correlated with the equivalent diameter. However, the pores with equivalent diameter of 0-25 μm is basically not affected by water flooding, indicating that the injected water in this stage mainly flows along large pores, and the average oil displacement efficiency is 22.9%. In the emulsion flooding stage, the blocking effect of emulsion effectively improves the average oil displacement efficiency in all statistical intervals, and which shows a large upward trend in pores less than 25 μm. Emulsion plugging at the pore throat leads to the change of fluid flow direction, which significantly improves the ability of water phase to enter small pores, indicating the importance of matching emulsion with pore size. In the subsequent water flooding stage, due to the effective retention of emulsion, the injected water further mobilizes the residual oil, and the average oil displacement efficiency at the pore-scale increases from 66.5% to 75.8%.
Fig. 12.
Fig. 12.
Relationship between oil saturation (a), oil displacement efficiency (b) at pore scale and pore equivalent diameter in E-W group.
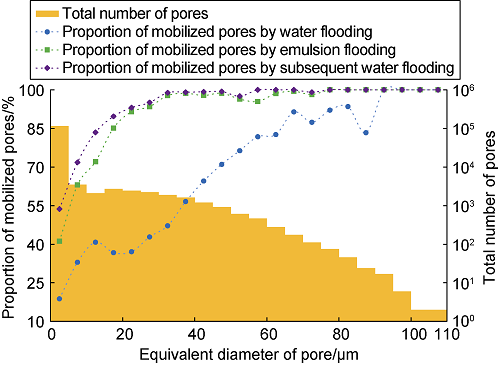
The statistical results of the pores swept by water flooding in E-W group are shown in Fig. 13. After water flooding, a total of 31 039 pores are mobilized, accounting for 23.1% of the total pores (134 497). Due to the selective flow caused by micro-heterogeneity, the oil phase in most pores has not been effectively mobilized in the process of water flooding, and only the pores with the equivalent diameter of 90-110 μm are 100% utilized. The remaining oil in 64 621 pores is mobilized by emulsion flooding, accounting for 48.0% of the total pores. After subsequent water flooding, the remaining oil of 79 709 pores is mobilized, accounting for 59.3% of the total pores, which significantly increases the number of pores in all statistical intervals. And more than 90% of the pores with the equivalent diameter in the range of 20-110 μm can be mobilized, which indicates that the blocking effect of emulsion improves the sweep efficiency of small pores. However, for the pores with an average equivalent diameter less than 20 μm, even though the blocking effect caused by emulsion, the driving force of changing fluid flow direction is still not enough to overcome the capillary pressure, and the sweep efficiency is low. After subsequent water flooding, the number of mobilized pores is still less than 70%.
Fig. 13.
Fig. 13.
Relationship between total number of pores, proportion of mobilized pores and equivalent pore diameter.
3.2. Evolution law of microscopic residual oil
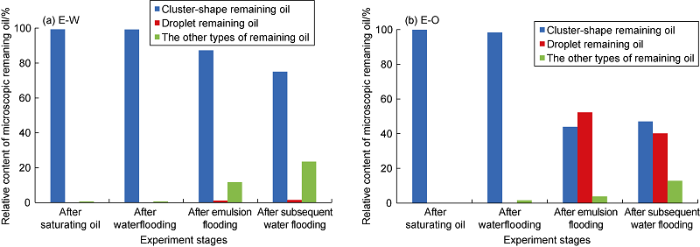
The classification and statistics of microscopic residual oil clarify the main types in displacement process and the research object of subsequent enhanced oil recovery[32,33]. Li et al.[27] divided the remaining oil into five types, namely cluster-shape, multi-porous, columnar, droplet and membranous by considering the shape factor, contact ratio, Euler number and other remaining oil characteristic parameters, and the mobilization difficulty increases in turn. According to this standard, the development phase is also classified. The relative content of cluster- shape and dripping residual oil accounted for a large proportion, while the other three types account for less than 10% in the two groups, so they are collectively referred to as other remaining oil (Fig. 14).
Fig. 14.
Fig. 14.
The relative content of different types of microscopic remaining oil.
In the process of saturating oil and water flooding stage, the difference of remaining oil morphology between the two groups is very small, and the cluster-shape remaining oil is more than 98%, indicating that the parallel experimental design has a good rationality. The development phases of E-O group are oil and emulsion, and the morphology statistics of microscopic remaining oil include the residual oil in the core and the oil phase in trapped emulsion. However, the development phase of E-W group is only oil phase, and it only counts the residual oil in the core. In emulsion flooding, the microscopic remaining oil transforms from continuous to discontinuous, the relative content of the cluster-shape decreases, and the droplet increases (Fig. 14b). The proportion of the droplet in E-O group and E-W group is 52.3% and 1.0%, respectively, which means the droplet in E-O group is mainly the oil phase in trapped emulsion. And it is identified as spherical due to the blocking effect in the process of pore-scale flow. This is consistent with the previous understanding of emulsion occurrence state in porous media[34]. In the heterogeneous core, the remaining oil types after emulsion flooding are mainly the partially unswept cluster-shape remaining oil and the oil phase in emulsion. In the process of subsequent water flooding, some emulsions will deform, flow, coalescence, and the ability to block the pore throat is reduced. The emulsion in this process is continuously produced, and the relative content of oil phase in the trapped emulsion decreases. After subsequent water flooding, the cluster-shape accounts for 47.0% of the remaining oil in the whole core, the oil phase in trapped emulsion accounts for 40.2%, and the other types of remaining oil makes up 12.8%. From the engineering practice of EOR such as surfactant flooding, alkaline water flooding and ASP flooding, the oil phase in the in-situ formed emulsion is an important part of the output[35,36,37]. For the reservoir after emulsion flooding, the main targets of subsequent EOR are cluster-shape remaining oil and the oil phase in trapped emulsion.
4. Conclusions
Emulsion is spherical in real cores, and its sphericity is significantly different from that of other types of remaining oil. Thus the sphericity can be selected as a characteristic parameter to identify and analyze emulsions.
For pores with equivalent diameters of 30 - 55 μm, the average particle size of the emulsion which can be effectively trapped and play the role of conformance control is about 15-25 μm, that is, the emulsion with specific size tends to be trapped in the pore with the matching size. When emulsion volume is smaller than the product of the lower limit of pore occupancy and the corresponding pore volume, it will not be effectively trapped in the pores to achieve the aim of conformance control. In the process of emulsion flooding, it is necessary to design emulsion with suitable particle size according to the pore distribution of the reservoir.
Emulsion flooding plays an important role in improving oil displacement efficiency and expanding pore sweep area. In this paper, through the emulsion adjustment and displacement, the proportion of the number of mobilized pores increases from 23.1% to 59.3% after subsequent water flooding, and the average oil displacement efficiency rises from 22.9% to 75.8%, which significantly improves the microscopic selective flow caused by pore throat heterogeneity and enhances oil recovery. After emulsion flooding, the oil phase trapped in the emulsion accounts for 40.2% of the remaining oil in the whole core, and the cluster-shape makes up 47.0%. Therefore, these two types of remaining oil are the main targets of subsequent EOR.
Nomenclature
dlim—lower limit of emulsion diameter, μm;
D—pore diameter, μm;
Ei—pore displacement efficiency in the ith equivalent diameter interval,%;
i—number of pore equivalent diameter interval, dimensionless;
Ni—number of pores in the ith equivalent diameter interval, dimensionless;
R—correlation coefficient, dimensionless;
S—surface area of development phase, pixel;
Sep—pore occupancy, %;
Sep,lim—the lower limit of pore occupancy,%;
So—surface area of single development phase, pixel;
So,I—average oil saturation in the ith equivalent diameter interval at pore-scale, dimensionless;
So,I—average oil saturation of pores in the ith equivalent diameter interval at initial state, dimensionless;
${{S}_{o,{{N}_{i}}}}$—oil saturation of the Nith pore in the ith equivalent diameter interval, dimensionless;
V—volume of development phase, voxel;
${{V}_{{{N}_{i}}}}$—pore volume of the Nith pore in the ith equivalent diameter interval, μm3;
Ve—sum of gray data voxels in pores, voxel;
Ve,3d—sum of emulsion voxels in pores, voxel;
Vo—volume of single development phase, voxel;
Vo,3d—sum of oil phase voxels in pores, voxel;
Vw,3d—sum of water phase voxels in pores, voxel;
V3d—sum of pore voxels, voxel;
θ—sphericity, dimensionless.
Reference
Effects of pore structure on surfactant/polymer flooding-based enhanced oil recovery in conglomerate reservoirs
Experimental study on surface-active polymer flooding for enhanced oil recovery: A case study of Daqing placanticline oilfield, NE China
Integrated hydraulic fracturing techniques to enhance oil recovery from tight rocks
Influences of the strong-base ASP system on the mineral components of the reservoirs
Investigation of gravity-stable surfactant floods
DOI:10.1016/j.fuel.2014.01.082 URL [Cited within: 2]
Emulsions: Theory and practice
Experimental study on a fine emulsion flooding system to enhance oil recovery for low permeability reservoirs
DOI:10.1016/j.petrol.2018.08.011 URL [Cited within: 1]
Formation damage during alkaline-surfactant-polymer flooding in the Sanan-5 block of the Daqing Oilfield, China
DOI:10.1016/j.jngse.2016.07.046 URL [Cited within: 1]
Dynamic flow response of crude oil-in-water emulsion during flow through porous media
DOI:10.1016/j.fuel.2014.06.025 URL [Cited within: 1]
Emulsion flooding for enhanced oil recovery: Filtration model and numerical simulation
DOI:10.1016/j.petrol.2016.02.018 URL [Cited within: 1]
Heavy-oil recovery by in-situ emulsion formation
DOI:10.2118/129914-PA URL [Cited within: 1]
Features and imbibition mechanisms of Winsor Ⅰ type surfactant solution in oil-wet porous media
Application of microfluidic models in the oil and gas field development
Pore scale dynamics of microemulsion formation
DOI:10.1021/acs.langmuir.6b00821 URL [Cited within: 1]
The influence of salinity and mineral components on spontaneous imbibition in tight sandstone
DOI:10.1016/j.fuel.2020.117087 URL [Cited within: 1]
Role of chemical additives on water-based heavy oil mobilization: A microfluidic approach
DOI:10.1016/j.fuel.2018.12.099 URL [Cited within: 1]
Flow physics of polymer nanospheres and diluted microemulsion in fractured carbonate reservoirs: An investigation into enhanced oil recovery mechanisms
DOI:10.2118/205381-PA URL [Cited within: 1]
Formation and flow behaviors of in situ emulsions in heavy oil reservoirs
DOI:10.1021/acs.energyfuels.9b00154 URL [Cited within: 1]
A 2.5-D glass micromodel for investigation of multi-phase flow in porous media
DOI:10.1039/c6lc01476c
PMID:28157240
[Cited within: 1]

We developed a novel method for fabrication of glass micromodels with varying depth (2.5-D) with no additional complexity over the 2-D micromodels' fabrication. Compared to a 2-D micromodel, the 2.5-D micromodel can better represent the 3-D features of multi-phase flow in real porous media, as demonstrated in this paper with three different examples. Physically realistic capillary snap-off and the formation of isolated residual oil droplets were realized, which is not possible in 2-D micromodels. Droplet size variation during an emulsion flooding was investigated on the 2.5-D micromodel, showing that the droplet size decreases sharply at the inlet, with little change in size downstream of the micromodel. Displacement of light oil with ultra-low interfacial tension (IFT) surfactant was conducted in the 2.5-D micromodel, where we were able to visualize the generation and flowing of a microemulsion phase, which agrees with, and explains observations in experiments of more complex porous media.
A multi-scale experimental study of hydrophobically-modified polyacrylamide flood and surfactant-polymer flood on enhanced heavy oil recovery
DOI:10.1016/j.petrol.2019.106258 URL [Cited within: 2]
New insights into flow physics in the EOR process based on 2.5D reservoir micromodels
DOI:10.1016/j.petrol.2019.106214 URL [Cited within: 1]
Enhancement of oil recovery by emulsion injection: A pore scale analysis from X-ray micro-tomography measurements
DOI:10.1016/j.petrol.2020.108134 URL [Cited within: 1]
The critical factors for permeability-formation factor relation in reservoir rocks: Pore-throat ratio, tortuosity and connectivity
DOI:10.1016/j.energy.2019.116051 URL [Cited within: 1]
Using pressure pulse decay experiments and a novel multi-physics shale transport model to study the role of Klinkenberg effect and effective stress on the apparent permeability of shales
DOI:10.1016/j.petrol.2020.107010 URL [Cited within: 1]
Effects of microscopic pore structure heterogeneity on the distribution and morphology of remaining oil
Pore-scale investigation of microscopic remaining oil variation characteristics in water-wet sandstone using CT scanning
Pore-scale study of the pressure-sensitive effect of sandstone and its influence on multiphase flows
DOI:10.1007/s12182-018-0266-6
[Cited within: 2]

The pressure-sensitive effect on the pore structure of sandstone was investigated using X-ray computed micro-tomography and QEMSCAN quantitative mineral analysis. In a physical simulation study, we extracted the pore network model from digital cores at different confining pressures and evaluated the effect of pressure sensitivity on the multiphase displacement process. In both the pore network model and QEMSCAN scanning, the pore structure was observed to be damaged under a high confining pressure. Due to their different scales, the pores and throats exhibited inhomogeneous changes; further, the throats exhibited a significant variation compared to that exhibited by the pores. Meanwhile, the heterogeneity of the pore structure under the two aforementioned activities was aggravated by the elastic-plastic deformation of the pore structure. The pressure-sensitive effect increased the proportion of mineral particles, such as quartz (the main component of the core skeleton), and reduced the proportion of clay minerals. The clay minerals were originally attached to the pore walls or interspersed in the pores; however, as the pressure increased, the clay minerals accumulated in the pores resulting in blockage of the pores. While simulating the multiphase displacement process, increasing the confining pressure was observed to severely restrict the flowability of oil and water. This study promises to improve the efficiency of reservoir development in terms of oil and gas exploitation.
Effect of pore structure on displacement efficiency and oil-cluster morphology by using micro computed tomography (mu CT) technique
DOI:10.1016/j.fuel.2018.05.058 URL [Cited within: 1]
Relative permeabilities from two- and three-dimensional pore-scale network modelling
Comparison of residual oil cluster size distribution, morphology and saturation in oil-wet and water-wet sandstone
DOI:10.1016/j.jcis.2012.02.025 URL [Cited within: 1]
Simultaneous oil recovery and residual gas storage: A pore-level analysis using in situ X-ray micro-tomography
DOI:10.1016/j.fuel.2012.06.094 URL [Cited within: 1]
The residual oil in Es2 reservoir, south area of Pucheng Oilfield
Law of pore structure variety in reservoir during a long episode waterflooded development
Emulsions in porous media: From single droplet behavior to applications for oil recovery
DOI:10.1016/j.cis.2018.03.002 URL [Cited within: 1]
Technologies of enhancing oil recovery by chemical flooding in Daqing Oilfield, NE China
Current development and application of chemical combination flooding technique
Pore-level visual analysis of heavy oil recovery using chemical-assisted waterflooding process: Use of a new chemical agent
DOI:10.1016/j.fuel.2018.10.104 URL [Cited within: 1]