China is very rich in unconventional oil and gas resources. The recoverable resources of tight (shale) oil, tight gas and shale gas in China account for 9.7%, 5.7% and 4.8% of global recoverable resources, respectively^[1]. Unconventional oil and gas reservoirs are low in porosity and permeability. Conventional water-based drilling fluid and fracturing fluid would cause damage to these reservoirs, while supercritical carbon dioxide (SC-CO₂) would not, so SC-CO₂ can be used as anhydrous drilling fluid and fracturing fluid for efficient recovery of unconventional oil and gas to increase the oil and gas production, save water resources, reduce energy consumption and carbon emission. Relevant application technologies include SC-CO₂ jet drilling^[2] and SC-CO₂ jet fracturing^[3].

SC-CO₂ has a viscosity of 0.02 mPa·s at 8 MPa and 50°C, and 0.07 mPa·s at 20 MPa and 50 °C, only 1/10 less than that of water-based drilling fluid, so SC-CO₂ has low circulating pressure loss, which avoids clay expansion and water lock effect, and damages to reservoirs. SC-CO₂ has the density sensitive to the wellhead back pressure, 220 kg/m³ at 8 MPa and 50 °C and 758 kg/m³ at 20 MPa and 50 °C, so underbalanced drilling conditions can be reached more easily^[4]. Compared with other drilling fluids such as nitrogen and foam, SC-CO₂ can reach a higher density close to water, and provide enough torque for downhole motor^[5,6]. In addition, threshold pressures breaking granite and shale of SC-CO₂ jet are 1/3 and 1/2 of that of water jet respectively at the jet pressure difference of 55-193 MPa^[6]. Because of the above characteristics, SC-CO₂ jet drilling has higher rate and lower cost^[6,7,8,9].

Compared with hydraulic fracturing, SC-CO₂ jet fracturing has larger perforation and static pore pressure and can make fracture initiate and propagate at a lower pressure^[3], and with fracture initiation pressure 50% less than that of hydraulic fracturing^[10]. The temperature stress caused by temperature drop during CO₂ flow in the fractures would facilitate the formation of complex fracture network around the main fracture^[11], and the strength of rock in contact with CO₂ decreases^[12]. Particularly, SC-CO₂ jet fracturing is suitable for the exploitation of shale gas in China. Shale has low permeability and porosity and high clay content; and shale gas reservoirs are widely distributed in the regions with water shortage in China and have low production when fractured with water-based fracturing fluid^[13]. Using SC-CO₂ as fracturing fluid can solve the problems of clay hydration and water shortage, and this fracturing fluid has hardly residual left in reservoir, thereby no damage to reservoir permeability; moreover, CO₂ can displace the methane and realize geological sequestration of CO₂ as shale has higher adsorption ability to CO₂^[14,15,16].

So far, a large number of experimental studies both at home and abroad have proved that SC-CO₂ jet has more advantages than water jet in rock-breaking. Kolle et al.^[6,7] proved through experiment that SC-CO₂ jet had specific energy consumption 50% less than that of water jet in rock-breaking. Tian, Huang, Du and Wang et al.^{[5, 17-19]} found the shale broke in large pieces in grid-like pattern using SC-CO₂ jet, and influences of jet temperature, jet pressure, and standoff distance on rock-breaking by SC-CO₂ jet. SC-CO₂, with low viscosity and high density, can transfer pressure rapidly in pores and fractures. However, there is no further quantitative study on its rock-breaking mechanism. Li et al.^[20,21,22] found that the rock surface impacted by SC-CO₂ jet field dropped dozens of degrees in temperature, resulting in large temperature gradient and temperature stress. Thus, higher temperature stress is the key factor why SC-CO₂ jet has better rock-breaking performance, lower threshold pressure, and larger rock breaking area than water jet.

Rock-breaking by jet is a process in which rocks are eroded layer by layer with increase of jet standoff distance. The variations of pressure and temperature with standoff distance determine the threshold pressure, rock-breaking area and rock-breaking depth. But previous experiment on the influence of temperature stress on rock-breaking by SC-CO₂ jet were done at constant standoff distance^[20,21,22]; and rarely covered changes of jet field and rock stress with standoff distance, so the reasons why SC-CO₂ jet has larger rock-breaking depth than water jet and results in bulk rock breaking remain evasive. Experiments of SC-CO₂, water and nitrogen jet rock-breaking were conducted in this work to compare the flow fields and rock stresses at different standoff distances and reveal the heat-fluid-solid coupling mechanism of rock-breaking by SC-CO₂ jet, in the hope to provide a theoretical basis for the development and application of SC-CO₂ jet drilling and SC-CO₂ jet fracturing.

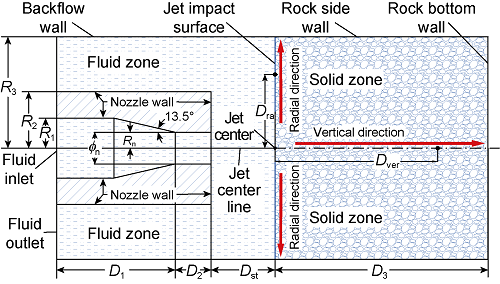
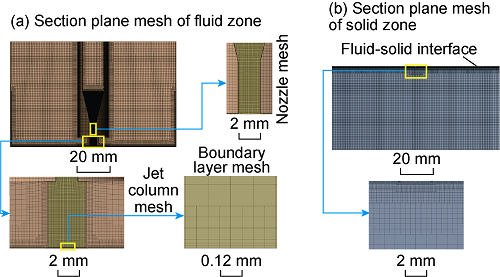
A full-scale physical model was established (Fig. 1) based on experimental equipment^[18] with the standoff distance D_st of 2-100 mm, rock radius R₃ and length D₃ of 50 mm and 100 mm respectively, nozzle outlet radius, R_n of 1 mm, and inlet inner and outer diameters, R₁ and R₂, of 6.5 mm and 11.5 mm, respectively. The lengths of contraction surface in front of the orifice of nozzle outlet, D₁, and orifice D₂, were 100 mm and 10 mm long respectively. D_ra was defined as the radial distance from a point on rock surface to the jet center; D_ver was defined as the vertical distance from a point at the axis in the rock to the jet center; D_ra/R_n was dimensionless radius; and D_ver/ϕ_n was dimensionless depth. In order to better capture the fluctuations of temperature, velocity and pressure, Cartesian mesh refined in local parts was used in griding the model (Fig. 2), with the average quality of about 0.98 (1 represents the best quality).

(1) The process of fluid flowing through nozzle was adiabatic due to the small heat transfer between fluid and nozzle wall; (2) the permeability of rock wasn’t considered in the simulation due to the small impact of flow on rock- breaking by jet^[23]; (3) the influence of rock deformation on flow field was neglected as the rock deformation is less than the surface roughness of most rocks at the jet pressure difference of 60 MPa; (4) the rock was assumed as a homogeneous medium because different thermal expansion coefficient and temperature gradient are the main reasons of rock-breaking^{[24,25,26,27]} and rock heterogeneity set artificially would exaggerate the temperature stress.

The flow field was calculated by Fluent software. Realizable k-ε turbulence model can effectively calculate the rotating shear flow, jet, boundary layer flow, and separated flow, etc.^{[28,29,30,31,32,33,34]}. The implicit equation recommended by NIST (National Institute of Standards and Technology) was used to describe the pressure, temperature, viscosity and thermal conductivity of carbon dioxide^[35], nitrogen^[36] and water^[37].

The specific heat capacity is calculated according to the formula below:

The viscosity of carbon dioxide and nitrogen is calculated according to the formula below^[38,39]:

The thermal conductivity of carbon dioxide and nitrogen is calculated according to the formula below:

The viscosity and thermal conductivity of water are calculated according to the formulas below^[40]:

In this paper, the static elastic failure theory was adopted, i.e. the rock mainly undergoes tensile failure and shear failure under jet impact. The dynamic rock-breaking process mainly includes three steps. Step 1 is that the rock produces initial crack under the jet impact. Step 2 is that the jet further expands the crack through water wedge effect. Step 3 is that the broken rock is eroded. As the above process is repeated, both the standoff distance and rock-breaking depth increase.

The static structural module of ANSYS was used to calculate the stress. The governing equations of rock mechanics and heat conduction are as follows.

The relationship between stress and strain is as follows:

The heat conduction equation is as follows:

Based on investigation of the mechanical and thermodynamic properties of rock^{[41,42,43,44,45,46]}, the hard rock in the simulation had a density of 2.55×10³ kg/m³, specific heat capacity of 1 kJ/(kg·K), thermal conductivity of 1.8 W/(m·K), Poisson ratio of 0.15, elastic modulus of 70 GPa, and thermal expansion coefficient of 15×10^-6 K^-1.

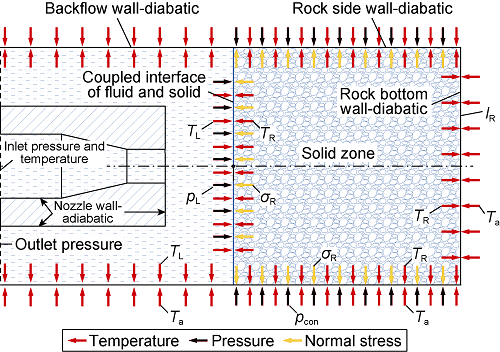
The boundary conditions of inlet pressure, temperature and outlet pressure were set in the simulation (Fig. 3). The nozzle wall was set as adiabatic, and other boundary conditions were set as shown in Eqs. (9)—(11).

The boundary conditions of rock sidewall and bottom were as follows:

The boundary conditions of fluid and rock interface were as follows:

(1) The boundary conditions of fluid inlet and outlet were set, and the temperature and pressure fields of the jet at a steady state were calculated with the heat transfer between fluid and rock not taken into account. (2) The heat transfer between fluid and rock was taken into account, the pressure field on the rock surface and the temperature field inside the rock at t_j were calculated by taking the flow field in step (1) as the initial condition and zero time. (3) By taking the pressure field on the rock surface and temperature field inside the rock obtained in step (2) as the initial conditions, the bottom boundary of the rock was set at zero displacement, and the pressure on the side of the rock was set at 10 MPa, the tensile stress and shear stress on the rock at t_j were calculated.

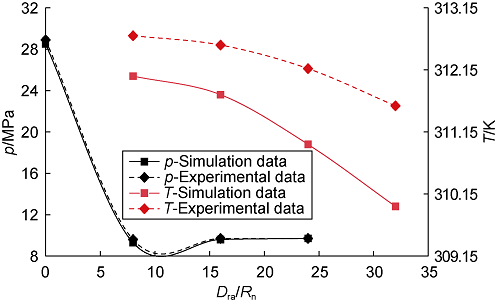
The experimental data at the dimensionless standoff distance (D_st/ϕ_n) of 2 was used to validate the flow field simulation method. During the test, the pressure was directly measured by the pressure sensors on the test panel, and the temperature was indirectly measured by the temperature sensors in the protective cover on the test panel. The pressure sensors were placed at the dimensionless radii (D_ra/R_n) of 0, 8, 16 and 24, and the temperature sensors were placed at the dimensionless radii of 8, 16, 24 and 32 respectively. The test was carried out at T_in=300.15 K, p_in=30.3 MPa, T_a=287.95 K, and p_out=9.6 MPa. As the jet time would influence heat transfer, so the average values of relatively stable temperature and pressure data after 2 mins of jet were used. Based on the structure of the test panel and the properties of the material, a physical model was built to calculate the pressure distribution and temperature distribution. Fig. 4 shows the temperature distributions and pressure distributions from the simulation and experiment. It can be seen the pressure and temperature from the simulation have an average error below 1% and 2%, respectively, and the simulation results are basically consistent with the experimental results, validating the effectiveness of the flow field calculation method.

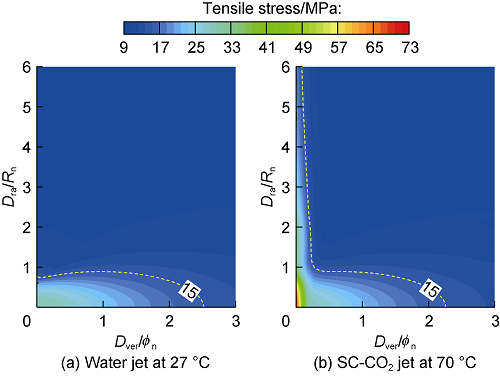
By using the existing experimental data of rock-breaking^{[6, 18]}, the stress field calculation method was verified. SC-CO₂ jet has two obvious characteristics: (1) At constant pressure, the rock broken area and volume by SC-CO₂ jet is twice more than those by water jet; and (2) the threshold pressure p_th of rock-breaking by SC-CO₂ jet is 66.7% below that of water jet. Fig. 5 shows the simulated stress distributions under SC-CO₂ jet and water jet impact at t_j=1 s, p_in=30 MPa, p_out=10 MPa, T_a=343.15 K, D_st/ϕ_n=2. The results show that the maximum tensile stress of water jet was 43% of that of SC-CO₂ jet. Assuming that the tensile strength of rock was 15 MPa, based on the distribution of 15 MPa contour in Fig. 5, the calculated radius and volume of rock-breaking by water jet were 9% and 17% of those of SC-CO₂ jet respectively. The calculated results are basically consistent with the experimental results, validating the effectiveness of the calculation method.

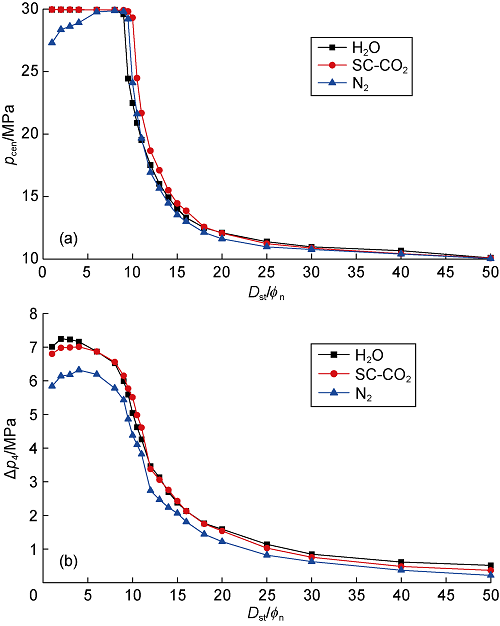
Due to the influence of shock wave^[47], nitrogen jet has lower pressure than water jet and SC-CO₂ jet; SC-CO₂ jet has higher pressure than water jet at the dimensionless standoff distance of 10 and insignificant differences from water jet at other dimensionless standoff distances (Fig. 6). The rock surface pressure on the jet centerline was p_cen, and the average pressure difference between p_cen and outlet pressure (p_out) was Δp₄ at the dimensionless radius (D_ra/R_n) below 4. With the increase of standoff distance, p_cen decreases under water and SC-CO₂ jets and first increases and then decreases under nitrogen jet (Fig. 7a); Δp₄ increases first and then decreases under water, SC-CO₂ and nitrogen jets (Fig. 7b). The stress analysis shows that the maximum jet pressure determines the maximum tensile stress, and the range of high pressure determines the range of high stress area. Therefore, the larger the p_cen, the smaller the threshold pressure of rock-breaking is; the larger the Δp₄, the larger the broken area is. Therefore, p_cen and Δp₄ were used to evaluate the threshold pressure of rock-breaking and broken area. SC-CO₂ jet has smaller threshold pressure of rock-breaking than water jet at the dimensionless standoff distance of 10-15, and similar threshold pressure of rock-breaking with water jet at the dimensionless standoff distances other than 10-15; on the whole, SC-CO₂ jet has similar rock broken area to water jet, this can’t explain the advantages of SC-CO₂ jet over water jet in rock-breaking. The nitrogen jet has smaller rock broken area than water jet and SC-CO₂ jet, indicating that water jet and SC-CO₂ jet have more advantages than nitrogen jet in rock-breaking.

Fig. 8 shows the relationship between temperature distribution on the rock surface and dimensionless standoff distance (D_st/ϕ_n). It can be seen from Fig. 8 that water jet causes the rise of rock temperature, whereas SC-CO₂ and nitrogen jets cause the drop of rock temperature; and SC-CO₂ jet causes the largest temperature difference. In the field drilling, the mass flow rate is 10 times more than that in this case. High flow rate would lead to insufficient heat exchange between the fluid in the drill pipe and the formation, and the fluid temperature at the nozzle inlet is lower than the formation temperature, therefore, the water jet will not cause the rise of temperature on the rock surface in actual working conditions. The jet pressure mainly acts on the area with dimensionless radius below 2, while the jet temperature difference acts on the whole rock surface, affecting an area 20 times more than the area affected by jet pressure.

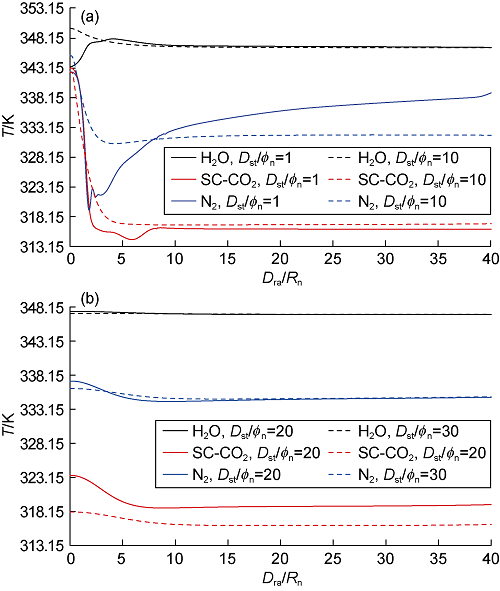
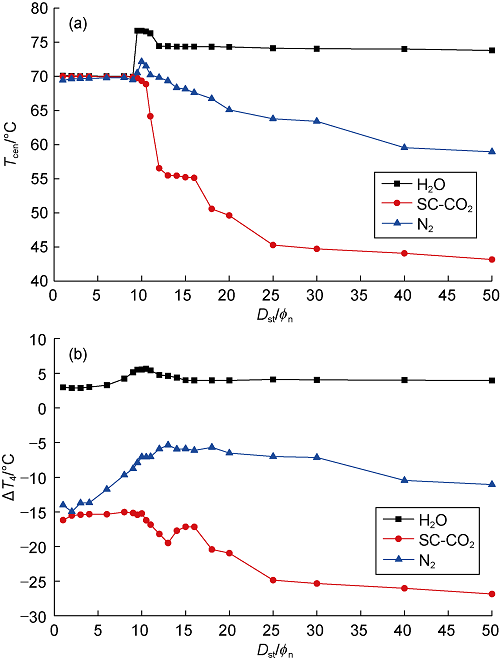
The rock surface temperature on the jet centerline is T_cen, and the average temperature difference between the rock surface temperature and the ambient temperature at the dimensionless radius (D_ra/R_n) below 4 is ΔT₄. Fig. 9 shows the curves of the temperature at jet centerline and average jet temperature difference versus dimensionless standoff distance. The variation of jet temperature with standoff distance is more complicated due to the dual effects of heat generation during turbulence and heat absorption during expansion. The overall trend shows that with increasing standoff distance, ΔT₄ increases (the absolute value increases) under SC-CO₂ jet, first decreases (absolute value decreases) and then increases under nitrogen jet and increases slightly under water jet. At the standoff distance (D_st/ϕ_n) above 10, ΔT₄ under SC-CO₂ jet is more than 5 times and 2.5 times of that under water jet and nitrogen jet, respectively, while the pressures of SC-CO₂, nitrogen and water jets drop significantly. The existing research results show that both increase and decrease of the jet temperature would cause the rock stress to increase. Therefore, it is the temperature stress caused by jet temperature difference that makes SC-CO₂ jet have larger broken area and depth than water and nitrogen jets, which is consistent with the experimental results at constant standoff distance^[6,7]. With the increase of standoff distance, the contribution of temperature difference to rock stress increases under SC-CO₂ jet.

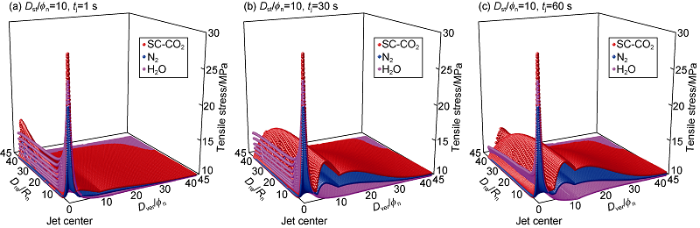
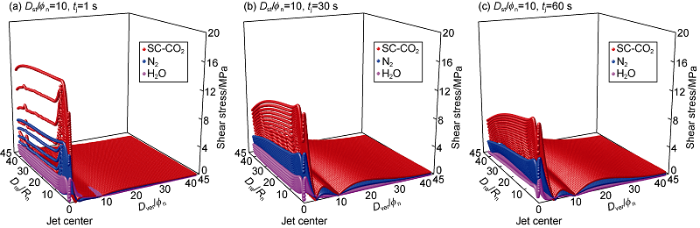
Fig. 10 and Fig. 11 show the variations of rock stresses with jet time in temperature and pressure coupling fields at the dimensionless standoff distance (D_st/ϕ_n) of 10. It can be seen that with the increase of jet time, both the tensile stress and shear stress (D_ver/ϕ_n=0, 0<D_ra/R_n<40) on the rock surface decrease and the internal tensile and shear stress (D_ver/ϕ_n>0, 0<D_ra/R_n<40) in the rock increase; when the jet time is short, water jet has the biggest tensile stress on the rock surface, followed by SC-CO₂ jet; when the jet time is long, SC-CO₂ jet has the biggest tensile stress, followed by water jet; the three kinds of jets have shear stresses in the same sequence regardless of jet time, i.e. SC-CO₂ jet has the largest shear stress, followed by nitrogen jet. On the whole, significant tensile failure and shear failure occur under SC-CO₂ jet impact.

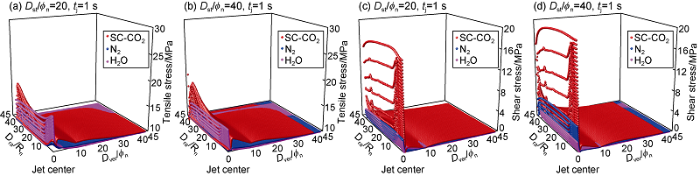
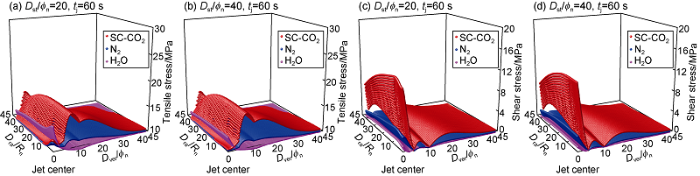
According to the rock stress distribution at the jet time of 1 s and 60 s (Figs. 12 and 13), the influence of standoff distance on rock stress under jet impact was analyzed. With the increase of dimensionless standoff distance from 20 to 40, both the tensile stress and shear stress inside the rock increase under SC-CO₂ and nitrogen jets, but decrease under water jet, indicating that SC-CO₂ jet increases in rock-breaking capability than water jet. With increase of standoff distance, under SC-CO₂ and nitrogen jets, the high stress area transfers from the jet center to the nearby rock surface and into the rock, the pressure decreases (Fig. 7), while the temperature difference increases (Fig. 9), indicating that the contribution of jet temperature field to rock stress increases.

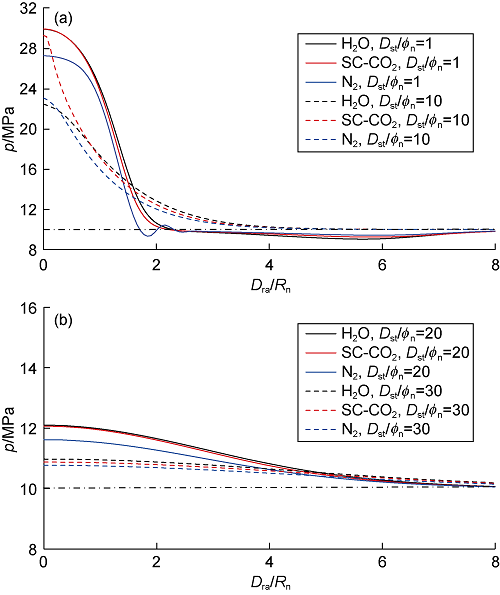
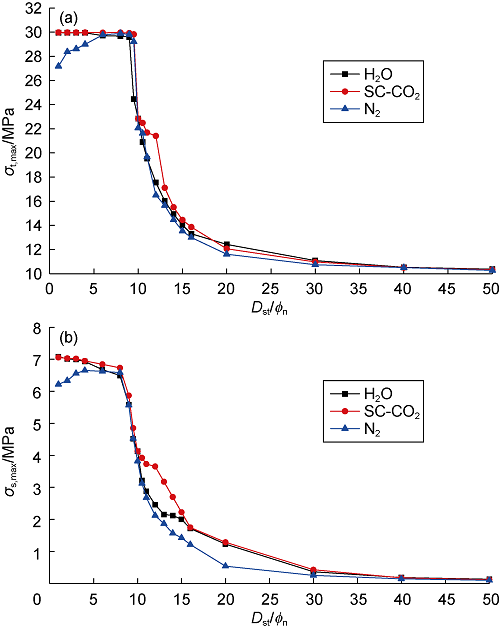
Based on the curve of the maximum stress versus standoff distance, the influence of temperature stress on rock stress was further analyzed. Fig. 14 shows that at the dimensionless standoff distance of 1-6, the rock stress under water and SC-CO₂ jets is larger than that of nitrogen jet; at the dimensionless standoff distance of 11-15, the rock stress is larger under SC-CO₂ jet, but slight rock-breaking advantage than water jet, unable to explain why SC-CO₂ jet has greater rock-breaking depth than water jet.

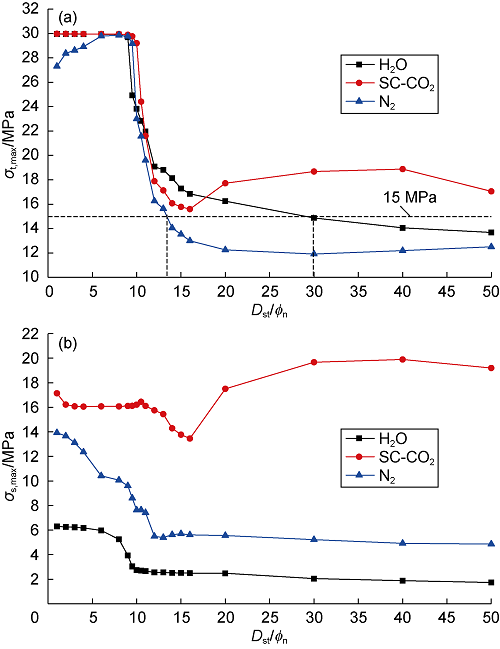
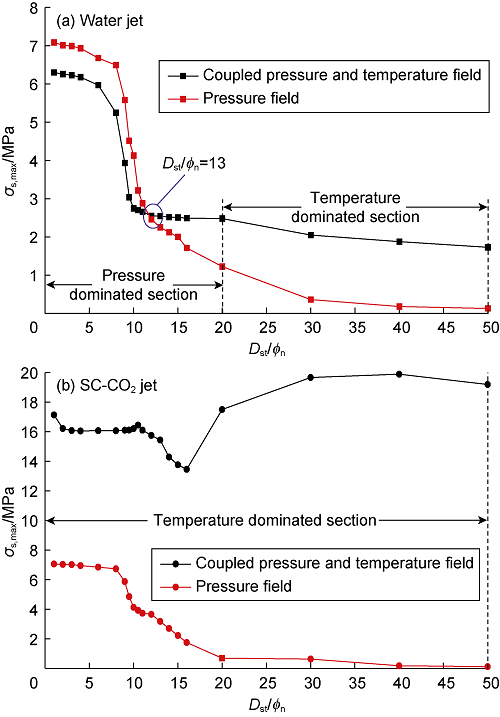
Fig. 15 shows the variations of rock stress with dimensionless standoff distance under the coupled jet-pressure and temperature field. It can be seen from this figure that compared with nitrogen jet, water jet results in larger tensile stress and smaller shear stress on the rock; as the rock fails largely due to tensile stress, water jet has more advantage than nitrogen jet in rock-breaking. SC-CO₂ jet produces larger tensile stress and shear stress on rock than water jet and nitrogen jet; especially at the dimensionless standoff distances of 20-50, the maximum tensile stress under SC-CO₂ jet is over 1.3 times and 1.5 times than that under water jet and nitrogen jet, respectively, and the maximum shear stress under SC-CO₂ jet is over 6 times and 3 times than that under water jet and nitrogen jet respectively, indicating that SC-CO₂ jet is more likely to produce combined tensile failure and shear failure under the coupled pressure and temperature field. If the rock has a tensile strength of 15 MPa, SC-CO₂ jet, water jet and nitrogen jet have effective dimensionless standoff distances of over 50, 30 and 13 respectively, indicating that the temperature stress is the reason why SC-CO₂ jet has greater rock-breaking depth than water jet.

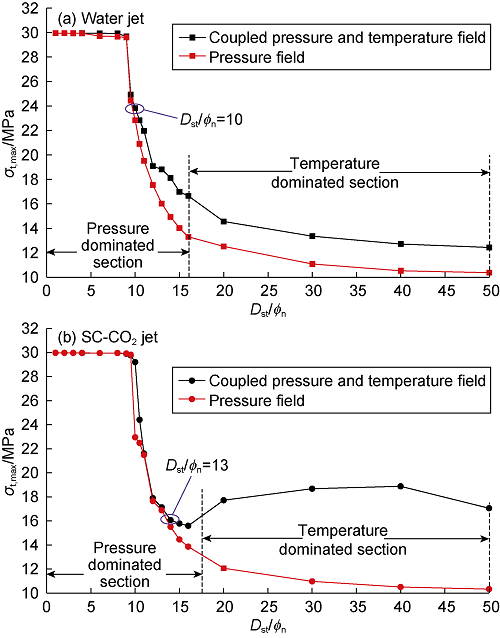
Comparison of the maximum tensile stresses and shear stresses under pressure field and coupled pressure-temperature field with dimensionless standoff distance (Figs. 16 and 17) shows that jet temperature field makes the tensile stress on rock under water jet and SC-CO₂ jet increase at the dimensionless standoff distance of 10 and 13, respectively, and the temperature stress begins to play a dominant role at the dimensionless standoff distance of about 16, so the curve of tensile stress on rock versus standoff distance can be divided into two sections: pressure dominated section and temperature dominated section. The jet temperature field has quite different effect on shear stress and tensile stress on rock. Under water jet, the jet temperature field makes the shear stress on rock decrease at the dimensionless standoff distance below 13, but increase at the dimensionless standoff distance above 13. Under SC-CO₂ jet, the temperature field makes the shear stress on rock increase by 2.3 times at least. The shear stress is mainly produced by the temperature stress. With the variations of standoff distance, there is no pressure dominated zone under SC-CO₂ jet.

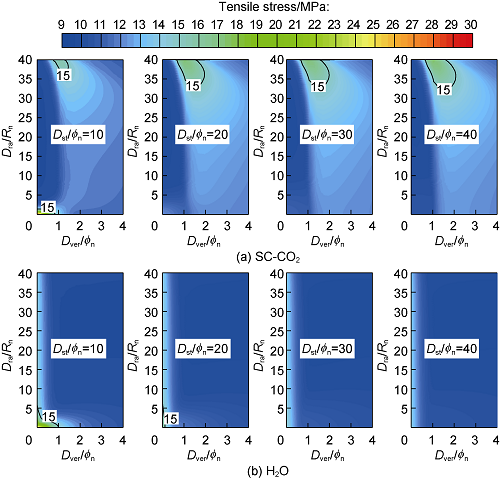
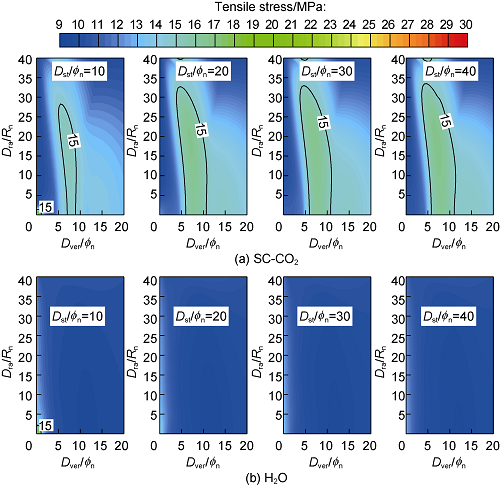
The variations of tensile failure area with dimensionless standoff distance at jet time of 1 s and 60 s with the rock tensile strength of 15 MPa are show in Fig. 18 and Fig. 19. It can be seen that the water jet mainly damages the jet center (origin 0) and nearby rocks; with the increase of jet time, the tensile broken area decreases, indicating that the rock is mainly eroded layer by layer in a short time under water jet. The SC-CO₂ jet not only damages the rock in the jet center and nearby, but also the inside of the rock; with the increase of jet time, the area of internal tensile broken area increases, indicating that the rock is not only eroded layer by layer in short time, but also has volume damage inside in longer time, so SC-CO₂ jet has higher rock-breaking efficiency than water jet. SC-CO₂ jet has larger broken area than water jet and increases the broken area by more than 15 times at the dimensionless standoff distance of 10. With the increase of standoff distance and jet time, this advantage of SC-CO₂ jet becomes even more remarkable.

With the increase of standoff distance, the pressure on the rock surface under nitrogen jet is smaller than that under water jet and SC-CO₂ jet; at the dimensionless standoff distance above 10, the average temperature difference on the rock surface under SC-CO₂ jet is about 2.5 times and over 5 times than that under nitrogen jet and water jet, respectively. Different from jet pressure that acts only near the rock jet centerline, the SC-CO₂ jet temperature difference acts on the whole rock surface. Therefore, SC-CO₂ jet can produce larger area and depth of rock-breaking than water and nitrogen jets. Temperature stress is the reason why SC-CO₂ jet has more advantage than water and nitrogen jets in rock-breaking. The jet pressure plays a main role in rock-breaking at smaller standoff distance, whereas jet temperature difference plays a main role in rock-breaking at larger standoff distance. Under SC-CO₂ jet, tensile stress and shear stress on rock are stronger than that under water jet and nitrogen jet, so rock is more likely to have bulk failure, and rock-breaking advantage of SC-CO₂ jet increases with the increase of standoff distance.

Under limited surface pumping pressure, underbalanced drilling can produce larger jet pressure difference and temperature difference; pulse jet and swirling jet can also increase the pressure and temperature gradients on the rock surface through high-frequency pulsation. All the measures can improve the coupling heat-fluid-solid rock-breaking effect of SC-CO₂ jet.

C—specific heat capacity of rock, J/(kg·K);

C_p—specific heat capacity at constant pressure, J/(kg·K);

D_ra—radial distance from a point on the rock surface to the jet centerline, mm;

D_ra/R_n—dimensionless radius;

D_st—distance between nozzle and rock surface, mm;

D_st/ϕ_n—dimensionless standoff distance;

D_ver—vertical distance from a point on the axis inside the rock to the jet centerline, mm;

D_ver/ϕ_n—dimensionless depth;

D₁—length of the contraction surface in font of nozzle orifice, mm;

D₂—length of nozzle orifice, mm;

D₃—rock length, mm;

E—modulus of elasticity, Pa;

k—kinetic energy of turbulence, J;

l_R—displacement of rock bottom, m;

M—relative molecular weight, kg/mol;

p—pressure, Pa;

p_cen—rock surface pressure on the jet centerline, MPa;

p_con—confining pressure on rock, Pa;

p_in—fluid pressure at the nozzle inlet, MPa;

p_L—fluid pressure at interface, Pa;

p_out—fluid pressure at the outlet, MPa;

p_th—threshold rock-breaking pressure of the jet, MPa;

q_v—heat generation rate, J/(m³·s);

R—gas constant, J/(mol·K);

R₁—inner diameter of nozzle inlet, mm;

R₂—outer diameter of nozzle inlet, mm;

R₃—rock radius, mm;

R_n—radius of nozzle outlet, mm;

t—time, s;

t_j—jet time, s;

T—temperature, K;

T_a—ambient temperature, K;

T_cen—rock surface temperature on the jet centerline, °C;

T_in—inlet temperature, K;

T_L—fluid temperature at interface, K;

T_R—rock temperature at interface, K;

T₀—initial rock temperature, K;

x, y, z—three directions in rectangular coordinates;

α—coefficient of thermal expansion, K^-1;

δ—ratio of density to critical density, dimensionless;

Δp₄—average pressure difference between rock surface pressure and outlet pressure at the D_ra/R_n below 4, MPa;

ΔT₄—average temperature difference between rock surface temperature and ambient temperature at the D_ra/R_n below 4, °C;

Δλ—increment of heat conductivity caused by the density increase of thinner gas at constant temperature, W/(m·K);

Δλ_c—increment of heat conductivity near the critical point, W/(m·K);

Δμ—increase of viscosity caused by the density increase of thinner gas at constant temperature, Pa·s;

Δμ_c—increase of viscosity near the critical point, Pa·s;

ε—dissipation rate of turbulence kinetic energy, dimensionless;

ε_ii—strain in Direction i, dimensionless;

λ—heat conductivity, W/(m·K);

λ₀—ultimate heat conductivity at the density close to zero at a certain temperature, W/(m·K);

λ₁—increase rate of heat conductivity caused by the density increase of thinner gas at constant temperature, dimensionless;

μ—viscosity, Pa·s;

μ₀—ultimate viscosity at the density close to zero at a certain temperature, Pa·s;

μ₁—increase ratio of viscosity caused by the density increase of thinner gas at constant temperature, dimensionless;

μ₂—increase rate of viscosity near the critical point, dimensionless;

ν—poisson's ratio, dimensionless;

ρ—density, kg/m³;

σ_ii, σ_jj, σ_kk—stress tensor in three directions on the coordinate, Pa;

σ_R—normal stress on the rock surface, Pa;

σ_s,max—maximum shear stress, MPa;

σ_t,max—maximum tensile stress, MPa;

τ—ratio of temperature to critical temperature, dimensionless;

ϕ_n—diameter of nozzle outlet, mm;

ϕ_δ,r—partial differential of remaining Helmholtz free energy ϕ_r(δ, τ), dimensionless;

ϕ_ττ,o—the second order partial differential of ideal Helmholtz free energy ϕ_o(δ, τ), dimensionless;

ϕ_δτ,r, ϕ_δδ,r, ϕ_ττ,r—the second order partial differential of remaining Helmholtz free energy ϕ_r(δ, τ), dimensionless;

Subscript:

r—Residual;

o—Ideal.