Introduction
As an important unconventional energy source, the efficient exploitation of coal-bed methane has great significance to energy supply and carbon emission reduction[1]. Due to the low strength of the coal seam, it is difficult to keep wellbore stability for a long time under the influence of drilling fluid softening and ground stress during the drilling process. Supercritical CO2 (SC-CO2) is a drilling fluid with a great potential for field application. Compared with conventional water-based drilling fluids, it can avoid wellbore instability and water lock effect caused by “hydraulic” measures. In addition, CO2 can increase the development degree of coal pores and fractures by extractive dissolution with coal matrix, thus improving the permeability of low-permeability coal seams. Moreover, its adsorption efficiency on rock is much higher than that of methane, which can effectively sequester CO2 while achieving gas replacement and promote the goal of “carbon neutrality” [2-3]. The rock-breaking depth of SC-CO2 jet drilling technology is 1.65-7.85 times deeper than that of water jet, effectively improving drilling efficiency. However, the high-energy consumption and complex system of SC-CO2 jet limit its engineering application[4-5]. The key to reduce energy consumption and simplify the system is to improve the coal breaking efficiency and reduce the coal breaking pressure of SC-CO2 jet. It has been proven that self-excited oscillation pulsed SC-CO2 jets can generate higher pulse pressure than continuous jets, and improve coal-breaking efficiency [6]. Except of pulse pressure, pulse frequency is also one of the key factors affecting the coal breaking efficiency of self-excited oscillation SC-CO2 jet [7].
Studies on thin coals, coals on mining surface, and coal samples with different sizes found the inherent frequency is mostly from 0 to 2000 Hz [8⇓-10]. When impact frequency is consistent with the inherent frequency of coal or an integer multiple of the inherent frequency, SC-CO2 jet will resonate with coal, thus improving the breaking effect significantly. Impact frequency and the inherent frequency of rock have a significant effect on the vibrating period of the energy response of the rock. The impact from dynamic and static loads can expand the response range of the rock and the area of load action, increase the rock vibrating intensity, and promote rock breaking [11]. With the increase of static and dynamic loads and impact frequency, the damage to the rock increases. When the inherent frequency of the rock and the jet impact frequency are close to each other, the damage to the rock reaches the maximum [12]. The drilling speed can be increased by nearly 5 times compared to conventional rotary drill bit by using resonant drill bit for rock breaking [13]. Rock breaking by resonant drill bit is one of the important directions in the development of drilling technology.
The frequency and amplitude of the pulsed jet jointly damage rock, but the initial cracks mainly depend on the frequency [7]. With the increasing of pulse frequency, rock broken depth first increases and then decreases, so there is an optimal frequency range [14]. The structure of the self-excited oscillation nozzle can be changed to adjust the impact frequency of the self-excited oscillation pulsed jet to an optimal frequency for improving rock breaking efficiency [15-16]. The key to generating pulsed jets by self-excited oscillation nozzles is forming a stable shear layer and keeping the shear layer within a reasonable thickness and length range [17]. After generated, the eddy structure can fully develop during the motion and feedback within the shear layer, which forms a coherent structure and develops into a pulsed jet with a certain frequency. Changing the cavity-length-to-diameter ratio, collision wall angle, front and rear nozzle structures etc. affects the feedback and amplification laws of eddy structure in the shear layer inside the nozzle, which causes the change of impact frequency of jet [18-19]. Present studies on pulse frequency are based on the pulse characteristics of the pressure signal inside the nozzle. And the modulation of the frequency is based on the jet pulse frequency inside the nozzle [20⇓⇓-23]. However, when the jets impact rock, the jet frequency for forming a resonant interaction with the rock is the impact frequency acting on the rock surface. Due to changes of temperature and pressure in the environment, the two frequencies may not be the same. Our previous studies have shown that a continuous SC-CO2 jet has significant fluctuation in both pressure and velocity, and the pulse frequency is less than 1.3 kHz [24-25]. For SC-CO2 jets, changes of the jet structure and the environment cause the pulse characteristics of the jet to change continuously, and the frequency changes accordingly. Changing the nozzle structure can adjust the jet frequency inside the nozzle rather than the jet impact frequency required for resonant rock breaking.
To obtain the impact frequency of self-excited oscillation pulsed SC-CO2 jets for resonant coal breaking, large eddy simulation (LES) was conducted to analyze the formation and development process as well as the frequency variation of self-excited oscillation pulsed SC-CO2 jets inside the nozzle and in the free flow field, and analyze the variation law of the impact frequency. The proprietary device for testing self-excited oscillation pulsed SC-CO2 jet frequency was used to analyze the jet frequency variation under different conditions. Finally, compare the simulation and experimental results.
1. Numerical simulation
1.1. Physical model
The structure of the self-excited oscillation nozzle (Fig. 1 ) consists of an upstream nozzle (Laval nozzle), a Helmholtz oscillating cavity and a downstream nozzle. The structural parameters are shown in Table 1 .
Fig. 1. Nozzle structure of self-excited oscillation pulsed SC-CO2 jet. |
Table 1. Nozzle structure parameters of self-excited oscillation pulsed SC-CO2 jet |
| Parameter | Symbol | value |
|---|---|---|
| Inlet diameter of upstream nozzle | d | 7 mm |
| Throat diameter of upstream nozzle | d1 | 2 mm |
| Outlet diameter of upstream nozzle | d2 | 2.5 mm |
| Oscillating cavity diameter | D | 10 mm |
| Oscillating cavity length | L | 6 mm |
| Collision wall angle | θ | 120° |
| Length of downstream nozzle | L1 | 2.5 mm |
| Diameter of downstream nozzle | d3 | 3 mm |
1.2. Large eddy simulation
The formation and development of self-excited oscillation pulsed jets are closely related to the orderly generation of eddy structures and the formation of coherent structures. Compared with Reynolds-averaged simulation and direct numerical simulation, LES can accurately solve the turbulent motion above a certain scale, and thus capture the large-scale effects and the coherent structure that appear in the non-stationary equilibrium process. Therefore, LES was used to study the formation and development process of self-excited oscillation pulsed SC-CO2 jet, monitor the relationship between the jet velocity and time. To analyze the change of impact frequency, the fast Fourier transform (FFT) was used to transform the time-domain signal into the frequency- domain signal.
1.2.1. Governing equations
In LES, a filter function is used to divide the eddy rings according to the scale size. The equation of large-scale eddy motion is obtained by direct solution, and a subgrid-scale model is used to reflect the small-scale eddy motion. The continuity equation, momentum equation and energy equation of compressible ideal gas are obtained after filtering based on Navier-Stokes equation [6,26]. The WALE model was selected for the subgrid-scale model, with zero eddy viscosity in the laminar flow, which can correctly process the flow field simulation of near-wall laminar fluid [27-28]. It is necessary to construct the equations for physical properties of SC-CO2 in the numerical simulation. We have constructed theoretical computational models for the constant-pressure specific heat capacity, thermal conductivity and viscosity of SC-CO2 through partition fitting [29]. And based on user-defined functions (UDFs) and polynomial, the numerical models of SC-CO2 physical parameters were constructed through Fluent software, as shown in Eqs. (1)-(3).
The constant-pressure specific heat capacity is:
${{C}_{\text{p}}}=\left\{ \begin{align} & 184\ 1-0.000\ 1T\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( T\le 273\ \text{K} \right) \\ & 0.064\ 09{{\text{e}}^{-{{\left( \frac{T-318.9}{5.577} \right)}^{2}}}}+0.103{{\text{e}}^{-{{\left( \frac{T-324.5}{12.75} \right)}^{2}}}}+1.896{{\text{e}}^{-{{\left( \frac{T-329.1}{375.8} \right)}^{2}}}}+0.250\ 5{{\text{e}}^{-{{\left( \frac{T-334.4}{32.15} \right)}^{2}}}}\quad \quad \quad \left( 273\ \text{K}T\le 374\ \text{K} \right) \\ & 192\ 7-0.000\ 1{{T}^{^{^{^{^{^{{}}}}}}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( T>374\ \text{K} \right) \\ \end{align} \right.$
The coefficient of thermal conductivity is:
$k=0.845\ 8-0.003\ 649T+1.033\times {{10}^{-6}}{{T}^{2}}+1.513\times {{10}^{-8}}{{T}^{3}}-1.8\times {{10}^{-11}}{{T}^{4}}$
The viscosity coefficient is:
$\mu =3.293\ 34-0.028\ 831T+9.732\times {{10}^{-5}}{{T}^{2}}-1.479\ 05\times {{10}^{-7}}{{T}^{3}}+8.509\ 3\times {{10}^{-1}}{{T}^{4}}$
1.2.2. Mesh division and boundary conditions
The physical model was simplified to two-dimensional axisymmetric structure. Quadrilateral meshes were generated by ANSYS Meshing technology. The minimum mesh size was set to be 0.000 1 m, and 3 levels of refinement were applied to the wall to improve the mesh quality. The pressure was set to 45 MPa and temperature to 453 K at the inlet, while the pressure to 10 MPa and temperature to 353 K at the outlet. The wall was adiabatic and slip-free. The time step was 1×10−7 s, with 20 iterations in each time step. The total calculation time was 0.012 s. The boundary conditions are shown in Fig. 2 .
Fig. 2. Two-dimensional axisymmetric model after simplification. |
1.2.3. Numerical simulation programs
Numerical simulations were conducted to monitor the instantaneous velocity of the self-excited oscillation pulsed SC-CO2 jet at different locations inside the nozzle and in the free flow field. The locations of the monitoring points are shown in Table 2 [30]. The variation of jet velocity was monitored with time at different locations and different cavity lengths. The monitoring points were set at equal intervals of 2 mm from the nozzle outlet. The distance between monitoring points to nuzzle outlet was set as 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 mm. The cavity length was set as 3, 4, 5, 6, 7 mm.
Table 2. Monitoring points inside the nozzle and in the free flow field |
| Monitoring point | Position (x, y)/ (mm, mm) | Monitoring point | Position (x, y)/ (mm, mm) |
|---|---|---|---|
| 1 | (21.673, 4.95) | 5 | (29.500, 0) |
| 2 | (24.327, 4.95) | 6 | (31.500, 0) |
| 3 | (26.000, 3.25) | 7 | (35.500, 0) |
| 4 | (27.500, 0) | 8 | (43.500, 0) |
1.3. The impact frequency difference of self-excited oscillation pulsed SC-CO2 jet in nozzle and free flow field
The formation and development process of self-excited oscillation pulsed SC-CO2 jet is influenced by the structures of nozzle and flow field, which make the frequency of the jet different in the nozzle and free flow field (Fig. 3 ). Inside the self-excited oscillation nozzle, SC-CO2 is disturbed by the oscillating cavity to generate an eddy structure, which induces a pressure disturbance wave by the collision wall propagating upstream at acoustic velocity. When its phase coincides with the initial oscillation phase of the jet, the jet oscillation is superimposed and amplified to form wave A with frequency of 56 249.5 Hz [31]. Its frequency is the same inside the nozzle. At the nozzle outlet, the development of the jet is only related to the nozzle structure and the frequency is consistent with the disturbance frequency inside the nozzle. Since SC-CO2 is a compressible fluid, shock wave is induced after the jet is ejected by the nozzle under the influence of external environment and the pressure gradient between different fluids, and causes the jet velocity and pressure to pulsate (wave B) [6]. With the development of the jet, wave C is generated by the superposition of wave A and wave B, which makes the jet impact frequency in the free flow field change to 14 749.9 Hz [32]. Since the frequency of the jet impacting on rock surface resonates with the rock, the impact frequency in the free flow field should be optimized rather than the frequency inside the nozzle when studying resonant rock breaking.
Fig. 3. Impact frequency of self-excited oscillation pulsed SC-CO2 jets in nozzle and free flow field (cavity length is 6 mm). |
1.4. The variation of impact frequency of self-excited oscillation pulsed SC-CO2 jet at different points from the nozzle outlet
Fig. 4. The impact frequency of self-excited oscillation pulsed SC-CO2 jet varies with the distance from the nozzle outlets (cavity length is 6 mm). |
Fig. 5. Velocity cloud maps of self-excited oscillation pulsed SC-CO2 jets (with a 6-mm-long cavity). |
1.5. Influence of cavity length on the impact frequency of self-excited oscillation pulsed SC-CO2 jets
Fig. 6. Impact frequency of self-excited oscillation pulsed SC-CO2 jet with different cavity length. |
Fig. 7. Velocity cloud maps of jet with different cavity lengths. |
2. Experimental validation
2.1. Experimental system
To verify the impact frequency variation law of self- excited oscillation pulsed SC-CO2 jet from numerical simulation, frequency test experiment was carried out by using a SC-CO2 jet preparation system with high-frequency pressure sensor and high-frequency signal acquisition system. In the experiment, the impact pressure was collected and stored at real time, and the jet impact frequency was obtained after fast Fourier transform (FFT).
The SC-CO2 jet preparation system is composed of a CO2 supply system, a liquefaction system, a pressurization system, a temperature rising system and a central control system, including CO2 storage cylinders, cold bath boxes, air-cooled refrigeration compressors, storage tanks, high- pressure plunger pumps, hot bath boxes, heating buffer tanks and central control cabinet. The high-frequency pressure sensor and high-frequency signal acquisition system is composed of a high-frequency pressure sensor, a high-frequency signal acquisition card and data analysis software. The high-frequency pressure sensor is piezoelectric. The pressure range is 0-100 MPa; the inherent frequency of the sensor is not less than 200 kHz; the band width is 0.5-100.0 kHz; the impact resistance is 5000 g; and the working temperature is −40-125 °C. The maximum sampling rate of the high-frequency signal acquisition card is 500×103 times/s (500 ksps), and the sampling accuracy is 16 bit.
2.2. Experimental scheme
The experiments on the impact frequency of self-excited oscillation pulsed SC-CO2 jets were carried out using the self-excited oscillation nozzles with cavity lengths of 3, 4, 5, 6, 7 mm, respectively. The inlet pressure is 45 MPa and temperature is 453 K. The ambient pressure is 10 MPa, and temperature is 353 K. The data acquisition frequency is 200 kHz, and time is 5 s. The locations of the monitoring points are consistent with the numerical simulation.
2.3. Experimental results and analyses
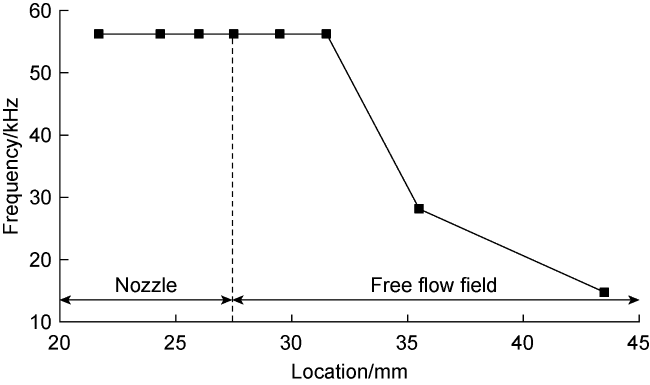
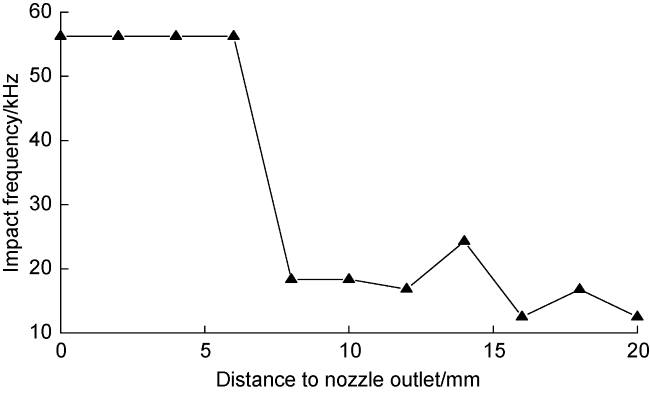
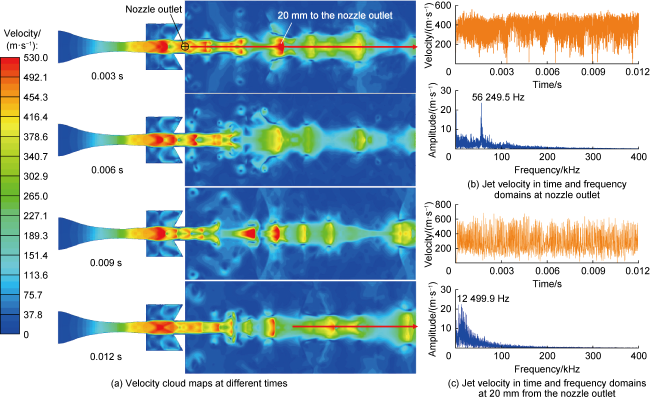
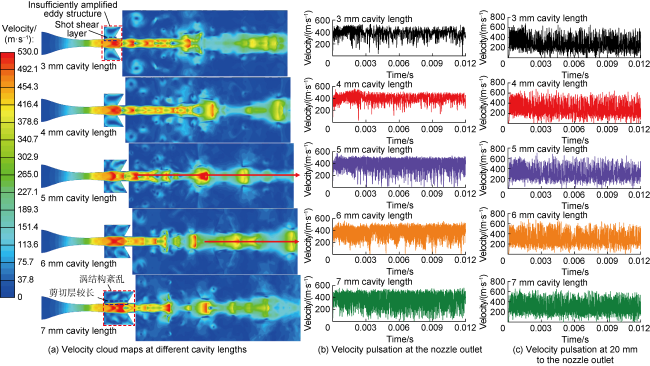
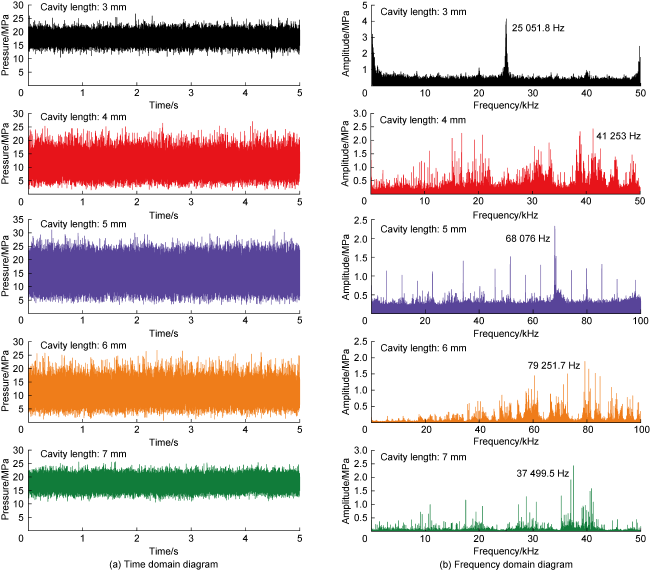
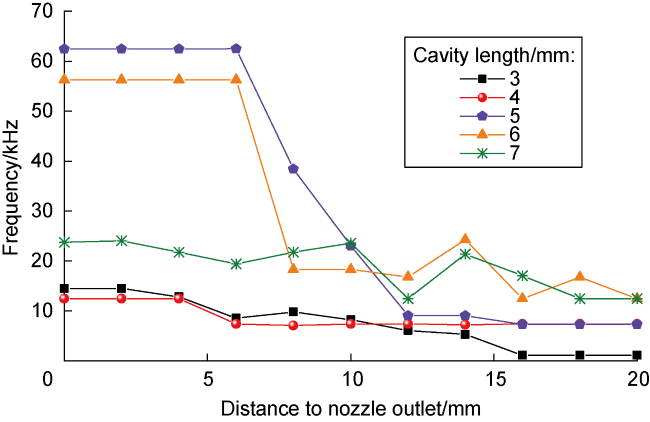
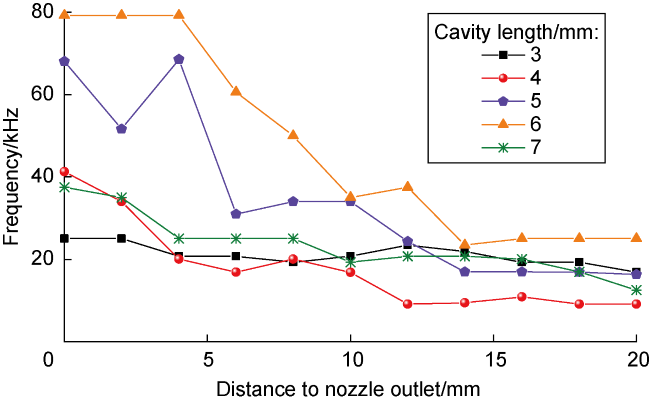
As shown in Fig. 8 and Fig. 9 , when the cavity length is 6 mm, the frequency of the self-excited oscillation pulsed SC-CO2 jet inside the nozzle is 79 251.7 Hz, and the amplitude is 1.89 MPa. After ejected from the nozzle, the jet impact frequency decreased to 25 004.4 Hz with the increase of the axial distance to nozzle outlet. When the cavity length is 3 mm, the jet impact frequency at the nozzle outlet is 25 051.8 Hz, and the amplitude is 4.14 MPa. After ejected, the impact frequency tends to oscillate and decrease to 16 898.2 Hz with the development of the jet. When the cavity length is 4, 5, 7 mm, there is a poor feedback effect of the eddy structure, which makes the pulsation of the initial shock wave at the nozzle outlet longer, so that the impact frequency of the self-excited oscillation pulsed SC-CO2 jet at the nozzle outlet reduced to 41 253, 68 076, 37 499.5 Hz, and the amplitude is 2.43, 2.32, 2.47 MPa, respectively. With the development of the jet, the impact frequency reduced to 9098.1, 16 290, 12 496.4 Hz, respectively. The self-excited oscillating pulsed SC-CO2 jet exhibits the rock breaking characteristics of high frequency and micro-amplitude under the nozzle structure. With the increase of the cavity length, the jet frequency at the nozzle outlet first increases and then decreases. With the increase of the distance to the nuzzle outlet, the jet frequency decreases as a whole. These conclusions are consistent with numerical simulations, which verify the variation law of the impact frequency of self-excited oscillation pulsed SC-CO2 jets. In field applications, the resonant frequency of coal under different excitation frequency conditions is not consistent, so the coal breaking effect can be enhanced by adjusting the length of the oscillating cavity to change the jet frequency. For example, if the inherent frequency of coal is 35 Hz [8], when using a self-excited oscillating nozzle with an oscillating cavity of 6 mm to break the coal at 0 mm from the nozzle, the impact frequency will be 2264.3 times the inherent frequency of the coal. To achieve the resonant coal-breaking effect, the length of the oscillating cavity can be adjusted to 5 mm, so that the impact frequency is 1945 times the inherent frequency of the coal.
Fig. 8. Pressure of self-excited oscillation pulsed SC-CO2 jets in time and frequency domains at the nozzle outlet with different cavity lengths. |
Fig. 9. Impact frequency of self-excited oscillation pulsed SC-CO2 jets with different cavity length conditions. |
3. Conclusions
After the self-excited oscillation pulsed SC-CO2 jet is induced in the nozzle, the pulse frequency does not remain constant with the development of the jet, but varies with the jet structure. In the jet axis, the pulse frequency decreases gradually with the development of the jet. To improve resonant coal breaking effect, we should change the impact frequency in the free flow field rather than the frequency inside the nozzle.
Inside the self-excited oscillation nozzle, SC-CO2 is disturbed to generate pulsed wave (wave A) whose frequency is related to the nozzle structure. A jet is formed after SC-CO2 is ejected out of the nozzle. Influenced by the compressibility of SC-CO2, the jet induces shock wave at the nozzle outlet, causing fluctuations (wave B) by the violent oscillation of jet velocity, pressure and temperature, etc. The pulse frequency is related to the structure of the jet flow field. Wave C is resulted from the superposition of waves A and B during the formation and development of the jet. The frequency of wave C is controlled by the structures of the nozzle and the jet flow filed. In this study, the jet frequency is 79 251.7 Hz at the nozzle outlet with a 6 mm cavity length, and it gradually decreased to 25 004.4 Hz in the free flow field, showing a decreasing trend.
With the increase of the cavity length, the frequency inside the nozzle tends to increase first and then decrease. After ejected from the nozzle, the impact frequency of the jet decreases in the axial direction. In field applications, the jet impact frequency can be optimized by adjusting the cavity length to achieve resonant coal breaking effects.
Nomenclature
Cp—constant-pressure specific heat capacity, J/(kg·K);
d—inlet diameter of upstream nozzle, mm;
d1—throat diameter of upstream nozzle, mm;
d2—outlet diameter of upstream nozzle, mm;
d3—diameter of downstream nozzle, mm;
D—diameter of oscillating cavity, mm;
k—thermal conductivity, W/(m·K);
L—length of oscillating cavity, mm;
L1—length of downstream nozzle, mm;
T—temperature, K;
x, y—rectangular coordinate system, mm;
μ—viscosity, Pa·s;
θ—angle of collision wall, (°).