Introduction
In recent years, carbon neutrality has received unprecedented attention worldwide [1]. Among the numerous technologies for carbon neutrality, Carbon Capture, Utilization, and Storage (CCUS) as well as Carbon Capture and Storage (CCS) are the foundational technologies for achieving carbon neutrality [2]. The CO2-water-rock systems are widely present in various industrial activities related to CCUS and CCS, including CO2 flooding and storage [3], supercritical CO2 fracturing and storage [4], saline aquifer CO2 storage [5], and Enhanced Gas Recovery (EGR) of gas reservoirs with water. China has significant potential for CO2 flooding and storage in gas reservoirs, CO2 flooding and storage in oil reservoirs, and CO2 storage in deep saline aquifer. The potential areas are mainly distributed in basins such as Songliao, Ordos, Bohai Bay, and Junggar [1-2].
The process of injecting CO2 into underground porous media involves at least the following fundamental issues: (1) Fluids flow in porous media. Subsurface rocks serve as porous media with a complex pore-throat structure, thus giving rise to fluids flow issues within the porous media. (2) Mass transfer (multicomponent transport). The ion composition of formation water is complex. In the interaction with CO2 and rocks, the concentration of ion components may undergo changes, giving rise to the issue of transporting multiple components. (3) Dissolution (heterogeneous chemical reaction). CO2 may undergo chemical dissolution reactions with some minerals in the rock, leading to changes in the pore-throat structure of the rock. This constitutes a heterogeneous chemical reaction issue. (4) Precipitate formation. Contact between CO2 and formation water may result in the oversaturation and crystallization of certain inorganic salts. In addition, the dissolution may induce the detachment of mineral particles from the main mineral body to generate new precipitates. (5) Precipitate migration. The generated precipitates may migrate along with the fluid under the influence of hydrodynamics, and phenomena such as precipitate deposition and re-suspension may also occur. Therefore, the CO2-water-rock systems involve interactions among CO2, formation water, and rock. In CO2-water-rock systems, dissolution and precipitation processes can lead to changes in rock porosity and permeability. Additionally, precipitate migration may significantly impact the fluid flow capacity of the rock, such as by blocking pores. The coupled effects of these physicochemical processes may result in drastic changes in the physical properties of the reservoir. Uncertainty and a lack of effective simulation and characterization methods for the microscale mechanisms of these processes can lead to inaccurate predictions of changes in macroscopic porosity and permeability parameters of the reservoir. Consequently, the evaluation of parameters such as storage capacity, injection and extraction capabilities, and storage integrity becomes unreliable [6]. This uncertainty impacts the reliability of formulating industrial injection and extraction schemes, as well as safety evaluations of CCUS and CCS.
Dissolution-precipitation-precipitate migration is a pore-scale behavior. Traditional core flow experiments often struggle to directly characterize the processes involved, such as changes in ion concentration, evolution of pore morphology, and tracking of precipitate migration. This limitation leads to a lack of clear understanding of the patterns of variation in reservoir physical parameters. Based on pore-scale microscopic flow simulation, it is possible to obtain a three-dimensional distribution of fluids, ions, pressure, etc., within the pore space. Additionally, explicit observation of the changes in the solid morphology of porous media with reactions can be achieved. This serves as a bridge connecting macroscopic and microscopic scales. Conducting pore-scale simulations of CO2-water-rock systems aids in determining the conditions and criteria for dissolution, precipitation, and precipitate migration. It quantifies their impact on the flow patterns, providing fundamental parameters for macroscopic numerical simulations.
This article provides a comprehensive review of the research status in three aspects related to the CO2-water- rock systems within the context of CCUS and CCS technologies. The three aspects include the complex mechanisms of CO2-water-rock interactions, microscopic simulations of porous media reaction transport (dissolution, precipitation and precipitate migration), and microscopic simulations of CO2-water-rock systems. The review discusses the strengths and weaknesses of domestic and international research, outlines the major issues and technological bottlenecks in the current research, and proposes future research directions.
1. Complex mechanisms of CO2-water-rock interactions
The CO2-water-rock system is a complex fluid flow system that couples processes such as flow, mass transfer, dissolution, precipitation, and precipitate migration, as illustrated in Fig. 1 . After CO2 is injected underground and comes into contact with formation water, it initially dissolves in water under the influence of gas phase pressure. The solubility of CO2 in water is directly proportional to pressure and inversely proportional to temperature and the salinity of formation water [7]. The solubility is primarily calculated using Henry constant, and there are also some commonly used empirical formulas [8]. After CO2 dissolves in water, it primarily exists in the form of free molecules, with only a fraction of CO2 combining with water to form H2CO3 (Eq. (1)). The dissolution reaction of CO2 in water is an equilibrium process, and in the absence of a catalyst, this reaction takes a long time to reach equilibrium [9]. This dissolution reaction releases H+, leading to a decrease in the pH of the solution, and the degree of decrease increases with the increasing solubility of CO2 [10]. At standard temperature and pressure, the pH value of CO2 saturated solution is 5.6. In acidic environments, the chemical properties of most minerals are unstable. H+ undergoes a series of chemical reactions with these minerals, leading to dissolution phenomena. This process may be accompanied by the release of new scaling ions (such as Ca2+, Mg2+, etc.). Simultaneously, when CO2 dissolves in water to form H2CO3, due to dissociation, further generation of HCO3- and CO32- occurs (Eq. (2) and Eq. (3)). These ions interact with scaling ions, resulting in precipitation phenomena. Therefore, the CO2-water-rock interaction leads to simultaneous processes of dissolution and precipitation.
CO2(g)+H2Ox $\rightleftharpoons$.H2CO3(aq)
H2CO3 $\rightleftharpoons$ H++HCO3-
HCO3- $\rightleftharpoons$ H++CO32-
Fig. 1 Schematic diagram illustrating the coupled transport of multiple physicochemical processes in the CO2-water- rock system. |
The interaction mechanisms in CO2-water-rock systems are studied primarily through static dissolution experiments and dynamic core displacement experiments [11]. Mineral composition analysis, scanning imaging, fluid composition analysis, and other methods are employed to monitor changes in mineral composition and pore-throat structure before, during, and after the reaction, and ultimately the variations in core porosity and permeability.
1.1. Mineral dissolution
Many rock minerals, such as calcite, dolomite and feldspar, and cements in the reservoirs have unstable chemical properties. When they come into contact with weakly acidic fluids formed by CO2 and formation water, dissolution occurs due to chemical reactions, as shown in Table 1 . The experimental results from some scholars indicate that CO2-water-rock reactions lead to an increase in rock porosity and permeability. In studies conducted by Na et al. [12], Cui et al. [13], Ding et al. [14], a series of dissolution experiments and core displacement experiments were carried out on carbonate rock cores under reservoir conditions. The results indicate that CO2, under the influence of formation water, caused significant mineral dissolution, leading to an increase in rock porosity and permeability. The phenomenon of increased porosity and permeability is not only observed in carbonate rock experiments but has also been found in sandstone experiments. Li et al. [15] immersed sandstone cores in CO2 water solution, resulting in strong dissolution effects on the cores. This was manifested by a significant decrease in calcite and dolomite content, an increase in the number of dissolution pores, and an enlargement of the original pore size. Ultimately, this led to an increase in both porosity and permeability. It is important to note that the reaction rates of different minerals can vary by several orders of magnitude [16-17]. Therefore, current laboratory experiments are limited by the time scale, and reactions with lower rates (taking hundreds to thousands of years) may not be observable in indoor experiments. This limitation hinders the assessment of the impact of CO2 on reservoir porosity and permeability on geological time scales.
Table 1 Chemical reaction between CO2 water solution and certain minerals |
| Mineral type | Mineral names | Chemical formula | The chemical reactions with CO2 water solution |
|---|---|---|---|
| Carbonate | Calcite | CaCO3 | CaCO3+CO2+H2O→Ca(HCO3)2 [18] |
| Dolomite | CaR(CO3)2 | CaR(CO3)2+2CO2+2H2O→Ca(HCO3)2+R(HCO3)2 [19] | |
| Magnesite, Siderite, Rhodochrosite | R(CO3)2 | R(CO3)2+CO2+H2O→R(HCO3)2 [19] | |
| Feldspar | Sodium Feldspar | NaAlSi3O8 | 2NaAlSi3O8+2CO2+3H2O→Al2Si2O5(OH)4+2Na++4SiO4+2HCO3－ [19], NaAlSi3O8+CO2+H2O→NaAlCO3(OH)2+3SiO4 [20] |
| Calcium Feldspar | CaAl2Si2O8 | CaAl2Si2O8+2CO2+3H2O→Al2Si2O5(OH)4+CaCO3 [18] | |
| Potassium Feldspar | KAlSi3O8 | 2KAlSi3O8+2CO2+3H2O→Al2Si2O5(OH)4+2K++4SiO4+2HCO3－ [21] | |
| Clay | Illite | K0.6Mg0.25Al2.3Si3.5O10(OH)2 | K0.6Mg0.25Al2.3Si3.5O10(OH)2+8H+→5H2O+0.6K++0.25Mg2++2.3Al3++ 3.5SiO2 [13] |
| Chlorite | A5Al2Si3O10(OH)8 | A5Al2Si3O10(OH)8+5CaCO3+5CO2→5CaA(CO3)2+Al2Si2O5(OH)4+ SiO2+2H2O [22] |
Note: R represents Mg/Fe/Mn, and A represents Mg/Fe. |
1.2. Mineral precipitation and migration
The dissolution of minerals may be accompanied by the formation of secondary minerals and the detachment of mineral particles induced by dissolution. These precipitates can migrate and block pores under hydrodynamic forces, leading to a reduction in rock permeability. The impact is often more significant on permeability than on porosity. Yu et al. [23] conducted displacement experiments under reservoir conditions (100 °C, 24 MPa) with CO2-saturated formation water. They observed that the porosity of the sandstone core remained essentially unchanged during the experiment, but the permeability continued to decrease. This was attributed to the migration of newly formed secondary minerals and clay particles released through the dissolution of carbonate cements to block pores. Mohamed et al. [24] conducted CO2 displacement experiments on sandstone, and the results indicated a 55% reduction in core permeability. They proposed two factors contributing to the decrease in core permeability: (1) Precipitates generated from CO2-water- rock reactions migrate and block pores. (2) Some cements react and dissolve, leading to the migration of the clay particles attached to the cements to block pores. Chen et al. [25] conducted displacement experiments with CO2-saturated water on sandstone with a permeability of 100×10-3 μm2 under conditions of 60 °C and 20 MPa. They found that the porosity of the core increased by 1.8%, and the permeability decreased by 5.1%. This was attributed to the particle migration induced by the dissolution of carbonate cements. Nunez et al. [26] studied the dissolution and precipitation characteristics in the near-wellbore and far-wellbore regions after CO2 injection by connecting two dolomite cores in series. They found that the porosity and permeability of the first core increased, while the porosity of the second core remained essentially unchanged. Secondary minerals formed in the first core migrated to the second core, causing pore blockage and ultimately leading to a reduction in permeability in the far-wellbore region. Wang et al. [27] found that after injecting CO2-saturated water into sandstone, the dissolution of carbonate minerals not only increased permeability but also induced particle migration leading to reduced permeability. When the salinity of the formation water was low, dissolution predominated, resulting in increased permeability. However, at higher formation water salinities, significant particle detachment and migration occurred, causing a decrease in permeability.
1.3. Evaporative crystallization
When dry supercritical CO2 is injected into the reservoirs with higher mineralization, it can lead to the evaporation of formation water to enter CO2. When the salt concentration in the formation water exceeds its solubility limit, crystallization is likely to occur, resulting in the precipitation of inorganic salts [28-29]. Specifically, there are four mechanisms as illustrated in Fig. 2 [30]: (1) CO2 injection into the reservoir results in two-phase flow, namely the supercritical CO2 phase and the saline reservoir water phase. After the supercritical CO2 displaces the reservoir water, residual water forms in the reservoir in the form of water films, water bridges, and other structures. Under the continuous flow of dry supercritical CO2, the residual water with salts begins to evaporate. With the evaporation of water, the relative permeability of CO2 increases, further promoting evaporation. (2) Due to the drying evaporation effect at the displacement front, a capillary pressure gradient is generated with the far-region high-water area. When this gradient exceeds the injection pressure gradient, reservoir water returns to the evaporation front, causing continuous evaporation [31]. (3) As water is evaporated into the supercritical CO2, the salt concentration in the residual water increases. This can lead to salt diffusion from the drying front towards the reservoir water side [32]. Once the salt concentration reaches its solubility limit due to evaporation, salts will precipitate out of the solution, forming precipitates. (4) The precipitated salt has a strong affinity for saline water, inducing the far-region saline water to move towards the evaporation front and evaporate, further increasing precipitation [33], which is similar to capillary suction. Therefore, when dry CO2 is injected into high-mineralization reservoirs, three typical regions are generally formed from the injection end to the reservoir end: a drying region with a significant number of precipitates, a two- phase flow region where CO2 displaces reservoir water, and a single-phase flow region of reservoir water.
Fig. 2 Mechanism of CO2 displacement-evaporation-precipitation (modified based on Reference [30]). |
A significant number of laboratory experiments and field practice have observed the phenomenon of inorganic salt precipitation induced by supercritical CO2 injection [33-34], as shown in Fig. 3 and Fig. 4 . In laboratory experiments, Berntsen et al. [35] injected supercritical CO2 into cylindrical sandstone samples saturated with formation water (40 °C, 10 MPa). Through scanning imaging and injection pressure monitoring, they observed salt precipitation and blockage in the rock matrix near the injection well. In field practice, in 2020, SaskPower discovered in the Aquistore CCS demonstration project that due to the high salinity of formation water in the reservoir (330 g/L), inorganic salt crystals were found around the CO2 injection well, leading to reduced injectivity. Analysis indicated that this salt precipitation was formed due to the continuous desiccation by CO2 [34].
2. Microscopic simulation of reaction transport in porous media
Compared to laboratory experiments, numerical simulations based on proportionate microscopic models offer advantages such as good repeatability, high flexibility, and low cost. The CO2-water-rock system is a typical coupled transport system of physicochemical processes, with dissolution, precipitation, and precipitate migration being the most significant features that distinguish this system from other fluid transport systems. The following sections elaborate on the progress in the microscopic simulation studies of these mechanisms.
2.1. Simulation of dissolution
For fluid transport systems involving dissolution processes, the equations to be solved include the fluid flow equation, the advection-diffusion equation for fluid components (mass transfer equation), the chemical reaction equation for solid-phase dissolution, and the geometric shape evolution equation describing solid dissolution. Scholars have proposed a series of methods to solve these equations (Table 2 ). The first category is traditional Computational Fluid Dynamics (CFD) discrete methods[36⇓⇓-39], such as Finite Volume (FV) and Finite Difference (FD) methods. The second category is particle methods applying the Lagrangian method to describe flow and mass transfer [40⇓-42], such as Smoothed Particle Hydrodynamics (SPH) and Moving Particle Semi-Implicit (MPS) methods. The third category involves hybrid computational methods [43-44], such as using FD to solve the flow equation and employing Random Walk (RW) to characterize solute transport [43]. Traditional CFD methods have a large computational cost, but in recent years, with the improvement of computer performance and the maturity of unstructured grids, this category of methods has gradually been employed to simulate the transport processes of reactive fluids. The mesh-free characteristics of particle methods make them well-suited for simulating turbulence, free surface flow, multiphase flow, etc. However, there are relatively few reports on the simulation of reactive flow and transport using particle methods. For hybrid computational methods, researchers often take advantage of mature software packages or certain methods with advantages in computational efficiency. They use different computational methods to solve different field equations. However, with the improvement of computer performance and the maturity of algorithms, an increasing trend is observed in using a single computational method to solve multiple physicochemical field problems. In recent years, a non-body-fitted grid simulation method called the Lattice Boltzmann Method (LBM) has been developed [45⇓⇓-48]. This method does not require the reconstruction or adjustment of the computational grid as the phases move in different regions. Compared with conventional CFD methods, LBM has advantages such as not being constrained by the assumption of fluid continuity, ease of considering microscopic mechanical characteristics, good adaptability to complex porous media, and simple parallelization. Therefore, an increasing number of researchers are using LBM to simulate flow and reaction processes in porous media.
Table 2 Microscopic simulation methods for dissolution reaction flow |
| Author | Calculation methods | Grid morphology | Interface update methods |
|---|---|---|---|
| Molins et al. [36] | CFD (FV) | Rectangular grid | LS |
| Xu et al. [37] | CFD (FD) | PF, LS | |
| Oltéan et al. [38] | CFD | Unstructured grid | ALE |
| Bracconi [39] | CFD (FV) | VOF | |
| Tartakovsky et al. [40] | SPH | SPH | |
| Xu et al. [41] | SPH | PF | |
| Ovaysi et al. [42] | MPS | Explicit representation | |
| Sallès et al. [43] | CFD(FD)+RW | Rectangular grid | Solid phase equilibrium critical value |
| Pereira-Nunes et al. [44] | CFD(FV)+PT | Rectangular grid | Solid phase equilibrium critical value |
| Szymczak and Ladd[45] | LBM | Solid phase equilibrium critical value | |
| Kang et al. [46-47] | LBM | VOP | |
| Chen et al. [48] | LBM | VOP |
In the simulation of reactive transport in porous media at the pore scale, the first challenge is to address the explicit representation of the spatial distribution of fluid and solid phases. If traditional CFD methods are employed, suitable techniques are needed to track or capture phase interfaces, such as the Level Set method (LS) [36], Phase Field method (PF) [37], Volume of Fluid method (VOF) [39], and Arbitrary Lagrangian-Eulerian method (ALE) [38]. When using these methods to simulate dissolution, it is necessary to continuously update the fluid-solid interface or reconstruct the grid according to the reaction to capture the evolution of the solid boundary over time and space. However, due to the complex shapes of solid boundaries within porous media, traditional numerical methods face challenges in handling evolving solid boundaries. LBM is a mesoscopic numerical method grounded in molecular kinetic theory. It efficiently handles solid boundaries of arbitrary shapes without the need to track, capture, or reconstruct complex phase interfaces. Its advantages in simulating complex flows within porous media are evident. Our research team has extended the traditional LBM to simulate fluid transport in shale nano-porous media [49⇓-51]. When employing LBM to simulate dissolution, several simple and efficient interface update methods have been developed, such as the solid-phase equilibrium critical value method and the Voxel Occupancy Probability (VOP) method [45⇓⇓-48]. In the simulation of chemical reaction transport, another issue to address is the impact of chemical reactions on the fluid component concentrations. When reactions occur between different components in the solution phase (homogeneous reactions), they can be handled by adding source-sink terms to the LBM equations. When reactions occur between solution components and solid surfaces (heterogeneous reactions), there are three representative methods for handling them in LBM: (1) Kang et al. [46-47] employed the thermodynamic boundary representation for heterogeneous reaction boundary proposed by He et al. [52] at the fluid-solid interface. (2) Patel et al. [53] proposed a pseudo-homogeneous method that accounts for the influence of heterogeneous reactions on fluid components by adding source-sink terms to the fluid nodes adjacent to the fluid-solid boundary. (3) The research team of Guo [54] proposed a local reaction boundary scheme for handling heterogeneous reactions. This scheme, built upon the bounce-back scheme, considers the effects of chemical reaction consumption and reversible reactions.
2.2. Simulation of precipitation
In the simulation of porous media, precipitation is the reverse process of dissolution, and the methods used in the simulation are similar. This includes boundary treatment methods and approaches to account for the influence of chemical reactions on fluid component concentrations. Therefore, the key to simulating precipitation lies in characterizing the precipitation process induced by different physical and chemical interactions. For the CO2-water-rock systems, the generation of precipitation mainly involves the precipitation of inorganic salts and the detachment of non-reactive minerals. Precipitation in porous media can significantly alter the flow paths of fluids [55], and it is crucial to accurately simulate the locations where precipitation occurs. Therefore, to achieve a reasonable simulation of precipitation, it is essential to conduct a thorough analysis of the precipitation mechanism based on the mechanisms of inorganic salt precipitation and non-reactive mineral detachment.
The precipitation of inorganic salts involves the formation of crystal nuclei and the growth of crystals after the solution becomes supersaturated. Nucleation can occur within the liquid, known as homogeneous nucleation, or at the interface between the liquid and solid, known as heterogeneous nucleation. Nucleation is the initial growth process that controls mineral precipitation. It is a probabilistic process, and crystals can nucleate anywhere with similar conditions such as surface properties, supersaturation and temperature [56]. The probabilistic nature of nucleation results in the generation of precipitates in different spatial locations within the porous media, affecting the flowing capacity of fluid. It is necessary to employ probabilistic methods or scale representation methods based on rational physical principles to characterize this phenomenon. Currently, in numerical simulations of inorganic salt precipitation, it is commonly assumed that nucleation occurs when the concentration reaches a certain threshold [48,57], without considering the probabilistic nature of the nucleation process. In recent years, some new dynamic models and formulas have been established to characterize the nucleation process based on the exponential nucleation rate equation in classical nucleation theory (CNT) (Eq. (4)). Some scholars have attempted to use CNT to predict the probabilistic nucleation behavior in precipitation simulations. Li et al. [58] coupled CNT into a continuous-scale simulator to characterize the precipitation of calcite, simulating the chemical changes in wellbore cement during CO2 storage processes. Prasianakis et al. [59] coupled a pore-scale reactive transport solver with CNT, demonstrating the impact of homogeneous and heterogeneous precipitation kinetics on the evolution of porous media. Hellevang et al. [60] studied the spatial distribution of secondary mineral growth on basalt columns through experiments and suggested the need to develop new probabilistic nucleation methods to characterize the stochastic nucleation process of inorganic salts. Fazeli et al. [61] developed a new probabilistic nucleation model based on CNT and coupled it with a pore-scale reactive transport solver. They simulated mineral nucleation and growth in porous media using single-component mineral reactions under different degrees of supersaturation, growth rates, and flow velocities. Masoudi et al. [62] further extended the model to simulate the formation of micron-scale inorganic salt crystals in CO2-rich phases and their impact on pore morphology and changes in permeability. Therefore, for the precipitation of inorganic salts, it is necessary to simulate the nucleation process of inorganic salts and characterize the differential growth between the nucleation phase and the original solid phase. Once the methods for characterizing the nucleation and growth of crystals are determined, similar to dissolution, it is necessary not only to update the fluid-solid geometric interface after inorganic salt precipitation but also to consider the influence of precipitation (crystal nucleation and growth) on the concentration of fluid ions by adding source-sink terms to the concentration diffusion equation.
$\ln \tau_{\mathrm{N}}=\frac{\beta V^{2} k_{\mathrm{B}}^{-3} \sigma^{3}}{T^{3}(\ln \Omega)^{2}}-\ln k_{\mathrm{N}}$
Detachment of non-reactive minerals can be classified into two types: Type I refers to the direct detachment of non-reactive minerals due to the dissolution of surrounding minerals. Type II refers to the shear detachment of weakly cemented surfaces under hydraulic forces due to mineral dissolution, as illustrated in Fig. 5. Type I can be determined using a calibration function. If, during a certain time step, non-reactive minerals are not connected to the main rock body, it is considered that non-reactive minerals have detached, forming precipitates. For instance, Liu et al. [63] employed the Hoshen- Kopelman algorithm [64] to assess the relationship between detached minerals and the main rock body, enabling the identification of mineral detachment caused by dissolution in reactive processes. For Type II, an initial step involves a global spatial search to identify potential weak cementation points. Subsequently, an analysis is conducted on the stress conditions of these weak cementation points in the minerals. When the flow velocity reaches a certain value (critical velocity), if the torque of the drag force exerted by the fluid on the mineral particles (Fd) is sufficient to overcome the combined torque of the contact force (Fc1), cementation force (Fc2), and adsorption force (Fa), it is considered that mineral detachment occurs, forming precipitates, as illustrated in Fig. 5. Therefore, initially, based on the reaction rates of different minerals, a mineral dissolution simulation method is employed for simulation calculations. At each calculation time step, the generation of Type I or Type II precipitation is determined. If present, subsequent simulations are conducted for the transport, deposition, and re-activation (re-suspension) of the precipitate. As of now, there are no reported simulations specifically addressing Type II precipitation.
Fig. 5 Diagram illustrating the detachment of non-reactive minerals resulting in precipitation after the dissolution of reactive minerals. |
2.3. Simulation of precipitate migration
The CO2-water-rock systems may lead to precipitates, and under the influence of hydraulic forces, the precipitates can migrate and potentially clog pore throats, significantly reducing the permeability of the porous media. The migration of precipitates is fundamentally similar to the transport of particles in solution, and there are numerous reports in the literature regarding simulation methods for particle transport. These methods are generally classified into Euler-Euler method and Euler-Lagrange method [65]. The Euler-Euler method treats both the fluid and particles as continuous phases, while the Euler-Lagrange method considers the fluid as a continuous phase and the particles as a discrete phase, providing a detailed representation of their trajectories by tracking the movement of individual particles discretely. Among the Euler-Lagrange methods, the Discrete Element Method (DEM) is widely employed in studying particle flows, considering the interaction forces between particles and fluids, and demonstrating clear advantages [66⇓-68]. The fundamental idea of DEM is to consider discrete particles as individual entities, where different particles come into contact through corners, faces, or edges. The motion of particles, including translation and rotation, is governed by Newton second law. The contact forces between particles are calculated using appropriate contact models [69]. The linear contact model is the most basic contact model, where the contact forces and torques between particles are simplified to be proportional to the deformation for calculation, significantly simplifying the simulation of contact forces and torque variations. For rock particle systems, commonly used contact models include the linear parallel bond model, planar joint model, and soft bond model [65]. These models simplify the complex nonlinear contact processes between particles, reducing computational complexity and making them suitable for specific engineering problems.
Currently, most DEM simulations are based on spherical particles, while the precipitates generated in the CO2-water-rock systems are typically non-spherical particles. Compared with spherical particles, the challenges in DEM simulations of non-spherical particles are primarily reflected in the following two aspects [70]: (1) The contact determination between non-spherical particles is more complex, and when the particle shape changes, the collision contact algorithm also changes accordingly. (2) The force analysis between non-spherical particles is difficult to achieve high accuracy. The current methods for describing the shape of non-spherical particles can be categorized into multi-body combination method and precise geometric shape description method[71]. Multi-body combination methods use basic units such as spheres or other shapes to construct complex particle shapes. The advantage of this method lies in the relatively simple contact detection between constructed units, requiring a balance between the geometric shape description accuracy and simulation computational efficiency. Precise geometric shape description methods strictly rely on the geometric shape of particles for collision detection. Contact detection is more complex in this method, but its advantage lies in high accuracy in particle contact detection. The computational workload is related to the number of particles and the complexity of the contact detection algorithm, making it suitable for simulations of non-spherical particle systems with size variations.
Similar to dissolution or precipitation, DEM can be coupled with traditional CFD, particle methods (such as SPH), LBM, and other methods to simulate particle flow[72], as shown in Fig. 6. Considering the advantages of LBM in simulating the flow in porous media, here we only provide a review of the current research status of LBM-DEM fluid-solid coupling simulations. In the early stages of LBM research [73], to establish a fluid-particle interaction system, when the particle boundaries intersected with the fluid grid, the numerical boundaries of solid particles were considered to be at the midpoint of the LBM lattice. However, this method cannot accurately couple and calculate the fluid-solid interaction forces, potentially leading to oscillations in the numerical drag force when particles move rapidly. Noble et al. [74] proposed the Immersed Moving Boundary (IMB) method, suggesting that the Lagrangian points on solid particles are located at the intersection of particle boundaries and fluid grid. The method advocates using the solid volume fraction, which is the area fraction of the fluid grid cell covered by the particle, to calculate the fluid-solid interaction forces. In recent years, an increasingly popular method for addressing complex moving boundary problems is the Immersed Boundary Method (IBM), originally proposed by Peskin [75] for simulating the flow of blood cells. In this approach, a particle is represented by a set of independent points, and the positions of Lagrangian points can be straightforwardly determined based on the position and orientation of particles. The total force and torque on the particle are calculated by summing the changes in momentum for all Lagrangian points on the particle. This method was initially applied to LBM-DEM coupled simulations of spherical particles and has since been extended to the simulation of flow involving two-dimensional non-spherical particles [76] and three-dimensional non-spherical particles [77].
Fig. 6 DEM coupling method for particle flow (modified based on Reference [72]). |
3. Microscopic simulation of the CO2-water-rock system
Due to the significant advantages of LBM in simulating multiple physicochemical reaction transport system, in recent years, researchers have started to explore the use of LBM to simulate CO2-water-rock systems, resulting in important progress and insights.
For the simulation of dissolution, dissolution reaction kinetics models are commonly used to predict dissolution rates. The pore-scale mineral dissolution/precipitation rates can be described using Transition State Theory (TST). The reaction rates of all minerals can be expressed in the following general form [78]:
${{R}_{m}}=-{{k}_{m}}{{\left( 1-\frac{{{Q}_{\text{s}}}}{{{K}_{\text{eq}}}} \right)}^{n}}$
According to Eq. (5), the dissolution/precipitation rate of calcite mineral in a CO2 acidic environment at room temperature (25 °C) can be expressed as:
$R=\left( {{k}_{1}}{{\alpha }_{{{\text{H}}^{+}}}}+{{k}_{2}}{{\alpha }_{{{\text{H}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}}}+{{k}_{3}} \right)\left( 1-\frac{{{\alpha }_{\text{C}{{\text{a}}^{2+}}}}{{\alpha }_{\text{C}{{\text{O}}_{\text{3}}}^{\text{2}-}}}}{{{K}_{\text{eq},\text{CaC}{{\text{O}}_{\text{3}}}}}} \right)$
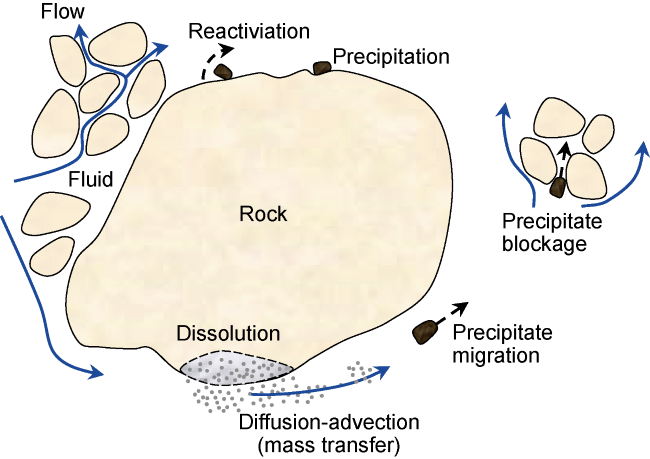
In addition to the above calculation methods, some researchers directly utilize the geochemical simulator PhreeqcRM to obtain reaction rates. Whether directly employing LBM simulation or combining LBM with other CFD discretization methods (e.g. FV, FE, and FD), along with digital core technology and parallel processing techniques, it is feasible to achieve three-dimensional pore-throat simulation of CO2-water-rock system dissolution reactions at the core scale. This approach enables the quantitative assessment of changes in pore throat, porosity, and permeability induced by dissolution. In static dissolution simulations, Gao et al. [81] considered the calcite cement in sandstone as reactive, while other minerals were considered non-reactive. They used LBM to simulate the static dissolution process of CO2-water-rock. 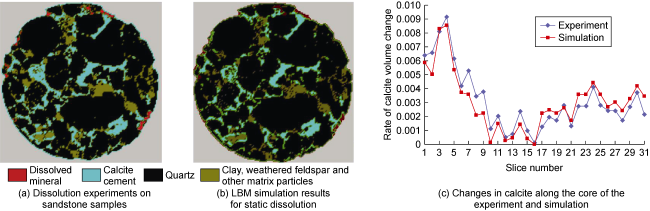The results were compared with dissolution experiments conducted by previous researchers [82], as shown in Fig. 7. The model simulated the reaction process between carbonic acid solution and calcite for a duration of 1 440 days, until reaching the equilibrium state of the reaction. Due to the dissolution of calcite, the porosity of the rock core increased from 1.1% to 10.7%. They found that the spatial distribution of calcite in the rock core is crucial. Due to the fact that some calcite is not directly in contact with the acidic fluid, more than one-third of the calcite remained undissolved. In dynamic dissolution simulations, using the pseudo-homogeneous reaction boundary established by Patel et al. [53], Fazeli et al. [83] simulated the evolution of fracture dissolution in carbonate rock samples after the injection of CO2-saturated brine. The results showed that non-reactive minerals present along the flow path can limit the increase in permeability. The commonly used cubic relationship between porosity and permeability in single-mineral porous media fails in multi-mineral porous media. To simulate the CO2-water-rock reactions at the core scale, An et al. [84] coupled LBM with the geochemical simulator PhreeqcRM. They evaluated the evolution of porosity and permeability over time under different injection rates, pressures, and temperatures. With increasing flow rates, the dissolution in the rock became more uniform, and they suggested that the permeability increase at high injection rates was larger than that at low injection rates. Xie et al. [85] employed LBM for fluid flow and component transport and utilized the VOP method to handle the boundary evolution caused by reactions. They simulated the dissolution of calcium carbonate during the CO2 sequestration process, elucidating that the effect of pressure difference on calcium carbonate dissolution weakened with increasing temperature. They plotted a diagram of the calcium carbonate dissolution pattern based on the relationship between temperature and pressure, suggesting that injecting CO2 at high temperatures and high injection rates facilitates its dissolution and sequestration. Ju et al. [86] employed a local reaction boundary format that considers the impact of chemical reaction consumption and reaction reversibility. They simulated the advection-mixing process in the underground saline aquifer for CO2 sequestration, and analyzed the influence of fluid-rock dissolution reactions and H2S impurity components on system stability.
Fig. 7 Static dissolution experiments of CO2-water-rock system and corresponding LBM simulations [81]. |
In the simulation of chemical reactions involving mineral dissolution, the numerical uncertainty of important geochemical reaction-related parameters of minerals (equilibrium constants, reaction rate constants, etc.) is a primary factor limiting the accuracy of numerical simulations. For example, Gray et al. [87] pointed out that when using LBM to simulate CO2-saturated solution, it is necessary to consider the nonlinear dynamic model of dissolution reactions (n1 in Eq. (5)) and a multi-component diffusion coefficient model. However, even with these considerations, when comparing the simulation results with the carbonate rock experiments conducted by Menke et al. [88], it was found that the simulated results were several times faster (Fig. 8 ). This discrepancy was attributed to the uncertainty in some key parameters of the model. In addition, the experimental dissolution rate showed a square root relationship with time, while the simulated dissolution rate was approximately linearly correlated with time. This discrepancy was attributed to the possibility that the CT scan precision was not high enough to capture the ion diffusion in some smaller pores, leading to a higher dissolution rate in the simulation. In pore-scale reaction simulations, certain slow reaction processes are often considered non-reactive, potentially underestimating the reaction rates of some minerals. In long-term, macroscopic simulations, some rapidly reacting minerals (e.g. CaCO3) are often treated as equilibrium phases, which may overestimate the actual reaction rates in porous media.
Fig. 8 CO2-water-rock dynamic displacement-dissolution experiment and corresponding LBM simulation [87]. |
In the simulation of precipitate generation and migration in the CO2-water-rock systems, in addition to the aforementioned studies on inorganic salt crystallization precipitation, other researchers have also conducted simulations of precipitation in the CO2-water-rock systems. Jiang et al. [57] used the color-gradient LBM model to solve the two-phase flow equations and FV method to solve the component transport equations. Considering that inorganic salt precipitation occurs when the concentration reaches a certain threshold, the simulation revealed that the changes in pore structure caused by precipitation markedly reduced the absolute permeability of the porous media. Additionally, the impact on the relative permeability of the non-wetting phase was greater than that on the wetting phase. Liu et al. [63] used the LBM to solve the flow equations and FV method to solve the component transport equations. Through a simplified approach based on Stokes law, they coupled the migration of particles released by dissolution to the LBM reactive transport model, exploring the transport process of solid precipitates, as shown in Fig. 9. By comparing with the results of dynamic core displacement experiments monitored by online X-ray Computed Tomography (Micro-CT), it was found that the simulation results could well match the changes in porosity along the displacement direction at different time steps. Through extensive simulations of carbonate rock porous media, a power-law relationship between permeability and porosity was discovered. The simulations also explored the impact of the migration of the solid particles released by dissolution on permeability. Parvan et al. conducted a similar simulation study [89], but in the simulation, they assumed that all solid-fluid surfaces could react, neglecting the chemical heterogeneity of rock surfaces and the effective reactive contact areas. In addition to the uncertainties in studies focusing on the precipitation of single mineral, some scholars have pointed out that it is challenging to determine the types of secondary minerals formed after dissolution reactions, quantify their generation, and set up enough kinetic parameters for these reactions. This difficulty in simulating some secondary minerals could have a significant impact on the results of chemical reaction simulations [90].
Fig. 9 CO2-water-rock dynamic displacement precipitation-migration experiment and corresponding LBM simulation [63]. |
4. Existing issues and recommendations
(1) The decoupling of complex mechanisms (such as dissolution, precipitation, and precipitate migration) in the CO2-water-rock systems: The injection of CO2 into the reservoir disrupts the physical and chemical balance between formation water and rock, leading to phenomena such as dissolution, precipitation, and precipitate migration. The combined effects of these processes can result in complex changes in reservoir permeability, including increases, decreases, and fluctuations. Dissolution-Precipitation-Precipitate migration is a pore-scale behavior, and traditional core flow experiments often struggle to visually characterize its processes (such as changes in ion concentration, evolution of pore morphology, tracking of precipitate migration, etc.). This leads to a lack of clarity in understanding the variation patterns of reservoir rock properties and difficulties in prediction. Therefore, further in-depth analysis of the coupled flow mechanisms of dissolution, precipitation, and precipitate migration in the CO2-water-rock systems is needed. Specifically, various complex mechanisms (dissolution, precipitation, and precipitate migration) can be decoupled through different experimental equipment and visualization methods to systematically study the characteristics and patterns of each mechanism. For example, static dissolution experiments can be employed to analyze the differential dissolution patterns of multiple minerals. Etching glass experiments can be utilized to capture the precipitation (crystallization) and precipitate migration patterns under formation water supersaturation conditions. Online core displacement experiments can be conducted to analyze the dissolution, precipitation, and precipitate migration patterns under displacement conditions.
(2) Methods for measuring reaction coefficients and micro-characterization of differential reactions in multi- mineral systems: In general, compared with traditional CFD or Lagrangian particle methods, LBM has clear advantages in simulating complex flow within porous media. These advantages include ease of handling complex boundaries, capturing phase interfaces, and facilitating parallel computing. For reaction-transport flows, the representation of homogeneous reactions in the solution and heterogeneous reactions at the fluid-solid interface can be achieved by adding source-sink terms to the LBM equations and incorporating appropriate boundary update schemes. This approach has been widely applied in various physicochemical reaction flows. In the CO2-water- rock systems, reactions may occur between CO2 aqueous solution and different formation water components as well as different minerals, and the reaction rates are different. It is essential to conduct experiments for calibrating reaction rates between CO2 aqueous solution and different ions or mineral components under varying temperature and pressure conditions. This will enhance the accuracy of experimental testing and reduce the numerical uncertainty associated with key mineral geochemical reaction parameters such as equilibrium constants and reaction rate constants. Ultimately, this will improve the reliability of numerical predictions for the flow equations governing component exchange.
(3) The formation mechanism and characterization of precipitates under the actions of crystal nucleation and mineral detachment: The location, size, and migration capacity of precipitates directly affect the permeability of porous media. Therefore, the characterization of precipitate generation is crucial for the success of micro-scale simulation of CO2-water-rock systems. The generation of precipitates includes the precipitation of inorganic salts and the detachment of non-reactive minerals. The crystallization nucleation of inorganic salts is controlled by the probability nucleation theory, and the crystal growth also follows certain rules. However, current research reports on the characterization of crystalline precipitation are overly simplified, treating nucleation and crystal growth as a random process. Induced by the dissolution of surrounding minerals and the weakening of cementation at vulnerable sites, the detachment of non-reactive minerals from the main solid phase is another important mechanism for the generation of precipitates. However, there is currently no research on the relevant mechanisms and characterization methods for this process. Therefore, it is necessary to predict the formation process of inorganic salts based on crystal nucleation theory, propose methods to discern the detachment of non-reactive minerals, and thus establish reliable characterization methods for precipitate generation.
(4) Methods for simulating the interactions between fluid and precipitates of irregular shape, multi-type, varying quantity, and changing shape: The migration of precipitates (particles) in porous media is a key factor influencing the permeability of the CO2-water-rock systems. DEM is the most commonly used approach for simulating particle flow in porous media. Combined with the IBM, it can simulate the particle-fluid interaction in the LBM system. The simulation of particle migration in CO2-water-rock systems has three distinctive aspects: The formation of precipitation is diverse (secondary minerals, detachment of mineral particles). The shape of the precipitate is generally irregular. The generated precipitates may disappear (dissolve) during the migration process, meaning that the quantity and size of the precipitates may change during migration. Therefore, it is necessary to establish a method for simulating the interactions between fluid and precipitates of irregular shape, multi- type, varying quantity, and changing shape according to different formation mechanisms and geometric characteristics of precipitates.
(5) The coupled seepage mechanism of multiple physicochemical processes in the CO2-water-rock systems: In recent years, some researchers have used LBM to simulate reactive flow in the CO2-water-rock systems. However, the established simulation methods mainly focus on individual or a few physicochemical processes. The injection of CO2 into reservoirs involves multiphase (gas/water/oil), multicomponent (CO2 aqueous solution, H+, HCO3-, CO32-, and OH−, etc.), and heterogeneous/homogeneous chemical reaction processes. Achieving a fully coupled simulation for these complex processes poses a challenging problem. The various physicochemical processes in the CO2-water-rock system are coupled and influenced each other. For example, the dissolution of minerals may induce the detachment of surrounding minerals, leading to the precipitation. After the migration of the precipitates, the exposed fresh mineral surfaces may undergo new dissolution upon contact with CO2. Based on the literature review, current research on this issue primarily focuses on one or a few physicochemical processes. Failure to effectively coordinate the coupling relationships among different mechanisms may result in significant discrepancies between simulation results and laboratory experiment results. Therefore, there is a need for a coordinated connection between the simulation boundary conditions of various physicochemical processes and the coordination of coupling relationships between these mechanisms. This is essential for quantitatively evaluating the impact of dissolution, precipitation, and precipitate migration on porosity and permeability.
5. Conclusions
After the injection of CO2 underground, it disrupts the physical and chemical equilibrium between the formation water and the rock, leading to special phenomena such as dissolution, precipitation, and precipitate migration. These processes can have a significant impact on the injectivity of CO2, the sealing effectiveness of the caprock, and the overall reliability of CO2 geological storage. Currently, based on macroscopic high-temperature and high- pressure static experiments, core permeability experiments, and other methods, it is challenging to fundamentally understand the coupled dissolution-precipitation-precipitate migration mechanisms in the CO2-water-rock system. This limitation hinders the effective prediction of the complex changes in macroscopic porosity and permeability parameters. Conducting research on the coupled seepage mechanisms and microscopic simulations of these specific physicochemical processes is an effective approach to quantify the changes in the pore-throat structure of porous media and predict the complex variations in permeability resulting from physicochemical reactions.
The study of the coupled seepage mechanisms and microscopic simulation of dissolution-precipitation-precipitate migration in CO2-water-rock systems still faces several key scientific issues. For instance, considering the differential dissolution reactions between CO2 and different minerals in formation water, it is necessary to establish a simulation method for heterogeneous mineral dissolution. For different types of precipitation mechanisms (such as secondary minerals generated by chemical reactions and mineral particle detachment induced by dissolution), it is necessary to establish appropriate methods for characterizing the formation of precipitates. It is necessary to establish a method for simulating the interactions between fluid and precipitates of irregular shape, multi-type, varying quantity, and changing shape. It is necessary to connect the simulation boundary conditions for various physicochemical processes and coordinate the coupling relationships between different mechanisms. If these issues are appropriately addressed, it will be possible to achieve visual simulations of dissolution-precipitation-precipitate migration in porous media for carbon sequestration.
In future research, it is crucial to decouple dissolution- precipitation-precipitate migration by means of static dissolution experiments, etching glass experiments, and online core displacement experiments, combined with laboratory visualization experiments and micro-scale simulations, so as to provide validation data for the microscale simulation methods of each process. For instance, when LBM and DEM are used as fundamental simulation techniques to handle the processes of flow, mass transfer, and precipitate migration, they are coupled with the simulation methods based on the dissolution kinetics for heterogeneous mineral dissolution and the precipitation simulation methods based on crystal nucleation theory and mineral detachment discrimination methods to form a microscale simulation technology for coupled flow of dissolution, precipitation, and precipitate migration. This approach allows for the quantitative prediction of seepage-related parameters in the CO2-water-rock system. It provides a theoretical basis and technical support for the safe and efficient implementation of CCUS and CCS industrial activities.
Nomenclature
Fa—adsorption force between fluid and mineral particles, N;
Fc1—contact force between fluid and mineral particles, N;
Fc2—cementation force between fluid and mineral particles, N;
Fd—drag force exerted by fluid on mineral particles, N;
kB—Boltzmann constant, with a value of 1.38×10-23 J/K;
km—reaction rate constant for the m-th mineral, mol/(m2•s);
kN—nucleation rate constant, 1/(m2•s);
Keq—reaction equilibrium constant, dimensionless;
Keq,CaCO3—reaction equilibrium constant for CaCO3, dimensionless;
n—reaction order;
Qs—ionic activity product, dimensionless;
R—dissolution/precipitation rate of calcite mineral in CO2 acidic environment, mol/(m2 s);
Rm—reaction rate of the m-th mineral, mol/(m2•s);
T—absolute temperature, K;
V—volume of the nucleation phase, m3;
${{\alpha }_{{{\text{H}}^{+}}}}$, ${{\alpha }_{{{\text{H}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}}}$, ${{\alpha }_{\text{C}{{\text{a}}^{2+}}}}$,${{\alpha }_{\text{C}{{\text{O}}_{3}}^{2-}}}$—activity of H+, H2CO3, Ca2+, CO32-, dimensionless;
β—geometric factor, dimensionless;
σ—interface free energy between the nucleation phase and the substrate, J/m2;
τN—induction time, (m2·s);
Ω—supersaturation, %.