During logging operations in the same well in different stages, variations in cable tension occur due to factors such as the lifting speed of the logging tool, the position movement of the derrick pulley, the weight of the logging tool, the friction between the cable and tool string with the wellbore, and drilling mud specific gravity, etc. These variations cause depth discrepancies between different well logs. Whether they are direct or indirect factors, depth errors are inevitable. Consequently, logging companies around the world set the depth delay of the sample points on the well logs recorded in the second stage (ϕ_CNL, ρ, GR₂) as the same as preset values ^[25]. They use GR₁ as a depth reference, and match GR₂ with GR₁ to make preliminary depth matching of the well logs at different stages (Fig. 1).

During the same stage of logging operations, depth discrepancy may arise between different well logs if logging tools are stuck or subjected to runout when lifted up, resulting in the stretch or compression of the well logs. In addition, depth delay of sample points, the friction between logging tools and the wellbore and the adhesion effect of drilling mud may cause depth discrepancy, too. Although the depth errors between well logs measured in the same stage tend to be smaller than those between different stages, they cannot be neglected when downhole conditions are poor. As shown in Fig. 1, both the depths of Δt, SP and GR₁ recorded in the first stage, and the depths of ϕ_CNL, ρ, etc., recorded in the second stage need to be corrected by referring to GR₁.

Reinforcement learning (RL) is a significant branch of machine learning, where the problems that RL aims to solve are typically abstracted into the interactions between the agent and its environment. In this paper, the decision-making subject that learns and implements depth matching of well logs is referred as the agent, and any external entities interacting with the agent are termed the environment, which includes input well logs and historical matching records. The matching status of the current well log observed by the agent in the environment is called a state, and a set of operations (translating, scaling or stopping) taken by the agent to act on the environment to change the matching status of the well log is called an action. RL attempts to solve a Markov decision-making optimization problem based on the interaction between the agent and the environment ^[26]. In a single-agent system for depth matching, the system can process inputs from two well logs, generally GR₁ and GR₂ (Fig. 2a). To achieve simultaneous and automatic depth matching between target well logs (e.g. GR₂, ϕ_CNL, ρ, Δt, etc.) and the reference well log (GR₁), this paper defines the execution subject for depth matching of each pair of well logs as an agent. This approach expands the single-agent reinforcement learning system into a multi-agent one (MARL, Fig. 2b).

Similar to the single-agent reinforcement learning process, the multi-well log depth matching process in a multi-agent system is also a Markov decision process (MDP), as shown in Fig. 2b. The difference is that when multiple agents interact with the same environment, they not only cooperate to observe the environment to update the status and obtain the maximum cumulative reward but also independently complete the depth matching between the corresponding target well log and the reference well log. The interaction process between agents is shown in Fig. 2b. At time t, the ith agent observes the current state s_{t,i} of the environment and selects an action a_{t,i} under a specific strategy {\pi }_{t,i} to act on the environment. Then, all agents execute a joint action A_t=\left\{a_{t,1},a_{t,2},...,a_{t,N}\right\} based on a joint strategy P_t= \left\{{\pi }_{t,1},{\pi }_{t,2},\cdots ,{\pi }_{t,N}\right\}^[27]. The environment responds to this action, leading to a new state s_{t+1}, and each agent receives a reward r_{t+1,i}. This process is repeated at the next time step t+1, generating a series of rewards R_{t+1}= \left\{r_{t+1,1},r_{t+1,2},\cdots ,r_{t+1,N}\right\} and new states S_t=\left\{s_{t,1}^{},s_{t,2}^{},...,s_{t,N}^{}\right\}, thus creating a Markov decision sequence \left\{S_0,A_0,R_1,S_1,\right. \left.A_1,...,S_t,A_t,R_{t+1},S_{t+1}\right\}. Through this iterative cycle, the agents learn an optimal strategy to perform actions and obtain maximize rewards, ultimately achieving automatic matching of multiple well logs.

In 2001, Aach et al. ^[12] introduced a dynamic time warping (DTW) method for aligning different time series of biological gene expressions to observe and analyze the changes in gene activity over time. Subsequently, Wang et al. ^[11] applied this method for automatic depth matching between the sequences (X={x₁, x₂,…, x_n}) on GR₁ and the sequences (Y={y₁, y₂,…, y_n}) on GR₂. By constructing a cost matrix ( C_{m\times n}=(C_{i,j})) from the Euclidean distances between corresponding points on the well logs, the similarity and matching effect between the sequences are maximized when the cumulative distance between corresponding points in the two sequences is minimized, as shown in Eq. (1). However, when processing well logs with large-scale sampling points, DTW will increase the computational complexity and make the matching results unstable ^[1]. In response to the above problems, Bittar et al. ^[24] introduced the DQN method ^[26] for automatic depth matching between GR logs. This method can quickly and continuously self-learn to improve the control optimization process in the depth matching task. However, DQN faces a significant challenge: when estimating the expected return (Q-value function, as shown in Eq. (2)) for an action ( a_{t,i}) taken by an agent in the current state ( s_{t,i}), the value function update tends to overestimate the Q-values, leading to instability in the training process and ultimately resulting in suboptimal strategy ^[28]. To address this issue, our study proposes a multi-agent reinforcement learning model based on DDQN, which mitigates overestimation through a dual-network (evaluation and target networks) evaluation mechanism. The DDQN framework for depth matching of multi-well logs (Fig. 3) includes a dual sliding window, a dual-network evaluation mechanism and an experience replay pool.

The depth matching task is to convolve the feature sequences on multiple well logs through multiple dual- channel one-dimensional CNN (dual sliding windows) and input them into the DDQN network. One agent can input the feature sequences of two well logs through one dual sliding window. The first sliding window (Win₁) moves top-down on the reference well log (GR₁), while the second sliding window (Win₂) moves up and down on the target well log (GR₂, ρ, ϕ_CNL, etc.) based on the signal sequence within Win₁, to extract target sequences with similar features to the reference well log. In the DDQN algorithm architecture shown in Fig. 3, the center point of the sliding window represents its current depth position on the well log. The first sliding channel of the dual sliding window contains a feature sequence of length (l) on the reference well log, with the window size covering 128 sampling points at a sample interval of 0.125 m; the other channel covers a sequence of the same length on the target well log. Given that a fixed-size sliding window may not easily capture smaller or larger feature sequence segments due to its constant size, this study introduces a variable sliding window. An agent can select a random size through trial and error to find the appropriate feature capture window, as defined in Eqs. (3) and (4). To visually represent the sliding window channels, a segment is cut from the well log (see the red box in Fig. 4), with the size of the first sliding window defined in Eq. (3) as Win₁. The initial position of the center point of the second sliding window (Win₂) is the same as Win₁, with the window boundary size randomly generated by the agent. During the top-down sliding matching process, Win₂, as defined in Eq. (4), can identify the best matching features on the target well log.

Subsequently, the multi-agent system emulates humans to perform depth matching of multiple well logs based on the sequential decision-making process. This process divides each time step t into two steps. The first step is mainly to complete the matching task between the GR well logs measured at different stages within the same well. That is, first set the depth delay of the sampling points on the well logs (GR₂, ρ, ϕ_CNL, etc.) recorded in the second stage in the same well as the same as preset value, ensuring that the depth of the well logs in the second stage is roughly consistent ^[25]. Then, while matching GR₂ with the reference well log GR₁, preliminary depth matching is also conducted between well logs ϕ_CNL, ρ, etc., and GR₁. The second step is mainly to fine-tune the depth deviation between the target well logs and GR₁ when the depth discrepancies between different types of well logs within the same well cannot be overlooked.

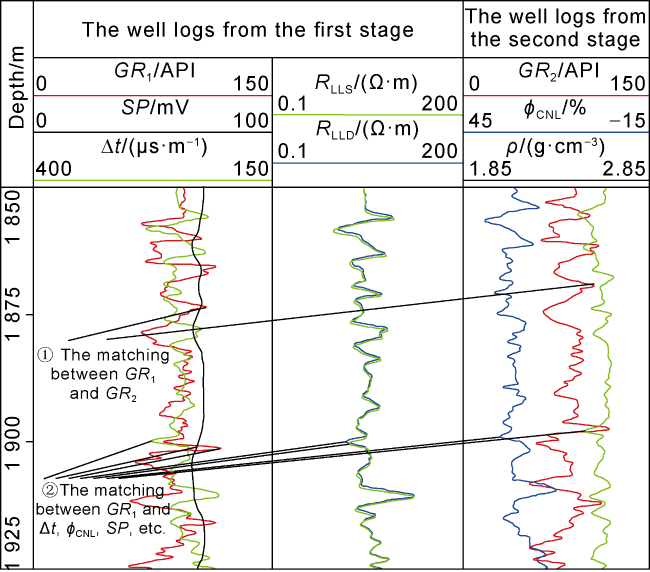
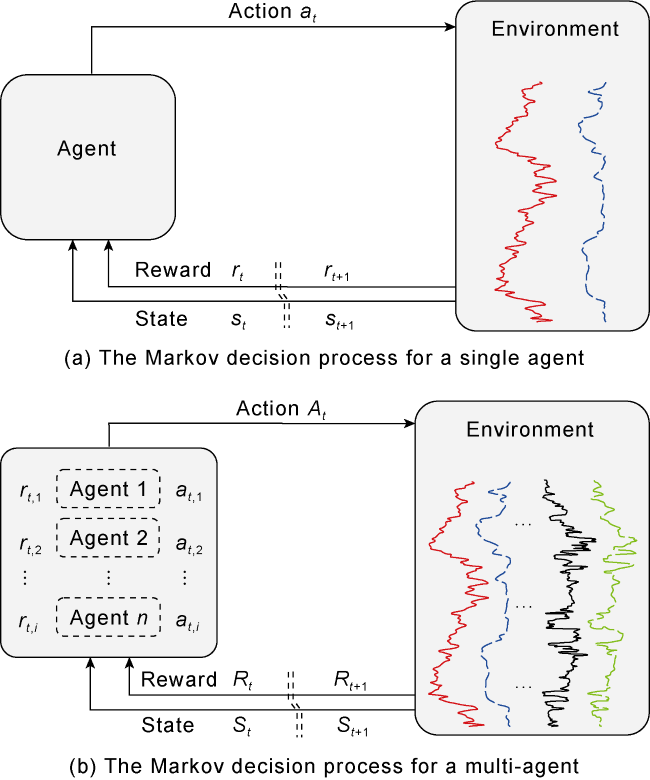
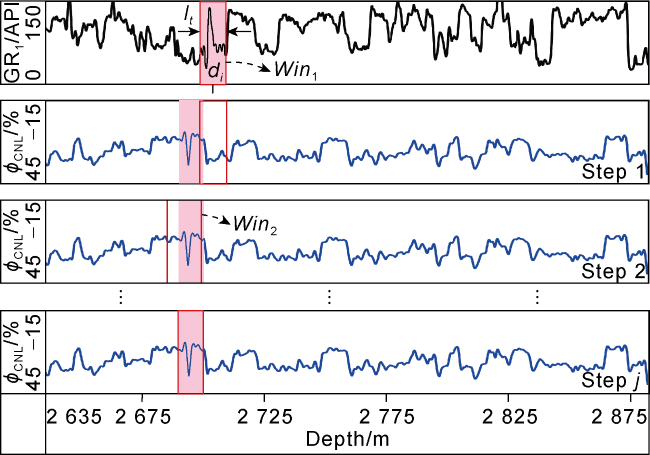
In this way, in the multi-agent depth matching task, each agent at time t obtains a depth matching state by observing the feature sequences of well logs through the dual sliding windows. The first type of agent responsible for the depth matching between GR well logs makes decisions in a predefined order, that is to choose an action ( a_{t,i}) based on the ε-greedy strategy ^[26] to act on the environment. Subsequently, the second type of agent, responsible for depth matching between the well logs ϕ_CNL, ρ, Δt, etc., and GR₁, selects an action a_{t,i} based on the decision-making result of the first type of agent to act on the well log to be matched. At time t, each agent can update to the next state (s') and receive a feedback reward (r) after interacting with the environment. Then the experience replay pool (D_t) collects and stores the experience samples (s,a,r,s\text{'}) of agents at each time t. 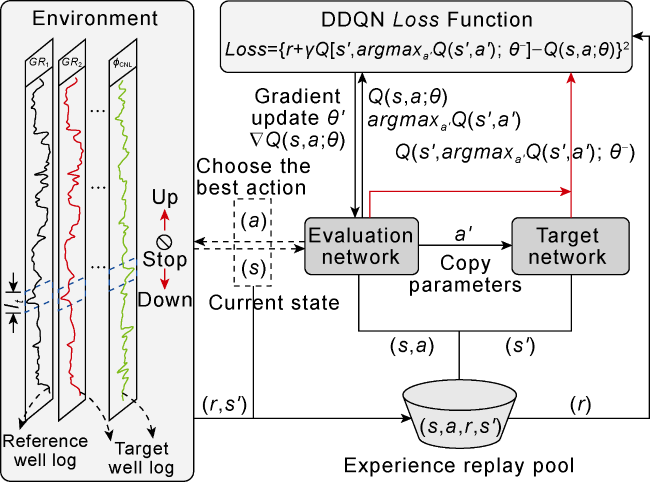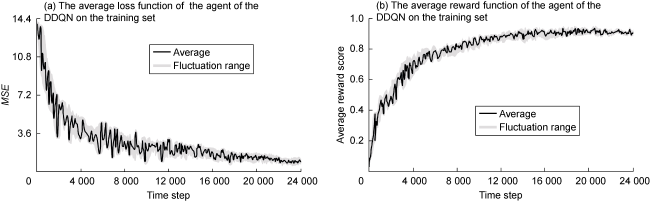As shown in Fig. 3, during the model training process, DDQN randomly selects a batch of sample data from D_t. 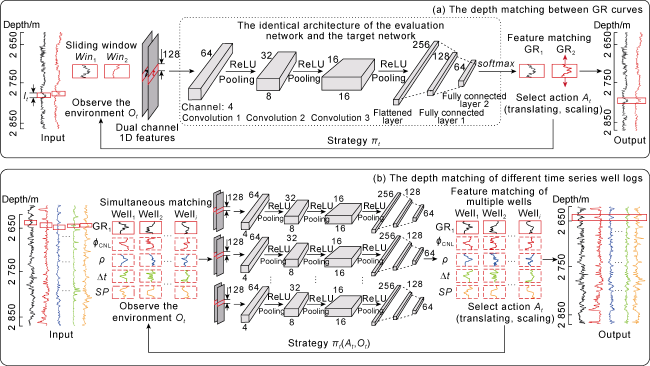It calculates the Q-value Q(s,a;θ) for the selected action (a) in the current state through the evaluation network, and estimates the Q-value Q(s\text{'},a\text{'};{\theta }^{-}) of selected action (a') in the next state through the target network. This dual-network structure has the same architecture, and includes three convolutional layers (Fig. 4), with each convolutional layer followed by a nonlinear activation function (ReLU) and a max-pooling layer, and the features are integrated through a fully connected layer to output the Q-values. Then, the difference between the Q-values of the evaluation network and the target network under the current strategy is calculated through a loss function (Eq. (5)). By minimizing the loss function, it is used to guide the optimization of the neural network, thereby learning a better matching strategy. Finally, the current evaluation network parameter (θ) is updated to θ' through a stochastic gradient descent (Eq. (6)) for the next round of training and learning. By repeating the above process, each agent can learn how to take the optimal action to complete depth matching for multiple well logs.

In the model evaluation task, this paper uses a matching correlation coefficient (R), a mean absolute error (MAE), a mean squared error (MSE), and a coefficient of determination (R²) as metrics to assess the predictive performance, as defined in Eqs. (11)-(13). The matching correlation coefficient measures the degree of similarity in feature sequences between well logs, with a value range of −1 to 1 ^[30]. The R-value approaching 1 indicates perfect match of feature sequences, 0 denotes no correlation between sequences, and −1 indicates negative correlation ^[30]. When MAE and MSE are smaller and R² is larger, the matching effect between target well log and reference well log is better.

An anticlinal structural and fault block reservoir in the central and eastern part of S oilfield in the SL Basin in Northeast China was taken as the research area. A total of 118 well logs were collected from 16 wells in the L area of the fault block without depth matching. The data were randomly divided into a training set and a test set by a 3-to-1 ratio in terms of the number of wells. The training set includes 91 well logs from 12 wells and the test set includes 27 well logs from 4 wells. Each well has eight conventional well logs (GR₁, GR₂, SP, Δt, ϕ_CNL, ρ, R_LLS and R_LLD). Except for a few wells missing SP, each well log has 5 000 to 22 000 sampling data points. In this paper, multi-agent deep reinforcement learning means to use multiple agents to process the well logs from different wells respectively. Since the object of model training and learning is the feature sequence within the sliding window on the well log, multi-agent deep reinforcement learning (MARL) can effectively handle the inconsistent number of well logs from different wells and has high flexibility. Subsequently, the divided training set was used to train the multi-agent reinforcement learning model for 1 000 rounds (Fig. 3). During the training process, a grid search method was used for model tuning to obtain better model learning performances using the model parameters in Table 1. In addition, an experience replay pool with a size of 1×10⁶ should accommodate as many training samples as possible to achieve better training performances. The ε-greedy strategy in the DDQN model served as a balanced approach between exploration and exploitation ^[27], with its ε value set to decay gradually from 1.0 to 0.1 by an increment of 1×10⁻⁵. After the model was trained, it was used to predict the depth matching results on the test set.

The matching of similar features on multiple well logs is a process that captures similar feature sequences between well logs through a double sliding window (Fig. 5). The first sliding window (Win₁) moves top-down on the reference well log (GR₁) and stops at depth (d_i) at time step t, where the feature sequence (l_t) within the sliding window serves as the reference feature. Then, another variable sliding window (Win₂), based on the score of the correlation coefficient fed back from the interaction between the agent and the environment, moves up and down on the target well log (GR₂, ϕ_CNL, etc.) to find a feature sequence similar to l_t. Since the depth correction between well logs is usually less than 30 m, Win₂ is set to move up and down within a depth range of (d_i±30 m) on the target well log, instead of across the entire well log. If the matching coefficient score between two feature sequences is greater than the preset threshold (0.9), they are considered successfully matched; otherwise, the sliding window will continue to move up and down for matching. If the agent observes that no similar feature sequence is found within the depth range (d_i ±30 m) of the target well log, both sliding windows will abandon the segment and move on to capture the next similar feature (l_t+1) of the depth (d_i+1). The first sampling point of the uncaptured feature segment will automatically align to the last sampling point of the previous feature segment (d_i) and be fine-tuned through a scaling action according to the length of the reference well log to complete the depth matching. In essence, not all similar feature segments need to be identified in the depth matching process. Instead, it involves using a CNN to quantify the matching probability between two different well logs, so that the most representative similar feature sequences can be captured. In the application in the L area of S Oilfield, the average matching accuracy (R) between GR₂ and GR₁ on a separate test dataset reached 88.25%. The matching accuracy and standard deviation (σ) of other well logs are listed in Table 2. Generally, the matching accuracy between GR₂ and GR₁ is relatively high, and the standard deviation is comparatively low, followed by SP, ϕ_CNL, R_LLD, R_LLS, ρ, and Δt. The possible reason is that the same physical measurements are recorded by GR₂ and GR₁, and the feature information on the same geological background is more similar. In contrast, other well logs (ϕ_CNL, Δt, etc.) measure completely different physical quantities from GR, relying on potential feature correlations under the same geological conditions for depth matching. Once a similar target depth segment (d_i) is captured between multiple well logs, the agent observes the current matching state s in the environment and selects the optimal action (translating or scaling) to update to a new state s\text{'}. If the agent calculates that the difference (MSE) between the depth of the current reference well log and that of the target well log falls below the preset threshold (0.05) and does not further decrease significantly, the feature sequence can be considered to have a better matching effect, otherwise starting the next round of matching.

A one-dimensional CNN sliding window convolves the feature sequences on well logs and inputs them into the MARL model for learning. After multiple rounds of training, the trained model is used to predict depth matching on a new test set. Fig. 6a shows the training performance of the agent in the environment, where the training error rapidly decreases in the initial stage and gradually diminishes and stabilizes in later stages. This indicates that the model has quickly learnt to utilize the optimization strategy for depth matching through feedback signals in the initial stage, and it’s finely tuned in the subsequent stages. The decreasing value and amplitude of the loss function learned by the agent in the environment suggest improved learning effectiveness. Fig. 6b displays the reward function obtained during the training process on the training set, reflecting the optimization effect of the depth matching task. The reward function starts at a lower value, gradually increases over time steps, and eventually stabilizes around 0.834, indicating that the correlation between the predicted depth of the well log and the real depth is gradually enhanced in the process of training the model, and the learning effect is better. Fig. 7 illustrates the depth matching prediction result for Well L1-11 in S Oilfield. Comparing the depth differences between the original and matched well logs, the DDQN algorithm successfully captured the most similar feature sequences on the target well logs (GR₂, ϕ_CNL, ρ, etc.) and the reference well log (GR₁). The corrected target well logs are well aligned with the reference well log, especially in the significant feature sequences (Fig. 7). The red boxes at the same depth positions on the well logs in Fig. 7 illustrate the significant effect of depth matching before and after using the DDQN algorithm, indicating that the well logs have been improved after DDQN depth matching.

Taking another well, L1-10, as a case, we compared the depth matching prediction results of DTW, DQN, and DDQN methods, and the manual matching results through CIFLog software. The prediction results before and after depth matching between GR₂ and GR₁ are depicted in Fig. 8, while the depth matching results between ϕ_CNL and GR₁ are shown in Fig. 9. As can be seen from Figs. 8 and 9, the DDQN captured significant similar feature sequences (in the red boxes) on the target well logs (GR₂, ϕ_CNL) and the reference well log (GR₁). Moreover, the overall predicted matching effect by DDQN is better than manual matching, DTW and DQN, and reducing the manual intervention. The depth matching effect of GR in Fig. 8 is better than that of ϕ_CNL in Fig. 9, maybe due to GR and ϕ_CNL measuring different physical properties of the formation. GR measures the content of natural radioactive elements, whereas ϕ_CNL measures the hydrogen content in formation. These two types of properties have discrepancy in physical signals. All GR logs record the same parameter of natural radioactivity, making similar physical signals easier to be captured. Fortunately, the DDQN algorithm can capture most similar feature sequences, so its matching accuracy is high (Fig. 9). DTW performs well on simple feature sequences, but struggles with complex sequences, especially those with strong nonlinear features (at depth around 3 055 m and 3 140 m in Fig. 8). Although DQN performs better than DTW on the sequences with significant changes in the nonlinear feature, the former is still affected by overestimation of the Q-value, resulting in slight discrepancies between the target and the reference well logs (at depth near 3 055 m in Fig. 8 and 2 965 m in Fig. 9). All the prediction models used in this study were run on a computer with a 4.90 GHz Intel i7-12700 CPU and an NVIDIA GeForce 3 080 graphics card. As shown in Table 3, DDQN spent longer time than DQN, which is 23.26 min and 16.53 min, respectively. Table 3 also summarizes the evaluation results of similar features captured by different methods based on dual sliding window after depth matching on the test set. The statistical prediction results in Table 3 indicate that all the methods generally achieved good depth matching effects, but R, MAE, and R² of the DDQN method are superior to those of DQN and DTW. The prediction effect of DQN on the test set still lags behind DDQN, with minor discrepancies between the target well log and the reference well log near complex feature segments in Figs. 8 and 9, suggesting that DDQN performs better than DQN in matching effects and error reduction.