Introduction
In-situ stress, a state of stress existing in the body of rock, is not only one of the main parameters that affects the geological and engineering plan and their implementation[1,2], but also a basic one that has to be considered in the plan of fracturing stimulation and in the well pattern design for low permeability reservoirs[3,4,5,6]. For the reservoir with low permeability (with a buried depth of usually more than 2 000 m), reservoir geomechanics mainly studies the state of stress in the low permeability reservoir, and it has been making progress with the development of low permeability reservoirs both in China and abroad, and especially, the development of unconventional tight oil and gas[7,8,9,10]. Its theory has partly succeeded to the tectonic stress theory. Under the guideline of tectonic stress theory, reservoir geomechanics pays attention to the characterization of structural features of reservoir, and meanwhile the geological body of reservoir is considered as a homogeneous mechanical parameter body, and only mechanical parameters in the fault zone are handled according to experience, so the conclusion is often that the stress distribution of reservoir (generally with an area of 0.5-3.0 km2) is controlled by structure, and that the stresses are nearly uniform in direction and mainly controlled by buried depth [11,12,13]. Some scholars have realized the influence of sedimentation and diagenesis, i.e. there are differences in lithology, mineral component and texture, upon which different types of rocks with clearly different mechanical properties can be classified[14,15,16,17]. These differences, combined with structural complexity, will lead to great degree of stress heterogeneity, but at present the number of published documents about the influence of mechanical property on in-situ stress is limited. JING Feng et al.[18] studied the stress of sedimentary, igneous and metamorphic rocks, and found that the stress magnitudes of different rocks had different relationships with buried depth. QIN Xianghui et al.[19], and PEI Qitao et al.[20] conducted laboratory experiments and found that mechanical parameters such as Young's modulus and bulk modulus had influence on the magnitude of stress. TEUFEL L W[21] measured stress in flat-lying, tight gas sandstone reservoirs and bounding mudstone formations of the Mesaverde Group in the Piceance Basin of Colorado, and found that the principal horizontal stress magnitude didn’t increase linearly with depth, but was closely related to lithology. Based on this, he proposed that lithology was an important factor affecting the stress heterogeneity of reservoir. ZU Kewei et al.[22] used finite element simulation to study the influence of mechanical differences between sandstone and mudstone on in situ stress. Previous researches mainly used various measurements, numerical simulations to directly observe the phenomenon that different rocks corresponded to different stress states, but didn’t investigate the underlying mechanism. To understand how different rocks influence in situ stress of reservoir and to reveal the corresponding mechanism can not only advance the geomechanics theory of reservoir, but provide a theoretical foundation for how to understand and use the phenomenon that different rocks have different stress states.
Since 2012, the in-situ stress of reservoirs and its heterogeneity have been studied in the Shengli Oilfield and it was found that the distributive complexity was not caused only by local features of regional tectonic stress field. Therefore, in the process of study, the discriminative treatment has to be applied to the reservoir geomechanics and regional tectonic mechanics. Taking the Bonan Oilfield, located in the Zhanhua Sag of the Jiyang Depression, as an example, this paper, based on triaxial compression tests of analyzing the mechanical difference of rocks, investigates the mechanism and laws of the influence of mechanical variation of rocks on the in situ stress of reservoirs. We hope that the study results can provide guidance for field operations, touch off discussions on in-situ stress heterogeneity, and intrigue more research on in-situ stress heterogeneity of reservoirs.
1. An overview of regional geology
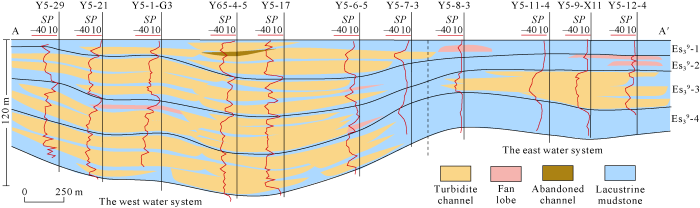
The Bonan Oilfield is located in the middle of the Zhanhua Sag of the Jiyang Depression, where the strata from the top downwards consist of Pingyuan Formation of Quaternary, Minghuazhen and Guantao Formations of Neogene, and Shahejie and Kongdian Formations of Paleogene. Area 5 of Bonan Oilfield, located in the southeast of the field (Fig. 1), is dissected by approximately west-east V-shaped faults. In Area 5, Es39 of the third member of Shahejie Formation of Paleogene is typical deposits of turbidite fan in a fault-depression basin. Two water systems can be recognized: the western system is composed of well-developed turbidite sand bodies, mainly fine sandstone; while eastern system is composed of poorly developed turbidite channel deposits, and especially lacustrine mudstone (Fig. 2). The reservoirs have an average permeability of 20.5×10-3 μm2, a middle buried depth of 3200 m and an average formation temperature of 92 °C, typically comprising low-permeability oil pools in Zhanhua Sag.
Fig. 1.
Fig. 1.
Regional structure map of Bonan Oilfield.
Fig. 2.
Fig. 2.
Cross section showing sedimentary microfacies distribution of turbidite fan in Area 5 of Bonan Oilfield (SP—spontaneous potential, mV; Es39-1,2,3,4—No.1,2,3,4 subzones of No.9 sandstone zone of the third member of Shahejie Formation, Paleogene).
Lots of measuring data of in-situ stress in Jiyang Depression have proved that “the greatest stress is the vertical stress, the smallest is the minimum horizontal principal stress, and the maximum horizontal principal stress is in between”, suggesting a typical tensional stress environment. The WSM database Release 1997 show that Jiyang Depression is influenced by the Pacific Plate movement and the direction of the current regional maximum horizontal principal stress is nearly east-west.
2. Influence of the mechanical property differences of rocks on in-situ stress of reservoirs
2.1. Mechanical property differences of rocks
In this study, the mechanical property differences of rock samples were analyzed by triaxial compression test. In the test, 4-7 rock samples, 25 mm in diameter and more than 50 mm in length of the same lithology were collected from the nearly same depth (with depth difference of less than 200 m). Thin section observation showed that the rock components mainly include quartz, feldspar and rock debris, belonging to lithic arkose or feldspathic litharenite. The tests were done with the GCTS Triaxial Rock Testing Systems (RTX-3000). In order to make the test conditions closer to the geological conditions of underground reservoirs, the rock samples were fully saturated with water, and then sealed with sealing films to retain the fluid[23]. Rock mechanics parameters are also influenced by temperature. According to LI Xiaoshuang’s test on coarse sandstone[24], P wave velocity progressively decreases only by 3% at 100 °C. Considering the fact that the reservoir temperature in Bonan Oilfield is about 92 °C, the temperature’s influence is negligible in this test. The tests were done on samples with same lithology at room temperature and under triaxial confining pressure of 32 MPa[25] to obtain their Young's modulus and Poisson’s ratio under the subsurface reservoir conditions (Table 1). The confining pressure of 32 MPa was selected because many experiments prove that the mechanical parameters of low-permeability sandstone remain basically unchangeable in Bonan Oilfield when the confining pressure is greater than 25 MPa[26].
Table 1 Mechanical parameters of different lithofacies in low- permeability reservoirs, Bonan Oilfield.
| Lithology | Num- ber | Poisson's ratio | Young's modulus /GPa | ||||
|---|---|---|---|---|---|---|---|
| Maximum | Minimum | Average | Maximum | Minimum | Average | ||
| Coarse sandstone | 4 | 0.225 | 0.216 | 0.219 | 29.50 | 29.31 | 29.43 |
| Fine sand- stone | 7 | 0.198 | 0.189 | 0.193 | 26.81 | 26.52 | 26.70 |
| Siltstone | 4 | 0.279 | 0.258 | 0.267 | 26.22 | 25.13 | 25.69 |
| Mudstone | 4 | 0.372 | 0.361 | 0.366 | 16.34 | 15.42 | 15.97 |
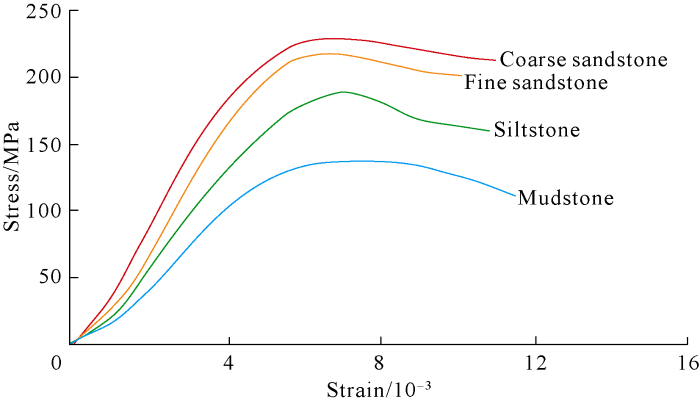
The test results suggest that under the subsurface reservoir conditions (reservoir pressure and water saturated) different lithofacies of Es39 in Bonan Oilfield show big difference in mechanical parameters (Table 1). Generally, as the grain size decreases, the Poisson’s ratio increases but Young's modulus decreases. Under reservoir conditions different lithological samples differ widely in stress-strain relationship too (Fig. 3), especially sandstone and mudstone. Before breaking, the sandstone has dominantly linear elastic deformation, while mudstone only goes through a short period of linear elastic deformation, then undergoes an obvious process of high-pressure plastic deformation, showing the characteristics of elasto-plastic deformation.
Fig. 3.
Fig. 3.
Stress versus strain of rock samples from laboratory test.
2.2. Mechanisms of the influence of rock mechanical property difference on in-situ stress
2.2.1. Evidence for the existence of extra stress at lithological interface
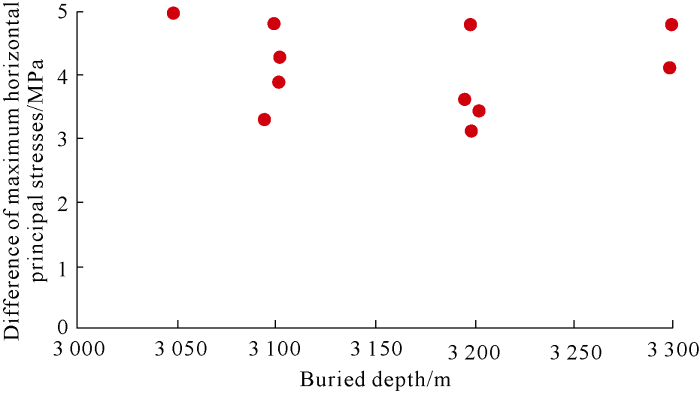
The statistics of maximum horizontal principal stresses of sandstone and mudstone very next with each other in Es39 calculated from XMAC data suggest that the sandstone and mudstone have an obvious difference of maximum horizontal principal stress of 3-5 MPa, which is not related to buried depth (Fig. 4). Therefore, a triaxial compression test was designed to measure the axial stress on the lithological contact surface using RTX-3000 at room temperature under a confining pressure of 32 MPa and an axial pressure of 60 MPa. The sample was a combination of a water-saturated fine sandstone plug (25 mm long) and a water-saturated mudstone plug (25 mm long). The results show that the axial stress is 64.63 MPa at the lithological contact surface, 4.63 MPa greater than the axial pressure. This part of stress, derived from both XMAC data and laboratory test, is defined as “extra stress” in this paper, denoted by β.
Fig. 4.
Fig. 4.
Maximum horizontal principal stress difference between sandstone and mudstone versus buried depth.
2.2.2. Generation mechanism of the extra stress
In the lab experiments, the conditions are all the same for the sandstone and mudstone, except for their mechanical properties. XMAC data were also measured under the same conditions, and even the calculation methods are identical. Meanwhile, other conditions such as geological structure, formation temperature and overlying pressure are almost the same, only except for the mechanical properties of mudstone and sandstone. Consequently, the stress difference between mudstone and sandstone, either in laboratory test or according to the calculation using XMAC data, can only be caused by their mechanical property difference. This conclusion can also be proved by the fact that the stress difference derived from XMAC data isn’t related to the buried depth.
Compared with the whole sedimentary basin, the geological body of reservoir is very limited in scale, and its boundary condition of deformation is also limited and can be approximated as a rigid boundary condition. According to Fig. 3, under the same stress, the deformation amount of mudstone is so large that the mudstone will inevitably compress the sandstone; as a result, at the interface, there occurs a pair of acting and reacting forces besides the boundary stress. The acting force is the “extra stress” in this paper. The extra stress is directed towards the sandstone while the reacting force is towards mudstone. In the whole area comprised of mudstone and sandstone, both acting and reacting forces are internal force, but as to sandstone the extra stress is an external force that should not be neglected. Therefore, this paper holds that the regional tectonic stress is different from the reservoir’s in-situ stress, and the extra stress won’t have any influence on the state of tectonic stress, but it will influence the state of in-situ stress within the reservoir. Under reservoir conditions, the physical essence of the generation of extra stress is that the mechanical difference between complex geological bodies leads to a discontinuous surface of mechanical property. On both sides of this discontinuous surface, the deformation characteristics and amount of geological bodies cause the extra stress, just as the obvious difference between the stresses inside and outside a fault zone where Young's modulus reduces and Poisson’s ratio increases. These are the preliminary understandings about the generation mechanism of extra stress in this paper, which has not been proved by tests. Therefore, the generation mechanism of extra stress needs to be studied further.
2.2.3. Estimation method of extra stress
According to rock mechanics theory, the following hypotheses are put forward: A. rigid boundary condition; B. the same stress boundary conditions for sandstone and mudstone; C. deep buried reservoirs with high overlying pressure. Under the free boundary condition, let σ, εm and εs stand for stress, deformation amount of mudstone and deformation amount of sandstone, respectively.
Under free boundary and same stress conditions, the deformation amount of mudstone is larger than that of sandstone, while under rigid boundary and same stress conditions, the deformation amounts of mudstone and sandstone are approximately equal. Therefore, under the rigid boundary conditions, the sandstone blocks the mudstone deformation, so that the deformation amount of mudstone is reduced by Δε:
Δε corresponds to the extra stress β that mudstone acts on sandstone:
Therefore, the extra stress βis influenced by the difference of deformation amount between different rocks. The larger the rock deformation amount difference, the larger the extra stress β is.
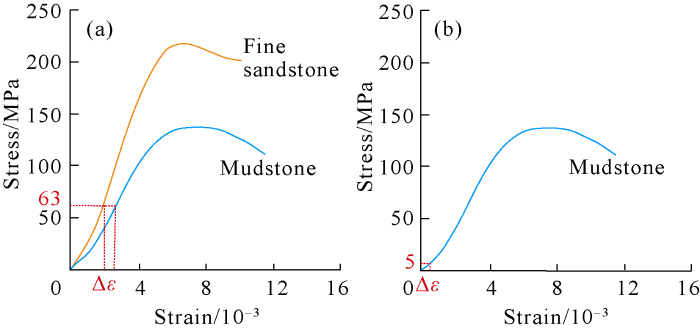
The stress-strain curve of mudstone sometimes doesn’t conform to typical linear elasticity, i.e. Young's modulus of mudstone varies with the stress applied. Thus the extra stress can be estimated according to typical stress-strain curve obtained from triaxial compression test. The average horizontal principal stress of Es39 in Bonan Oilfield from acoustic emission measurement is 63 MPa. Firstly, according to stress- strain relationships between sandstone and mudstone, we estimated the Δε between sandstone and mudstone at 63 MPa under the laboratory conditions (Fig. 5a), and then we projected Δε onto the stress-strain curve of mudstone to obtain the corresponding value of extra stress, β (Fig. 5b). Using the above diagram method, the extra stress of Es39 in Bonan Oilfield was estimated at 5 MPa, which has an error of 0.37 MPa from that of the laboratory measurement, and is approximately equal to the value derived from XMAC data.
Fig. 5.
Fig. 5.
Diagrams of estimating extra stress with stress-strain curves.
2.2.4. Mechanical mechanism of how extra stress affecting in-situ stress of reservoir
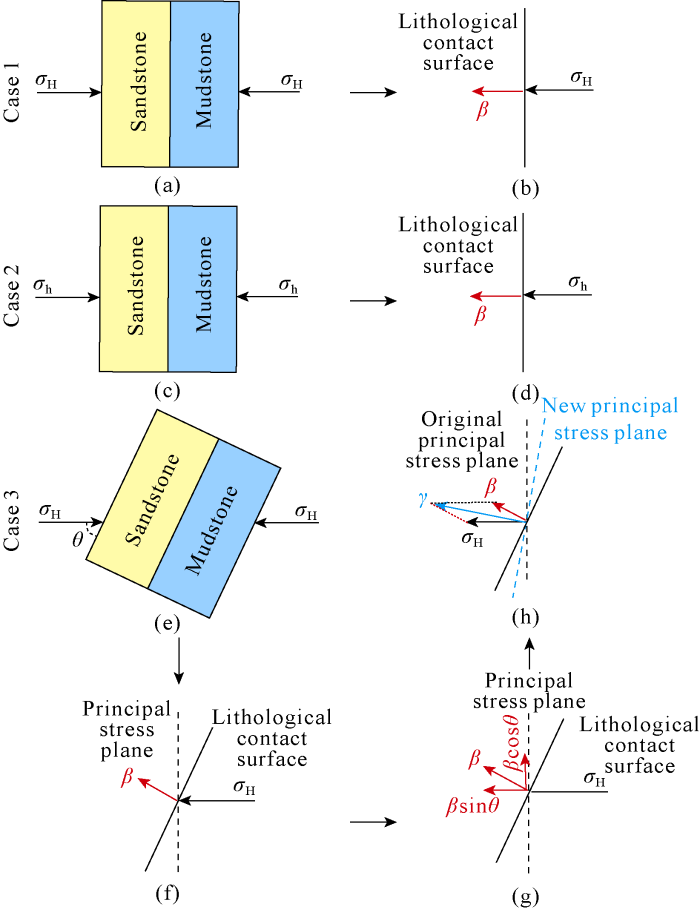
Subject to sedimentation and subsequent tectonic movements, geological bodies are complex in sandstone occurrence and morphology. We can classify the relationships between lithological contact surface and the direction of boundary maximum horizontal principal stress into the following three cases in geometry: perpendicular, parallel and oblique crossing (Fig. 6). Without considering the influence of geological structure on in-situ stress: when lithological contact surface is perpendicular to the direction of boundary horizontal maximum principal stress (Fig. 6a), the horizontal stress field strength within the reservoir changes because of the influence of extra stress on lithological contact surface, but the direction of stress field doesn’t change (Fig. 6b); when the lithological contact surface is parallel with the direction of boundary maximum horizontal principal stress, i.e. perpendicular to the direction of boundary minimum horizontal principal stress (Fig. 6c), if the extra stress is low, the direction of stress field in the reservoir doesn’t change but the minimum horizontal principal stress increases (Fig. 6d); if the extra stress is high enough to cause the horizontal stress field to change direction by 90°, the maximum horizontal principal stress in sand body would change into the minimum horizontal principal stress. When lithological contact surface is oblique to the direction of boundary maximum horizontal principal stress (Fig. 6e), the extra stress causes shear stress to occur on the boundary horizontal principal stress plane, and meanwhile the horizontal principal stress increases (Fig. 6h). According to the definition that there is no shear stress in the plane perpendicular to the direction of principal stress in stress principal coordinates system, it can be concluded that the stress principal coordinates system in the reservoir has rotated, and that the principal stress in the reservoir has changed, creating a new stress field (Fig. 6g).
Fig. 6.
Fig. 6.
Illustration of the mechanism of how mechanical property difference affects stress field.
To summarize, without considering the influence of geological structure on in-situ stress, the existence of extra stress on lithological contact surface will cause changes of magnitude and direction of horizontal principal stress in sand body. The variation degree of stress magnitude and direction are controlled by the degree of mechanical property differences of rocks on both sides of lithological contact surface and the angle between the lithological contact surface and the direction of the boundary principal stress jointly.
2.3. Influence of extra stress on in-situ stress of reservoirs with stress ellipse
The influence of the angle between lithological contact surface and the direction of boundary horizontal maximum principal stress on the stress field in reservoir can be analyzed by stress ellipse. When the angle between the lithological contact surface and the direction of boundary maximum horizontal principal stress ranges from 0° to 90°, the lithological contact surface rotates in the quadrant I (Fig. 7). According to geometry, the component βσ of extra stress β on the lithological contact surface can be expressed in the direction of any arbitrary boundary horizontal stress σ as follows:
Fig. 7.
Fig. 7.
Illustration of the stress ellipse.
According to standard elliptic equation, we use the following equation to express the boundary stress ellipse:
Therefore:
The magnitude of any arbitrary stress on boundary stress ellipse can be expressed as:
According to equations (3) and (4), through the trigonometric function transformation we get:
Putting (3) into trigonometric function transformation, we get:
According to (5) and (6), the relationship between any arbitrary stress σ and α is expressed as:
Combining (1) and (7), we obtain σ°:
where, σ° is any arbitrary stress on stress ellipse caused by the influence of mechanical property difference in reservoir.
It is apparent from equation (10) that without considering the influence of structure on in-situ stress, the stress field in the reservoir is controlled by boundary stress (σH, σh), extra stress (β) and the angle (θ) between lithological contact surface and the direction of boundary maximum horizontal principal stress. If the reservoir buried depth varies slightly, the boundary stress conditions of the reservoir can be considered to be certain. Then the shape of the stress ellipse is mainly controlled by the degree of rock mechanical property difference and the angle between lithological contact surface and the direction of boundary maximum horizontal principal stress, which agrees with the conclusion from the geomechanics analysis.
A combination of mechanical analysis and mathematical analysis of stress ellipse reveals that the degree of rock mechanical property difference influences the extra stress (β), and the extra stress changes the state of the stress field in the reservoir. This is the mechanism of how mechanical property difference of rock influences the in-situ stress field in the reservoir.
3. Influence of rock mechanical property difference on in-situ stress field
3.1. Variation rules with stress ellipse
According to equation (11), under definite boundary conditions, we studied how the angle (θ) between lithological contact surface and the direction of boundary maximum horizontal principal stress and the rock mechanical property difference (extra stress, β) influenced the stress field. According to the statistics in Jiyang Depression, we established the relations between the buried depth of low-permeability reservoir and the magnitude of the horizontal stresses as follows:
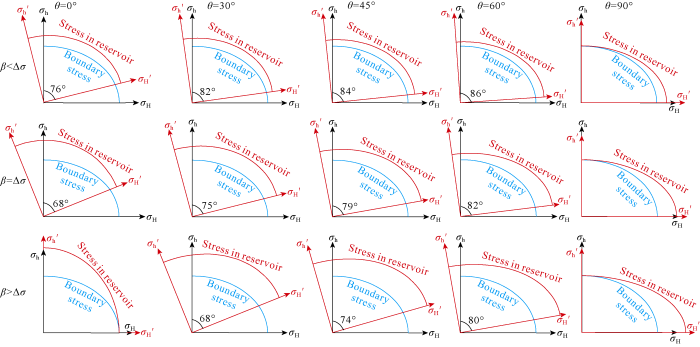
In order to clearly see the stress ellipse’s shape, the boundary maximum horizontal principal stress was assumed to be 80 MPa, the boundary minimum horizontal principal stress σh to be 60 MPa, and then the stress ellipse shapes θ is 0°, 30°, 45°, 60° and 90° and β<Δσ, β=Δσ and β>Δσ (Fig. 8) were discussed.
Fig. 8.
Fig. 8.
Influence of rock mechanical property difference on in-situ stress field.
According to Fig. 8, the mechanical property difference of rock has such influences on in-situ stress field in reservoir as: A. when θ=0°: if β<Δσ, the horizontal stress field in the reservoir changes little, so does the maximum horizontal principal stress, but the minimum horizontal principal stress increases markedly; if β=Δσ, the horizontal stress field in the reservoir changes direction greatly, the maximum horizontal principal stress increases a little, and the minimum horizontal principal stress increases markedly, but the horizontal stress difference is very small; if β>Δσ, the horizontal stress field in the reservoir changes direction by 90°, the boundary maxi-mum horizontal principal stress changes direction to that of the minimum horizontal principal stress, and the minimum horizontal principal stress is nearly equal to the boundary maximum horizontal principal stress. B. when θ=90°: regardless of the relationship between β and Δσ, the horizontal stress field in the reservoir changes direction very little, the value of maximum horizontal principal stress increases as β increases, and the minimum horizontal principal almost remains unchanged and approximately equal to that of the boundary minimum horizontal principal stress. C. when 0<θ<90°: if there is a definite relationship between β and Δσ, the maximum horizontal and minimum principal stresses of the stress field in the reservoir both increase to some degree, compared to the corresponding boundary ones, and their directions also change a little. In general, as θ increases, the angle of rotation increases and then decreases, the maximum horizontal principal increases and the minimum horizontal principal stress decreases. D. when 0<θ<90°: if θ is a constant, as β increases, the rotation angle of stress field in the reservoir increases, the maximum and minimum horizontal stresses also increase, but the difference between them decreases continuously.
3.2. Analysis of variation rules by numerical simulation
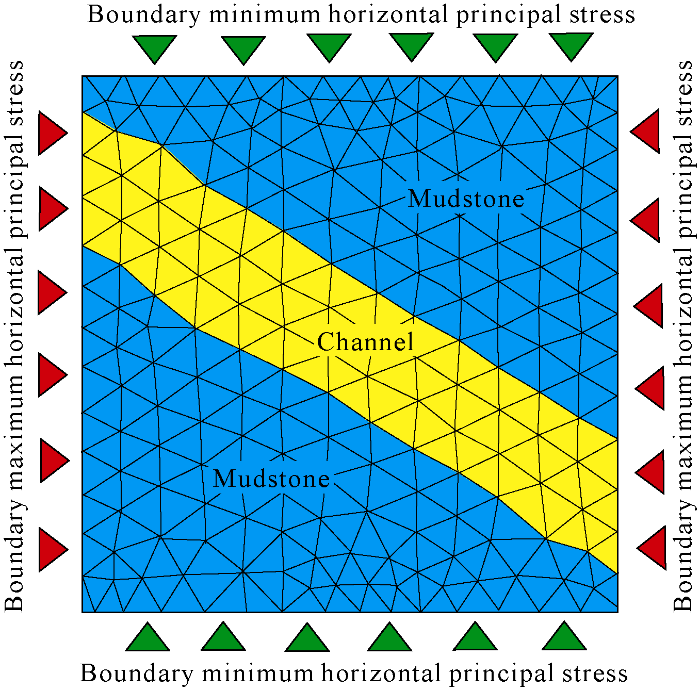
Based on the stress ellipse analysis, taking the low-permeability reservoir of Bonan Oilfield in Jiyang Depression as an example, the influences of rock mechanical property difference and the angle between lithological contact surface and the direction of boundary horizontal maximum principal on in-situ stress field were further studied using the plate model of the finite element simulator Ansys (Fig. 9). Elastic material was selected as the confining rock. Its mechanical parameters took those of mudstones of the low-permeability reservoir in Bonan Oilfield: Young's modulus E=15.97 GPa, Poisson’s ratio μ=0.366. The Young's modulus and Poisson’s ratio values of channel took the average values of coarse sandstone, fine sandstone and siltstone respectively (Table 1); and for argillaceous sandstone, it is assumed E=22 GPa, μ=0.32, considering channel as linear elastic material. Suppose σH=80 MPa, σh=60 MPa, considering the model boundary as rigid, pressure coefficient Cp=1.0, and pore pressure P=32 MPa.
Fig. 9.
Fig. 9.
Ansys plate model.
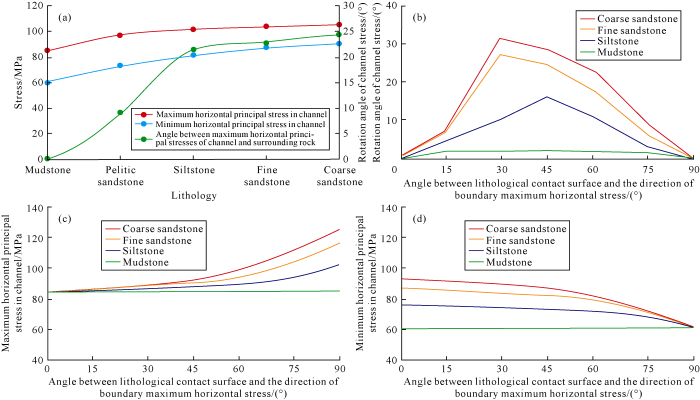
When analyzing the influence of rock mechanical parameters on stress field, we let the angle between the direction of boundary maximum horizontal principal stress and channel direction remain at about 40°, and assigned Young's modulus and Poisson's ratio values to the units within channel according to lithologies (Fig. 10).
Fig. 10.
Fig. 10.
Influence of rock mechanical property difference on stress field.
The results suggest that as the grain size of rock increases, both the maximum and minimum horizontal principal stresses in channel increase, which coincides with the rule that the larger the Young's modulus, the more easily stress occurs and also coincides with theoretical analysis, and the rotation angle of horizontal stress field in channel continues to increase (Fig. 10). The above findings confirm the mechanism and laws of the influence of rock mechanical property difference on in-situ stress field. When analyzing the influence of the angle between lithological contact surface and the direction of boundary horizontal maximum stress θ on the stress field, boundary conditions and mechanical parameters remain unchanged, and only the channel direction is changed. The results show that the rotation angle of the horizontal stress field in channel (Fig. 10b) increases with the increase of θ until reaching a maximum, then it decreases with the increase of θ until reaching the minimum “0”, when the lithological contact surface is perpendicular to the direction of the boundary horizontal maximum principal stress (Fig. 10b). The finer the grain size of rock in channel, the closer its mechanical properties are to the surrounding rocks, and the bigger θ becomes when the rotation angle of horizontal stress direction reaches its maximum (Fig. 10b). When θ is fixed at the same value, the more similar the rock mechanical properties of channel are to those of surrounding rocks, the smaller the rotation angle of stress direction is (Fig. 10b). For the same lithology, the maximum horizontal principal stress increases faster and faster as θ increases (Fig. 10c). With the same θ and different lithologies, the larger the grain size of rock, the greater the value of maximum horizontal principal stress is (Fig. 10c). For the same lithology, the minimum horizontal principal stress decreases with the increase of θ (Fig. 10d). For the same θ, the larger the grain size of rock, the greater the value of minimum horizontal principal stress is (Fig. 10d).
4. A case study
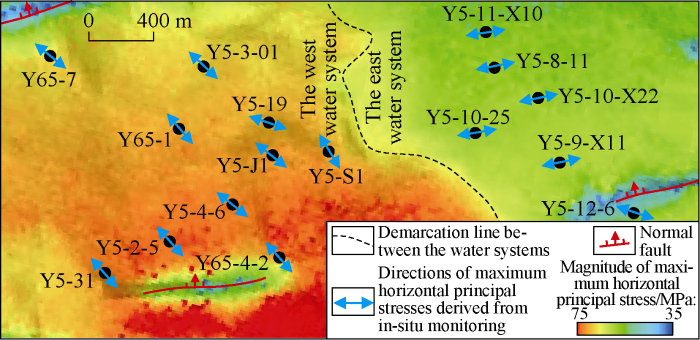
Based on XMAC data, microseismic monitoring data during hydraulic fracturing, wellbore sloughing data and acoustic velocity anisotropy data of Es39 in Bonan Oilfield, it is found that the maximum horizontal principal stress changes direction considerably in the west and east water system. In the east water system, the azimuth of maximum horizontal principal stress ranges from 72.3° to 86.4° with an average of 77.2°, while in the west water system the azimuth of maximum horizontal principal stress ranges from 113.7° to 135.0°, with an average of 123.6°. The angle between the directions of the maximum horizontal principal stresses in the two systems is 46.4° (Fig. 11). Based on the above results, we carried out finite element simulation on in-situ stress in Es39 of Area 5, Bonan Oilfield by taking geological structure and rock mechanical property variation into consideration (Fig. 11).
Fig. 11.
Fig. 11.
Distribution of horizontal maximum principal stresses in Es39 reservoirs of Area 5, Bonan Oilfield.
The simulation results show that the horizontal maximum principal stress directions in the east and west water systems has changed, coinciding with the measured data from drilling (Table 2). However, the above study results reveal that in Bonan Oilfield the rock mechanical property difference can change the stress direction by 30° at most, while the measured angle between the horizontal maximum principal stress directions in the east and west water systems is 46.4°, which indicates that the V-shaped fault system and the lithological changes in the west and east water systems have caused the rotation of the direction of maximum horizontal principal stress jointly.
Table 2 Comparison of measured and simulated horizontal maximum principal stresses in Area 5, Bonan Oilfield.
| Well | Measured max horizontal principal stress direction | Simulated max horizontal principal stress direction | Absolute error | Measured max horizontal principal stress value | Simulated max horizontal principal stress value | Relative error |
|---|---|---|---|---|---|---|
| Y5-10-25 | 65.0 | 69 | -4.0 | |||
| Y5-10-X22 | 69.6 | 70 | -0.4 | |||
| Y5-11-X10 | 72.9 | 65 | 7.9 | |||
| Y5-12-6 | 115.0 | 109 | 6.0 | |||
| Y5-19 | 115.0 | 120 | -5.0 | |||
| Y5-2-5 | 130.0 | 120 | 10.0 | |||
| Y5-3-01 | 130.0 | 123 | 7.0 | 63.4 | 60.50 | -4.6 |
| Y5-31 | 135.0 | 126 | 9.0 | |||
| Y5-4-6 | 120.0 | 127 | -7.0 | 65.5 | 67.19 | 2.6 |
| Y5-8-11 | 62.3 | 68 | -5.7 | |||
| Y5-9-X11 | 86.4 | 85 | 1.4 | 63.3 | 59.00 | -6.8 |
| Y5-J1 | 117.5 | 119 | -1.5 | 60.3 | 64.30 | 6.6 |
| Y5-S1 | 130.0 | 121 | 9.0 | |||
| Y65-1 | 113.7 | 120 | -6.3 | 60.7 | 63.10 | 4.0 |
| Y65-4-2 | 125.0 | 133 | -8.0 | |||
| Y65-7 | 120.0 | 121 | -1.0 | |||
| Y65-XG5 | 68.0 | 73 | -5.0 |
In summary, affected by complex distribution of geological bodies, rock mechanical property difference and tectonic features, the distribution of stress field in the reservoir is very complicated, which should be paid more attention to. At present, most commercial software uses finite element method or finite difference approach to carry out forward modeling of in-situ stress field distribution. But limited by computation capacity and algorithms, the geological framework model paid more attention to characterizing structural features than distribution of geological bodies with different mechanical properties. Most mechanical parameter models before were homogeneous, which led to the coincidence of horizontal maximum principal stress direction and regional tectonic principal stress direction, and little stress direction variation in the whole field. This kind of simulation model is applicable to regional tectonic stress simulation, but not to the in-situ reservoir stress simulation, because it can’t fully characterize the heterogeneity of local in-situ stress field. To some extent, this kind of results will mislead engineers in well pattern design, horizontal well’s design and drilling and hydraulic fracturing, etc. for low-permeability reservoirs, especially tight oil and gas reservoirs. Therefore, to guide the above mentioned activities, it is necessary to fully understand the fact that mechanical property difference of geological bodies will cause changes of in-situ stress field in the reservoir. In-situ stress simulation should use laboratory core test to find out the mechanical property difference between geological bodies. Geological model should preferentially characterize the distribution of different geological bodies in space. For sandstone-mudstone reservoirs, it is important to characterize the distribution of sand bodies. For different geological bodies, different mechanical parameters are selected to establish mechanical parameter models, if possible, 3-D heterogeneous mechanical parameter models, and proper constitutive equations should be applied to different geological bodies. Then the heterogeneous in-situ stress field can be obtained by finite element or finite difference simulation, which can provide accurate reference to reservoir engineering, drilling engineering and fracturing designs.
5. Conclusions
In Bonan Oilfield, sandstone has higher Young's modulus and lower Poisson's ratio, and can be considered as approximately linear elastic material; while mudstone has lower Young's modulus and higher Poisson's ratio, and can be considered as elasto-plastic material.
There exists an extra stress between the mudstone and sandstone in the third member of Shahejie Formation in Bonan Oilfield, the magnitude of which is influenced by the mechanical property difference between mudstone and sandstone. The reservoir in-situ stress is controlled by the extra stress and the angle between lithological contact surface and the direction of boundary principal stress jointly.
Under the same boundary conditions, when the angle between lithological contact surface and the direction of boundary principal stress is constant, as the rock mechanical property difference increases, horizontal stress field in the reservoir increases in rotation angle and magnitude, and the minimum horizontal principal stress also increases, but the difference between the maximum and minimum horizontal stress decreases; when the extra stress is constant, if the angle between lithological contact surface and the direction of boundary principal stress increases, the rotation angle of horizontal in-situ stress field in the reservoir increases and then decreases, the maximum horizontal principal stress also increases, but the minimum horizontal principal stress decreases.
Under the same boundary stress conditions, the coarser the granularity, the greater the maximum and minimum horizontal principal stresses in the reservoir and the rotation angle of horizontal maximum principal stress will be; when the angle between lithological contact surface and the direction of boundary principal stress is constant, the maximum and minimum horizontal principal stress increase as the rotation angle of maximum horizontal principal stress increases.
The in-situ stress in reservoir, with strong heterogeneity, is different from and more complicated than the regional tectonic stress.
Nomenclature
E—Young's modulus, GPa;
Em—Young's modulus of mudstone, GPa;
t— an angle used in trigonometric function expression of stress ellipse (2σH, 2σh are lengths of the axes, 2σH>2σh ), (°);
X—the direction of boundary horizontal maximum principal stress, (°);
Y—the direction of boundary horizontal minimum principal stress, (°);
α—the angle between the direction of any arbitrary boundary horizontal stress and the direction of boundary horizontal maximum principal stress, (°);
β—extra stress at lithological interface, MPa;
βσ—component of extra stress in the direction of any arbitrary boundary horizontal stress, MPa;
γ—resultant of boundary horizontal maximum principal stress and extra stress, MPa;
σ—any arbitrary boundary horizontal stress, MPa;
σ°—any arbitrary reservoir horizontal stress, MPa;
σh—boundary horizontal minimum principal stress, MPa;
σH—boundary horizontal maximum principal stress, MPa;
Δσ—difference between boundary horizontal maximum and minimum stresses, MPa;
σ°h—reservoir horizontal minimum principal stress, MPa;
σ°H—reservoir horizontal maximum principal stress, MPa;
εm—deformation amount of mudstone, 10-3;
εs—deformation amount of sandstone, 10-3;
Δε—the deformation amount difference between mudstone and sandstone under the same stress conditions, 10-3;
θ—the angle between lithological interface and the direction of boundary horizontal maximum principal stress, (°).
Reference
Application of stratified stress method in massive hydraulic fracturing design
Effect of in-situ stress on hydraulic fracturing based on FDEM- Flow
Effect of crustal stress on hydraulic fracturing in coalbed methane wells
Optimization design method of well pattern based on in-situ stress field
Research on and application of large-scale fracturing technology in low porosity and ultra-low permeability laminated layers
Large-scale fluid-structure interaction simulation of viscoplastic and fracturing thin-shells subjected to shocks and detonations
Equipment outfitting and application for large-scale fracturing in shale gas horizontal wells
Difficulties and technical keys of fracturing reformation in shale gas reservoir
Finite element simulation of the present ground stress field of Sha-4 Member in the Chun-41 fault block
Study on the present ground stress of Es3 in Niu 35 fault block
Distribution of in-situ stress in oilfields
Some problems of in-situ crustal stress measurements
Research on reservoir rock mechanical parameters of Keshen foreland thrust belt in Tarim Basin
The experimental analysis of microstructure and mechanical properties of tight reservoir rocks
On the rock mechanics parameters anisotropy of sandstone
Statistical analysis of geostress distribution laws for difference rocks
Experimental study of relation between in-situ crustal stress and rock elastic modulus
Theoretical and experimental study of relation between in-situ stress and rock mass modulus
Influence of lithology and geologic structure on in situ stress: Examples of stress heterogeneity in reservoirs
Analysis of the influencing factors for ground stress in channel sandstone
Experimental study on effect of saturated water on rock mechanical properties
Experimental study on mechanical properties of grit stone after high temperature
Effect of confining pressure on the Young’s Modulus of rock specimen
Difference of lithofacies mechanical properties of the fourth member of Shahejie Formation in the Bonan Subsag, Bohai Bay Basin