Introduction
Permeability is an important parameter to characterize reservoir, and plays an important role in designing development plan and investigating underground fluid. It is of great significance to predict permeability[1]. At present, reservoir permeability prediction in petroleum industry is depending on logging data and core analysis. The analysis methods include mercury injection experiment and nuclear magnetic resonance (NMR). However, they are expensive and observation data of reservoirs are limited. Furthermore, these methods is difficult to be used to research the large-scale spatial distribution of reservoir permeability because these data are extracted from the well and do not contain lateral information. Seismic data has abundant information about lateral formation distribution. If we use seismic data to predict reservoir permeability, it can provide effective seepage field information for reservoir prediction, and it is of great significance to reservoir evaluation and development.
Reservoir permeability prediction by using seismic data has always been a frontier and difficult problem in reservoir prediction. Many scholars have conducted a lot of researches[2], using empirical method, seismic attribute analysis[3,4] and geostatistical simulation. Empirical method firstly make a linear regression between measured porosity and permeability and then apply the formula to actual seismic data. In the case of complex reservoir pores, it is always difficult to obtain the linear regression relationship between porosity and permeability, so the binary linear regression may bring a large error[2]. Seismic attribute analysis uses a neural network or other tools to establish a non-linear relationship between seismic attributes and permeability, and then transforms spatial seismic attributes into permeability volume[5]. This technique may lead to an over-fitting of the neural network when the number of samples is small. Geostatistical simulation uses the Co-kriging method to interpolate a permeability volume based on measured permeability as a primary variable and constrained by seismic attributes as secondary variables. This method requires abundant well data and uniform distribution of the logging locations[5].
In conclusion, there are still many difficulties in using seismic data to predict permeability. The primary reason is that the permeability is not only related to porosity but also affected by pore structure. Rocks with different pore structures differ widely in the correspondence between porosity and permeability. Considering pore structure in permeability prediction can reduce multiple solutions and improve prediction accuracy[6].
Previous studies have shown that elastic parameters can be used to predict pore structure, for example, pore aspect ratio[7] and frame flexibility factor[8], the two mainly pore structure parameters, can be calculated from elastic parameters. In recent years, Sun have proposed a new approach to predict permeability by combining porosity and frame flexibility factor, which has been successfully applied in carbonate reservoirs such as the Texas basins, USA and the Puguang gas field in the Sichuan Basin[8,9]. In this method, frame flexibility factor is calculated from logging data firstly, then the rock are classified according to the frame flexibility factor and observation of rock slices, finally the regression of porosity and permeability is carried out in each type of rock[8, 10-12]. By considering pore structure parameter, this technology effectively reduces the error in permeability prediction. But there are still many problems when it is applied in field data. Firstly, it is hard to classify rock by frame flexibility factor alone. It is necessary to comprehensively consider porosity and elastic parameters to improve the accuracy of lithofacies classification. Secondly, in this method, they obtain permeability from linear regression of porosity is too simple. Thirdly, permeability prediction only limited to logging data, how to apply in seismic data is uncertain. Lastly, the number of core slices are limited in the field data, so it is urgent to find another way to classify flexibility factor. In order to improve the effect of permeability prediction, a new permeability prediction method is proposed based on seismic and logging data. First, it uses porosity, elastic parameters and frame flexibility factor to analyze reservoir lithofacies, and then for each type of lithofacies, the permeability is obtained from multiply regression of porosity, elastic parameters and frame flexibility factor of the lithofacies. Applications have proved it effective in field data. This scheme provides a feasible idea for predicting spatial distribution of permeability. The method highlights the important roles of lithofacies and pore structure in permeability prediction. This is also the direction of complex reservoir prediction at present.
1. Method and principle
The methods used in this paper mainly involve in calculating frame flexibility factors, lithofacies classification and multiple regression. Since the multiple regression method is common, we only introduce how to calculate frame flexibility factors and lithofacies classification based on boosting learning (Adaboost).
1.1. Frame flexibility factors
Frame flexibility factors are parameters introduced into the new rock physical model derived by Sun, which include bulk frame flexibility factor ($\gamma $) and shear frame flexibility factor (${{\gamma }_{\mu }}$)[13]. These frame flexibility factors are used to describe the influence of shapes and sizes of pores on rock elastic properties. The bulk frame flexibility factor represents the volume strain under stress, and the shear frame flexibility factor represents shear deformation[11]. The formulas are as follows:
In general, fluid has a great influence on bulk modulus, which makes it difficult to calculate actual bulk frame modulus, but shear modulus is not affected. In this case, the shear modulus of dry rock can be approximately equivalent to the overall shear modulus of the rock, that is, $\mu ={{\mu }_{\text{d}}}$. Studies have shown that, in an area with low porosity, the difference of P-wave velocity of different pore types is relatively small, and shear flexibility factor has a more obvious response to the change of pore shape[11]. Therefore, shear flexibility factor is used in this study. Based on the above formulas, the formula for calculating shear flexibility factor can be obtained:
In this formula, the porosity can be calculated from density or total porosity, and the matrix shear modulus can be obtained from core analysis in laboratory. Generally, the velocities of P-wave and S-wave and the density of rock can be obtained by prestack seismic inversion, the porosity can be obtained by rock physical property constrained inversion or seismic attribute prediction, and by substituting them into the above formula, the shear flexibility factor can be calculated.
1.2. Lithofacies classification
Lithofacies classification is a basic work in well logging interpretation. It is time-consuming in manual interpretation. Using a machine learning method to classify lithofacies has become important. At present, the SVM lithofacies classification method is widely used, its main idea is to find a hyperplane to distinguish data. However, because the field data is very complex, it is difficult to classify lithofacies accurately by using SVM alone. Hence, the boosting learning algorithm (Adaboost) was used for lithofacies classification in this study.
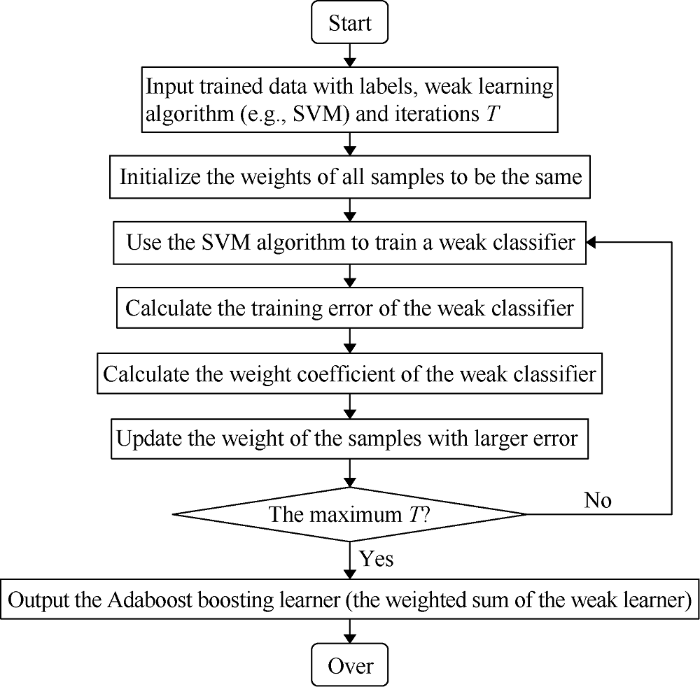
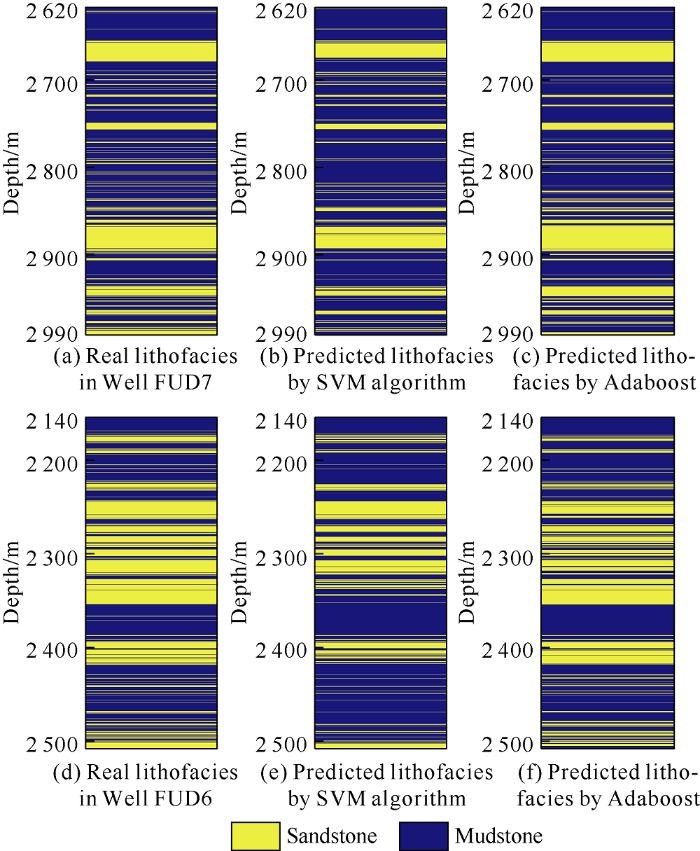
The boosting learning algorithm is an adaptive weight updating algorithm. In this method, some basic classifiers are trained firstly, and then the trained samples are given weights. Each time a new classifier is trained, the weight of trained samples is changed by using the new classifier, so the weight of correctly classified samples is reduced and the weight of incorrectly classified samples is increased, and the classifier model would pay more attention to the incorrectly classified samples, where cyclic iteration can effectively improve the classification effect of the general classifier. The specific algorithm flow is shown in Fig. 1[14]. In order to demonstrate the application of this method, we used the data of Well FUD7 and Well FUD6 to carry out lithofacies classification, and compared the classification result with SVM (Fig. 2). There are two types of lithofacies in Fig. 2, sandstone (yellow) and mudstone (blue). The comparison shows the classification accuracy of Adaboost (92.18% for Well FUD7 and 89.43% for Well FUD6) is higher than that of SVM (70.78% for Well FUD7 and 64.63% for Well FUD6).
Fig. 1.
Fig. 1.
Flow chart of boosting learning algorithm.
Fig. 2.
Fig. 2.
Comparison of lithofacies classification results by SVM and Adaboost of Well FuD7 (training data) and Well FUD6 (test data) in study area.
2. Permeability prediction based on logging data
2.1. Overview of the study area and reservoir geophysical characteristics
The study area is located at the Fudong slope in the east of the central depression of the Junggar Basin. The reservoir is mainly lithologic-stratigraphic ones. The Jurassic is divided into Badaowan Formation (J1b), Sangonghe Formation (J1s), Toutunhe Formation (J2t) and Qigu Formation (J3q) from bottom up. The bottom of the Toutunhe Formation uplifts and pinches out toward east, and contacts unconformably with the overlying Cretaceous conglomerate. The exploration target is the Toutunhe Formation, which is regressive deposits in river and delta. It is composed of gray, grey-green and brown, moderately thick and fine sandstone and siltstone interbedded with brown and light purple moderately thick mudstone. The sandstone has a porosity of 3.00%-30.25%, 16.65% on average, and a permeability of (0.017-696.610)×10-3 μm2, 4.13×10-3 μm2 on average.
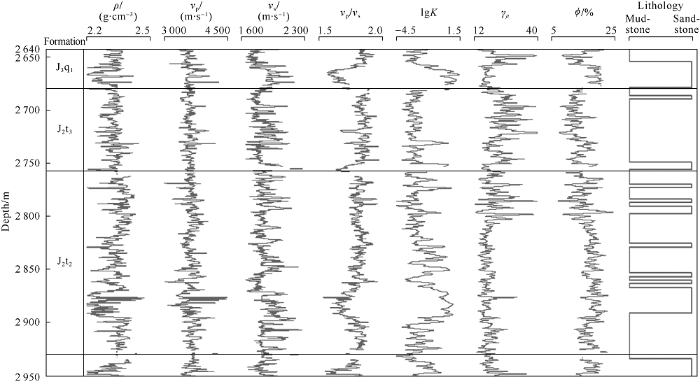
Fig. 3 shows the logging curves of Well FUD7. Petrophysical analysis shows that the P-wave velocity and density of the sandstone is less different from the mudstone in the Toutunhe Formation, the overlap of their acoustic impedance is serious, and it is difficult to distinguish them on the section of post-stack seismic inversion, but the VP/VS ratio has significant differences. Compared with tight dry sandstone, high-porosity sandstone shows low acoustic impedance and low VP/VS ratio. According to the logging curves in Fig. 3, the relationship between porosity and permeability is not obvious, but permeability and shear flexibility factor has a relationship. High permeability corresponds to low shear flexibility factor, but low shear flexibility factor may not means high permeability.
Fig. 3.
Fig. 3.
Logging curves of the upper Tunhe Formation in Well FUD7.
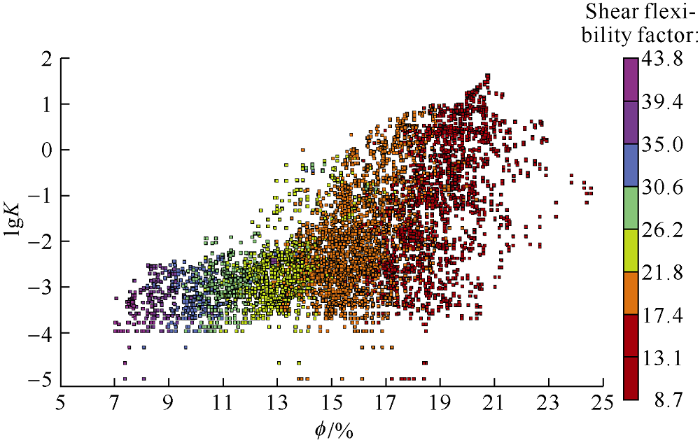
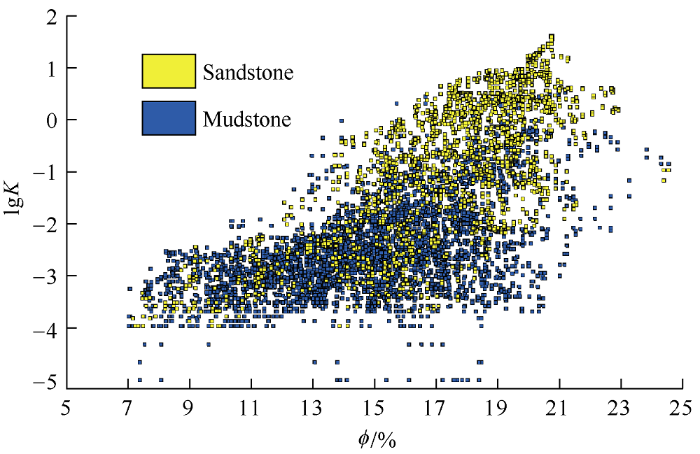
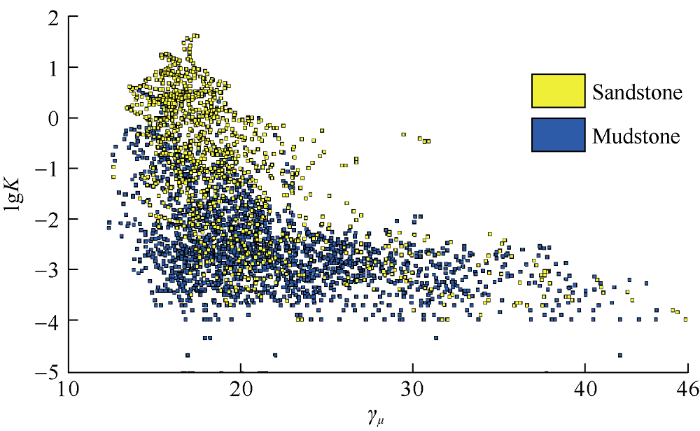
According to the prediction of logging permeability based on the flexibility factor proposed by Huang et al.[11], the relationship between flexibility factor and pore structure of rock slice is built, and then the zones are divided according to the hard threshold of the flexibility factor. Finally, the porosity-permeability relationship is fitted in each zone. Taking Well FUD7 as an example, we analyzed the feasibility of this method using the crossplot of porosity, permeability and flexibility factor. Fig. 4 is the crossplot of porosity, permeability and shear flexibility factor of the upper Toutunhe Formation in Well FuD7. Because no core slices are available from the corresponding well section, the flexibility is simply divided into eight sections. It can be found that one porosity value may correspond to permeabilities of different magnitudes, and the porosity and permeability have no obvious linear relationship. The shear flexibility factor may be effective, but not obvious enough to build the relationship between porosity and permeability. It is difficult to realize zone division by using hard threshold. From the crossplot of porosity-permeability-lithology of the well (Fig. 5), it can be found that different lithofacies overlap in the distribution range of permeability and porosity. From the crossplot of shear flexibility factor-permeability-lithology (Fig. 6), it can be found that different lithofacies overlap in flexibility and permeability. If lithofacies are not distinguished, it is difficult to effectively determine the relationship between flexibility factor and permeability. Therefore, it is difficult to predict permeability only by using porosity-permeability regression or empirical relationship between porosity and permeability after zone division based on flexibility factor. Since reservoir lithofacies have great influences on the relationship between porosity, permeability and shear flexibility factor, a new permeability prediction method combining shear flexibility factor with lithofacies was adopted in this study.
Fig. 4.
Fig. 4.
Crossplot of porosity-permeability-shear flexibility factor of the upper Toutunhe Formation in Well FUD7.
Fig. 5.
Fig. 5.
Crossplot of porosity-permeability-lithology of the upper Toutunhe Formation in Well FUD7.
Fig. 6.
Fig. 6.
Crossplot of shear flexibility factor-permeability-lithology of the upper Toutunhe Formation in Well FUD7.
2.2. Multi-factor regression based on shear flexibility factor
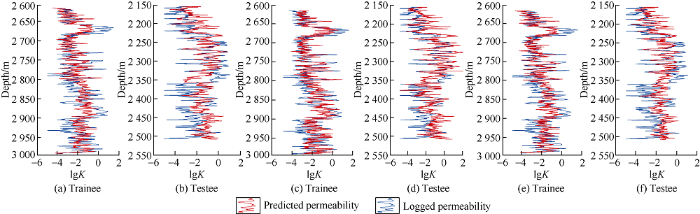
The above analysis shows that the correlation between permeability and porosity is poor, so we introduced other elastic parameters to improve the linear regression between them, and discussed the influence of flexibility factor on permeability prediction. In order to use seismic data, P-wave velocity, Vp/VS ratio, shear flexibility factor and porosity were taken to predict permeability (density was not considered here because of its low reliability), and the following tests were made: (1) to regress permeability based on porosity; (2) first to regress permeability based on porosity and shear flexibility factor, and then replace shear flexibility factor by P-wave velocity and Vp/VS ratio in turn, to analyze the influence of shear flexibility factor on permeability; (3) to predict permeability by porosity, P-wave velocity and Vp/VS ratio; (4) to regress permeability by porosity, P-wave velocity, Vp/VS ratio and shear flexibility factor (taking Well FUD7 as a train set and Well FUD6 as a test set). Table 1 shows the mean square error (MSE) and determination coefficient (R2) of the above multi-factor regressions. At here, the determination coefficient is the square of the related coefficient. The larger the determination coefficient represents the higher the correlation between the predicted results and real results. It can be seen that the permeability predicted by using porosity alone has larger error, and the prediction accuracy is improved by adding P-wave velocity, Vp/VS ratio and shear flexibility factor. But the combination of shear flexibility factor and porosity can improve the prediction accuracy of permeability more obviously (with a prediction error of 0.7765 after adding shear flexibility factor, which is smaller than the results of other methods). If porosity, P-wave velocity, Vp/VS ratio and shear flexibility factor are used for multi-factor regression, the prediction error is the lowest (0.7421). From the above analysis, it can be concluded that the multi-factor regression of elastic parameters and shear flexibility factors can improve the prediction accuracy of permeability. Compared with conventional elastic parameters such as P-wave velocity and Vp/VS ratio, shear flexibility factor is more sensitive to permeability and has greater significance in improving the prediction accuracy of permeability. Fig. 7 shows the comparison of permeability of Toutunhe Formation in Well FUD7 and Well FUD6 predicted by the above methods and the true permeability. Fig. 7a-7b are the permeability predicted by porosity only. Fig. 7c-7d are the permeability predicted by the combination of porosity and shear flexibility factor. Fig. 7e-7f are the permeability predicted by the combination of porosity, P-wave velocity, Vp/VS ratio and shear flexibility factor.
Table 1 MSEs and determination coefficients from multi-factor regression.
| Parameters | Facies classification | Well FUD7 | Well FUD6 | ||
|---|---|---|---|---|---|
| MSE | R2 | MSE | R2 | ||
| Porosity | No | 0.959 9 | 0.439 2 | 1.505 6 | 0.326 9 |
| Yes | 0.938 7 | 0.506 7 | 1.296 1 | 0.525 0 | |
| Porosity, P-wave velocity | No | 0.956 9 | 0.440 9 | 1.402 6 | 0.350 8 |
| Porosity, Vp/VS ratio | No | 0.923 9 | 0.460 2 | 1.401 4 | 0.392 1 |
| Porosity, Shear flexibility factor | No | 0.776 5 | 0.546 3 | 1.356 4 | 0.496 1 |
| Porosity, P-wave velocity, Vp/VS ratio | No | 0.897 5 | 0.475 7 | 1.075 6 | 0.498 9 |
| Yes | 0.892 4 | 0.540 8 | 0.954 2 | 0.592 5 | |
| Porosity, P-wave velocity, Vp/VS ratio, Shear flexibility factor | No | 0.742 1 | 0.566 4 | 0.935 6 | 0.601 6 |
| Yes | 0.672 1 | 0.794 8 | 0.894 3 | 0.792 4 | |
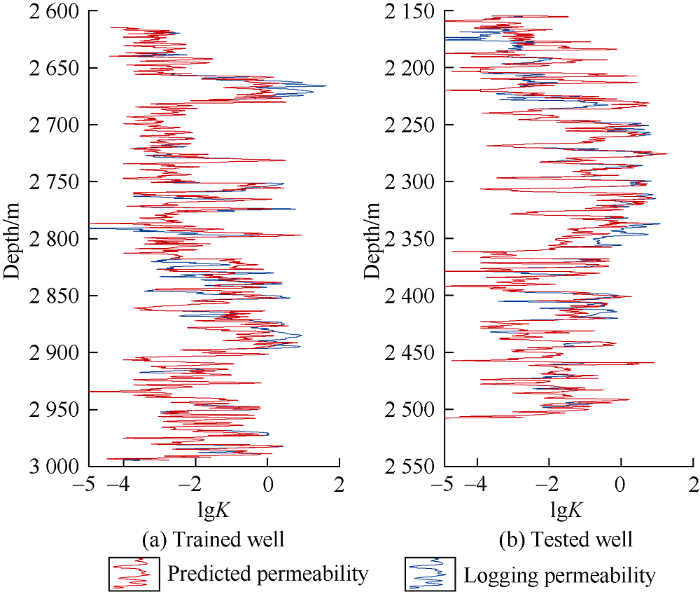
Fig. 7.
Fig. 7.
Permeability prediction results of the trainee (Well FUD7 well) and the testee (Well FUD6). (a), (b): only by porosity; (c), (d): by porosity and shear flexibility factor; (e), (f): by porosity, P-wave velocity, Vp/VS ratio and shear flexibility factor.
Further analysis of Fig. 7 shows that the prediction results still have large errors in some areas. After analyzing the lithofacies in the error section, it is found that the error mainly occurs in the mudstone section (2320-2350 m in Well FUD6), where the permeability is low, but the shear flexibility factor overlaps with the sandstone section, which is the main reason for the error. Therefore, the influence of lithofacies should be considered during permeability prediction.
2.3. Facies-controlling multi-factor regression based on shear flexibility factor
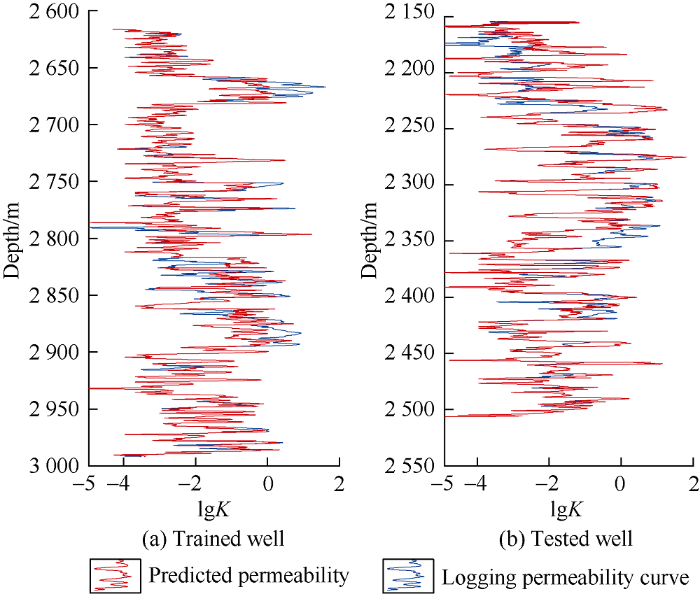
On the basis of the above experiments, we analyzed the influence of lithofacies on permeability prediction. In order to avoid the influence of lithofacies prediction error, real lithofacies obtained from mud logging was used firstly. Well FUD7 was a trainee and Well FUD6 was used for prediction. The specific steps were as follows: to calculate the regression relationship of different lithofacies in Well FUD7, and then apply the regression relationship to Well FUD6 to obtain the permeability. Fig. 8 shows the comparison between permeability predicted by facies-controlling regression and logging permeability. Fig. 9 shows the comparison between logging permeability and the permeability predicted by facies-controlling regression based on porosity, P-wave velocity and VP/VS ratio. Fig. 10 shows the comparison between logging permeability and the permeability predicted by facies-controlling regression based on porosity, P-wave velocity, VP/VS ratio and shear flexibility factor. The mean square errors and determination coefficients of the permeabilities predicted by the above facies-controlling prediction of permeability are shown in Table 1. Compared with the above multi-factor prediction error regardless of facies, the prediction errors before and after facies constrained are smaller, and the determination coefficient is larger. Moreover, when regression parameters include shear flexibility factor, the reduction of prediction error and the increase of correlation coefficient are the largest, that is, under the constrained by lithofacies, the multi-factor regression including elastic parameters and shear flexibility factor is a feasible scheme for reservoir permeability prediction.
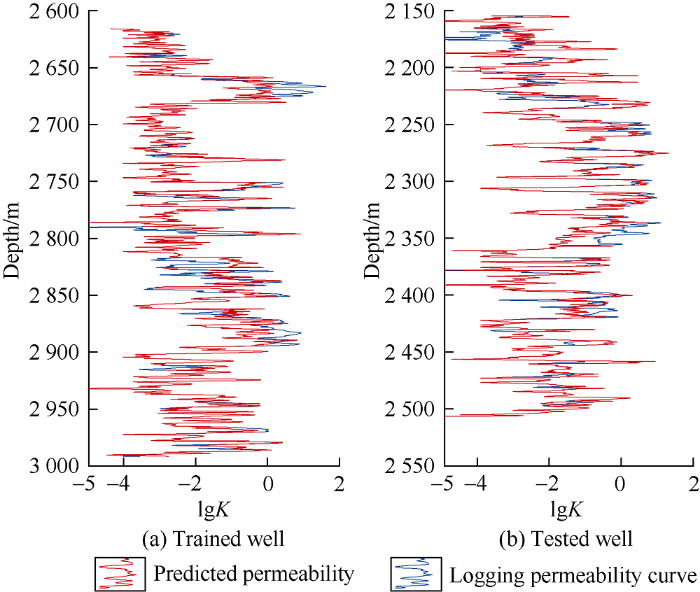
Fig. 8.
Fig. 8.
Comparison of permeability obtained by facies-controlling regression with logged permeability in the trained well (Well FUD7) and the tested well (Well FUD6).
Fig. 9.
Fig. 9.
Comparison of permeability obtained by porosity, P- wave velocity and VP/VS ratio regression with logging permeability of the trained well (Well FUD7) and the tested well (Well FUD6).
Fig. 10.
Fig. 10.
Comparison of permeability obtained by regression of porosity, P-wave velocity, VP/VS ratio and shear flexibility factor with logging permeability of the trained well (Well FUD7) and the tested well (Well FUD6).
Real lithofacies were used in the above analysis. The lithofacies can only be classified by known elastic data in actual application. In order to evaluate the influence of lithofacies classification error on permeability prediction, we designed three parameter combinations as follows: (1) porosity; (2) porosity + P-wave velocity + VP/VS ratio; (3) porosity + P-wave velocity + VP/VS ratio + shear flexibility factor. Based on the three parameter combinations, the lithofacies were classified by using SVM, and on this basis, the facies-controlling multi-factor regressions were carried out by using the respective parameter combinations. Well FUD7 was also taken as a trained well and Well FUD6 as a tested well. Table 2 shows comparison of errors between the permeability predicted based on logging lithofacies classification and that based on conventional lithofacies classification (SVM). It shows that conventional elastic parameters can be used to classify lithofacies but shear frame flexibility factor has little effect on the accuracy of lithofacies classification. It is remarkable that the lithofacies classification result has a great influence on permeability prediction. From the errors of predicted permeability, it can be found that the lithofacies classification obtained by SVM method is low in precision (about 70%). At this time, no matter adding conventional elastic parameters or shear flexibility factors for training and prediction, the error of permeability prediction is improved very little (Table 2), that is, the accuracy of lithofacies classification has a great influence on that of permeability prediction. Comparing the prediction results based on SVM in Table 2 with those without lithofacies classification in Table 1, we can see that the error of the former prediction is even greater than that of the later with lithofacies classification -- the prediction error without lithofacies classification is 0.9356, and that of SVM is 2.0627 for Well FUD6. Therefore, reliable lithofacies classification is the basis of accurate permeability prediction. Adding elastic parameters such as P-wave velocity and S-wave velocity can improve the accuracy of lithofacies classification. On the basis of accurate lithofacies classification, adding conventional elastic parameters such as P-wave velocity and VP/VS ratio can improve the accuracy of facies-controlling permeability prediction, but the effect is not as obvious as that by adding shear flexibility factor.
Table 2 Effect of lithofacies classification accuracy on facies-constrained permeability prediction.
| Parameters | Prediction method | MSE | Prediction method | Well FUD7 | Well FUD6 | |||
|---|---|---|---|---|---|---|---|---|
| Well FUD7 | Well FUD6 | Accuracy of facies classification | MSE | Accuracy of facies classification | MSE | |||
| Porosity | Conventional lithofacies identification | 0.938 7 | 1.296 14 | SVM | 0.703 3 | 0.958 7 | 0.482 3 | 2.488 0 |
| Porosity, P-wave velocity and Vp/VS ratio | 0.892 4 | 0.954 2 | 0.698 5 | 0.958 8 | 0.513 2 | 2.468 5 | ||
| Porosity, P-wave velocity, Vp/VS ratio and flexibility | 0.672 1 | 0.894 3 | 0.707 8 | 0.958 7 | 0.646 3 | 2.062 7 | ||
3. Prediction of permeability with seismic data
3.1. Prediction process
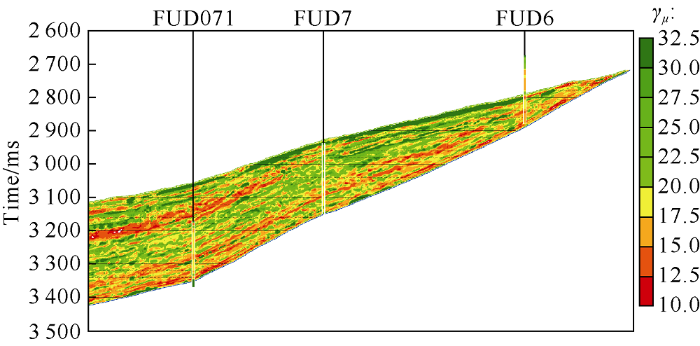
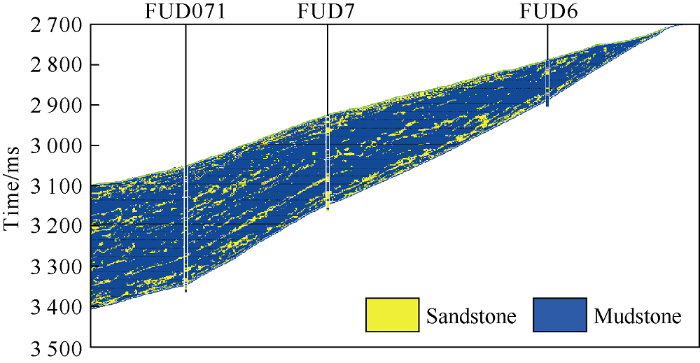
Through the above analysis, we came up with the scheme of permeability prediction by using seismic data. First, calculate porosity and shear flexibility factor through pre-stack seismic inversion, then use the pre-stack inversion result, porosity, shear flexibility factor to classify reservoir lithofacies, finally, based on the classification, the above attributes are used to carry out multi-factor regression to predict permeability. Fig. 11 shows the cross-well profile of calculated shear flexibility factor, Fig. 12 shows the lithofacies classification profile, and Fig. 13 shows the cross-well profile of logarithmic permeability.
Fig. 11.
Fig. 11.
Cross-well profile of shear flexibility factor of lower section of Toutunhe Formation in the study area.
Fig. 12.
Fig. 12.
Cross-well profile of lithofacies classification of lower section of Toutunhe Formation in the study area.
3.2. Analysis of prediction results
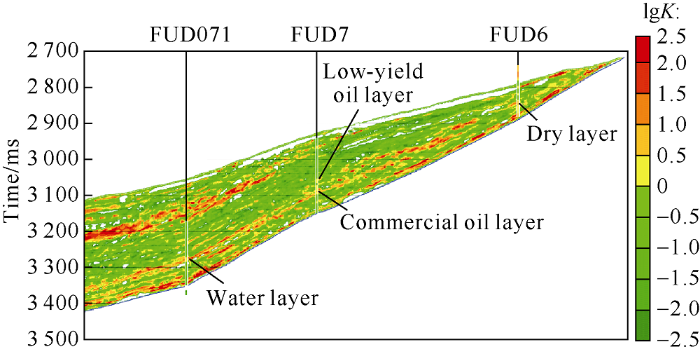
In order to verify the validity of the above prediction method, we still took Well FUD7 as a train set and Well FUD071 and Well FUD6 as tested data. According to the profile and embedded logging permeability, the logarithmic permeability coincides well (Fig. 13). The prediction error is within two color codes, that is, the permeability prediction error can be controlled within one order of magnitude.
Fig. 13.
Fig. 13.
Cross-well profile of logarithmic permeability of lower section of Toutunhe Formation in the study area.
On Fig. 13, the oil layer in Well FUD7 and the water layer of Well FUD071 have high porosity and good permeability, and the sandstone beds between the two wells are connected. Well FUD071 is in a lower structural position, so the sandstone produces water, while in Well FUD7 at higher structural position, the sandstone produces oil. In addition, the sandstone gradually thins toward structurally higher position in the east and pinches out between Well FUD7 and Well FUD6, so the dry layer in Well FUD6 and the oil layer in Well FUD7 are sandstone deposited at different stages. The sandstone of the low-yield oil layer in Well FUD7 has good physical properties, but thin and limited in distribution scope, so its production is low.
4. Conclusions
Permeability prediction based on logging data shows that shear frame flexibility factor characterizing pore structure, is more sensitive to permeability than conventional elastic parameters, and can be used for permeability prediction. In addition, the accuracy of lithofacies classification has a great influence on the accuracy of permeability prediction, and is the basis of accurate permeability prediction. The facies-controlling permeability prediction method based on shear frame flexibility factor can reduce the prediction accuracy in one order of magnitude. It provides an effective method for spatial permeability prediction using seismic data. In the future, we need to improve the lithofacies classification method and pore structure parameters estimation method to enhance the precision of permeability prediction.
Nomenclature
MSE—mean square error, dimensionless;
K—permeability, 10-3 μm2;
Kd—bulk modulus of dry rock, GPa;
Ks—matrix bulk modulus, GPa;
vp—P-wave velocity, m/s;
vs—S-wave velocity, m/s;
p—bulk modulus, GPa;
R2—determination coefficient, dimensionless;
T—number of iterations, dimensionless;
ρ—density, g/cm3;
γ—bulk frame flexibility factor, dimensionless;
γμ—shear frame flexibility factor, dimensionless;
ϕ—porosity, %;
μ—shear modulus, GPa;
μd—elastic modulus of dry rock, GPa;
μs—matrix elastic modulus, GPa.
Reference
Estimation of the permeability of hydrocarbon reservoir samples using induced polarization and nuclear magnetic resonance methods
Discussion on prediction permeability of seismic data
Application of seismic porosity inversion techniques to sandstone reservoirs in western Sichuan Basin and its effect comparison
Rock skeleton models and seismic porosity inversion
Permeability prediction by seismic attribute data
Seismic prediction method of permeability of reef bank reservoir with complex pore types in Puguang gas field
Inversion of effective pore aspect ratio for shale reservoir using grid search method
Rock-physics-based carbonate pore type characterization and reservoir permeability heterogeneity evaluation, Upper San Andres reservoir, Permian Basin, west Texas
Preliminary application of the frame flexibility factor in Puguang gas field
Rock-physics-model-based pore type characterization and its implication for porosity and permeability qualification in a deeply-buried carbonate reservoir, Changxing Formation, Lower Permian, Sichuan Bain, China
Characterization of pore structure variation and permeability heterogeneity in carbonate rocks using MICP and sonic logs: Puguang gas field, China
Effects of pore structure on 4D seismic signals in carbonate reservoirs
Pore structure effects on elastic wave propagation in rocks: AVO modelling
Porosity and permeability prediction from wireline logs using artificial neural networks: A North Sea case study