Introduction
“Tight reservoirs”, with rich oil and gas resource, are generally tight, but strong in heterogeneity still. Tight reservoirs in different areas differ widely in moveable fluid content[1,2,3]. Pore structure not only determines the storage and flow characteristics of these reservoirs, but also their fracturing effects and ultimate recoverable reserves[3,4]. Therefore, pore structure and controlling factors of reservoir quality are important for the exploration and development of tight oil.
Pores in tight reservoirs are mostly nano and micron scale, mostly less than 2 μm[5,6]. For example, the pores in Triassic Yanchang Formation of Ordos Basin are largely 50-900 nm in size[7]. Since pores of different types vary widely in size, pore size of tight reservoirs may be continuous, unimodal, or bimodal[4,7-9]. In tight sandstone, large pores often determine the permeability, while small pores contribute the most part of pore volume[9,10,11,12,13], pore-throats of different orders have different effects on porosity and permeability. But which order of the pore-throat has the major influence on tight sandstone poro-permeability, and how pore size distribution is related to oil occurrence in tight sandstones are rarely discussed.
Usually each testing method characterizes the pore structure based on a single pore model. For example, capillary model is used to represent the pore throat structure during mercury intrusion testing, which is inefficient to reflect the structural diversity of pore throat with different size. Fractal geometries are widely used to describe pore structure in recent years, however different conclusions are exist in recent works. For example, in many works the fractal dimension of small pores show a negative correlation with permeability of sandstone, indicating that small pores controls the complexity of pore systems. The more complicated the small pore structure, the lower the permeability[14,15]. Some other works had opposite conclusion that macro pores had more important influence on the pore structure as they had larger fractal dimension[16]. The main cause for these opposite conclusions is that the fractal dimension of pore space is calculated based on a single and simplified pore model which is unable to describe the pore structure variation with pore size.
In this work, the fractal dimension of pore throat of typical tight sandstone samples from Chang 7 member, Yanchang Formation, Ordos Basin, are calculated by mercury intrusion data. The structure of pore throat with different sizes and its differential controls on reservoir quality and oil saturation are further analyzed based on thin sections, porosity, permeability, oil saturation data.
1. Samples and methods
1.1. Samples and testing methods
14 core samples of Chang7 tight sandstone from Ordos Basin were selected for thin section petrology, porosity, permeability and mercury intrusion tests (Tables 1 and 2). Fractal dimension of each sample was calculated with the mercury intrusion test data. To find out the effect of pore structure on oil saturation, the sandstone samples with oil and gas shows were taken preferentially.
Table 1 Petrologic features of tight sandstone samples.
| No. | Well | Depth/ m | Quartz/% | Feldspar/% | Rock fragment/% | Mica/ % | Other debris/ % | Matrix/% | Authigenic mineral/% | Thin section porosity/% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Igne- ous rock | Quart- zite | Phyl- lite | Other metamor- phic rock | Sedi- mentary rock | Chlo- rite | Ferro calcite | Anke- rite | Silica | Other | Inter- granular pore | Particle dissolution pore | Total | ||||||||
| 1 | B279 | 1 915.2 | 40.5 | 9.2 | 2.0 | 1.8 | 7.8 | 4.5 | 3.7 | 17.2 | 0.8 | 7.8 | 0 | 0.5 | 4.0 | 0.2 | 0 | 0.1 | 0.4 | 0.5 |
| 2 | Z62 | 1 853.8 | 26.0 | 46.0 | 3.0 | 1.0 | 1.5 | 0 | 3.5 | 3.0 | 4.5 | 5.0 | 0 | 2.0 | 0 | 0.5 | 4.00 | 0 | 0.3 | 0.3 |
| 3 | B502 | 1 956.7 | 31.5 | 38.0 | 0.7 | 0 | 5.0 | 2.0 | 4.7 | 9.0 | 1.0 | 4.8 | 0 | 2.5 | 0.5 | 0.3 | 0.80 | 0 | 0.3 | 0.3 |
| 4 | N28 | 1 702.4 | 36.0 | 27.0 | 2.5 | 2.0 | 3.0 | 2.0 | 7.0 | 5.0 | 1.0 | 8.0 | 2 | 3.0 | 0.5 | 1.0 | 0 | 0 | 0.7 | 0.7 |
| 5 | N46 | 1 641.6 | 35.5 | 7.5 | 0.7 | 0 | 5.0 | 2.0 | 4.7 | 9.5 | 0 | 31.8 | 0 | 2.5 | 0.5 | 0.3 | 0.80 | 0 | 0.3 | 0.3 |
| 6 | L72 | 1 915.1 | 50.5 | 17.0 | 4.0 | 1.5 | 3.5 | 1.5 | 8.0 | 3.0 | 0 | 9.0 | 0 | 0 | 1.0 | 1.0 | 0 | 0 | 1.1 | 1.1 |
| 7 | Z211 | 1 580.1 | 43.0 | 27.5 | 3.5 | 2.0 | 1.5 | 1.5 | 4.5 | 2.5 | 0 | 8.5 | 1 | 0.5 | 2.0 | 1.5 | 0.50 | 0.2 | 0.6 | 0.8 |
| 8 | N34 | 1 600.4 | 47.0 | 20.0 | 4.5 | 1.0 | 3.0 | 2.0 | 2.5 | 4.0 | 0 | 15.0 | 0 | 1.0 | 0 | 0 | 0 | 0 | 0.4 | 0.4 |
| 9 | T2 | 1 669.9 | 24.5 | 43.5 | 3.0 | 1.0 | 2.0 | 1.0 | 4.5 | 6.5 | 1.0 | 7.0 | 0 | 3.0 | 1.0 | 2.0 | 0 | 0.1 | 0.2 | 0.3 |
| 10 | B269 | 1 969.3 | 22.5 | 41.0 | 4.0 | 1.5 | 4.0 | 1.0 | 4.0 | 5.0 | 0 | 12.0 | 0 | 4.0 | 0 | 1.0 | 0 | 0.2 | 0.5 | 0.7 |
| 11 | L19 | 1 765.4 | 50.0 | 12.0 | 5.0 | 3.0 | 2.5 | 1.5 | 13.0 | 2.0 | 2.0 | 3.0 | 1 | 0 | 1.0 | 1.0 | 3.00 | 1.5 | 0.5 | 2.0 |
| 12 | G56 | 1 953.0 | 23.0 | 48.0 | 4.0 | 2.0 | 3.0 | 2.0 | 1.1 | 6.0 | 1.2 | 4.0 | 0 | 4.5 | 0 | 1.2 | 0 | 1.0 | 1.3 | 2.3 |
| 13 | N18 | 1 672.0 | 45.0 | 28.0 | 3.0 | 2.0 | 1.0 | 0 | 6.0 | 4.0 | 5.0 | 2.0 | 0 | 2.0 | 0 | 2.0 | 0 | 1.0 | 0.6 | 1.6 |
| 14 | X233 | 1 973.8 | 54.0 | 18.5 | 3.0 | 4.0 | 1.5 | 1.5 | 4.5 | 4.5 | 0 | 3.5 | 0 | 0 | 2.0 | 2.0 | 1.00 | 0.4 | 3.3 | 3.7 |
Table 2 Mercury intrusion data of 14 samples.
| No. | Porosity/ % | Permeability/ 10-3 μm2 | Oil saturation/ % | Displacement pressure/MPa | Median pressure/MPa | Maximum connection radius/μm | Peak radius/μm | Maximum mercury saturation/% |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.0 | 0.0276 | 7.83 | 0.08 | 0.09 | 64.93 | ||
| 2 | 7.4 | 0.0840 | 30.84 | 4.48 | 29.67 | 0.16 | 0.09 | 60.30 |
| 3 | 8.3 | 0.0700 | 4.89 | 28.79 | 0.15 | 0.09 | 48.57 | |
| 4 | 8.4 | 0.0670 | 50.20 | 5.58 | 27.69 | 0.13 | 0.07 | 61.60 |
| 5 | 8.8 | 0.0891 | 38.79 | 7.89 | 45.73 | 0.09 | 0.07 | 50.60 |
| 6 | 9.0 | 0.0660 | 44.86 | 3.11 | 9.91 | 0.24 | 0.12 | 71.80 |
| 7 | 9.2 | 0.0570 | 41.99 | 3.92 | 11.23 | 0.19 | 0.08 | 76.00 |
| 8 | 9.7 | 0.0420 | 45.41 | 5.31 | 18.65 | 0.14 | 0.09 | 69.20 |
| 9 | 9.8 | 0.0500 | 31.12 | 5.77 | 14.91 | 0.13 | 0.09 | 75.20 |
| 10 | 10.2 | 0.1000 | 45.23 | 4.02 | 10.64 | 0.18 | 0.10 | 77.10 |
| 11 | 11.1 | 0.1250 | 41.70 | 2.58 | 6.78 | 0.11 | 0.15 | 84.93 |
| 12 | 11.7 | 0.2370 | 2.86 | 12.39 | 0.26 | 0.15 | 77.90 | |
| 13 | 12.5 | 0.2250 | 23.70 | 2.27 | 9.30 | 0.33 | 0.18 | 81.23 |
| 14 | 13.8 | 0.2820 | 72.31 | 1.41 | 3.78 | 0.52 | 0.25 | 75.00 |
Plug samples 2.5 cm in diameter were drilled from the core to make cast thin section and to be used in physical property and mercury intrusion tests. Before testing, the core plug was washed to remove crude oil and salt contamination, the sample was washed using a Soxhlet extractor with a solvent mixture of methanol and methylene chloride. Cleaning procedure was finished until the extract remained clear and showed no luminescence under fluorescent light. Then, the sample was dried in microwave at 100 °C for 24 h. Red resin was then injected into the dried sample for pore identification. Thin section 0.03 μm thick was made using finer abrasive grit. Texture, composition, and pores were observed and counted at 300 points per thin section under a polarizing petrographic microscope.
Porosity was measured by core helium porosimeter with air method. Permeability was measured by pressure-falloff gas permeameter with the permeability test range from 0.001× 10-3 μm2 to 30 000×10-3 μm2. Oil saturation data of 11 fresh cores with the same depth was collected in this work. High- pressure mercury intrusion testing was done on AutoPoreIV mercury porosimetry at 22 °C, relative humidity of 46%-68%, and the mercury interfacial tension (σ) of 0.49 N/m.
1.2. Pore throat structure parameter
Mercury is non-wetting phase for most solid interfaces and needs to overcome capillary pressure to get into the capillary. According to the Young-Laplace equation[17], mercury intrusion pressure pc is controlled by throat radius r, interfacial tension σ and contact angle θ:
The capillary pressure curve can be obtained based on mercury intrusion volume and the corresponding pressure to work out important parameters such as displacement pressure, and medium pressure (injection pressure when mercury saturation is 50%). Then, by using formula (1), pore structure parameters such as maximum interconnected radius, median radius and pore throat radius distribution curve can be calculated.
1.3. Fractal dimension calculation
Fractal is defined as "a rough or fragmentary geometry that can be divided into several parts, and each part of which has the same statistical character as the whole", namely the self-affinity nature. Fractal dimensions of the 14 samples were calculated with capillary pressure data in this work. According to the fractal theory, the number of the units N(r) has a power-law function with the radius r of the unit chosen to fill the fractal object[18]:
If reservoir pores have fractal feature, the radius of pore throat (r) is the measured linear scale. N(r) can be calculated with pore throat radius r and injected mercury volume VHg according to the capillary tube model:
Arranging Eqs. (1) and (2):
Substituting Young-Laplace Eq. (1) into Eq. (5):
Mercury saturation SHg can be expressed as:
Assuming that length l is constant, the relationship between SHg and pc can be obtained by substituting Eq. (6) into Eq. (7):
where α is a constant, mercury saturation SHg has a Power-law relationship with capillary pressure Pc. Taking logarithm on both sides of Eq. (8):
lg SHg -lg pc shows a linear relationship with intercept C on a log-log plot. Fractal dimension (D) can be calculated from the slope of linear relationship of lg SHg-lg pc.
2. Results
2.1. Petrologic features
Mineralogical data obtained by point-counting shows that the 14 samples include lithic feldspathic sandstone, lithic sandstone and feldspar lithic quartz sandstone. They have a quartz content range from 22.5%-54.0%, 38.6% on average, and feldspar content range from 7.5%-48.0%, 26.0% on average. In the samples, the lithic fragments are mainly metamorphic rock, quartzite, and phyllite, accounting for 9.0% to 25.0%, 14.5% on average; interstitial materials are mainly clay matrix dominated by hydro mica, accounting for 2.0% to 31.8%, 8.3% on average; cement accounts for 5.5% on average, and is mainly composed of ferrocalcite and ankerite (with a mean content of 1.6% and 1.0% respectively), followed by silica, minor clay and albite. The samples are mostly coarse siltstone, fine-grained sandstone and graywacke with grain size ranging from 0.08-0.30 mm, 0.16 mm on average. The clasts are moderately to poorly sorted and mostly subangular.
2.2. Pore types, porosity and permeability
Observation of thin sections shows the tight sandstone samples have many types of pores. Pores that are large in size and can be clearly identified under polarizing microscope include well-preserved intergranular pores and grain dissolution pores. These large pores were counted mainly in surface porosity statistics. In addition, these samples have some small pores, which are easy to identify because of the adsorbed asphalt, but are difficult to count their surface porosity. These small pores include: small residual pores resulting after intense compaction and cementation, small dissolution pores formed by weak dissolution, intercrystalline pores associated with clay minerals, such as illite, flake-like interlamellar micropores formed as a result of mica alteration and micropores within phyllite and schist metamorphic rock fragments (Fig. 1).
Fig. 1.
Types and characteristics of pores commonly seen in the samples.
The surface porosity of the 14 samples varies widely from 0.3% to 3.7%, with an average of 1.1%. The porosity of dissolution pores (mainly feldspar dissolution pores) and intergranular pores average at 0.8% and 0.3% respectively (Table 1). Physical property tests show the samples have a porosity range from 5.0% to 13.8%, 9.42% on average, and a permeability range from 0.027 6 to 0.282 0 (×10-3 μm2). The oil saturation of 11 fresh core samples taken from the same depth ranges from 23.7% to 72.3%, with an average of 42.3% (Table 2). The ratio of the pore volume with oil to the whole rock volume is defined as the oil-bearing porosity. Oil bearing porosity is the product of oil saturation and effective porosity. The calculated results show the oil-bearing porosity of the samples range from 2.3% to 10.0%, with an average of 4.26%.
2.3. Mercury intrusion
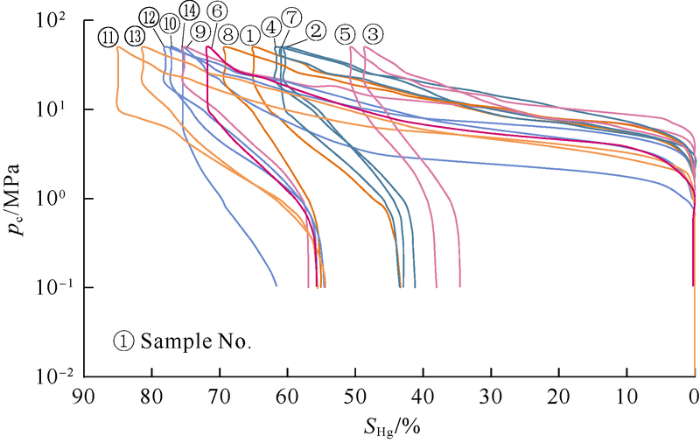
Capillary pressure curves of the 14 samples are shown in Fig. 2. It can be seen all the curves have small skewness and well sorting. But the samples vary widely in maximum mercury saturation from 48.47% to 84.93%, with an average of 69.6% (Table 2 and Fig. 2). A considerable part of pore throats (30%) are too small to have mercury injected. The samples have displacement pressures from 1.41 to 7.89 MPa, 4.42 MPa on average; medium pressure from 0 to 45.73MPa, 15.43 MPa on average; and maximum interconnected radius from 0.08 to 0.52 μm, 0.19 μm on average (Table 2).
Fig. 2.
Capillary pressure curves of the 14 samples.
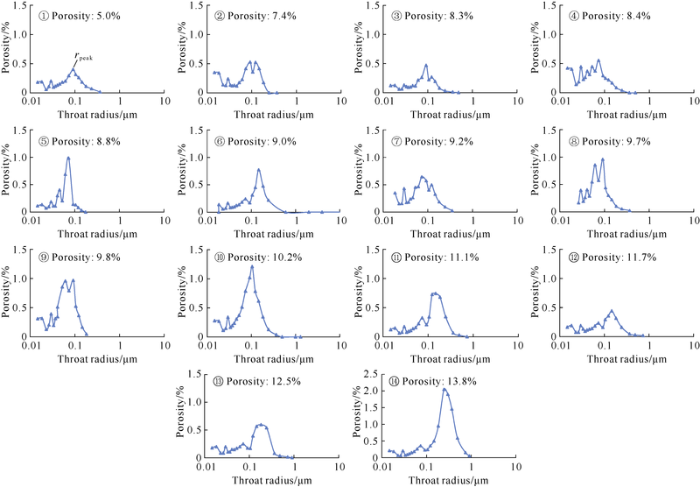
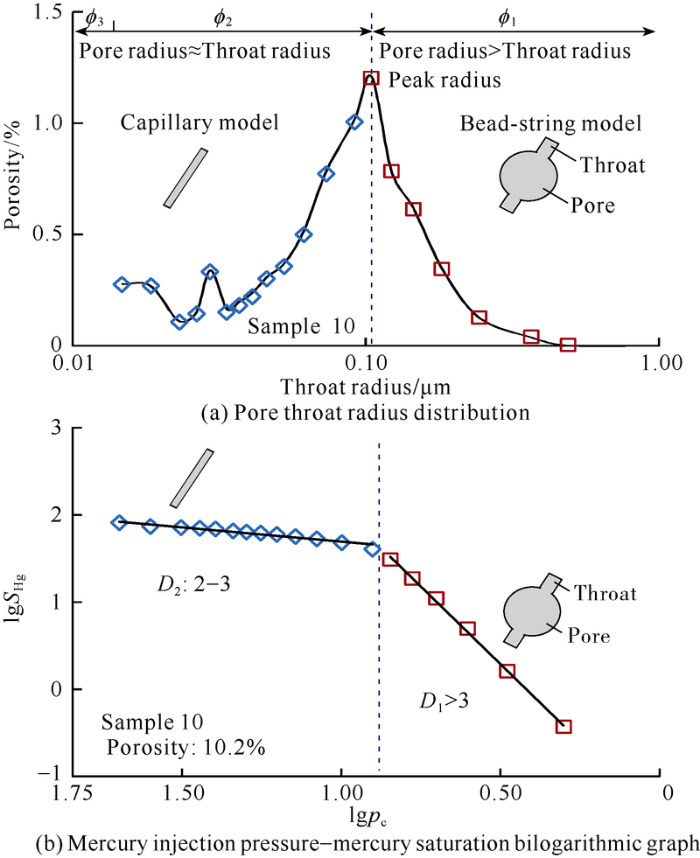
Pore throat radius distribution converted from Pc and VHg shows that the 14 samples all have pore throat radius of less than 1 μm (Fig. 3) and single peak in pore throat radius distribution. If peak radius is defined as the apex of radius distribution curve, the samples range from 0.07-0.25 μm in peak radius, with an average of 0.11 μm. Peak radius increases with the increase of porosity, for example, samples No.1-No.5 and No.7-No.9, with small porosity, have peak radius of less than 0.1 μm; while samples No.9-No.14 with porosity of more than 10% have peak radius of more than 0.1 μm.
Fig. 3.
Pore throat radius distribution of the tight sandstone samples.
2.4. Fractal dimensions
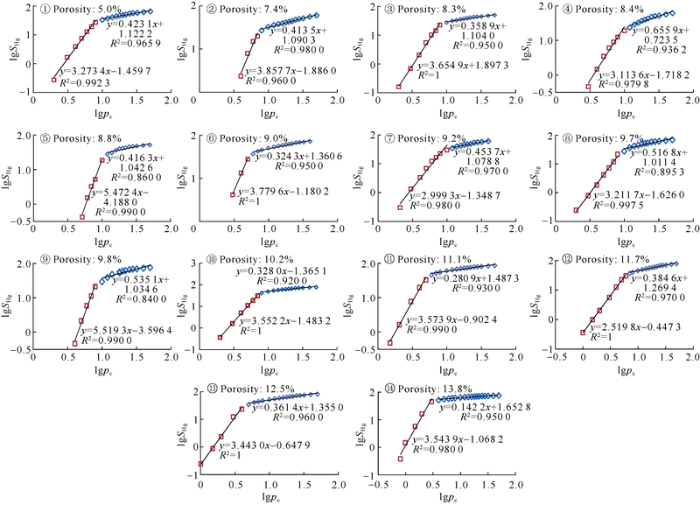
Fractal dimensions calculated from mercury intrusion data is presented in Table 3 and Fig. 4. Fig. 4 shows that the capillary pressure vs. injection mercury saturation curves of all samples in the log-log diagram have two distinct linear segments with different slopes. The first segment is characterized by low capillary pressure and high slope, representing the fractal characteristics of large pore throat. The second half segment therefore represents the fractal features of small pore throat. The correlation coefficients of both segments are generally greater than 0.90, except for second segment of sample No.5 and No.9 (which are 0.86 and 0.84) (Table 3).
Fig. 4.
Mercury injection pressure - mercury saturation bilogarithmic graph of the samples(R represents correlation coefficient).
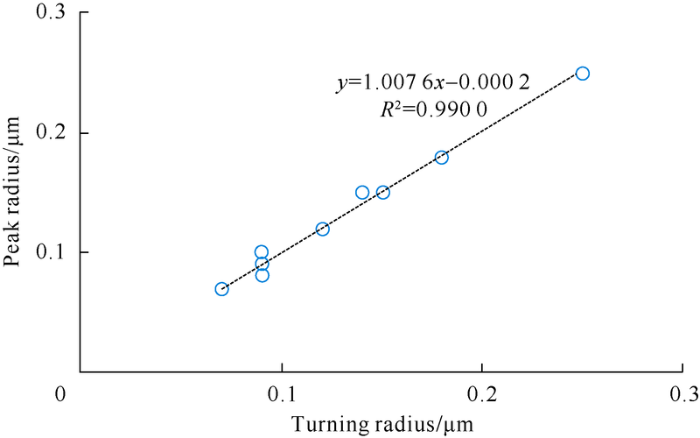
The pore throat radius corresponding to the turn point of the two segments is defined as turning radius. The turning radius is approximately equal to the peak radius, with a correlation coefficient of 0.99 (Table 3 and Fig. 5). Therefore, the turning radius is regarded as the peak radius. According to formula (9), fractal dimension D1 of large pore throat of the first segment of the samples were calculated, ranging from 4.52-7.52, on average 5.62; and the fractal dimension D2 of small pore throat of the samples range from 2.14-2.66, with an average of 2.40 (Table 3).
Table 3 Fractal dimensions and ϕ1, ϕ2 and ϕ3 of the 14 samples.
| No. | D1 | R1 | D2 | R2 | Turning radius/μm | ϕ1/% | ϕ2/% | ϕ3/% |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.27 | 0.97 | 2.42 | 0.970 | 0.09 | 1.35 | 1.90 | 1.75 |
| 2 | 5.46 | 0.95 | 2.41 | 0.980 | 0.09 | 1.46 | 3.01 | 2.94 |
| 3 | 5.65 | 0.99 | 2.36 | 0.953 | 0.09 | 1.85 | 2.18 | 4.27 |
| 4 | 5.11 | 0.98 | 2.66 | 0.940 | 0.07 | 1.60 | 3.58 | 3.23 |
| 5 | 7.47 | 0.99 | 2.42 | 0.860 | 0.07 | 1.61 | 2.84 | 4.35 |
| 6 | 5.27 | 0.98 | 2.34 | 0.950 | 0.12 | 2.51 | 3.95 | 2.54 |
| 7 | 5.23 | 0.99 | 2.50 | 0.960 | 0.09 | 2.10 | 3.50 | 2.21 |
| 8 | 5.21 | 1.00 | 2.52 | 0.900 | 0.09 | 2.10 | 4.61 | 2.99 |
| 9 | 7.52 | 0.99 | 2.54 | 0.840 | 0.09 | 2.06 | 5.31 | 2.43 |
| 10 | 5.45 | 1.00 | 2.28 | 0.950 | 0.09 | 4.14 | 3.72 | 2.34 |
| 11 | 5.57 | 0.99 | 2.28 | 0.940 | 0.15 | 3.62 | 5.81 | 1.67 |
| 12 | 4.52 | 1.00 | 2.39 | 0.970 | 0.14 | 3.53 | 5.59 | 2.58 |
| 13 | 5.44 | 1.00 | 2.36 | 0.960 | 0.18 | 2.90 | 7.31 | 2.29 |
| 14 | 5.54 | 0.98 | 2.14 | 0.950 | 0.25 | 6.19 | 4.22 | 3.45 |
Fig. 5.
Correlation between turning radius and peak radius.
3. Discussions
3.1. Effects of pore throats of different scales on porosity and permeability
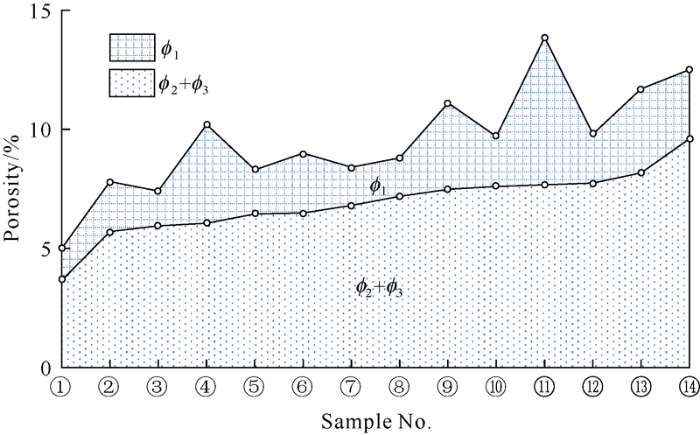
Supposing the pore throat larger than the peak radius is large pore throat with a porosity of ϕ1; the pore throat smaller than the peak radius allowing mercury injection is small pore throat, with a porosity of ϕ2, and the pore throat that mercury cannot be injected into under testing condition is micro pore throat, with a porosity of ϕ3 (Table 3). The 14 samples have an average ϕ1 of 2.64%, less than ϕ2 (4.11% on average) and ϕ3 (2.79% on average). The variation coefficient of ϕ1 is 0.51, which is larger than that of ϕ2 (0.37) and ϕ3 (0.29), indicating that: (1) For the 14 samples, small pore throats make the most contribution to pore volume, followed by micro pore-throats, and large pore throats. (2) The samples vary widely in development degree of large pore throat, but stable and similar small pore throats and micro-pore throats (Fig. 6).
Fig. 6.
Distribution of ϕ1 , ϕ2 and ϕ3 of the samples.
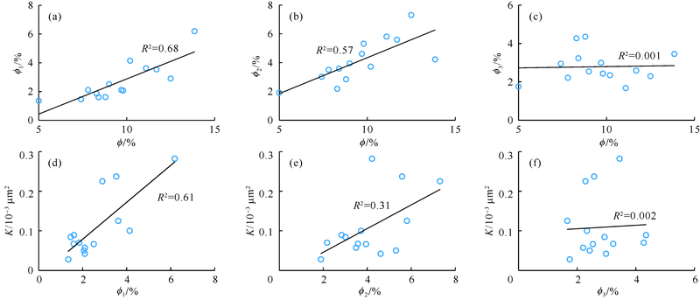
ϕ1 and ϕ2 are positively correlated with the porosity ϕ (Fig. 7), with correlation coefficients of 0.68 and 0.57, respectively. ϕ3 shows no correlation with ϕ. ϕ1 is positively correlated with permeability, with a correlation coefficient of 0.61, ϕ2 has poorer correlation with permeability, with a correlation coefficient of (0.31), and ϕ3 has no correlation with permeability. The correlations of ϕ1, ϕ2 and ϕ3 with porosity and permeability indicate that the large pore throat is the main controlling factor for the variations of porosity and permeability, despite its low contribution rate to pore volume, this is different from the previous understanding that the large pore throat only affects permeability[13,14,15]. The small pore throat contributes some to porosity variation, but has minor effect on permeability. Whereas the micro pore throat shows no influence on both porosity and permeability change. Therefore, it can be concluded that the large pore throat in tight sandstone is the major factor for the reservoir property heterogeneity.
Fig. 7.
Correlation between porosity, permeability and ϕ1, ϕ2 and ϕ3.
3.2. Effects of ϕ1, ϕ2 and ϕ3 on oil occurrence
It is generally believed that oil can be stored in pores with sizes from micron to several nanometers in tight oil reservoirs[19,20] and is moveable in pores more than 0.02 μm in diameter[21]. But this study shows oil bearing porosity only has moderate to good correlation with ϕ1 (R2: 0.76, Fig. 8) and no correlation with ϕ2 and ϕ3 (R2: 0.000 4 and 0.050 0 respectively). This indicates: (1) Large pore throat is critical for oil emplacement. During oil accumulation, oil would charge into large pore throats firstly, and then small and micro pore throats. If oil mainly filled in small pore th roats, oil bearing porosity should have been well correlated with ϕ2. Based on the ϕ1 of large pore throat and oil-bearing porosity of the samples, if the large pore throats are fully filled with oil, then about 65% of the oil phase on average will be stored in the large pore throats. (2) Pore throat size distribution of tight sandstone during the oil accumulation should be similar to present state. As long as the large pore throats were filled with oil, the oil saturation would probably remain unchanged, because when oil accumulated in Chang7 tight sandstone, the Chang7 sandstone had been deep buried and intensely compacted, and would be fairly stable thereafter; additionally, oil emplacement would prohibit the effects of cementation and compaction from reducing the porosity[22,23]. Therefore, after large scale oil charge, the pore throat feature of the Chang 7 tight sandstone should be stable. If the porosity changed obviously further after oil emplacement, for instance, many large pore throats reduced to small pore throats, then a large portion of oil should have occurred in small pore throats, and the contribution of small pore throats to oil bearing porosity should have increased, and the correlation of them should have turned better, and the correlation between oil-bearing porosity and large pore throat should have been poor. Therefore, in addition to controlling the porosity and permeability of tight sandstone, the development degree of large pore throat is also critical for oil emplacement, and is a key parameter for evaluating tight oil reservoirs.
3.3. Origins of different scales of pore throats
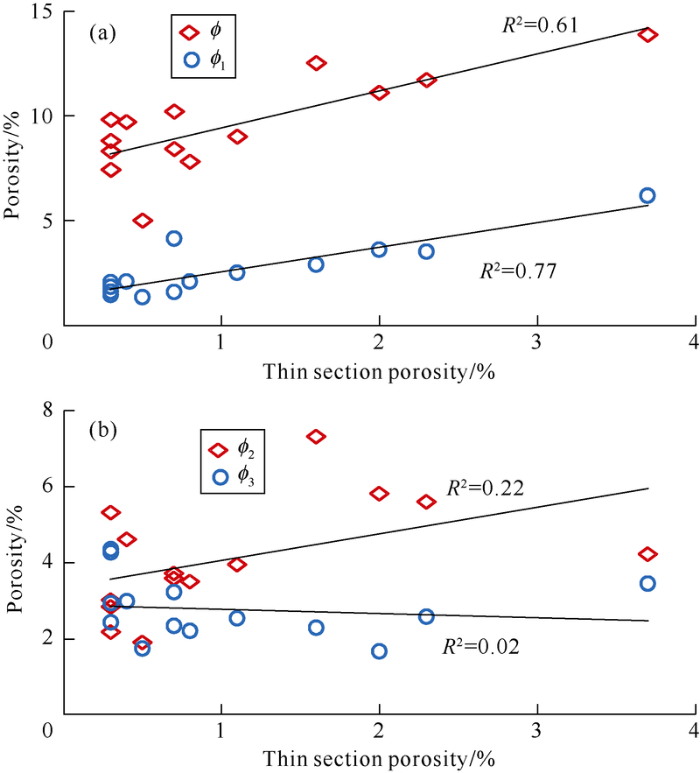
The 14 samples have a surface porosity range of 0.3% to 3.7% from thin section observation, which are obviously lower than their porosity range from core test, indicating that there are still many small and micro pores not be counted[24,25,26]. Thin section observation mainly reflects development situation of large pores, while small and micro pores are difficult to identify by this means[24]. Mercury intrusion experiment can only provide information of throat radius and pore volume connected by the throat but can’t reflect pore size distribution[5]. But thin section surface porosity is in good correlation with core porosity and large pore throat porosity ϕ1 (with R2 of 0.61 and 0.77 respectively)(Fig. 9), indicating that large throats in tight sandstone usually connect with large pores. Therefore, the large pore that can be identified and counted in thin section observation is the major factor controlling porosity, permeability and pore structure, which is consistent with the conclusion from NMR analysis in previous studies [16]. In terms of pore type, visible pores in the samples mainly include particle dissolution pores and intergranular pores, with average surface porosity of 0.8% and 0.3%, respectively. Therefore, the development of large pore is an important factor for reservoir quality evaluation and prediction.
Fig. 9.
Scatter plots of surface porosity versus ϕ,ϕ1, ϕ2 and ϕ3.
3.4. Binary pore structure of tight sandstone
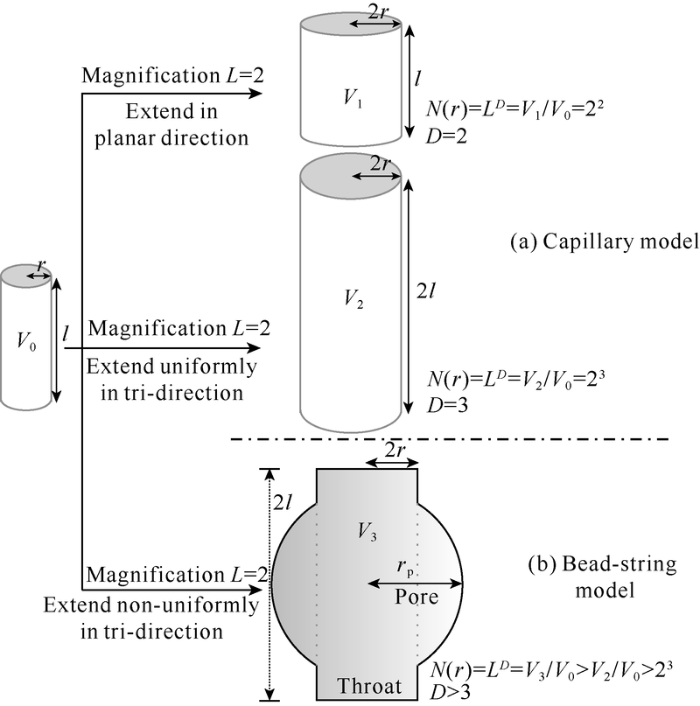
According to fractal theory, if an object extends in equal proportion to two directions, its fractal dimension is equal to 2, if it extends in equal proportion to 3 directions, its fractal dimension is 3; and if it extend in 3 directions in unequal proportions, its fractal dimension is more than 3 (Fig. 10). Therefore, the variation in fractal dimension can reflect features and differences in pore structure[27].
Fig. 10.
Fractal dimension of pore throat model with different extension pattern.
The 14 samples all show the fractal feature of two segments. The pore throats smaller than peak radius have fractal dimensions of 2 to 3, and the pore throats larger than the peak radius have fractal dimensions of over 3. Similar results have been previously reported[15,17]. It is generally believed that the pore throats with fractal dimension of 2 to 3 have fractal feature, while pore throats with fractal dimension of over 3 have no fractal feature[28,29,30]. Therefore, according to fractal theory, the pore throats in the tight sandstone samples tested have binary features:
When the pore throat is less than the peak radius (small and micro pore throat), the pore throat structure can be depicted by capillary model (Fig. 11), in which the pore radius approximately equals to throat radius. This is shown as small slope of the fitted straight line of lgpc and lgSHg. In this case, pore throat volume is determined by throat radius and increases slowly with the increase of pore throat radius. The fractal dimension is 2 to 3, suggesting that the pore throats extend between 2 dimensions and 3 dimensions, that is the length l of pore throat increases with the increase of radius r, but with the growth rate smaller than that of r. If the length l increases at the same growth rate with radius r, the fractal dimension would be equal to 3. In this case, the pore structure is self-affinity, or has fractal feature.
Fig. 11.
Binary pore structure model of tight sandstone.
When the pore throat radius is larger than the peak radius, the pore structure is similar to the bead-string model (Fig. 11a) and the pore radius is significantly larger than throat radius. As the throat size increases, the mercury volume increases rapidly, and the pores make much more contribution to pore throat volume than throats. In this case, the fractal dimension of large pore throat is over 3 (Fig.11b), indicating that pore structure is not uniformly distribute in three dimensions, and the shaper the slope of the linear relationship of lg SHg-lg pc is, the larger the ratio of pore radius to throat radius is.
Although the 14 samples in this study are different in petrology, porosity, permeability and pore throat size distribution, they all show binary pore structure, suggesting that this pore model is generally applicable.
4. Conclusions
Pore throats of the studied sandstone samples are less than 1 μm in radius and unimodal in distribution. Pore throats of different size scales have different influence on porosity and permeability. The big difference in large pore throat between the samples is the main factor causing porosity and permeability heterogeneity of tight sandstone. Large pore throats are also the main storage space for oil occurrence. Small and micro pore throats contribute major reservoir space, but are relatively stable, have little effect on the change of physical properties, and low correlation with oil saturation.
The tight sandstone has binary pore structure: when the pore throat radius is larger than the peak radius, the pore structure is similar to the bead-string model with no fractal feature, the pore size is much larger than throat size, and the pore throat volume is determined by the pore volume. When the pore throat radius is smaller than the peak radius, the pore structure is close to the capillary model and shows fractal feature, and the pore throat volume is determined by the throat radius.
The pore throats larger than the peak radius are mainly composed of secondary and intergranular pores. Therefore, even though the tight sandstone contains a large amount of small and micro pores, when evaluating physical properties of tight sandstone, features, origins and main controlling factors of large pores such as intergranular and dissolved pores should be analyzed as focus.
Nomenclature
C—intercept, dimensionless;
D—fractal dimension, dimensionless;
D1—fractal dimension of large pore throat, dimensionless;
D2—fractal dimension of small pore throat, dimensionless;
K—permeability, 10-3 μm2;
VHg—mercury injection volume, μm3;
l—capillary length, μm;
L—magnification, dimensionless;
N(r)—the number of the units, piece;
pc—mercury injection pressure, MPa;
r—capillary radius, μm;
rp —pore radius, μm;
R, R1 and R2—correlation coefficients, dimensionless;
SHg—mercury saturation, %;
V0, V1, V2and V3—pore throat volumes at different magnifications, μm3;
Vp —pore volume, μm3;
α—constant, dimensionless;
θ—contact angle, (°);
σ—interface tension, N/m;
ϕ—total porosity, %;
ϕ1—porosity of large pore throat, %;
ϕ2—porosity of small pore throat, %;
ϕ3—porosity of micro-pore throat, %;
ϕo—oil-bearing porosity, %.
Reference
Characteristics and influencing factors of movable fluid in ultra-low permeability sandstone reservoir
The evolution of pore-scale fluid-saturation in low-permeability sandstone reservoirs
DOI:10.1306/03041411168 URL [Cited within: 1]
Diagenetic controls on the reservoir quality of fine-grained “tight” sandstones: A case study based on NMR analysis
DOI:10.1016/j.saa.2019.117936
URL
PMID:31864151
[Cited within: 2]

TiO2 nanoparticles as solar cells and photocatalysts caused extensive attention in solar energy utilization and environment remediation due to the high photoelectrochemical performance. We demonstrated a novel approach to fabricate big-leaf hydrangea-like Bi2S3-BiOBr self-assembled by superthin nanosheets on TiO2 nanotube arrays (TiO2 NTs/B2S3-BiOBr). Results indicated that the Bi2S3-BiOBr co-sensitization showed higher photoelectric conversion efficiency than the single Bi2S3 or BiOBr sensitization. More remarkably, TiO2 NTs/B2S3-BiOBr showed excellent photoelectrocatalytic (PEC) removal of MB, MO, RhB and Cr(VI). The remarkable PEC performance could be attributed to the strong visible light absorption and effective electron transportation at the interface of TiO2/B2S3-BiOBr. The high photoelectrochemical performances indicate that the TiO2 NTs/B2S3-BiOBr could work as potential photoelectric materials for large-scale applications in the photoelectrochemical energy conversion and pollutant removal.
Movable fluid study of low permeability reservoir with nuclear magnetic resonance technology
The movable fluid evaluation was conducted based on a total of 277 matrix block samples from three typical domestic lowpermeability reservoirs of different lithologies, mainly using nuclear magnetic resonance(NMR) core analysis technique of low magnetic field and supplemented by other routine test means including rock thin section, environment scanning electron microscopy(ESEM), high-resolution computed tomography(CT) and imaging logging. The distribution law and influencing factors of reservoir movable fluid were analyzed, and the cutoff value for T2 and porethroat radius of movable fluid were calculated. The results show that the movable fluid parameters of low permeability reservoirs have wide range. The relation of the movable fluid parameters and the permeability gets better with the increase of permeability. The correlation among percentage of movable fluid, porosity, permeability is better in sandstone reservoirs. The values calculated by nonlinear optimization method well agreed with the measured values. Micropore structures, such as development degree of micro-fracture, pore size distribution, clay mineral and the filling degree, determine the distribution of movable fluids in low permeability reservoirs.
Pore structure characterization, permeability evaluation and enhanced gas recovery techniques of tight gas sandstones
DOI:10.1111/gcb.14970
URL
PMID:31863618
[Cited within: 2]

The effects of nitrogen (N) deposition on soil organic carbon (C) and greenhouse gas (GHG) emissions in terrestrial ecosystems are the main drivers affecting GHG budgets under global climate change. Although many studies have been conducted on this topic, we still have little understanding of how N deposition affects soil C pools and GHG budgets at the global scale. We synthesized a comprehensive dataset of 275 sites from multiple terrestrial ecosystems around the world and quantified the responses of the global soil C pool and GHG fluxes induced by N enrichment. The results showed that the soil organic C concentration and the soil CO2 , CH4 and N2 O emissions increased by an average of 3.7%, 0.3%, 24.3% and 91.3% under N enrichment, respectively, and that the soil CH4 uptake decreased by 6.0%. Furthermore, the percentage increase in N2 O emissions (91.3%) was two times lower than that (215%) reported by Liu & Greaver (2009). There was also greater stimulation of soil C pools (15.70 kg C ha-1 yr-1 per kg N/ha yr-1 ) than previously reported under N deposition globally. The global N deposition results showed that croplands were the largest GHG sources (calculated as CO2 equivalents), followed by wetlands. However, forests and grasslands were two important GHG sinks. Globally, N deposition increased the terrestrial soil C sink by 6.34 Pg CO2 per year. It also increased net soil GHG emissions by 10.20 Pg CO2 -Geq (CO2 equivalents) per year. Therefore, N deposition not only increased the size of the soil C pool but also increased global greenhouse gas emissions, as calculated by the global warming potential approach.
Pore-throat sizes in sandstones, tight sandstones, and shales
DOI:10.1038/srep36919
URL
PMID:27830731
[Cited within: 1]

Understanding the pore networks of unconventional tight reservoirs such as tight sandstones and shales is crucial for extracting oil/gas from such reservoirs. Mercury injection capillary pressure (MICP) and N2 gas adsorption (N2GA) are performed to evaluate pore structure of Chang-7 tight sandstone. Thin section observation, scanning electron microscope, grain size analysis, mineral composition analysis, and porosity measurement are applied to investigate geological control factors of pore structure. Grain size is positively correlated with detrital mineral content and grain size standard deviation while negatively related to clay content. Detrital mineral content and grain size are positively correlated with porosity, pore throat radius and withdrawal efficiency and negatively related to capillary pressure and pore-to-throat size ratio; while interstitial material is negatively correlated with above mentioned factors. Well sorted sediments with high debris usually possess strong compaction resistance to preserve original pores. Although many inter-crystalline pores are produced in clay minerals, this type of pores is not the most important contributor to porosity. Besides this, pore shape determined by N2GA hysteresis loop is consistent with SEM observation on clay inter-crystalline pores while BJH pore volume is positively related with clay content, suggesting N2GA is suitable for describing clay inter-crystalline pores in tight sandstones.
Petrophysical characterization of tight oil reservoirs using pressure-controlled porosimetry combined with rate-controlled porosimetry
DOI:10.1016/j.fuel.2015.03.085 URL [Cited within: 2]
Permeability in rotliegend gas sandstones to gas and brine as predicted from NMR, mercury injection and image analysis
DOI:10.1016/j.marpetgeo.2015.02.009 URL
Pore structure characterization of Chang-7 tight sandstone using MICP combined with N2GA techniques and its geological control factors
DOI:10.1038/srep36919
URL
PMID:27830731
[Cited within: 2]

Understanding the pore networks of unconventional tight reservoirs such as tight sandstones and shales is crucial for extracting oil/gas from such reservoirs. Mercury injection capillary pressure (MICP) and N2 gas adsorption (N2GA) are performed to evaluate pore structure of Chang-7 tight sandstone. Thin section observation, scanning electron microscope, grain size analysis, mineral composition analysis, and porosity measurement are applied to investigate geological control factors of pore structure. Grain size is positively correlated with detrital mineral content and grain size standard deviation while negatively related to clay content. Detrital mineral content and grain size are positively correlated with porosity, pore throat radius and withdrawal efficiency and negatively related to capillary pressure and pore-to-throat size ratio; while interstitial material is negatively correlated with above mentioned factors. Well sorted sediments with high debris usually possess strong compaction resistance to preserve original pores. Although many inter-crystalline pores are produced in clay minerals, this type of pores is not the most important contributor to porosity. Besides this, pore shape determined by N2GA hysteresis loop is consistent with SEM observation on clay inter-crystalline pores while BJH pore volume is positively related with clay content, suggesting N2GA is suitable for describing clay inter-crystalline pores in tight sandstones.
Diagenesis, porosity evolution, and petroleum emplacement in tight gas reservoirs, Taranaki Basin, New Zealand
DOI:10.2110/jsr.2007.095 URL [Cited within: 1]
A review on pore structure characterization in tight sandstones
DOI:10.1016/j.earscirev.2017.12.003 URL [Cited within: 1]
Characterization of Brazilian tight gas sandstones relating permeability and Angstrom-to micron-scale pore structures
DOI:10.1111/gcb.14970
URL
PMID:31863618
[Cited within: 1]

The effects of nitrogen (N) deposition on soil organic carbon (C) and greenhouse gas (GHG) emissions in terrestrial ecosystems are the main drivers affecting GHG budgets under global climate change. Although many studies have been conducted on this topic, we still have little understanding of how N deposition affects soil C pools and GHG budgets at the global scale. We synthesized a comprehensive dataset of 275 sites from multiple terrestrial ecosystems around the world and quantified the responses of the global soil C pool and GHG fluxes induced by N enrichment. The results showed that the soil organic C concentration and the soil CO2 , CH4 and N2 O emissions increased by an average of 3.7%, 0.3%, 24.3% and 91.3% under N enrichment, respectively, and that the soil CH4 uptake decreased by 6.0%. Furthermore, the percentage increase in N2 O emissions (91.3%) was two times lower than that (215%) reported by Liu & Greaver (2009). There was also greater stimulation of soil C pools (15.70 kg C ha-1 yr-1 per kg N/ha yr-1 ) than previously reported under N deposition globally. The global N deposition results showed that croplands were the largest GHG sources (calculated as CO2 equivalents), followed by wetlands. However, forests and grasslands were two important GHG sinks. Globally, N deposition increased the terrestrial soil C sink by 6.34 Pg CO2 per year. It also increased net soil GHG emissions by 10.20 Pg CO2 -Geq (CO2 equivalents) per year. Therefore, N deposition not only increased the size of the soil C pool but also increased global greenhouse gas emissions, as calculated by the global warming potential approach.
Micro pore and throat characteristics and origin of tight sandstone reservoirs: A case study of the Triassic Chang 6 and Chang 8 members in Longdong area, Ordos Basin, NW China
DOI:10.1016/j.jhazmat.2019.121845
URL
PMID:31862354
[Cited within: 2]

Polycyclic aromatic hydrocarbons (PAH) are organic pollutants that require remediation due to their detrimental impact on human and environmental health. In this study, we used a novel approach of sequestering a model PAH, phenanthrene, onto a solid carbon matrix bioanode in a microbial fuel cell (MFC) to assess its biodegradation coupled with power generation. Here, the bioanode serves as a site for enrichment of electroactive and hydrocarbon-degrading microorganisms, which can simultaneously act to biodegrade a pollutant and generate power. Carbon cloth electrodes loaded with two rates of phenanthrene (2 and 20 mg cm-2) were compared using dual chamber MFCs that were operated for 50 days. The lower loading rate of 2 mg cm-2 was most efficient in the degradation of phenanthrene and had higher power production capacities (37 mW m-2) as compared to the higher loading rate of 20 mg cm-2 (power production of 19.2 mW m-2). FTIR (Fourier-Transform Infrared Spectroscopy) analyses showed a depletion in absorbance peak signals associated with phenanthrene. Microbes known to have electroactive properties or phenanthrene biodegradation abilities like Pseudomonas, Rhodococcus, Thauera and Ralstonia were enriched over time in the MFCs, substantiating the electrochemical and FTIR analyses. The MFC approach taken here thus offers great promise towards PAH bioelectroremediation.
Combining pressure-controlled porosimetry and rate-controlled porosimetry to investigate the fractal characteristics of full-range pores in tight oil reservoirs
DOI:10.1016/j.petrol.2018.07.050 URL [Cited within: 2]
Insight into the pore structure of tight sandstones using NMR and HPMI measurements
DOI:10.1016/j.saa.2019.117936
URL
PMID:31864151
[Cited within: 3]

TiO2 nanoparticles as solar cells and photocatalysts caused extensive attention in solar energy utilization and environment remediation due to the high photoelectrochemical performance. We demonstrated a novel approach to fabricate big-leaf hydrangea-like Bi2S3-BiOBr self-assembled by superthin nanosheets on TiO2 nanotube arrays (TiO2 NTs/B2S3-BiOBr). Results indicated that the Bi2S3-BiOBr co-sensitization showed higher photoelectric conversion efficiency than the single Bi2S3 or BiOBr sensitization. More remarkably, TiO2 NTs/B2S3-BiOBr showed excellent photoelectrocatalytic (PEC) removal of MB, MO, RhB and Cr(VI). The remarkable PEC performance could be attributed to the strong visible light absorption and effective electron transportation at the interface of TiO2/B2S3-BiOBr. The high photoelectrochemical performances indicate that the TiO2 NTs/B2S3-BiOBr could work as potential photoelectric materials for large-scale applications in the photoelectrochemical energy conversion and pollutant removal.
Micro/nanoscale pore structure and fractal characteristics of tight gas sandstone: A case study from the Yuanba area, northeast Sichuan Basin, China
DOI:10.1016/j.marpetgeo.2018.08.013 URL [Cited within: 2]
A simple method to estimate complete pore size distribution of rocks
DOI:10.1016/j.enggeo.2005.11.009 URL [Cited within: 2]
Analytical derivation of Brooks-Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity
DOI:10.1016/j.petrol.2010.05.002 URL [Cited within: 1]
Microscopic occurrence of oil in tight sandstones and its relation with oil sources: A case study from the Upper Triassic Yanchang Formation, Ordos Basin
DOI:10.1016/j.foodchem.2019.125957
URL
PMID:31864191
[Cited within: 1]

The main aim of this work was to characterize the volatile profile of virgin pistachio oils produced from eight cultivars (Aegina, Avdat, Kastel, Kerman, Larnaka, Mateur, Napoletana and Sirora), under different technological conditions (temperature, roasting, use of whole nuts, screw speed and nozzle diameter), and compare it with those of commercial pistachio oils. Terpenes (15.57-41.05 mg/kg), accounting for ~97% of total volatiles, were associated with appreciated sensory properties, with α-pinene as the main volatile (14.47-37.09 mg/kg). Other terpene compounds such as limonene (0.11-3.58 mg/kg), terpinolene (0.00-1.61 mg/kg), β-pinene (0.12-1.20 mg/kg) and α-terpineol (0.00-1.17 mg/kg) were quantified at lower concentrations. Acids, alcohols, aldehydes, esters and hydrocarbons only summed to ~3% of the total volatile compounds. The volatiles content greatly depended on the pistachio cultivar employed. The influence of extraction conditions was also very relevant; in particular, terpenes doubled (28.38-53.84 mg/kg) using whole pistachios for oil extraction, also being incremented by mild processing conditions. On the contrary, higher temperature or roasting decreased the terpene content (~50-25% respectively), and pyrazines appeared (up to 3.12 mg/kg).
Tight oil occurrence space of Triassic Chang 7 Member in Northern Shaanxi Area, Ordos Basin, NW China
Do shale pore throats have a threshold diameter for oil storage?
DOI:10.1038/srep13619
URL
PMID:26314637
[Cited within: 1]

In this work, a nanoporous template with a controllable channel diameter was used to simulate the oil storage ability of shale pore throats. On the basis of the wetting behaviours at the nanoscale solid-liquid interfaces, the seepage of oil in nano-channels of different diameters was examined to accurately and systematically determine the effect of the pore diameter on the oil storage capacity. The results indicated that the lower threshold for oil storage was a pore throat of 20 nm, under certain conditions. This proposed pore size threshold provides novel, evidence-based criteria for estimating the geological reserves, recoverable reserves and economically recoverable reserves of shale oil. This new understanding of shale oil processes could revolutionize the related industries.
Petrography and reservoir physics II: Relating thin section porosity to capillary pressure, the association between pore types and throat size
Oil charge preserves exceptional porosity in deeply buried, overpressured, sandstones: Central North Sea, UK
DOI:10.1144/0016-76492011-007 URL [Cited within: 1]
The effect of oil emplacement on quartz cementation in a deeply buried sandstone reservoir
DOI:10.1306/02071716001 URL [Cited within: 2]
Reprint of: Diagenetic controls on evolution of porosity and permeability in lower Tertiary Wilcox sandstones from shallow to ultradeep (200-6700 m) burial, Gulf of Mexico Basin, U.S.A
DOI:10.1016/j.scitotenv.2019.135978
URL
PMID:31864138
[Cited within: 1]

Scientific evidences abound of the occurrence of plastic pollution, from mega- to nano-sized plastics, in virtually all matrixes of the environment. Apart from the direct effects of plastics and microplastics pollution such as entanglement, inflammation of cells and gut blockage due to ingestion, plastics are also able to act as vectors of various chemical contaminants in the aquatic environment. This paper provides a review of the association of plastic additives with environmental microplastics, how the structure and composition of polymers influence sorption capacities and highlights some of the models that have been employed to interpret experimental data from recent sorption studies. The factors that influence the sorption of chemical contaminants such as the degree of crystallinity, surface weathering, and chemical properties of contaminants. and the implications of chemical sorption by plastics for the marine food web and human health are also discussed. It was however observed that most studies relied on pristine or artificially aged plastics rather than field plastic samples for studies on chemical sorption by plastics.
Diagenetic controls on reservoir quality of tight sandstone: A case study of the Upper Triassic Yanchang formation Chang 7 sandstones, Ordos Basin, China
DOI:10.15446/esrj.v22n2.72251 URL [Cited within: 1]
Fractal measurements of sandstones, shales, and carbonates
Capillary pressure, water relative permeability, electrical conductivity and capillary dispersion coefficient of fractal porous media at low wetting phase saturations
DOI:10.2118/23675-PA URL [Cited within: 1]
Reservoir spaces in tight sandstones: Classification, fractal characters, and heterogeneity
DOI:10.1016/j.jngse.2017.07.006 URL [Cited within: 1]
Fractal sandstone pores: Implications for conductivity and pore formation
DOI:10.1103/PhysRevLett.54.1325 URL PMID:10030996 [Cited within: 1]