History matching by use of optimal theory
1
1975
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
Automatic history matching with variable-metric methods
1
1988
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
Coupled inverse problems in groundwater modeling: 1. Sensitivity analysis and parameter identification
1
1990
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
A general history matching algorithm for three-phase, three-dimensional petroleum reservoirs
1
1993
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
An initial guess for the Levenberg-Marquardt algorithm for conditioning a stochastic channel to pressure data
1
2003
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
A novel assisted history matching workflow and application on a full field reservoir simulation model
1
2019
... Manual history matching is a time consuming and often frustrating process[1,2,3,4,5]. In recent years, several approaches have been introduced to automate several tasks of the process. The concept of the assisted history matching is as simple as converting the history matching problem to an optimization problem with the objective of minimizing the difference between actual observations (e.g. pressure, rate, and saturation distribution) and simulated data. The workflow of assisted history matching is usually composed of three main elements: experimental design, proxy modeling, and optimization. Shams et al.[6] proposed a detailed description of the assisted history matching process and a newly workflow. ...
A new heuristic optimization algorithm: Harmony search
4
2001
... HSO is a stochastic optimization algorithm developed by Geem et al.[7] and inspired by harmony improvisation of musicians searching for the best harmonious performance[8]. Likewise, an optimal solution of an optimization problem is the best solution available of the problem under the given objectives and the predefined constraints. Similarities between the two processes were used to develop the new optimization algorithm, namely, HSO, which has never been used before in reservoir engineering questions. ...
... As mentioned above, HSO algorithm is inspired by harmony improvisation of musicians searching for the best harmonious performance. The music harmony improvisation process is usually divided three steps: (1) Selecting a satisfactory pitch of music from the musicians’ memory; (2) Selecting a pitch of music similar to the satisfactory pitch and then adjusting slightly; (3) Composing a new or random pitch. The sets of better harmony are memorized and the poor sets are discarded. The harmony sets are updated continuously until the best harmony is achieved. The three steps of the music harmony improvisation process were formalized by Geem et al.[7] in an attempt to mimic the inherent optimization procedure, that is the harmony search optimization algorithm (HSO). The steps of HSO algorithm are as follows: firstly, initializing the harmony memory. Then generate new solution vectors, and their components can be generated by 3 mechanisms, namely, (1) keeping some components in the harmony memory, with a retention probability of harmony memory as HMCR; (2) Generating some components stochastically, with the probability of 1-HMCR, (3) Adjusting the new components from (1) and (2), if the evaluation function of the new solution vector is better than the worst solution in the harmony memory, then the new solution vector is used to replace the worst solution; and the calculations ends when the terminal conditions are met (for example, reaching the maximum iterative times). The main control factors of HSO algorithm are the size and retention probability of harmony memory and pitch adjustment probability (PAR). ...
... (2) Retention probability of harmony memory (HMCR): Value selection in a harmony memory is like the process of musician selecting a satisfactory pitch to ensure the rendition of good music piece. In HSO, HMCR selects the best fit solution value for each variable to ensure the carrying-over of the best harmony to the new harmony memory. HMCR is a probability in the range of 0 to 1. If the HMCR selected is too low, only a few best harmonies are selected, and the convergence may be slow. If the HMCR selected is too high (close to 1), almost all the harmonies are used in the harmony memory and then other harmonies are not explored well. This may lead to potentially wrong solutions. Therefore, in most applications, HMCR is set between 0.70 and 0.95[7]. ...
... (3) Pitch adjustment probability (PAR). Pitch adjustment is similar to playing a pitch of music similar to a satisfactory music piece. In HSO, pitch adjustment is equivalent to the process of creating a slightly different solution. By adjusting a pitch stochastically, a new solution is created around an existing good solution. By applying PAR (0-1) to control the degree of adjustment. If a low adjusting rate parameter with a narrow bandwidth is assigned, the search will be limited in a sub-space of the search space, and then the convergence of the harmony search will decrease. Conversely, if a high adjusting rate parameter with a wide bandwidth is assigned, the probability of having scattered solutions around potential optima will increase. Thus, the PAR is set between 0.1 and 0.5 in most cases[7]. ...
Improvement of Levenberg- Marquardt algorithm during history fitting for reservoir simulation
2
2016
... HSO is a stochastic optimization algorithm developed by Geem et al.[7] and inspired by harmony improvisation of musicians searching for the best harmonious performance[8]. Likewise, an optimal solution of an optimization problem is the best solution available of the problem under the given objectives and the predefined constraints. Similarities between the two processes were used to develop the new optimization algorithm, namely, HSO, which has never been used before in reservoir engineering questions. ...
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Use of parameter gradients for reservoir history matching
1
1989
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Schemes for automatic history matching of reservoir modeling: A case of Nelson oilfield in UK
1
2012
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Enhancing gas reservoir characterization by simulated annealing method (SAM)
1
1992
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Simulated annealing for interpreting gas/water laboratory
1
1992
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
A new algorithm for automatic history matching: Application of simulated annealing method (SAM) to reservoir inverse modeling
1
1993
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Stochastic reservoir modeling using simulated annealing and genetic algorithms
1
1995
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Adaptation in natural and artificial systems
1
1975
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Top-down reservoir modeling
1
2004
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
History matching and uncertainty quantification assisted by global optimization techniques
1
2006
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Integrated development optimization model and its solving method of multiple gas fields
1
2016
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Evolutionary algorithm based approach for modeling autonomously trading agents
1
2014
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Data assimilation coupled to evolutionary algorithms: A case example in history matching
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Use of parameter gradients for reservoir history matching
1
1989
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
New era of history matching and probabilistic forecasting: A case study
1
2006
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Scatter search metaheuristic applied to the history-matching problem
1
2006
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
A learning computational engine for history matching
1
2006
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
A parallelized and hybrid data-integration algorithm for history matching of geologically complex reservoirs
1
2016
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Investigation of stochastic optimization methods for automatic history matching of SAGD processes
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Critical evaluation of the ensemble Kalman filter on history matching of geological facies
1
2005
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Comparing different ensemble Kalman filter approaches
1
2008
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Generalization of the ensemble Kalman filter using kernels for non-Gaussian random fields
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Stochastic optimization using EA and EnKF: A comparison
1
2008
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Localization in the ensemble Kalman Filter
1
2008
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Comparison of sequential data assimilation methods for the Kuramoto-Sivashinsky Equation
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Analysis of the ensemble Kalman Filter for estimation of permeability and porosity in reservoir models
1
2005
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Ensemble Kalman filtering versus sequential self-calibration for inverse modeling of dynamic groundwater flow systems
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Particle swarm optimization: Proceedings of IEEE International Conference on Neural Networks
1
1995
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Population-based algorithms for improved history matching and uncertainty quantification of petroleum reservoirs
1
2011
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Uncertainty evaluation of reservoir simulation models using particle swarm and hierarchical clustering
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Comparison of stochastic sampling algorithms for uncertainty quantification
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Application of particle swarm optimization to reservoir modeling and inversion
1
2009
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
Application of Lorenz-curve model to stratified water injection evaluation
1
2015
... Optimization algorithms include two categories: deterministic and stochastic algorithms[8]. Deterministic optimization is the classical approach of optimization methods which completely depends on linear algebra. In deterministic optimization, the gradient of the mathematical model is calculated to optimize the parameter to minimize the objective function. The solution of this kind of algorithm is a local optimum but not the global optimum. A local optimum maxima or minima is not the real optimal solution. Due to the non-uniqueness nature of the history matching questions, we expect to have several local minima, and therefore the deterministic algorithms can’t work effectively in solving this kind of question[9]. In contrast, the stochastic optimization concept is based on employing randomness in the search procedure[10]. Several stochastic optimization algorithms, such as simulated annealing[11,12,13], heat-bath algorithm[14], GA[15,16,17,18], evolutionary strategy[19,20,21,22], scatter search optimization[23], simultaneous perturbation stochastic approximation[24,25,26], ensemble Kalman filters[27,28,29,30,31,32,33,34], PSO[35], ant colony algorithm[36], have been tested in reservoir engineering assisted history matching[37,38,39,40]. In this work, HSO algorithm was introduced into assisted history matching of reservoir engineering and compared with two other optimization algorithms (GA and PSA) commonly used in this kind of research. ...
A comparison study of harmony search and genetic algorithm for the max-cut problem
1
2019
... In comparison, the quality of GA optimization results highly depends on the probabilities of genetic operators (crossover, selection, mutation) and is greatly affected by the tuning ways of these parameters. In addition, the tuning process of GA parameters is a pure random process and depends on trial and error. Also, if the population size assigned to an optimization question utilizing GA is too small, there won’t be enough evolution to go on. There will be a high risk that the whole population set is dominated by a limited number of individuals, which may lead to premature convergence and meaningless solutions[41]. Clerc and Kennedy[42] pointed out that the theoretical mathematical foundation of PSO algorithm was not strong enough. They analyzed the stability of the PSO transmitting matrix and found that there were a limited number of conditions under which the particle could move stably. In addition, according to Shailendra[43], the PSO algorithm would fall into stagnation once the particles have prematurely converged to any particular region of the search space. He also found that PSO algorithm had higher efficiency with small number of particles, but when the number of particles increases, the algorithm became worse in performance. This can be a question in reservoir history matching questions as they usually have many unknown variables to optimize. ...
The particle swarm-explosion stability and convergence in a multidimensional complex space
1
2002
... In comparison, the quality of GA optimization results highly depends on the probabilities of genetic operators (crossover, selection, mutation) and is greatly affected by the tuning ways of these parameters. In addition, the tuning process of GA parameters is a pure random process and depends on trial and error. Also, if the population size assigned to an optimization question utilizing GA is too small, there won’t be enough evolution to go on. There will be a high risk that the whole population set is dominated by a limited number of individuals, which may lead to premature convergence and meaningless solutions[41]. Clerc and Kennedy[42] pointed out that the theoretical mathematical foundation of PSO algorithm was not strong enough. They analyzed the stability of the PSO transmitting matrix and found that there were a limited number of conditions under which the particle could move stably. In addition, according to Shailendra[43], the PSO algorithm would fall into stagnation once the particles have prematurely converged to any particular region of the search space. He also found that PSO algorithm had higher efficiency with small number of particles, but when the number of particles increases, the algorithm became worse in performance. This can be a question in reservoir history matching questions as they usually have many unknown variables to optimize. ...
A brief review on particle swarm optimization: Limitations and future directions
1
2013
... In comparison, the quality of GA optimization results highly depends on the probabilities of genetic operators (crossover, selection, mutation) and is greatly affected by the tuning ways of these parameters. In addition, the tuning process of GA parameters is a pure random process and depends on trial and error. Also, if the population size assigned to an optimization question utilizing GA is too small, there won’t be enough evolution to go on. There will be a high risk that the whole population set is dominated by a limited number of individuals, which may lead to premature convergence and meaningless solutions[41]. Clerc and Kennedy[42] pointed out that the theoretical mathematical foundation of PSO algorithm was not strong enough. They analyzed the stability of the PSO transmitting matrix and found that there were a limited number of conditions under which the particle could move stably. In addition, according to Shailendra[43], the PSO algorithm would fall into stagnation once the particles have prematurely converged to any particular region of the search space. He also found that PSO algorithm had higher efficiency with small number of particles, but when the number of particles increases, the algorithm became worse in performance. This can be a question in reservoir history matching questions as they usually have many unknown variables to optimize. ...
Schedule optimization to complement assisted history matching and prediction under uncertainty
1
2006
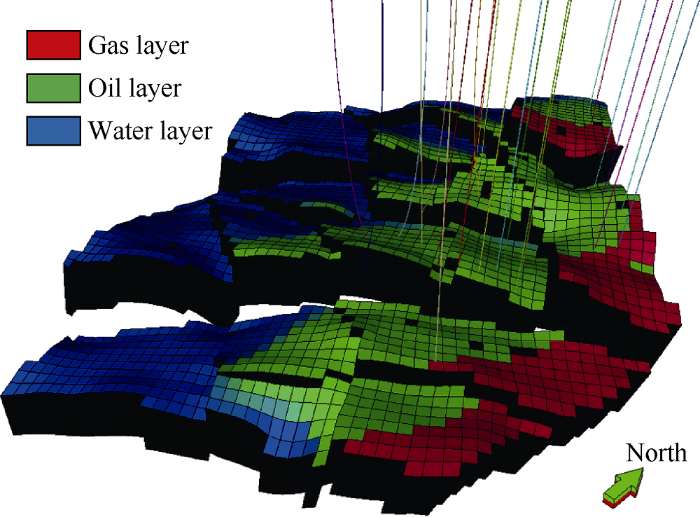
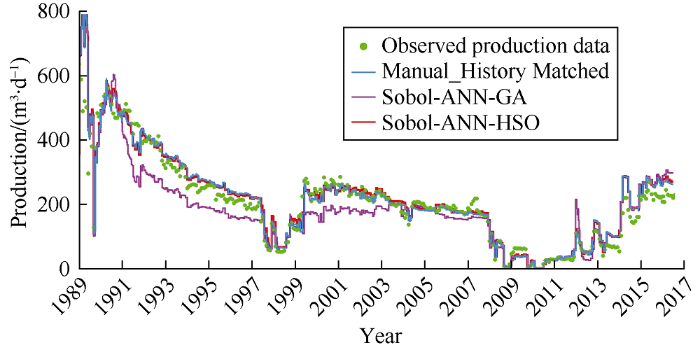
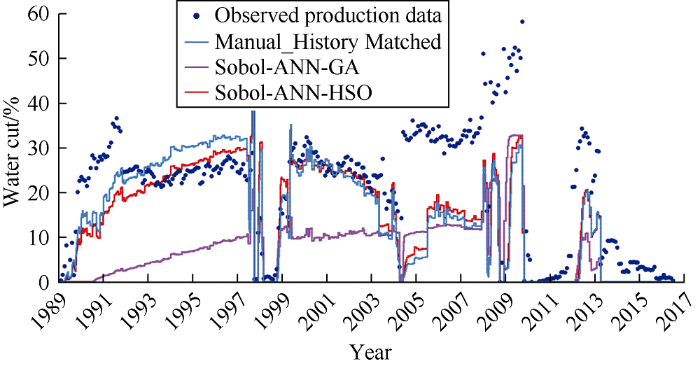
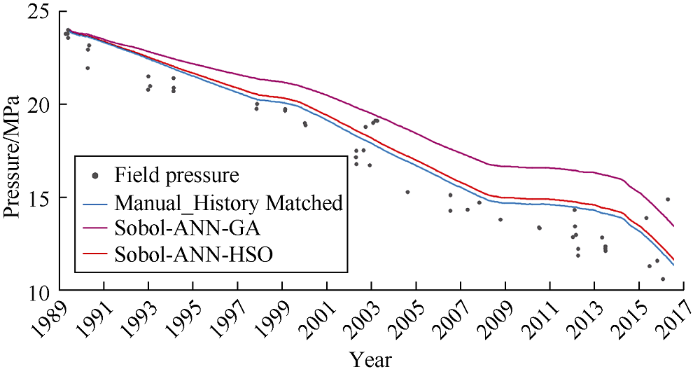
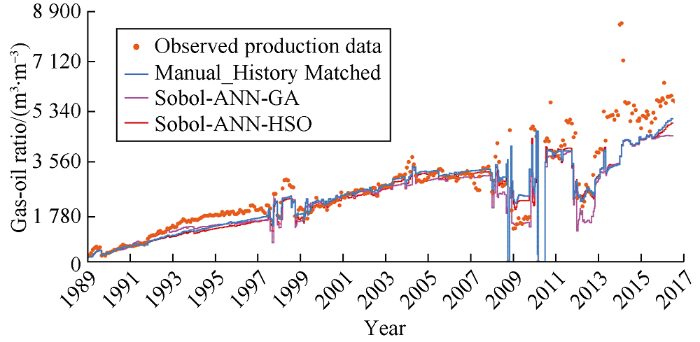
... The 15 parameters used in the assisted history matching and manual history matching are shown in Table 2. The workflow of assisted history matching is as follows: (1) Use Sobol sequence experimental design technique to select 25 sample runs out of the uncertainty range of the assigned history matching parameters. (2) The scoping runs contains 26 runs (25 selected by the experimental design method and the rest one represents the most likely values of the history matching parameters) following JUTILA’s rule of thumb[44] that states that the number of scoping runs should not be less than (2N+1) with upper limit of 26 runs. (3) Run the scoping runs over the first half of the historical data (first 14 years). For each scoping run, a multiple objective function was calculated with equation (2). (4) In the proxy model built by ANN, the objective function and the experimentally designed reservoir parameter samples were interpolated. (5) The created ANN proxy model was minimized by HSO and GA. The minimization process was run five times to take a more representative solution by each algorithm. (6) Use the values of the history matching parameters obtained by the two algorithms as input for running the next half of the history matching (last 14 years) in prediction mode. (7) Compare the simulated data of each workflow with the actual data by using the error indicator calculated with equation (4). (8) Petrel and ECLIPSE commercial software programs were used for reservoir simulation of the field case and then MATLAB was used to run the coded assisted history matching workflow. ...