Introduction
Converted from depleted gas reservoirs, gas reservoir-type underground gas storages[1,2] have the advantage of centralized management, large working gas volume, and good economic benefit. Due to an increase in demand, water-invaded gas reservoirs, with edge water and bottom water emerging in the process of sealed preservation and geologic evolution, have inevitably become the targets for gas storage. After the gas reservoir is changed into gas storage, individual-well operating mode is changed from low-speed depletion recovery to high-speed multiple cycles of injection and production[3,4], which would complicate multi-phase fluid flow and coexistence in pore space[5,6]. Relative permeability hysteresis effect often results from the variation of fluid relative permeability after single imbibition or displacement, and such variation is closely related to rock wettability as well as physical properties and flow mode of the fluid[7]. Relative permeability hysteresis effect in multi-cycle injection and production of the gas storage originates from bidirectional injection and production typical for the gas storage. Displacement alternates with imbibition repeatedly in the same area of the gas storage, with fluid flow characteristics changing, the process would consequently affect the storage capacity, individual-well injection-production capacity, cycle of capacity expansion to reach designed production, well type and well pattern design, and injection-production management of the gas storage[8,9]. This means that objective description of relative permeability hysteresis effect in multi-cycle injection and production is the basis for building reliable numerical model, and a prerequisite to fluid distribution characterization and prediction of performance indexes.
There has been extensive research into relative permeability hysteresis effect. Osoba et al.[10] used experiments to demonstrate that an oil reservoir with gas cap was better characterized by using displacement relative permeability curve while an oil reservoir with bottom water by imbibition relative permeability curve. Land[11] formulated the functional relationship between the saturation after non-wetting phase imbibition and initial saturation. Killough[12] established the mathematical model of the hysteresis curve based on the capillary force and relative permeability hysteresis effect obtained from experiments. Owing to the progress in experimental techniques, Kadet et al.[13] obtained relative permeability hysteresis curve with considerable accuracy for two-phase oil-water fluid; Carlson[14] and Ranaee et al.[15] improved the theory of hysteresis. At present, some reservoir numerical simulators have integrated theoretical hysteresis models into the system. Kossack[16] compared different classic hysteresis models in numerical simulators. Mahzari[17] improved the accuracy of numerical history matching by modifying the experimental techniques for water-wet and mixed-wet systems and calibrating the hysteresis model. Ismail et al.[18] used production data to investigate the impacts of hysteresis effect on the history matching for gas reservoir development. Juanes et al.[19] evaluated the influence of relative permeability hysteresis effect on CO2 storage. Spiteri et al.[20] used numerical simulation to analyze the influence of relative permeability hysteresis effect on EOR through alternating gas-water displacement.
Physical experiments of relative permeability hysteresis effect have been aimed at the fluid systems of oil-water, gas-oil, and CO2-brine. Shi et al.[21] accomplished relative permeability measurement for multi-cycle alternating gas-water displacement preliminarily. Numerical simulations have focused on EOR through unidirectional alternating gas-water displacement and CO2 storage, but there are few studies on numerical simulation of relative permeability hysteresis during bidirectional multi-cycle alternating displacement in gas reservoir-type storage. Our efforts focus on relative permeability of two-phase gas-water fluids based on relative permeability measurement for multi-cycle alternating gas-water displacement using natural cores acquired from a gas reservoir-type storage. We formulate the numerical simulation method to correct relative permeability hysteresis during multi-cycle injection and production and evaluate the impacts of hysteresis effect on fluids distribution in the gas storage and its performance indexes.
1. Mechanism of relative permeability hysteresis during multi-cycle injection and production
1.1. Overview of relative permeability hysteresis
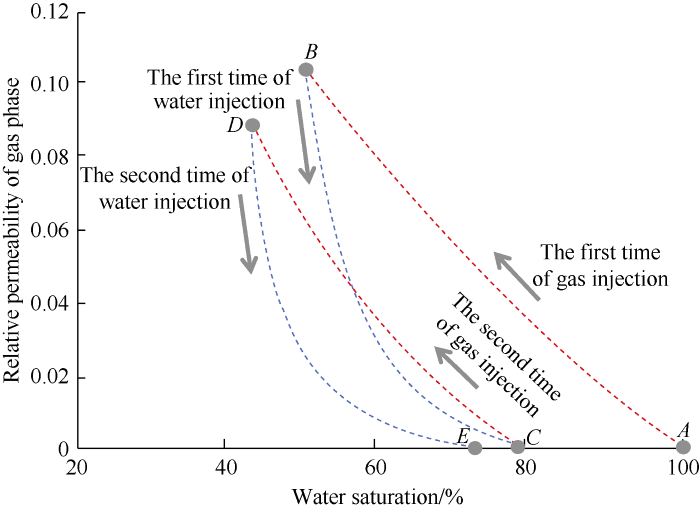
Relative permeability change, which occurs in gas- water flow in rocks, is related to rock wettability[22], capillary number, fluid saturation, and pore structure[23]. In general, wet angle variation at gas-water-rock interfaces causes wetting hysteresis, and wetting hysteresis, irregular inner surface of pores, and throat radius change induce capillary pressure hysteresis[24]. These hysteresis effects have a great impact on multi-phase fluid flow in pores. In addition, during the imbibition process of hydrophilic rock, as the saturation of the wetting phase (water phase) increases quickly, the non-wetting phase (gas phase) is scattered by the wetting phase into discrete phase in the form of slugs and gas bubbles; this will cause a change in the flow capacity of the non-wetting phase. During the operation of a water-invaded underground gas storage, gas is repeatedly injected and produced at high speed in individual wells, thus gas and water in the reservoir fully accord with alternating displacement-imbibition behavior mechanism, which would result in relative permeability hysteresis effect during multi-cycle injection and production of the gas storage (Fig. 1). The segment AB corresponding to gas displacing water (displacement) for the first time represents the process of gas accumulation. In the segment BC corresponding to water displacing gas (imbibition) for the first time, the water saturation at C is lower than the initial water saturation A. The segment CD corresponds to gas displacing water for the second time. In the segment DE corresponding to water displacing gas for the second time, the water saturation at E is lower than that at C. In this process of alternating gas-water displacement, the relative permeability curve, except for the change of end point value, is dependent on the path of injection and production. The relative permeability of gas decreases in the whole process, exhibiting hysteresis effect.
Fig. 1.
Fig. 1.
Schematic relative permeability hysteresis curves of gas.
1.2. Relative permeability experiments for multi-cycle alternating gas-water displacement
Twenty-four samples with the diameter of 2.5 cm and length of 5.0 cm were prepared using full-diameter (10.0 cm) natural cores acquired from a water-invaded sandstone gas storage. Three representative samples, corresponding to low-permeability, middle-permeability, and high-permeability reservoir rocks, were selected for petrophysical testing after drying. The permeability was tested to be 1.65×10-3 μm2, 19.34×10-3 μm2, and 49.00×10-3 μm2, respectively, and the porosity was tested to be 4.6%, 13.8%, and 16.5%, respectively. Gas-water relative permeability was tested in terms of the national standard (GB/T 28912-2012, Test method for two phase relative permeability in rock[25]) to simulate the process of multi-cycle gas-water displacement-imbibition in a gas storage. The detailed steps include: (1) The core sample was vacuumed and then saturated with simulated formation water. (2) Gas displacing water (simulated gas injection) at one end of the core, the displacement pressure difference was optimized, displacement pressure, gas output, and water output at each time point were recorded until the core reached the state of irreducible water (water output less than 0.1 mL/h), and then gas-phase effective permeability in the state of irreducible water was tested, and the gas displacing water was over. (3) Water displacing gas (simulated gas recovery), at the other end of the core with the volume of water displacement 20 pore volume, water-phase effective permeability in the state of residual gas before the end of water displacing gas. (4) Steps (2) and (3) were repeated until the rate of relative permeability change was smaller than 3% at the same water saturation.
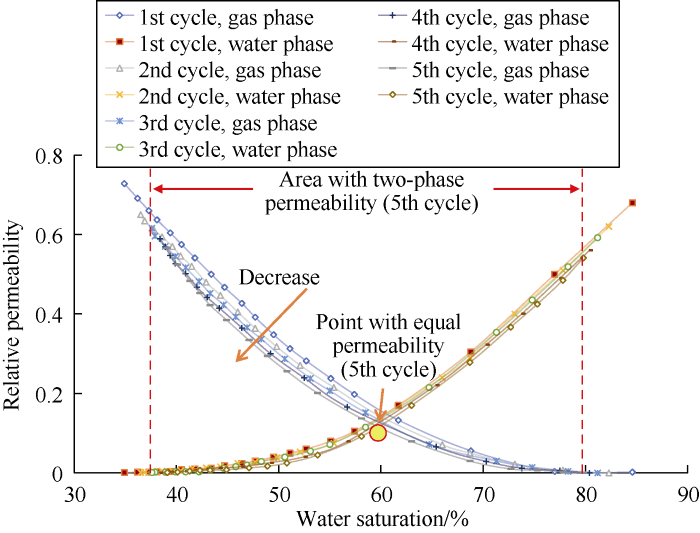
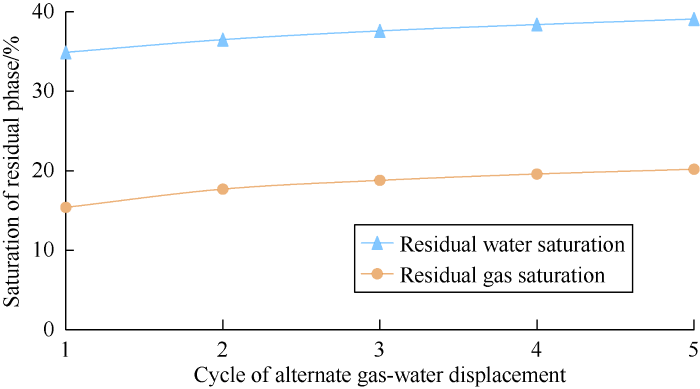
As per the experiments, the points with equal permeability in the relative permeability curves moving down due to increased cycles of injection and production, and the area with two-phase permeability shrinks. Take the core with the permeability of 19.34×10-3 μm2 as an example, the relative permeability of gas phase decreased significantly in the first three injection-production cycles (Fig. 2). In the fifth cycle, the relative permeability of gas phase decreased slower than the last cycle. The residual gas saturation tended to increase with multi-cycle injection and production process, and gradually tended to stabilize over the whole process (Fig. 3). The water phase, as the wetting phase in these experiments, reduced somewhat in relative permeability, indicating slight hysteresis effect.
Fig. 2.
Fig. 2.
Relative permeability hysteresis curves during multi- cycle alternating gas-water displacement.
Fig. 3.
Fig. 3.
Variation curves of residual water saturation during multi-cycle gas displacement and residual gas saturation during multi-cycle water displacement.
2. Numerical simulation correction of relative permeability hysteresis in multi-cycle injection and production
2.1. Numerical simulation of relative permeability hysteresis
In the numerical simulation of relative permeability hysteresis in displacement and imbibition between non- wetting phase and wetting phase in gas storage, it is difficult to obtain permeability-saturation curves for all cycles using laboratory physical experiments in view of low efficiency and high cost. An alternative way is to calculate the relative permeability hysteresis curve based on experimental results and mathematical model.
Introducing the critical saturation Sgc at the point when the non-wetting phase begins to flow, we can get:
The relation of relative permeability is
Using this method, we could calculate the saturation of the residual non-wetting phase and obtain the hysteresis curve and endpoint values of the imbibition process.
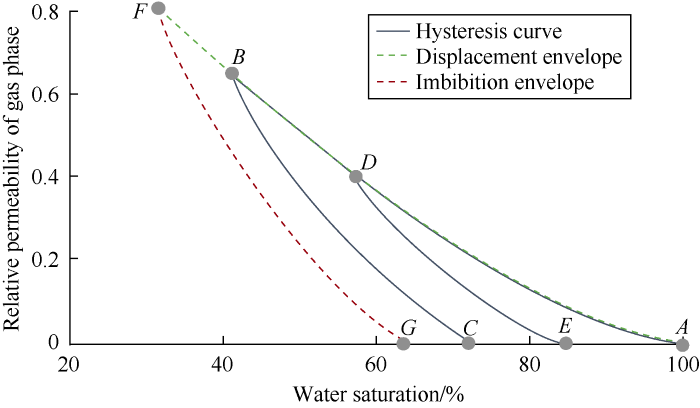
Eliminating complex processes of sampling and calculation, the Carlson model[14] has the advantage of obtaining imbibition curves for multi-cycle injection and production with high efficiency. Its mathematical principle is shown in Fig. 4. In accordance with the envelope FG for non-wetting phase imbibition obtained in lab test and endpoints B and D of the relative permeability curves for different cycles of displacement, curves DE and BC for non-wetting phase imbibition intersecting the axis of water saturation are plotted in parallel with the envelope to obtain the relative permeability curves during intermediate process of multi-cycle displacement and imbibition. The prerequisite of this method is to obtain the relative permeability curve for the imbibition process through lab test[14]; and the relative permeability of non-wetting phase in the process of imbibition is smaller than that in the process of displacement at the same water saturation.
Fig. 4.
Fig. 4.
Principle of Carlson mathematical model of relative permeability hysteresis (according to Reference [14]).
Numerical simulation of relative permeability hysteresis in multi-cycle injection and production of gas storage is fulfilled in the following steps. (1) Determine the envelopes for the displacement and imbibition processes using the relative permeability curve for the 2nd cycle of displacement after simulated gas accumulation in the core test and the imbibition relative permeability curve obtained when multi-cycle alternating gas-water displacement was stable. (2) Calculate the relative permeability curves between the envelopes to restore fluid flow state in each cycle of injection and production during numerical simulation. Intra-envelope hysteresis curves represent multi-phase fluid flow capacity variation during multi-cycle operation of the gas storage. The mathematical model of relative permeability hysteresis should be established by history matching results of production data or optimized in accordance with new mechanism. (3) Establish an accurate model for numerical simulation to accomplish the scheme design and result prediction.
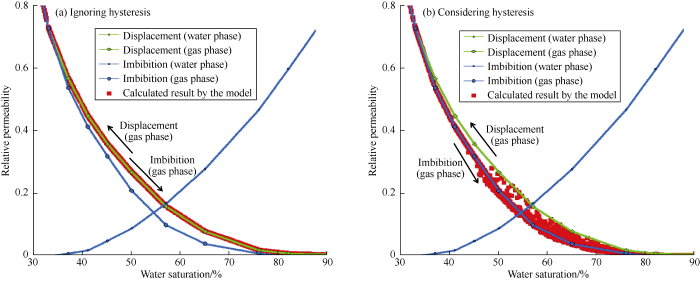
The relative permeability envelopes in our study were obtained using lab tests of alternating gas-water displacement. Relative permeability hysteresis of water phase in the tests was not significant, the water phase displacement envelope was set to coincide with the imbibition envelope during the calculation. Relative permeability hysteresis has a great impact on simulation results (Fig. 5). Relative-permeability points of gas phase (red dots in the figure) lie on the displacement envelope if relative permeability hysteresis is not considered from numerical simulations, while the data points fall between the imbibition envelope and displacement envelope if relative permeability hysteresis is involved.
Fig. 5.
Fig. 5.
Relative permeability curves used in the numerical simulation model.
Fig. 6.
Fig. 6.
Permeability distribution in the 3D geologic model.
Fig. 7.
Fig. 7.
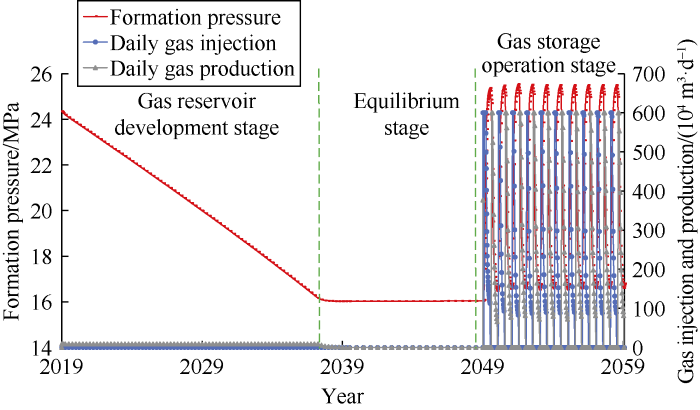
Simulated pressure and daily gas injection and production at different stages.
2.2. Numerical model
The parameters in Table 1 were used to build the 3D geologic model to investigate relative permeability hysteresis in multi-cycle injection and production (Fig. 6). The model, which consists of 124×104 grids, was designed with subdued structure. The gravity has a small impact on fluid distribution in it. The reservoirs had planar heterogeneity, local dominant channels, and low-permeability barriers between layers. The model also consists of edge water and bottom water system and analytic water at the boundary. The initial state was defined with a uniform gas-water contact.
Table 1 3D geologic model parameters.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Grid spacing along the X-axis | 10 m | Average permeability along the Z-axis | 1.23×10-3 μm2 |
| Grid spacing along the Y-axis | 10 m | Average permeability in gas-bearing area | 19.00×10-3 μm2 |
| Grid spacing along the Z-axis | 2 m | Initial formation pressure | 24.35 MPa |
| Number of grids along the X-axis | 200 | Elevation of gas-water contact | -2475 m |
| Number of grids along the Y-axis | 200 | Average reservoir thickness | 35 m |
| Number of grids along the Z-axis | 31 | Geologic reserves | 10.28×108 m3 |
| Area of structure | 4 km2 | Pore volume containing gas | 467.69×104 m3 |
| Elevation of structure top | -2435 m | Grid-water pore volume | 3180×104 m3 |
| Maximum dip angle | 10° | Gas density | 0.81 kg/m3 |
| Average porosity | 15.25% | Formation water density | 1018 kg/m3 |
| Average permeability along the X-axis | 13.50×10-3 μm2 | Formation water viscosity | 0.397 mPa•s |
| Average permeability along the Y-axis | 13.50×10-3 μm2 | Formation water compressibility | 3.97×10-6/MPa-1 |
3. Numerical simulation
3.1. Design
The whole process from gas reservoir development to underground gas storage operation was designed with several stages: gas reservoir development, equilibrium, and gas storage operation (Fig. 7).
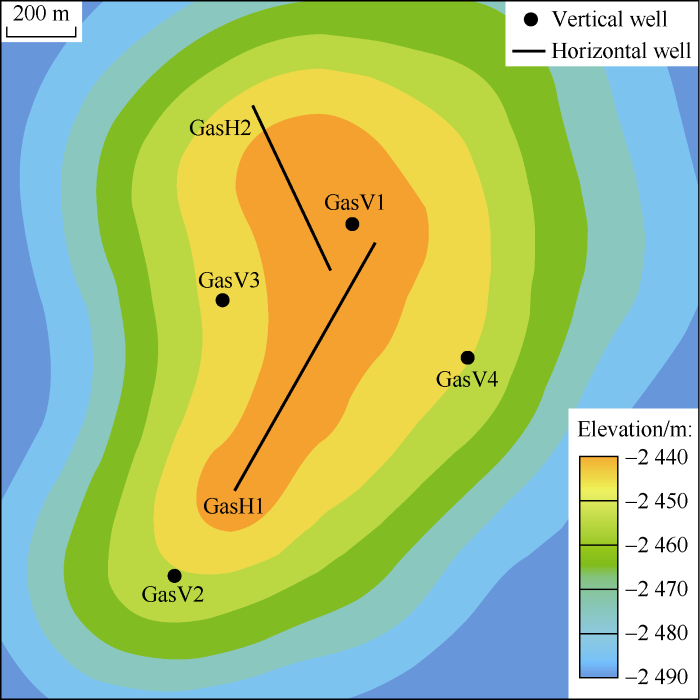
A vertical well and a horizontal well were deployed at the stage of gas reservoir development (GasV1 and GasH1). The reservoir was set to develop at an annual rate of 2.5% (of geologic reserves) for 20 years, terminate at remaining geologic reserves of 50% for gas storage, and shut down wells for 10 years to realize fluid equilibrium. Additional 3 vertical wells and 1 horizontal well were deployed at the stage of gas storage operation (Fig. 8) to realize overall control of the well network on the gas-bearing area. The new vertical wells lie at the margin and flank of the gas-bearing area, and the lowest horizon for well completion was 10 m from the initial gas-water contact. The horizontal section was 30 m from the initial gas-water contact.
Fig. 8.
Fig. 8.
Well-site deployment in the gas storage.
Dynamic parameters of each gas well in the geologic model were adjusted in accordance with simulated short-term individual-well injection and production tests. The maximum individual-well gas injection and production capacities were properly set, the maximum bottom-hole flowing pressure during gas injection and production was controlled, and the total gas injection and production volumes in the whole gas storage were determined using optimized well-group proration production (Table 2). Three schemes, i.e., Carlson, Killough hysteresis correction, and the one ignoring hysteresis, were designed with two scenarios, viz. constant flowing-pressure production and constant gas-volume production. Ten cycles were set for the gas storage with injection followed by production to build up formation pressure.
Table 2 Constraints for the gas storage during injection and production.
| Well number | Maximum individual-well gas injection/production volume/(104 m3·d-1) | Well-group gas injection/production volume/(104 m3·d-1) | Bottom-hole flowing pressure limit in gas production/MPa | Flowing pressure limit in gas injection/MPa |
|---|---|---|---|---|
| GasH1 | 200 | 600 | 16 | 26 |
| GasH2 | 200 | |||
| GasV1 | 120 | |||
| GasV2 | 70 | |||
| GasV3 | 70 | |||
| GasV4 | 70 |
3.2. Influence of relative permeability hysteresis on
gas-water distribution in the gas storage
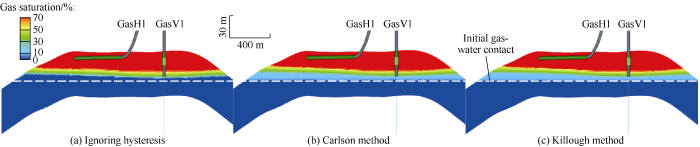
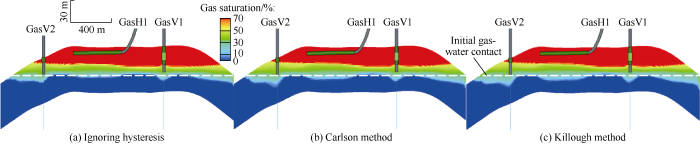
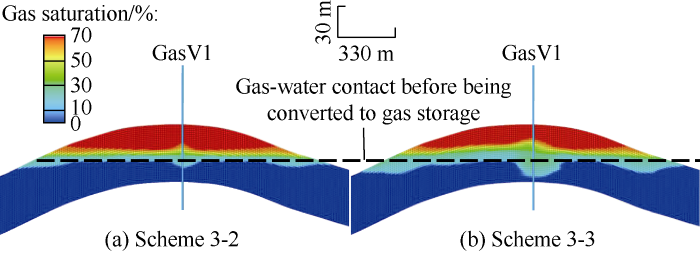
Compared with gas saturation distribution before building the gas storage, the simulation not considering relative permeability hysteresis effect showed that the gas-water contact rose gently vertically (Fig. 9a) at the stage of low-speed gas reservoir development; the simulations by the two methods considering relative permeability hysteresis effect showed that the gas-water transition zone had the lower margins basically consistent with the initial gas-water contact before development, but increasing significantly in thickness (Fig. 9b, c).
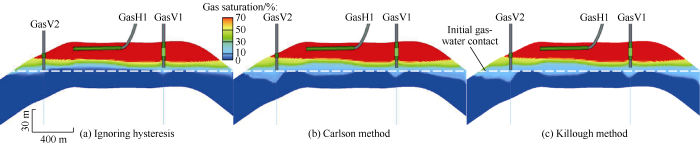
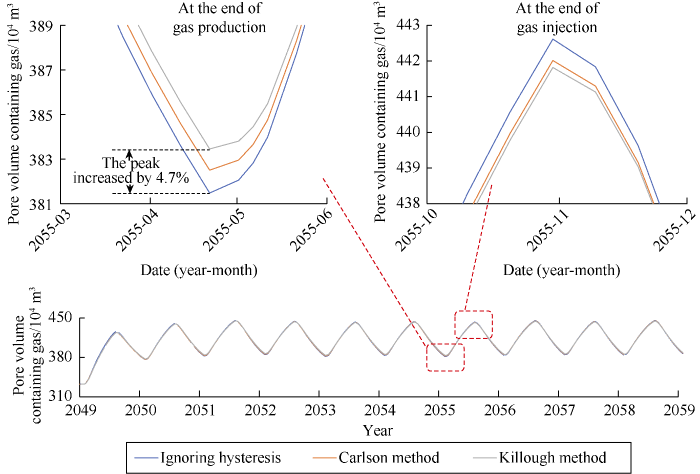
At the stage of gas storage operation, the gas-water transition zone obtained using two methods considering relative permeability hysteresis was 8 m thicker at the end of gas production and 4 m thicker at the end of gas injection compared with the results obtained without hysteresis effect, and the gas cap decreased by 2 m in thickness on average (Figs. 10 and 11). Laterally, the gas-water transition zone was 80 m wider at the end of gas production and 60 m wider at the end of gas injection; the major and minor axes of the gas cap decreased by 120 m on the average (Fig. 12). The peak of pore volume containing gas decreased in variation magnitude with multi-cycle injection and production, and increased by 4.7% on the average at the end of gas production in Killough scheme (Fig. 13), and the recoverable gas volume decreased accordingly. This indicates that water invasion intensified at the stage of gas production; at the following
Fig. 9.
Fig. 9.
Gas saturation distribution before gas storage.
Fig. 10.
Fig. 10.
Gas saturation distribution at the end of gas injection in the 10th cycle.
Fig. 11.
Fig. 11.
Gas saturation distribution at the end of gas production in the 10th cycle.
Fig. 12.
Fig. 12.
Gas saturation distribution in the middle of the reservoir at the end of gas production in the 10th cycle.
Fig. 13.
Fig. 13.
Comparison of pore volumes containing gas from the three schemes.
Fig. 14.
Fig. 14.
Fluid-zone section at the 10th cycle of the gas storage operation.
stage of gas injection, part of gas moved below the initial gas-water contact through dominant channels. Thus, the gas-water transition zone became wider and thicker, and available pore space decreased.
In accordance with above study, the gas storage could be divided into three dynamic fluid zones vertically, viz. high-efficiency gas storage zone, gas-water transition zone, and water zone, the boundaries of which may vary with multi- cycle gas injection and production. According to the results derived from the Killough model in the 10th cycle with the widest gas-water transition zone, the gas saturation section was partitioned through well GasV1 (Fig. 14). Three grids, i.e., P1 at the boundary of the high-efficiency gas storage zone, P2 at the boundary of median gas saturation, and P3 at the boundary of the water zone, were taken as study objects.
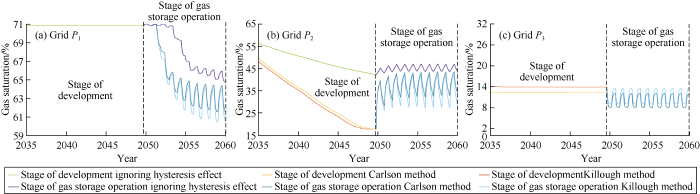
At grid P1, gas saturation calculated by the schemes considering hysteresis (Fig. 15a) decreased at the second cycle of injection and production. Larger amplitude of gas saturation and significant decline indicating that this zone had water invasion and significant hysteresis effect with the injection and production, and more and more gas in this grid flew difficultly in the process of injection and production. With the injection and production going on, the gas saturation at the boundary of the high-efficiency gas storage zone decreased constantly, indicating the high-efficiency gas storage zone did not reach equilibrium and shrank constantly under the current operating conditions. The scheme considering relative permeability hysteresis showed even faster shrink of the high-efficiency gas storage zone.
Fig. 15.
Fig. 15.
Gas saturation curves at grids P1, P2, and P3 simulated by several schemes.
The grid P2 200 m away from well GasV1 had overall stable variations of gas saturation during the gas storage operation stage, and periodic gas saturation fluctuations with the injection and production cycle (Fig. 15b). The simulation of the scheme considering hysteresis showed larger fluctuations of gas saturation at this point. The periodic fluctuations of gas saturation indicate alternating gas-water displacement in this area during the process of gas storage operation. When the shrunk part of the high-efficiency gas storage zone changed into gas-water transition zone, the storage capacity would reduce and the gas-water transition zone could be partially utilized. The gas-water transition zone should be optimized as a buffer zone in the scheme to preserve the high-efficiency storage space in the upper part.
With respect to grid P3, the gas was completely displaced by formation water at the end of gas reservoir development when relative permeability hysteresis was ignored. The gas saturation did not change, and the gas-water contact would be above this grid after multi-cycle injection and production. The simulation considering relative permeability hysteresis showed gas saturation at this point was higher than that from the simulation without hysteresis effect (Fig. 15c). This means that part of the gas was captured by formation water, the gas could not be entirely displaced out by water in a limited period of time due to poor flow capacity of gas phase.
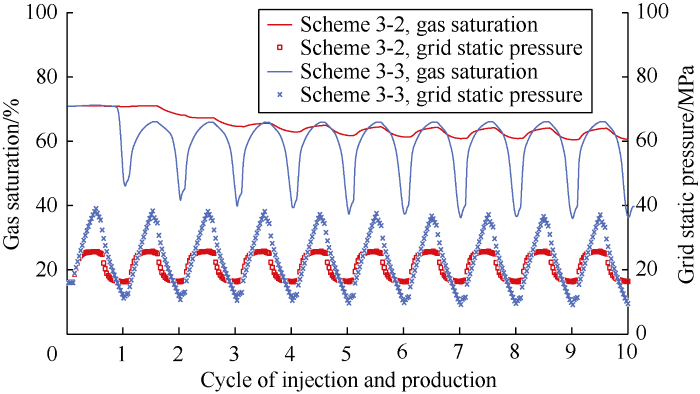
The simulation results of schemes 3-2 and 3-3 in Table 3 (Fig. 16) show gas saturation at grid P1 decreased with the cycle of injection and production. The peak value tended stable after the sixth cycle in scheme 3-2 and the second cycle in scheme 3-3. Gas saturation varied greatly in scheme 3-3; the trough dropped down gradually before the fifth cycle and then tended stable. This indicates that if the pressure difference between injection and production increases, gas sweeping efficiency will improve in the same time, but residual water saturation at the end of gas injection in each cycle cannot be restored to the initial state. Under high injection-production pressure difference, gas would flow along high-permeability channels, resulting in more complicated gas-water transition zone (Fig. 17).
Table 3 Design parameters.
| Scheme | Relative permeability hysteresis | Stage of simulation | Working time/a | Cycle of injection and production | Number of wells | Constraint |
|---|---|---|---|---|---|---|
| 1-1 | No hysteresis | Gas reservoir development | 20 | 2 | Constant production | |
| 1-2 | Gas storage injection and production | 10 | 10 | 6 | Constant pressure and limited gas volume | |
| 1-3 | Constant gas volume | |||||
| 2-1 | Carlson | Gas reservoir development | 20 | 2 | Constant production | |
| 2-2 | Gas storage injection and production | 10 | 10 | 6 | Constant pressure and limited gas volume | |
| 2-3 | Constant gas volume | |||||
| 3-1 | Killough | Gas reservoir development | 20 | 2 | Constant production | |
| 3-2 | Gas storage injection and production | 10 | 10 | 6 | Constant pressure and limited gas volume | |
| 3-3 | Constant gas volume |
Fig. 16.
Fig. 16.
Gas saturation variation with operating pressure at grid P1.
Fig. 17.
Fig. 17.
Comparison of gas-water distribution in different schemes.
The above analysis shows that formation water invading into the high-efficiency gas storage zone cannot be completely displaced out by increasing gas injection pressure difference in the same cycle. In contrast, some injected gas will be lost in the original water zone. In actual gas storage operation, the gas-water transition zone could be controlled through optimizing well deployment and scheme of injection and production to improve the utilization of storage space and extend the life span of the gas storage with high-efficiency injection and production.
3.3. Influence of relative permeability hysteresis on performance indexes prediction
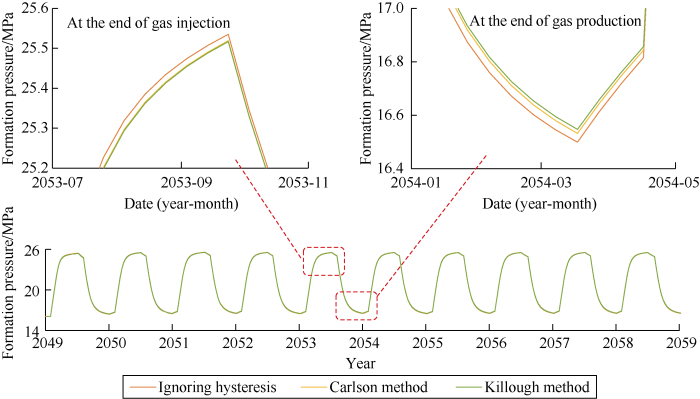
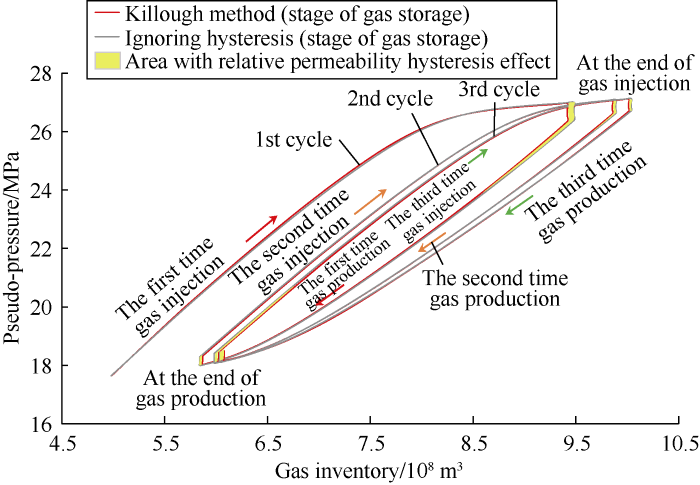
At limited bottom-hole injection-production flowing pressure, the simulation results of schemes considering hysteresis effect yielded lower formation pressure at the end of for gas injection and higher formation pressure at the end of gas production on average compared with the scheme without hysteresis effect (Fig. 18); Multi-cycle storage curves (Fig. 19) showed that the scheme with hysteresis effect increased remaining gas inventory at the end of gas production and decreased gas inventory at the end of gas injection compared with the scheme without hysteresis effect. The working gas volumes simulated by Carlson and Killough methods decreased by 1.2% and 1.8%, respectively.
Fig. 18.
Fig. 18.
Formation pressure variation of the injection-production schemes at constant flowing pressure.
Fig. 19.
Fig. 19.
Gas inventory variation for the injection-production schemes at constant flowing pressure (first 3 injection-production cycles).
It can be seen from the above analysis that: (1) Relative permeability hysteresis effect reduces the flow capacity of gas phase and gas supply volume significantly. Gas producing efficiency drops in the process of gas production, and gas transport capacity becomes poor in the process of gas injection; gas-water transition zone increases in size, movable gas volume decreases, high-efficiency gas storage space reduces, and working gas volume of the gas storage drops. (2) Gas injection at high pressure into aqueous layers tends to cause gas channeling in the area close to the well. During gas production, formation water invades into reservoir rocks and gathers around the area close to the well. Water cone may occur locally in the vertical well, and invaded formation water cannot be completely displaced when gas is injected again and may occupy some pore space. Consequently, the gas-water transition zone expands after multi-cycle alternating injection and production. For the well with completed horizon close to the gas-water transition zone or the well drilled at the margin or flank of the gas storage, individual-well performance indexes will be improperly predicted if relative permeability hysteresis effect is ignored.
4. Case study
An underground gas storage converted from a low-permeability water-invaded gas reservoir is taken to verify our simulation results. The reservoirs in this storage have strong heterogeneity, an average porosity of 10%, average permeability of 2×10-3 μm2, and good connectivity. The reservoir had a uniform gas-water contact before development. Due to local water cones in some producing wells after development, the gas-water contact varied greatly in the lateral direction. The degree of reserve recovery was 40% before the gas reservoir was converted into the gas storage. By far, the gas storage has been successfully put into operation for 6 injection-production cycles.
A 3D geologic model was built for the gas storage and then up-scaled to grid spacing of 100 m×100 m×20 m and grids of 50×70×75. Fluid parameters were derived from laboratory tests on natural cores, and geologic parameters of the model were revised in accordance with full- process history matching from gas reservoir development to gas storage operation.
Comparison of matched curves of performance indexes for well A with completion horizon at the boundary of the gas-water transition zone shows the matched results considering hysteresis effect agree well with observed data. The flow pressures calculated by the two methods considering relative permeability hysteresis are very similar (almost coincide on the figure) (Fig. 20). The water production rate calculated by Killough method is more accurate, indicating the Killough method is more suitable for the model. This means that gas-water distribution and performance indexes after multi-cycle injection and production could be properly predicted if relative permeability hysteresis effect is considered in numerical simulation for the water-invaded gas reservoir-type storage.
Fig. 20.
Fig. 20.
Matched curves of performance data of well A obtained using different methods.
5. Conclusions
Relative permeability hysteresis effect occurs during high-speed injection and production of the underground gas storage converted from a water-invaded gas reservoir. This effect leads to increase of gas-water transition zone width and thickness, shrinkage of the area with high-efficiency gas storage, and decrease of the peak value variation of pore volume containing gas, storage capacity, working gas volume, and life span of high-efficiency operation.
Numerical simulations exhibit large prediction errors of performance indexes if the hysteresis effect is ignored. The Killough and Carlson methods can be used to correct the relative permeability hysteresis effect in water-invaded underground gas storage and improve the prediction accuracy. The Killough method is better adaptable to the example model in this study.
Nomenclature
C—Land constant, dimensionless;
Krgd—relative permeability corresponding to the displacement envelope, dimensionless;
Krgi—relative permeability corresponding to the imbibition envelope, dimensionless;
Sg—gas saturation, %;
Sgc—critical saturation of non-wetting phase in the process of displacement, %;
Sghy—intermediate saturation of non-wetting phase in the process of displacement, %;
Sgi—initial saturation of non-wetting phase, %;
Sgm—maximum saturation of non-wetting phase in the process of displacement, %;
Sgn—normalized gas saturation, %;
Sgt—residual saturation of non-wetting phase at the beginning of imbibition, %;
Sgtm—maximum residual saturation of non-wetting phase in the process of imbibition, %.
Reference
Key technologies and practice for gas field storage facility construction of complex geological conditions in China
Review and prospect of 20 years of underground gas storage in China
Key evaluation techniques in the process of gas reservoir being converted into underground gas storage
Gas-water-rock interactions and factors affecting gas storage capacity during natural gas storage in a low permeability aquifer
Relative permeability hysteresis: Water-alternating-gas injection and gas storage
Relative permeabilities in reservoir simulation
Injection-production mechanisms and key evaluation technologies for underground gas storages rebuilt from gas reservoirs
Inventory forecast in underground gas storage based on modified material balance equation
Laboratory measurements of relative permeability
DOI:10.2118/951047-G URL [Cited within: 1]
Calculation of imbibition relative permeability for two- and three-phase flow from rock properties. Trans. Am. Inst. Min. Metall,
Reservoir simulation with history dependent saturation functions
DOI:10.2118/5106-PA URL [Cited within: 2]
Percolation modeling of relative permeability hysteresis
DOI:10.1016/j.petrol.2014.05.001
URL
[Cited within: 1]

The phenomenon of relative permeability hysteresis is observed during the process of developing an oil field by methods where the flow direction changes and the displacement of oil by water is changed into the displacement of water by oil and vice versa. This paper represents a model of relative permeability hysteresis for drainage and imbibition based on percolation theory. The phenomenon of active oil components' adsorption on the rock-forming minerals is chosen for the main mechanism of hysteresis origin. In the process of drainage, this causes surface hydrophobization of initially hydrophilic rock which leads to each phase relative permeability change. To describe this phenomenon a percolation model for media with microheterogeneous wettability is used. The received numerical solution is represented as relative permeability curves and is qualitatively confirmed by the experimental data. The behavior of relative permeability hysteresis is observed and analyzed for different differential radius distribution curves, capillary network coordination numbers, saturation models and hydrophobization degrees. Further, the introduced methodology can be put into practice for relative permeability calculation considering hysteresis in any porous media to reduce the time spent. (C) 2014 Elsevier B.V.
Hysteresis effects of three-phase relative permeabilities on black-oil reservoir simulation under WAG injection protocols
DOI:10.1016/j.petrol.2019.01.044 URL [Cited within: 1]
An improved approach for estimation of flow and hysteresis parameters applicable to WAG experiments
DOI:10.1016/j.fuel.2017.02.051 URL [Cited within: 1]
SCAL with full hysteresis significantly impact giant carbonate reservoir performance and improve the history match quality case study
Impact of relative permeability hysteresis on geological CO2 storage
Impact of relative permeability hysteresis on the numerical simulation of WAG injection
Mechanism of gas-water flow at pore-level in aquifer gas storage
DOI:10.1007/s11771-013-1888-x
URL
[Cited within: 1]

By means of the pore-level simulation, the characteristics of gas-water flow and gas-water distribution during the alternative displacement of gas and water were observed directly from etched-glass micromodel. The results show that gas-water distribution styles are divided into continuous phase type and separate phase type. The water lock exists in pore and throat during the process of gas-water displacement, and it reduces the gas flow-rate and has some effects on the recovery efficiency during the operation of gas storage. According to the experimental results of aquifer gas storage in X area, the differences in available extent among reservoirs are significant, and the availability of pore space is 33%-45%.
Effect of capillary number and its constituents on two-phase relative permeability curves
DOI:10.2118/12170-PA URL [Cited within: 1]
Verification of a complete pore network simulator of drainage and imbibition