Introduction
Trajectory design is a part of drilling engineering design and an essential basis for trajectory control. An excellent trajectory that meets the drilling purpose is a prerequisite to ensure smoothness of subsequent completion or production and also the key to reducing drilling accidents and improve single-well production. Since the 1950s, with the widespread use of directional well drilling technology, different trajectory design methods have been proposed to support various directional wells[1,2,3,4,5,6,7,8,9,10]. These methods assume that the trajectory in the design section comprises one or several types of mathematical curves in specific shapes, whether the trajectory is two-dimensional or three-dimensional[11]. The advantage of these assumptions is that the mathematical equations of these curves are easy to solve and can meet different design requirements.
The drag and torque acting on a drill string are caused by the normal force between the drill string and the wellbore. Their influences on drilling operation are as follows: (1) difficult trajectory control, (2) excessive hook load leads to sticking or obstruction during tripping, (3) drill string fatigue caused by excessive torque during rotary drilling, (4) low rate of penetration reduce the work efficiency during sliding drilling, and (5) drill string buckling limits the transmission of WOB (weight on bit) and extension of wellbore[12,13]. Reducing the drag and torque on the drill string in a directional well can lower the drilling difficulty of the well. However, the commonly used trajectory types currently such as circular arc with inclined plane[14,15,16], circular helix[17,18], and natural curve[19,20] fail to consider the mechanical characteristics of the drill string, and measures for drag and torque reduction are aimed only at optimization of the parameters of selected well type. Although the catenary trajectory considers the correlation between trajectory geometry and drill string deformation, there is a deviation between the designed trajectory and reality because the stiffness of the drill string is ignored. In addition, the catenary trajectory has few controllable parameters and little room for shape adjustment, making it difficult to meet the requirements[21,22,23].
This paper presents a new trajectory design method— the suspender line trajectory design. This new method takes the centerline of the deformed elastic rod as the trajectory of the main building-up section to effectively reduce the drag and torque of the drill string in a wellbore while meeting the requirements of trajectory design and targeting. Assuming a drill string in the space is only constrained on its two ends, and it hangs naturally under static balance with the effect of its own gravity. If put the drill string into a wellbore with the same shape, it would keep the same curvature with the wellbore trajectory at any position, thus reducing the normal force between the drill string and the well wall and further reducing drag and torque. However, there are several problems with this method: (1) how to establish the suspender line trajectory and what requirements should the trajectory meet; (2) how is the effect of drag and torque reduction of this trajectory compared with conventional trajectories; (3) what advantages does the suspender line trajectory have compared with catenary trajectory, and (4) what situations is the suspender line trajectory suitable for? In view of these questions, the model establishment, drag and torque reduction effect and adaptability of suspender line trajectory design method are discussed in this paper, in the hope to make this method apply in drilling engineering design and able to reduce drag and torque. Meanwhile, the process of suspender line trajectory design is the simulation of the stress and deformation of the drill string, a corresponding mechanical model of drill string needs to be used, which provides a new idea for combining drill string mechanics with trajectory design.
1. Mechanical model of suspender line
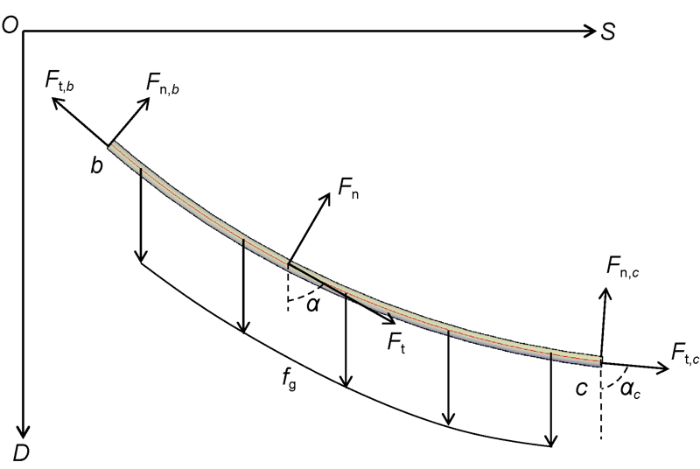
The drill string in a wellbore is in a state of suspension under the action of end tension and buoyant weight and can be regarded as an elastic suspender. The elastic suspender is introduced into the two-dimensional rectangular coordinate system O-SD with node b as initial point and node c as end point (Fig. 1). Regarding the centerline of the elastic suspender as the trajectory between nodes b and c, this well interval is called the suspender section bc, and its length is denoted as Lbc. Thus, the calculation of the stress and deformation of a drill string can be converted into the trajectory design of the suspender section.
Fig. 1.
Fig. 1.
Force analysis of drill string in suspender section.
The design parameters of a point at any arc length s from node b include axial force, shear force, build-up rate, deviation angle, horizontal displacement, and vertical depth. The equilibrium equations of the suspender section can be obtained by simplifying the Kirchhoff equation for the elastic rod[24,25]:
The trajectory of the suspender section can be described[26] as:
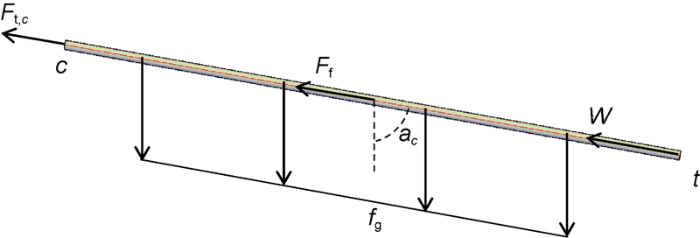
A hold section ct with a length of Lct should be connected to node c (Fig. 2) to ensure that section bc is in a state of suspension. The drill string in the wellbore of section ct must provide enough axial tension which should satisfy the balance equation:
where Ff can be further expressed as:
In Eq. (4), the sign ‘±’ should be ‘+’ when the design aim is to reduce the drag in sliding drilling or tripping in. The sign ‘±’ should be ‘-’ when the design aim is to reduce the drag in tripping out. The friction coefficient μ is equal to zero when the design aim is to reduce the torque in rotary drilling. Since sliding drilling is a dangerous and common operation, this study selects the reduction of drag in sliding drilling as the design purpose of the suspender line trajectory, that is, the sign ‘±’ is ‘+’ in Eq. (4).
Fig. 2.
Fig. 2.
Force analysis of the drill string in hold section along wellbore axis.
According to the property of the hold section trajectory, the relationships between the deviation angle at node c, the length of the hold section and the coordinates at node c and target point t can be obtained:
2. Design method of suspender line trajectory
2.1. Parameters of suspender line trajectory design
The suspender line trajectory comprises a vertical section Oa, a transition section ab, a suspender section bc, and a hold section ct (Fig. 3). The known parameters of the trajectory design are the vertical depth at the kick-off point a, deviation angle at node b, build-up rate of transition section ab, vertical depth and horizontal displacement at target point t, and maximum value of build-up rate of wellbore. The parameters to be determined for the drilling operation are the drill string specifications (outer diameter, inner diameter, elastic modulus, and buoyant weight of unit length of drill string), friction coefficient, weight on bit, and torque on bit in rotary drilling.
2.2. Design of suspender section trajectory
The transition section ab connects with the vertical section Oa and the suspender section bc. It comes into being to provide sufficient deviation at node b, otherwise, the trajectory near node b may be similar to a vertical line or inclined straight line because of the lower initial build-up rate, not conducive to the formation of suspender line trajectory. The transition section ab can be designed as a two-dimensional arc, and its build-up rate can be adjusted according to the requirements. The coordinates of point b, Sb, Db, and well depth Lb can be calculated by the two-dimensional trajectory design method when the vertical depth at node a, deviation angle at node b, and build-up rate of transition section ab are given.
Assuming that the suspender section is composed of m units and m+1 nodes, and the length of each unit is denoted as ΔL, the total length of section bc can be expressed as:
Fig. 3.
Fig. 3.
Composition of suspender line trajectory.
From the above discussion, any point in section bc has these parameters Ft, Fn, k, α, S, and D. These parameters can be represented at nodes, with node i as an example, and the above parameters are denoted as Ft,i, Fn,i, ki, αi, Si, and Di. Thus, Eqs. (1) and (2) can be rewritten as node parameters using linear interpolation as:
Eq. (8) is a set of discrete equations for calculating the trajectory of the suspender section and has 6m equations and 6(m+1) node parameters. Six known parameters or constraint equations must be found at nodes b and c as boundary conditions to make the Eq. (8) close. Besides αb, Sb, and Db, the build-up rate kb at node b is a controllable parameter and can adjust the suspender line section at build-up rate not exceeding the maximum. In addition, there are two constraint equations composed of node parameters at node c, Eqs. (3) and (5). Then, the boundary conditions of the suspender section can be obtained as:
Introducing Eq. (9) into Eq. (8) to make the equations close[27]. The parameters ki, αi, Si, and Di at any node can be obtained using a numerical method. Moreover, the length of the unit can be adjusted to ensure that the build-up rate at each node is less than the maximum build-up rate of wellbore.
After working out the parameters αc, Sc, and Dc at point c and the section length Lbc, deviation angle αt and well depth Lt at target point t and length of section Lct can be obtained by the inclined straight trajectory design method. So far, the deviation angle, build-up rate, vertical depth, horizontal displacement and well depth at key nodes a, b, c, and t have been determined. Except the suspender line section, the parameters of nodes in other sections can be obtained by using the directional well interpolation method[28].
3. Comparison and analysis
3.1. Trajectory design
To analyze the effect of the suspender line trajectory in reducing drag and torque, parameters of suspender trajectory design and drilling operation need to be set and then a series of trajectory data needs to be calculated. Taking one set of calculation as an example, the design and drilling parameters of the suspender line trajectory in this calculation are shown in Tables 1 and 2, and the calculated data of the suspender line trajectory are shown in Table 3. The 4 sections of the trajectory, LOa, Lab, Lbc and Lct are 600, 75, 1199.08, and 4794.23 m long respectively. The deviation angle at target point t is 66.3°.
Table 1 Parameters of trajectory design.
| Parameter | Sign | Value |
|---|---|---|
| Wellhead coordinates | SO | 0 m |
| DO | 0 m | |
| Target point coordinates | St | 5000 m |
| Dt | 3600 m | |
| Vertical depth of kick-off point a | Da | 600 m |
| Deviation angle at node b | αb | 15° |
| Build-up rate at node b | kb | 6°/30 m |
| Build-up rate of transition section ab | kab | 6°/30 m |
| Maximum build-up rate | kmax | 6°/30 m |
Table 2 Parameters of drilling operation.
| Parameter | Sign | Value |
|---|---|---|
| Outer diameter of drill string | Od | 127 mm |
| Inner diameter of drill string | Oi | 101 mm |
| Elastic modulus | E | 2.14×1011 Pa |
| Buoyant weight of drill string | fg | 240 N/m |
| Friction coefficient | μ | 0.25 |
| WOB | W | 100 kN |
| Torque on bit in rotary drilling | T | 3000 N·m |
Table 3 Design results of suspender line trajectory.
| Section | Well depth/m | Deviation angle/(°) | Vertical depth/m | Horizontal displacement/m | Build-up rate/((°)·(30 m)-1) |
|---|---|---|---|---|---|
| Vertical section | 0 | 0 | 0 | 0 | 0 |
| 300.00 | 0 | 300.00 | 0 | 0 | |
| 600.00 | 0 | 600.00 | 0 | 0 | |
| Transition section | 600.00 | 0 | 600.00 | 0 | 0 |
| 615.00 | 3.00 | 614.99 | 0.39 | 6.00 | |
| 630.00 | 6.00 | 629.95 | 1.57 | 6.00 | |
| 645.00 | 9.00 | 644.82 | 3.53 | 6.00 | |
| 660.00 | 12.00 | 659.56 | 6.26 | 6.00 | |
| 675.00 | 15.00 | 674.15 | 9.76 | 6.00 | |
| Suspender line section | 675.00 | 15.00 | 674.15 | 9.76 | 6.00 |
| 680.00 | 15.25 | 678.98 | 11.03 | 3.75 | |
| 780.00 | 16.61 | 775.10 | 38.60 | 0.36 | |
| 880.00 | 17.95 | 870.60 | 68.28 | 0.42 | |
| 980.00 | 19.53 | 965.30 | 100.38 | 0.51 | |
| 1080.00 | 21.39 | 1059.01 | 135.29 | 0.60 | |
| 1180.00 | 23.63 | 1150.40 | 173.51 | 0.75 | |
| 1280.00 | 26.34 | 1242.07 | 215.68 | 0.87 | |
| 1380.00 | 29.71 | 1330.38 | 262.56 | 1.11 | |
| 1480.00 | 33.94 | 1415.41 | 315.16 | 1.41 | |
| 1580.00 | 39.36 | 1495.73 | 374.67 | 1.83 | |
| 1680.00 | 46.39 | 1569.10 | 442.46 | 2.37 | |
| 1780.00 | 55.56 | 1632.32 | 519.85 | 3.12 | |
| 1860.00 | 64.70 | 1672.29 | 589.05 | 3.69 | |
| 1870.00 | 65.88 | 1676.47 | 598.13 | 3.54 | |
| 1874.08 | 66.30 | 1672.97 | 610.46 | 0.37 | |
| Hold section | 1874.08 | 66.30 | 1672.97 | 610.46 | 0.37 |
| 2880.00 | 66.30 | 2077.30 | 1531.55 | 0 | |
| 3880.00 | 66.30 | 2479.25 | 2447.21 | 0 | |
| 4880.00 | 66.30 | 2881.19 | 3362.87 | 0 | |
| 5880.00 | 66.30 | 3283.14 | 4278.53 | 0 | |
| 6380.00 | 66.30 | 3484.12 | 4736.36 | 0 | |
| 6668.31 | 66.30 | 3600.00 | 5000.36 | 0 |
Table 4 Orthogonal experimental scheme of drag and torque reduction rates.
| No | αb/(°) | kb/((°)·(30 m)-1) | W/kN | μ | Sat/m | Dat/m |
|---|---|---|---|---|---|---|
| 1 | 12 | 0 | 50 | 0.15 | 4000 | 4000 |
| 2 | 12 | 0 | 75 | 0.25 | 6000 | 6000 |
| 3 | 12 | 3 | 50 | 0.35 | 6000 | 5000 |
| 4 | 12 | 3 | 100 | 0.15 | 5000 | 6000 |
| 5 | 12 | 6 | 75 | 0.35 | 5000 | 4000 |
| 6 | 12 | 6 | 100 | 0.25 | 4000 | 5000 |
| 7 | 15 | 0 | 50 | 0.35 | 5000 | 6000 |
| 8 | 15 | 0 | 100 | 0.15 | 6000 | 5000 |
| 9 | 15 | 3 | 75 | 0.25 | 5000 | 5000 |
| 10 | 15 | 3 | 100 | 0.35 | 4000 | 4000 |
| 11 | 15 | 6 | 50 | 0.25 | 6000 | 4000 |
| 12 | 15 | 6 | 75 | 0.15 | 4000 | 6000 |
| 13 | 18 | 0 | 75 | 0.35 | 4000 | 5000 |
| 14 | 18 | 0 | 100 | 0.25 | 5000 | 4000 |
| 15 | 18 | 3 | 50 | 0.25 | 4000 | 6000 |
| 16 | 18 | 3 | 75 | 0.15 | 6000 | 4000 |
| 17 | 18 | 6 | 50 | 0.15 | 5000 | 5000 |
| 18 | 18 | 6 | 100 | 0.35 | 6000 | 6000 |
3.2. Comparison with conventional trajectory
A drill string was placed into the wellbore with the designed suspender line trajectory, and the drag on the drill string during tripping in, tripping out, and sliding drilling and the torque on the drill string during rotary drilling were calculated with the established mechanical model. Meanwhile, a conventional trajectory composed of vertical, build-up, and hold sections was designed based on the same trajectory design and drilling parameters, and the drag and torque of the drill string in the wellbore of this trajectory were calculated. Finally, the effects of drag and torque reduction of the suspender line trajectory were compared and analyzed.
It can be seen from Fig. 4 that the suspender line trajectory has significant reduction in the drag and torque in the four types of drilling operations compared with the conventional trajectory. The suspender line trajectory can be taken as a new type of directional trajectory when reduction of drilling risk or improvement of wellbore extension is the objective. But it must be noted that the suspender line trajectory cannot reduce drag and torque under all conditions; the analysis of its suitable conditions will be discussed later.
Fig. 4.
Fig. 4.
Comparison of drags and torques of two trajectories in four kinds of drilling operations.
Generally, the dangerous operations of a directional well are sliding drilling and rotary drilling. To find out
the degree of drag reduction in sliding drilling and torque reduction in rotary drilling of the suspender line trajectory compared with the conventional trajectory, the drag and torque reduction rates were introduced as evaluation indexes for drag and torque reduction effects and are expressed as:
From Eqs. (10) and (11), the greater the values of εs and εr, the better the drag and torque reduction effect and applicability of the suspender line trajectory are. In this calculation, εs = 18.48% and εr = 16.22%.
3.3. Comparison with catenary trajectory
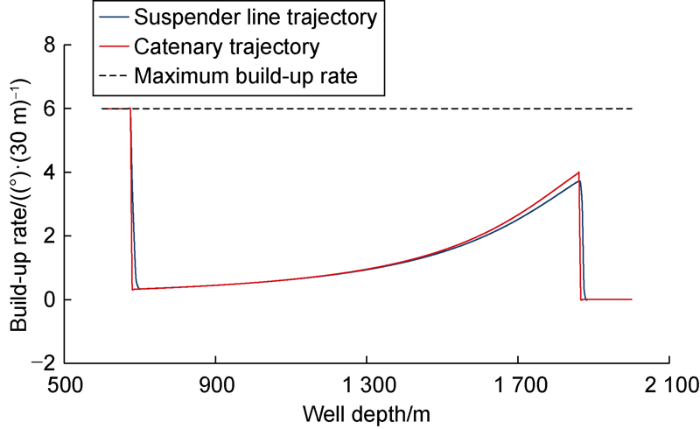
To compare the suspender line trajectory and the catenary trajectory, trajectory of suspender section between nodes b and c was designed by the catenary trajectory method. The deviation angles at nodes b and c were consistent with the results of the suspender line trajectory in Table 3, αb = 15.0° and αc = 66.3°. Then, the build-up rate and the variation of build-up rate with well depth were calculated with the two types of trajectory design methods as shown in Fig. 5 and Fig. 6.
Fig. 5.
Fig. 5.
Variation of build-up rate with well depth of the two kinds of trajectories.
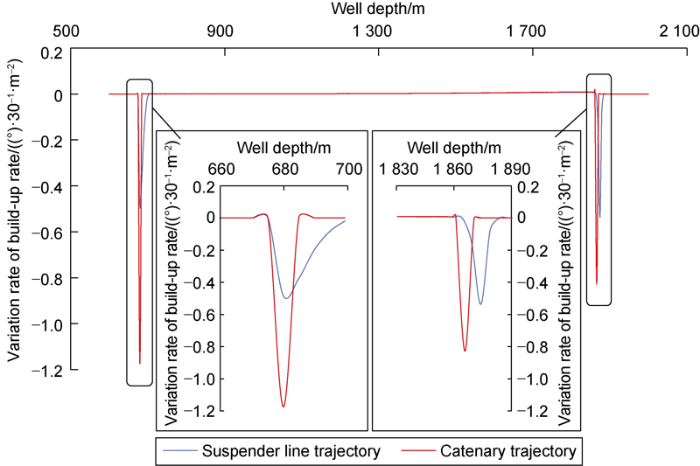
Fig. 6.
Fig. 6.
Variation rate of build-up rate changing with well depth of the two kinds of trajectories.
It can be seen from Fig. 5 that the build-up rates of both the catenary trajectory and suspender line trajectory change exponentially with the increase of the well depth from the initial point, node b (Lb = 675 m). The build-up rates of the catenary trajectory change abruptly at nodes b and c, while the build-up rate of the suspender line trajectory has a narrower decline section. Although both the two types of trajectories have sharp increase of build-up rate near nodes b and c (Fig. 6), the build-up rate of catenary trajectory has much larger variation amplitude than that of the suspender line trajectory. This is because of the nature of catenary trajectory. After αb is given, the shape of catenary trajectory in space is determined, and can’t be optimized by adjusting other parameters at nodes b and c. In comparison, the suspender line trajectory has more controllable parameters than catenary trajectory, and its build-up rates near nodes b and c can be adjusted by Lbc and kb. It can be known from Eq. (1) the variation in the build-up rate would lead to variation of shear force on the drill string and the drill string with unbalanced shear force needs the support of well wall, thus giving rise to normal force between the drill string and the wellbore. Therefore, the normal force would increase sharply at the points with sharp increase of build-up rate, eventually leading to increase in drag and torque on the drill string. It can be seen that, compared with the catenary trajectory, the suspender line trajectory has better adjustability and can slow down the increase in the rate of change of build-up rate caused by the change of track type near the node, thereby reducing the friction and torque at the node of the drill string.
4. Analysis on main factors controlling drag and torque of suspender line trajectory
The suspender line trajectory can reduce the drag and torque on drill string compared with the conventional well trajectory and can be used to reduce drilling risk or increase wellbore extension. If suspender line trajectory is applied in actual drilling, under what conditions it can reduce drag and torque and what degree its drag and torque reduction is need to be studied further. However, trajectory design and drilling operation parameters have different influences on the drag and torque on drill string in the suspender line trajectory. To analyze suitable conditions and the degree of drag and torque reduction of suspender line trajectory, the effects of these parameters on the drag and torque need to be investigated.
The steps for analyzing suitable conditions and degree of drag and torque reduction of the suspender line trajectory in this work were as follows: the drag and torque in the conventional trajectory and suspender line trajectory under the same conditions were calculated first, and then the drag and torque reduction rates compared to the conventional trajectory were taken as the evaluation criteria to evaluate the suspender line trajectory. Namely, the greater the reduction rate, the better the suitability of the suspender line trajectory is. In the description of the new trajectory design method above, the parameters affecting the shape of the suspender section are as follows: (1) the deviation angle, horizontal displacement, vertical depth, and build-up rate at the initial point (node b), (2) the horizontal displacement and vertical depth at target point t, and (3) the friction coefficient and WOB. Obviously, these parameters also affect drag and torque reduction of suspender line trajectory to different degrees and in different ways. The dominant parameters can be selected through screening of main control factors, and then taken as main research objects in the single-factor analysis. In addition, the selection of these parameters depends on the actual drilling operations:
(1) The smoothness of the suspender line trajectory may be decreased because of the instability of the drilling azimuth when the deviation angle αb is too small, while the suspender line section would be smaller in length and lower in the drag and torque reduction capacity if αb is too large. Thus, the value range of αb was taken as 12°-18°.
(2) A larger build-up rate kab should be used to ensure that the deviation angle reaches a predetermined value to reduce the proportion of the non-suspender section in the overall trajectory length. Thus, the build-up rate kab was set at kmax. In consideration of the build-up capacity of ordinary drilling assembly, the kmax was set at 6°/30 m.
(3) The build-up rate kb can be selected arbitrarily without exceeding kmax, and the range of kb is 0-6°/30 m.
(4) Considering that a variation in αb would make the coordinates at node b change and different wells may have kick-off points at different depths, the horizontal distance and vertical distance between the kick-off point a and the target point t were used as parameters to measure the position of the target point in the suspender line trajectory. Generally, directional wells have vertical depth and horizontal displacement both less than 6000 m. In addition, to avoid the failure of suspender line trajectory design because of too large difference between Sat and Dat, Sat and Dat were set both at 4000-6000 m.
(5) The friction coefficients between drill string and wellbore range generally between 0.15 and 0.35. Considering the wide application of PDC (polycrystalline diamond compact) in directional wells, the WOB on this type of bit cannot be too large in sliding drilling, and the WOB was set at 50-100 kN.
According to the ranges of the above parameters, orthogonal experimental schemes shown in Table 4 were made to calculate the drags and torques under different parameter combinations, and then drag reduction rates in sliding drilling and torque reduction rates in rotary drilling of the suspender line trajectory were worked out, respectively (Table 5).
Table 5 Results of orthogonal experimental scheme.
| No | Fc/kN | Fo/kN | εs/% | Tc/(N·m) | To/(N·m) | εr/% |
|---|---|---|---|---|---|---|
| 1 | 93.8 | 200.2 | 53.14 | 16 781.1 | 27 116.4 | 38.11 |
| 2 | 298.8 | 518.9 | 42.42 | 41 076.8 | 63 922.2 | 35.74 |
| 3 | 495.0 | 663.5 | 25.40 | 63 645.4 | 85 429.2 | 25.50 |
| 4 | 112.9 | 259.9 | 56.56 | 20 026.7 | 34 131.2 | 41.32 |
| 5 | 398.2 | 529.5 | 24.80 | 54 498.6 | 69 605.1 | 21.70 |
| 6 | 190.3 | 354.5 | 46.32 | 27 775.4 | 44 292.8 | 37.29 |
| 7 | 382.0 | 623.8 | 38.76 | 50 460.0 | 76 733.9 | 34.24 |
| 8 | 159.4 | 288.5 | 44.75 | 24 768.1 | 37 733.6 | 34.36 |
| 9 | 255.9 | 427.2 | 40.10 | 35 325.2 | 53 335.8 | 33.77 |
| 10 | 313.1 | 450.2 | 30.45 | 42 813.8 | 58 025.9 | 26.22 |
| 11 | 326.4 | 452.3 | 27.84 | 44 381.6 | 58 480.0 | 24.11 |
| 12 | 100.1 | 212.9 | 52.98 | 17 746.3 | 28 814.1 | 38.41 |
| 13 | 327.3 | 493.5 | 33.68 | 43 013.0 | 61 342.6 | 29.88 |
| 14 | 271.8 | 388.8 | 30.09 | 37 288.6 | 50 067.5 | 25.52 |
| 15 | 231.2 | 377.0 | 38.67 | 31 155.9 | 46 354.0 | 32.79 |
| 16 | 171.0 | 269.9 | 36.64 | 25 634.9 | 35 954.3 | 28.70 |
| 17 | 135.4 | 254.9 | 46.88 | 21 454.2 | 33 467.4 | 35.90 |
| 18 | 486.0 | 698.9 | 30.46 | 63 658.3 | 87 672.1 | 27.39 |
The ranges of drag reduction rate of αb, kb, W, μ, Sat, and Dat in sliding drilling were 5.37, 2.50, 1.34, 17.90, 7.96, and 9.48, respectively, the ranges of torque reduction rate of αb, kb, W, μ, Sat, and Dat in rotary drilling were 3.25, 1.59, 0.65, 8.65, 4.48, and 7.59, respectively. The top four parameters from the largest to the smallest, in order, are μ, Dat, Sat, and αb, indicating they have the largest impact on drag and torque reduction effect of suspender line trajectory and can be regarded as the main factors controlling drag and torque reduction rate. In contrast, kb and W within the set scope have smaller influence on the drag and torque reduction rates.
5. Influence patterns of the main control factors on drag and torque reduction
The μ, Dat, Sat, and αb are the main control factors affecting the drag and torque reduction of the suspender line trajectory. The influence patterns of them were analyzed within the setting ranges to find out the suitable conditions of the suspender line trajectory and corresponding recommendations. In this analysis, the ranges of the main control parameters were set according to actual drilling conditions (Table 6), while the parameters having less influence on the drag and torque reduction of the suspender line trajectory (kb and W) were set at average values of 3°/30 m and 75 kN, respectively.
Table 6 Ranges and step lengths of main factors affecting drag and torque reduction rate.
| Factor | Range | Step length |
|---|---|---|
| μ | 0.15-0.35 | 0.10 |
| Dat | 0-6000 m | 500 m |
| Sat | 0-6000 m | 500 m |
| αb | 12°-18° | 3° |
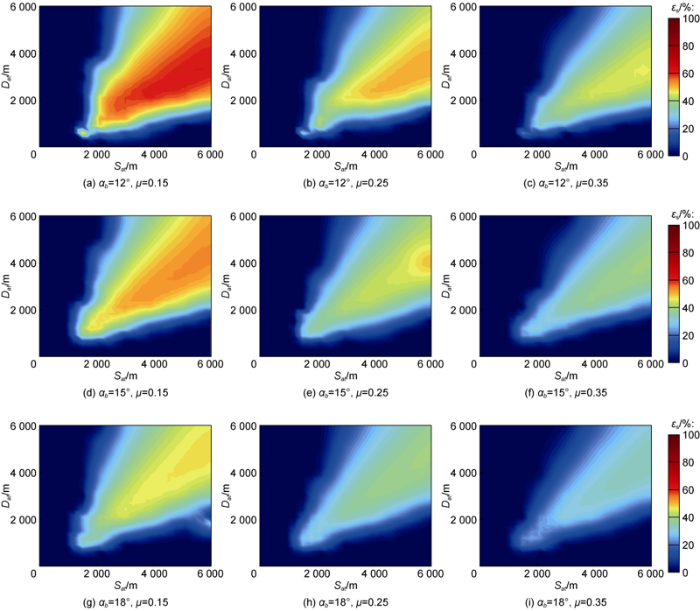
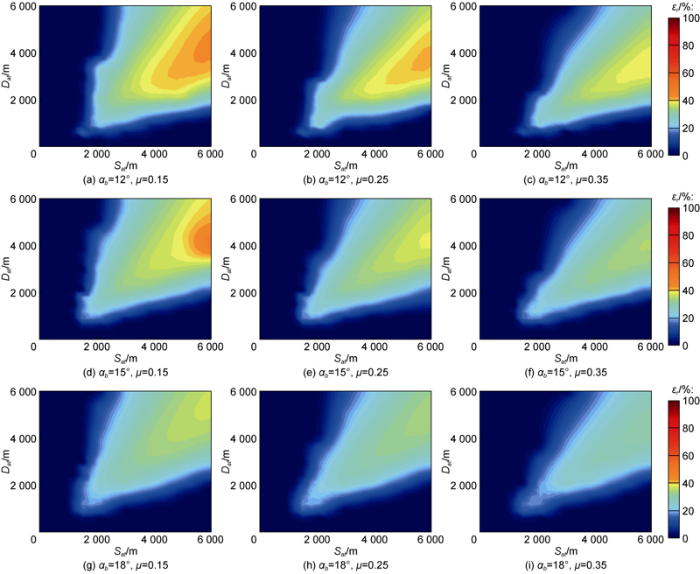
Suspender line trajectories and conventional trajectories were designed under different parameter combinations, and the drags and torques on the drill string in these two types of trajectories were calculated. The drag and torque reduction rates of the suspender line trajec-tory compared with the conventional trajectory were obtained as shown in Figs. 7 and 8. In addition, the drag or torque reduction rate should be equal to 0 when the suspender line trajectory cannot be designed for some parameter combinations; that is, the suspender line trajectory is not applicable in this situation.
Fig. 7.
Fig. 7.
Variation patterns of drag reduction rate with different parameters in sliding drilling.
Fig. 8.
Fig. 8.
Variation patterns of torque reduction rate with different parameters in rotary drilling.
The following conclusions can be obtained by combining the calculations and field applications. The advantage of suspender line trajectory in reducing drag and torque becomes visible only when Sat and Dat reach certain lengths (Sat is greater than 2000 m and Dat is greater than 1000 m). The drag reduction rate and torque reduction rate of suspender line trajectory increase gradually with the increase of Sat and Dat, and the suspender line trajectory has the best effect of reducing drag and torque when the ratio of Sat to Dat is close to 1.5. As shown in Figs. 7a and 8a, at μ = 0.15 and αb = 12°, the drag reduction rate εs and torque reduction rate εr reach the maximum values of 60.22% and 43.08%, respectively, when Sat and Dat are approximately 6000 m and 4000 m, respectively. εs and εr decrease gradually to 0 with the increase or decrease of the ratio of Sat to Dat. It can be concluded that the suspender line trajectory is suitable for extended- reach wells with large horizontal distance Sat, vertical distance Dat, and the ratio of the two close to 1.5. εs and εr decrease with the increase of the friction coefficient μ when the deviation angle αb is fixed. As the friction coefficient has the greatest influence on the drag and torque reduction rate, reducing the friction coefficient as much as possible is the main means of bringing the superiority of drag and torque reduction of the suspender line trajectory into full play. εs and εr decrease with the increase of the deviation angle αb when the friction coefficient μ is fixed. A smaller deviation angle αb should be set in the trajectory design of the transition section; however, αb too small would affect the formation of the suspender section. Thus, the range of αb is recommended at 12°-15°.
6. Conclusions
We have come up with a novel directional well trajectory design method called the suspender line trajectory design method as the commonly used trajectory design methods cannot control drag and friction. In this design method, an elastic rod in the state of static equilibrium of suspension under its own gravity and constrained at its two ends is taken as the research object, the centerline of the deformed elastic rod is taken as the trajectory of the directional well to make the drill string in the wellbore maintains the same curvature with the trajectory at any position to reduce drag and torque on the drill string.
The suspender line trajectory comprises vertical, transition, suspender, and hold sections. It can effectively reduce the drag during tripping in, tripping out, and sliding drilling and the torque during rotary drilling compared with the conventional trajectory in a certain parameter interval. In addition, it has more controllable parameters than the catenary trajectory.
The drag and torque reduction rates decrease with the increase of the friction coefficient and deviation angle at the initial point of the suspender line section. The advantage of suspender line trajectory in reducing drag and torque only becomes significant gradually when the horizontal distance and vertical distance from the kickoff point to the target point reach certain lengths, and the larger the horizontal distance and vertical distance, the better the drag and torque reduction effect of the suspender line trajectory is. The effect of reducing drag and torque reaches the maximum when the ratio of the horizontal distance to vertical distance is close to 1.5, the drag in sliding drilling can reduce by up to 60%, and the torque in rotary drilling can reduce by up to 40%. But the drag and torque reduction rates decrease gradually to zero with the increase or decrease of the ratio of the horizontal distance to vertical distance from 1.5, which means that the suspender line trajectory has no advantage in reducing drag and torque in comparison with the conventional trajectory. It can be concluded that the suspender line trajectory is suitable for extended-reach wells with the ratio of the horizontal to vertical distances of close to 1.5 and the horizontal and vertical distances both greater than 3000 m.
Nomenclature
D—vertical depth at any position of suspender section, m;
Dat—vertical distance from kick-off point to target point, m;
Da, Db, Dc—vertical depths at nodes a, b, and c, m;
Di—vertical depth at node i, m;
DO—vertical depth at wellhead, m;
Dt—vertical depth at target point t, m;
E—elastic modulus of drill string, Pa;
fg—buoyant weight of unit length drill string, N/m;
Fc—drag on drill string in suspender line trajectory, N;
Ff—friction on drill string in hold section, N;
Fn—shear force at any position in suspender section, N;
Fn,b, Fn,c—shear force at nodes b and c, N;
Fn,i—shear force at node i, N;
Fo—drag on drill string in conventional trajectory, N;
Ft—axial force at any position in suspender section, N;
Ft,b, Ft,c—axial forces at nodes b and c, N;
Ft,i—axial force at node i, N;
Hj,i—equations of suspender section;
i—sequence number of nodes in suspender section;
I—inertial moment of drill string section, m4;
j—sequence number of equations in suspender section;
k—build-up rate at any position of suspender section, rad/m;
kab—build-up rate in transition section, rad/m;
kb—build-up rate at node b, rad/m;
ki—build-up rate at node i, rad/m;
kmax—maximum build-up rate, rad/m;
Lab—length of transition section, m;
Lb—well depth at node b, m;
Lbc—length of suspender section, m;
Lct—length of hold section, m;
LOa—length of vertical section, m;
Lt—well depth at target point t, m;
ΔL—length of each unit in the suspender section, m;
m—number of units in suspender section;
Od—outer diameter of drill string, m;
Oi—inner diameter of drill string, m;
Rab—arc radius of transition section, m;
s—arc length between any position in suspender section and node b, m;
S—horizontal displacement at any position of suspender section, m;
Sat—horizontal distance from kickoff point to target point, m;
Sb, Sc—horizontal displacement at nodes b and c, m;
Si—horizontal displacement at node i, m;
SO—horizontal displacement at wellhead, m;
St—horizontal displacement at target point t, m;
T—torque on bit, N·m;
Tc—torque on drill string in suspender line trajectory, N·m;
To—torque on drill string in conventional trajectory, N·m;
W—weight on bit, N;
α—deviation angle at any position of the suspender section, rad;
αb, αc—deviation angles at nodes b and c, rad;
αi—deviation angle at node i, rad;
αt—deviation angle at target point t, rad;
εs—drag reduction rate in sliding drilling, %;
εr—torque reduction rate in rotary drilling, %;
μ—friction coefficient.
Reference
Engineering planning and supervision of directional drilling operations
A comparison of various directional survey models and an approach to model error analysis
DOI:10.2118/3379-PA URL [Cited within: 1]
An improved method for computing directional surveys
DOI:10.2118/1992-PA URL [Cited within: 1]
Directional survey calculation
A systematic approach to well surveying calculations
Directional survey by the circular arc method
DOI:10.2118/99744-PA URL [Cited within: 1]
Borehole trajectory uncertainty and its characterization
A new calculation approach of wellbore separation factor based on the relative position of adjacent wells
Analytic description of spatial-arc wellbore trajectory
Progress of research on drillstring backing pressure effect in complex structure well
Improvement of torque-and-drag modeling in long-reach wells
Description and calculation of the well path with spatial arc model
New control mode for well trajectory on circular arc with inclined planes
Evolution pattern and control mode of well deviation for circular-arc trajectories in space
Calculation method of borehole location in directional wells
Numerical method for deviational survey by cylinder helix method
Natural parameter method accurately calculates well bore trajectory
Numerical approaches of natural curve method in inclination survey
Method of non-dimensional design of cautionary shape profile of directional well
Study on the methods of planning a catenary profile of wellbore trajectory
Three-dimensional catenary profile design method
Modeling and analysis of nonlinear mechanics of a super-thin elastic rod
Analysis of the main factors affecting bottom hole assembly re-entry into main hole in forward drilling of fishbone wells
DOI:10.1016/j.petrol.2020.107018 URL [Cited within: 1]
3D horizontal wellbore trajectory optimization design method in the Fuling shale gas field